基于衍生品投资的DC型养老金计划均衡投资策略*

王佩，陈峥，张玲

1. 广东金融学院经济与贸易学院，广东广州510521

2. 中山大学管理学院，广东广州510275

出生率降低和寿命延长使得大多数国家养老金制度面临着越来越严峻的挑战。Poterba 等［1］和Blake等［2］指出为应对养老金支付危机，保证养老保障体系的可持续性，越来越多国家的养老金模式由确定收益型养老金计划（以下简称DB 型养老金计划）转变为确定缴费型养老金计划（以下简称DC 型养老金计划）。这是因为，DC 型养老金计划的缴费是预先确定的，养老金计划参与者退休后所能领取到的金额取决于积累期内养老金账户的投资收益。相应地，投资风险和长寿风险也从养老金计划的发起人转移到参与者身上。从这个意义上讲，DC 型养老金计划有效的投资管理和风险控制对于参与者维持退休后的生活水平具有重要意义。近20 年来，也出现了大量关于DC 型养老金计划最优投资管理的研究。这些研究按照优化准则可划分为两大类：一类是以期望效用最大化为优化准则，如Battocchio等［3］得到了常数绝对风险厌恶效用（CARA）下DC 型养老金计划的最优投资策略；Cairns 等［4］研究了常数相对风险厌恶效用（CRRA）下DC 型养老金计划的最优投资策略；Chen 等［5］研究了DC 型养老金计划的预期S-型效用最大化问题；另一类采用了均值-方差准则，如Yao 等［6］、Guan 等［7］以及Zhang 等［8］研究了均值-方差准则下DC 型养老金计划的最优投资策略。

上述关于DC 型养老金计划最优投资问题的研究有两个方面值得拓展。一方面，以上文献多采用几何布朗运动模型刻画金融市场中风险资产的价格过程，且风险资产的价格波动为常数或关于时间的确定函数。然而许多实证研究表明股票价格的波动率是随机的而非确定的［9-10］。于是，Gao［11］、Guan 等［12］和邓丽梅等［13］在效用最大化准则下分别利用Constant Elasticity of Variance（CEV）模型、Heston 随机波动率模型和仿射平方根随机模型研究了具有随机波动率的DC型养老金计划的最优投资策略。另一方面，上述文献中均值-方差准则下DC 型养老金计划的最优投资策略是时间不一致的，即在初始时刻得到的最优投资策略在未来时刻不再是最优的。这是因为均值-方差目标函数中的方差项不满足期望迭代性质，Bellman最优性原则不再成立。因此，在均值-方差准则下得到的最优投资策略只在初始时刻是最优的，也称为预先承诺策略。然而，投资策略的时间一致性是理性决策者的基本要求。特别对于投资期限通常为三、四十年的DC 型养老金计划而言，如果投资策略缺乏时间一致性，DC 型养老金计划的投资收益可能会遭受意想不到的损失。DC 型养老金计划的决策者更偏好对每个时间点都是最优的时间一致策略，而不是仅在初始时间最优的预先承诺策略。因此，在Björk 等［14］提出的纳什均衡分析框架下，许多学者试图通过求解扩展的Hamilton-Jacobi-Bellman（HJB）方程系统研究均值-方差准则下DC 型养老金计划的时间一致性投资策略（也称均衡策略）［15-17］。

现有DC型养老金计划时间一致投资策略问题的研究中，风险资产的价格过程一般由几何布朗运动刻画，其瞬时收益率和波动率设定为常数。然而，近年金融市场的现状表明风险资产的波动率会受到政治、经济、突发灾难事件等不确定因素的极大影响，风险资产的波动率是时变而非确定的。在长达几十年的投资期限中考虑波动率随机变化对DC型养老金计划均衡投资策略的影响更贴近金融市场实际，一些学者也开始这方面的探索［18-19］。另外，作为风险对冲的有力工具，衍生品在金融投资实践中已是必备选项。然而DC 型养老金计划投资决策问题还较少考虑此类资产。但是，由于衍生品在对冲金融风险方面的有效性，衍生品的投资已引起了广泛关注。近10 年来，一些学者开始关注含有衍生品的最优投资组合问题［20-22］。根据新加坡交易所2015年1月6日发布报告，2014年证券交易量下降了25%，而衍生品交易量则升至历史新高。过去10年来，养老金投资市场中衍生品的投资也越来越多。2012 年英国国家养老基金协会（NAPF）年度调查显示，57%参与者的养老金计划包含衍生品。此外，2016年全球养老金资产研究报告显示，截至2015 年底，全球七大市场（澳大利亚、加拿大、日本、荷兰、瑞士、英国和美国）的平均全球资产配置比例为44%股票、29%债券、3%现金和24%其他资产，其中其他资产主要为衍生品。衍生品在养老金投资市场上越来越流行，相关研究也正在逐步展开，Zeng等［23］研究了模型不确定下基于衍生品投资的DC型养老金计划的稳健最优投资策略。

基于上述研究进展，本文拟在风险资产波动率随机变化且包含衍生品的金融市场中，研究均值-方差准则下DC 型养老金计划的时间一致投资策略。金融市场中包含一个无风险资产、一支股票和一个衍生品。股票的价格过程服从一个随机波动率模型。在Björk 等［14］提出的纳什均衡分析框架下，通过求解相应扩展的HJB 方程系统，得到有衍生品投资和无衍生品投资情形下DC型养老金计划的均衡投资策略和均衡有效前沿。最后用数值算例分析了随机波动率和风险溢价对均衡有效前沿的影响。本文的主要贡献：（i）在均值-方差准则下构建了具有衍生品投资的DC 型养老金计划投资组合模型；（ii）我们发现，衍生品可以显著提高DC型养老金计划的投资绩效，投资于衍生品、无风险资产和股票的均衡有效前沿远远优于投资于无风险资产和股票的均衡有效前沿，因此衍生品是DC型养老金计划参与者提高投资收益的一种可行工具。

1 模型构建与求解

我们考虑DC 型养老金计划的代表性参与者，于0 时刻开始工作，T ＞0 时刻退休。在工作期间，他领取随机的工资，并连续不断地按照固定比例缴纳工资的一部分到自己的养老金账户。为了维持退休后的生活水平，这个代表性参与者将其养老金账户中的财富投资到金融市场以增加自己养老金账户的金额。假设金融市场无摩擦，不考虑交易成本。

1.1 金融市场

金融市场上存在三种资产：一个无风险资产（现金或银行账户）、一支股票和一个衍生品。无风险资产的价格过程S0(t)满足下面的微分方程

其中r ＞0表示无风险利率。股票的价格过程S(t)服从下面的随机微分方程

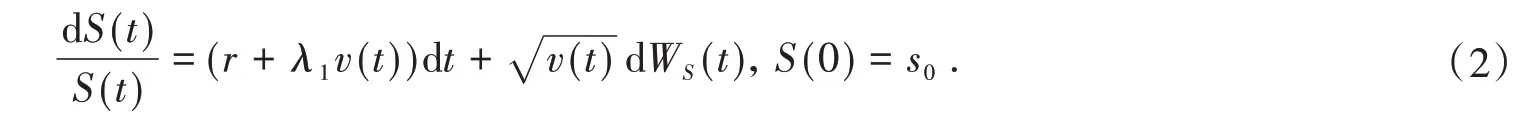
股票收益的方差v(t)满足平方根过程

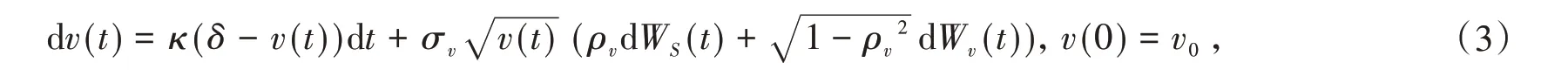
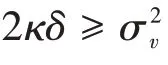
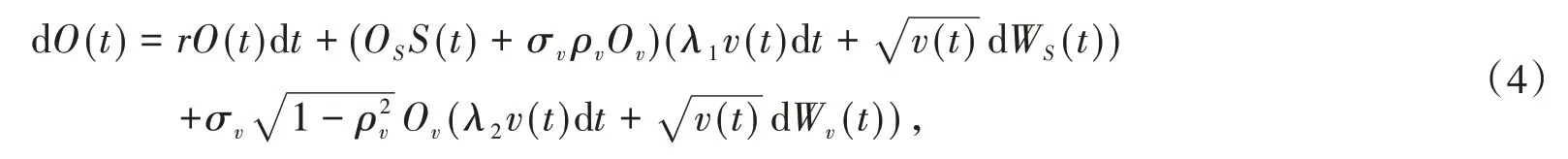
其中OS和Ov分别表示O(t，S(t)，v(t))关于S(t)和v(t)的偏导数，λ2是波动率风险Wv(t)的溢价。

1.2 财富过程

在DC 型养老金计划中，参与者连续不断地向其养老金账户缴纳固定比例ξ（8%或10%）的工资金额。假设参与者的工资L(t)满足下面随机微分方程

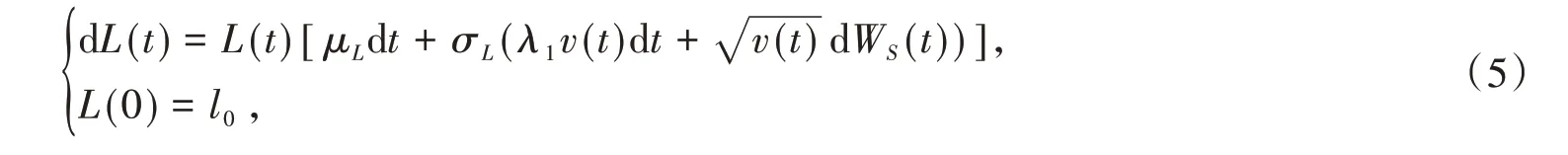
其中μL＞0为工资的预期增长率，σL＞0为工资的波动率。

为了使养老金保值增值，参与者将其养老金账户的财富投资到金融市场。令πS(t)和πO(t)分别表示t时刻投资在股票和衍生品上的财富比例，则1- πS(t) - πO(t)为t 时刻投资于无风险资产中的财富比例。称π：={π(t)：=(πS(t)，πO(t))}t∈[0，T]为一个投资策略，则在投资策略π 下参与者养老金账户的财富Xπ(t)满足如下动态方程

1.3 优化问题与验证定理

1.4 优化问题（8）求解过程

在求解优化问题（8）的均衡策略与相应均衡值函数之前，先化简扩展HJB 方程系统（10）。

命题1扩展HJB 方程系统（10）可简化为

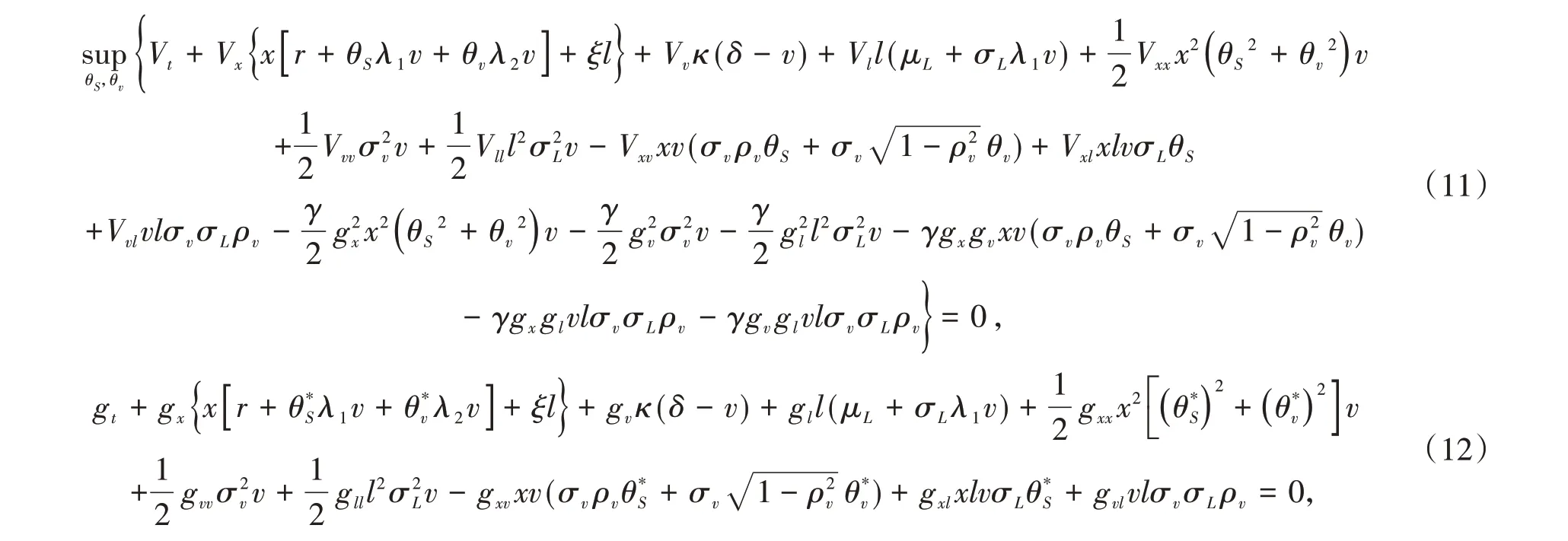
系统（45）～（47）的推导类似于命题1 的证明，此处省略。然后通过类似于定理2 中的推导过程，求解扩展HJB方程系统（45）～（47），即得到（39）～（43）式。证毕

2 敏感性分析

上一节得到了DC型养老金计划的均衡策略和均衡有效前沿，为进一步清晰地展示随机波动率、风险溢价以及衍生品对DC 型养老金计划均衡有效前沿的影响，本节将通过数值分析与数值算例进行直观呈现。参考Zeng 等［23］，模型参数的取值设定为：r = 0.05，κ = 5，δ = 0.132，ξ = 0.2，λ1= 2，λ2= -6，μL=0.08，σL= 0.5，σv= 0.25，γ = 0.5，ρv= -0.4，x0= 4，l0= 1，v0= 0.152，t = 0，T = 20。

总体而言，从图1和图2可明显看出，投资于衍生品、无风险资产和股票情形的均衡有效前沿明显优于只投资无风险资产和股票情形的均衡有效前沿。这意味着在DC型养老金计划投资决策中纳入衍生品可以改善均衡有效前沿、降低DC型养老金计划的投资风险。

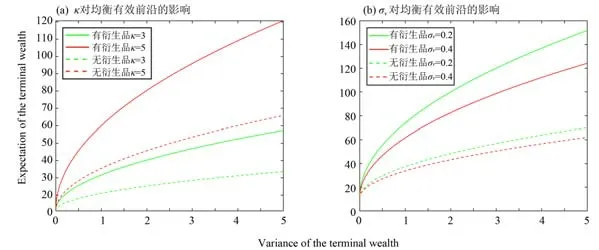
图1 参数κ和σv对均衡有效前沿的影响Fig.1 The effect of parameters κ and σv on the equilibrium efficient frontier

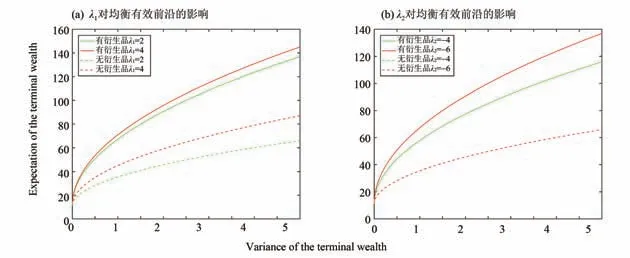
图2 参数λ1和λ2对均衡有效前沿的影响Fig.2 The effect of parameters λ1 and λ2 on the equilibrium efficient frontier

图1 显示了v(t)的均值回复速率κ 和波动率σv对DC 型养老金计划均衡有效前沿的影响。由图1（a）可发现，随着κ 的增长，v(t)的不确定性越小，在退休时财富的期望水平相同时，退休时财富的方差越小，也就是说投资风险降低。与之相反，当σv变大时，v(t)的不确定性增大，当退休时财富的期望水平相同时，退休时财富的方差变大，投资风险升高。

图2 揭示了风险WS(t)的溢价λ1和风险Wv(t)的溢价λ2对均衡有效前沿的影响。我们发现，当方差固定时，对于有衍生品交易情形，均衡有效前沿随着λ1的增大而上升、随着λ2的增大而降低；而对于无衍生品交易情形，均衡有效前沿随λ1的增大而上升，而λ2对均衡有效前沿无影响。由于λ1的值为正，λ2的值为负，我们分析|λ1|和|λ2|对均衡有效前沿的影响。随着λ1增大，退休时财富的方差相同时，退休时财富的期望更大，均衡有效前沿上升。这主要是因为λ1越大，股票的预期收益率越大，这有助于参与者通过承担相同的风险水平而获得更高的收益。|λ2|越大，意味着来自Wv(t)的风险越大，这种风险可以由衍生品对冲，而不能由股票对冲。因此，在无衍生品情形中，λ2的变化对均衡有效前沿没有影响，因此图2（b）中无衍生品情形下，λ1= -4 与λ2= -6 对应的均衡有效前沿重合。相反，来自Wv(t)风险越大，作为对冲工具的衍生品就越有用。因此，|λ2|越大，投资组合的风险减低，从而提升均衡有效前沿。

4 结束语

本文研究了均值-方差准则下可投资衍生品的DC 型养老金计划的均衡投资策略。根据Björk 等［14］提出的博弈论思想，得到优化问题满足的扩展HJB 方程系统。通过求解扩展HJB 方程系统得到均衡投资策略和相应均衡值函数的解析表达式。并进一步得到了无衍生品投资情形的均衡投资策略和相应均衡值函数的解析式。最后，本文分析了随机波动率和风险溢价对均衡有效前沿的影响，投资于衍生品、无风险资产和股票情形的均衡有效前沿明显优于只投资无风险资产和股票情形的均衡有效前沿，说明投资衍生品可以有效地提高投资效率、降低投资组合风险。