基于遗传算法的离心压缩机蜗壳参数化及多目标优化

李 伟，左志涛,3，侯虎灿，梁 奇，林志华，陈海生,3

（1中国科学院工程热物理研究所，北京100190；2中国科学院大学，北京100049；3国家能源大规模物理储能技术(毕节)研发中心，贵州 毕节551712）

压缩空气储能系统是一种能够实现大容量和长时间电能存储的电力储能系统，被认为是最有发展潜力的大规模储能技术之一[1-2]。它通过压缩空气储存多余的电能，在需要时，将高压空气释放通过膨胀机做功发电。随着先进压缩空气储能系统规模的不断扩大，与之配套的压缩机机组性能也越来越重要。离心压缩机由于具有单级压比高、运行工况范围广、结构紧凑、运行平稳等特点，广泛应用于压缩空气储能系统。排气蜗壳作为离心压缩机的重要部件之一，收集来自扩压器的气流并将其输送到出口管道。蜗壳通道的横截面积沿周向不断增加，所以蜗壳的另一作用是进一步将动能转化为势能来提升静压。由于蜗壳进口气流速度较高，需要确保在尽可能小的蜗壳通道内的最小流速，以减小总压损失和提高蜗壳扩压和流动性能。排气蜗壳其完全三维的、湍流的内部流动在非设计工况下会引起蜗壳进口周向压力畸变并沿蜗壳通道周向发展，从而会直接影响上游部件叶轮和扩压器的流动稳定性。目前，国内外学者对离心压缩机排气蜗壳的研究，主要集中在两个方面：一是着重于三维蜗壳流动结构及导致压力损失机理(Ayder[3]、Hagelstein[4]、Tanganelli[5]等)的流动分析；二是着重于叶轮、扩压器与蜗壳之间相互作用，从而研究对叶轮性能影响(Mojaddam[6]、郑新 前[7]、Abdelmadjid[8]等)的 匹配分析。针对蜗壳内部流动的分析主要根据Ayder等[3]提出的影响蜗壳整体性能的五个几何参数(截面面积、截面形状、截面径向位置、蜗壳进口位置、隔舌几何形状)，来进行相关试验和数值研究。

然而，国内外对离心压缩机排气蜗壳参数化、多目标优化以及整级数值模拟的研究较少[9]，离心压缩机蜗壳由于三维的、非对称的几何结构使其优化设计更加复杂和耗时，而采用近似模型和多目标遗传算法相结合的方法可以在保证样本数量足够的条件下有效减少数值计算量。为了避免优化过程中出现不合理的截面形状，本文以某先进压缩空气储能系统用离心压缩机为研究对象，对其切向进口外型蜗壳周向截面进行参数化描述，采用Kriging 近似模型[10]对CFD数值模拟结果进行拟合，使用带精英策略的二代非支配排序多目标遗传算法(nondominated sorting genetic algorithm II，NSGA-II)对近似模型进行循环优化设计，来研究在设计工况下离心压缩机蜗壳截面参数对总压损失系数与静压恢复系数的影响，并对优化结果进行了分析。

1 模型参数化

1.1 蜗壳设计方法

本文研究的某先进压缩空气储能系统用离心压缩机由叶轮、有叶扩压器和排气蜗壳组成，在设计工况下质量流量为34 kg/s，转速为8658.7 r/min，总压比为2.48，叶轮共有13 个叶片，叶轮外径为835 mm，扩压器有11个叶片，有叶扩压器外径为1336 mm，叶片高度为52 mm，蜗壳进口圆周直径为1440 mm，离心压缩机结构如图1所示。

图1 离心压缩机结构Fig.1 Schematic diagram of centrifugal compressor

首先对于该离心压缩机已有的叶轮和有叶扩压器进行排气蜗壳匹配设计，蜗壳采用自由涡旋设计[11]，即气体在蜗壳中的流动，在忽略摩擦力矩情况下，满足动量矩守恒定律cur=const。对于切向进口圆形外蜗壳，其通流截面半径rφ和圆周角φ关系为

式中，E=720°πc4ur4/qV4；φ为气流通道圆周角，(°)；r4为蜗壳进口圆周半径，m；rφ为圆形通流截面半径，m；c4u为蜗壳进口气体圆周速度，m/s；qV4为体积流量，m3/s。一般计算出的面积比实际需要值大，因此在之后蜗壳几何参数化和多目标优化时需对计算截面加以修正。

1.2 模型参数化

采用三维设计软件UG NX 对切向进口外蜗壳进行三维参数化建模。由于蜗壳沿圆周方向各个截面形状相似，可以根据蜗壳各截面面积分布进行相应放缩，因此三维问题就转化为了各个截面上二维参数化问题。为了将蜗壳的截面参数作为优化变量，蜗壳周向8 个二维截面形状分别用由8 个控制点约束的直线-三阶B 样条曲线-直线(Line-Bspline-Line)定义。P1、P2、P3、P4、P5、P6为三阶B 样条曲线的控制点。- ——-MN 的长度等于蜗壳进口宽度，直线段- ——-NP6= - ——-NP1，其长度取决于通流截面半径。B样条曲线第一个和最后一个控制点固定，同时首尾约束切向，保证蜗壳严格切向进口，如图2所示。确定8个截面参数之后，通过扫掠命令完成排气蜗壳的三维几何造型。

图2 蜗壳周向截面几何参数Fig.2 Geometric parameters of circumferential cross section of volute

多目标优化的设计变量选取截面曲线的控制点坐标，为了减少优化变量和提高优化设计方法的普适性，根据初始设计蜗壳8个断面的圆心位置和通流截面半径对这控制点坐标进行无量纲化，定义为

1.3 三阶B样条曲线

利用一个带6 个控制点的三阶B 样条曲线来表示蜗壳通流截面参数，可以用很少的参数提高蜗壳形状的多样性和几何自由度。B样条曲线的数学定义为

式中，0≤t≤1,i=0,1,2,…,m。

称为第i段n次B样条曲线段[12]，这些曲线段的集合称为n次B样条曲线段，其顶点Pk(k=0,1,2,…,m+n)所组成的多边形为B样条曲线的特征多边形。Fk,n(t)为n次B样条曲线基函数，也称B样条曲线分段混合函数，其表达式为

由定义式可知，第i段n次B样条曲线只与n+1个顶点Pk(k=0,1,2,…,n)相关，当改变一个控制顶点时，只会对相邻的n+1段产生影响，不会对整条曲线产生影响。当n=3时，所控制的整条B样条曲线具有二阶几何连续性，因此通过三阶B样条曲线可以很好地控制截面的形状。

2 数值计算方法

2.1 网格生成与计算方法

在本研究中用于数值模型的计算域包括入口段、离心叶轮、有叶扩压器及排气蜗壳四部分，各部分网格如图3所示，其中入口段、离心叶轮及有叶扩压器部分使用ANSYS Turbogrid软件进行全六面体结构化网格划分，蜗壳由于几何结构的复杂性使用ANSYS ICEM 进行固体壁面带边界层的四面体非结构化网格划分。在网格划分过程中，对入口段、叶轮、有叶扩压器及蜗壳的边界层进行加密处理，并对叶轮尾缘、蜗壳隔舌等部位进行局部加密以提高对壁面附近流动信息的有效捕捉。网格生成时充分考虑了所采用的湍流模型对yplus的要求。

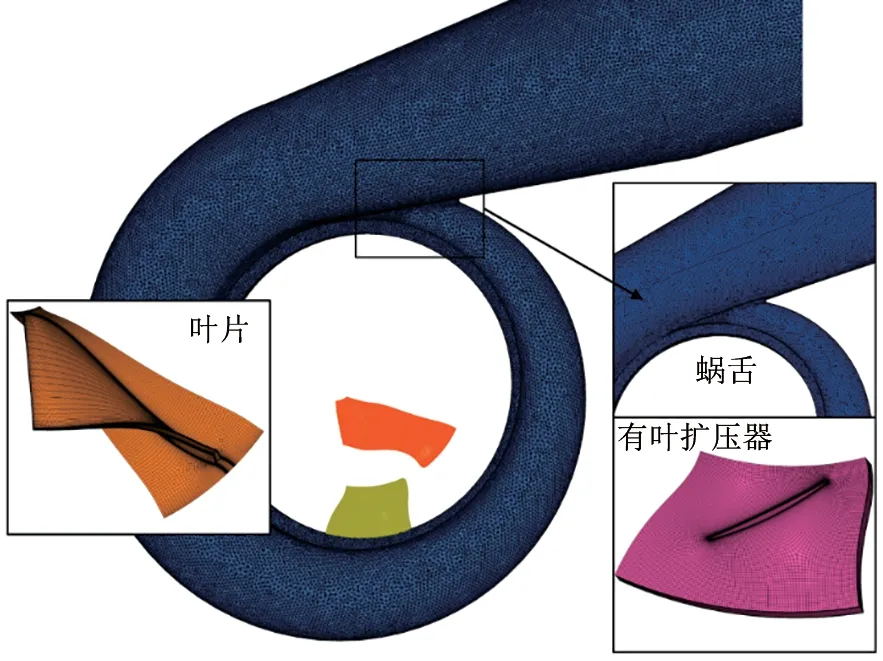
图3 离心压缩机整级网格Fig.3 Grid map of centrifugal compressor

离心压缩机整级三维流场采用商用软件ANSYS CFX 求解定常三维雷诺平均N-S 方程，湍流模型采用k-ε 模型，壁面函数选用Scalable 壁面函数，工作介质为理想气体。叶轮区域为旋转区域，给定压缩机设计转速，其余各部件均为静止区域，采用混合平面法进行动静交界面连接。进口给定总温、总压边界条件，出口给定质量流量边界条件，所有固体壁面给定绝热及无滑移边界条件。计算中叶轮和有叶扩压器区域分别选取一个叶片流道，沿周向给定周期性边界条件。收敛条件设定为最大残差下降至小于1×10−5并趋于稳定，且进出口质量流量的波动在0.5%以内。

考虑到多目标优化的特点及数值计算时间成本，以设计工况的压比和等熵效率作为评价指标，对离心压缩机计算域进行网格无关性验证。首先对入口段、叶轮和有叶扩压器组合进行网格无关性分析，结果如图4(a)所示，随着网格数目的增加，叶轮和扩压器组合效率逐渐稳定，压比变化不明显，因此确定各部分的网格数分别为12 万、127 万、53 万。在选定叶轮和扩压器网格的基础上，对排气蜗壳计算域网格进行无关性验证，验证结果如图4(b)所示，当蜗壳网格数大于320万之后，压比和效率都趋于稳定。综合考虑蜗壳选择320万左右网格作为数值优化计算的网格数。

图4 网格无关性验证Fig.4 Grid independence study

2.2 数值模型验证

为验证数值模型的准确性，对有公开几何数据和试验数据的Eckardt 径向叶轮[13-14]进行数值模拟，Eckardt 叶轮为半开式径向型离心叶轮，整个结构由叶轮和无叶扩压器两部分构成，设计参数见表1。进行数值验证的径向叶轮计算域如图5所示，采用上述数值方法分别计算转速为12000、14000、16000 r/min 叶轮的总体性能并将试验结果和数值计算结果进行对比，如图6所示，发现数值计算值与试验变化较为吻合，两者压比的最大相对误差在2%以内。压比随质量流量的变化规律基本一致，表明所用计算模型是可靠的，可用于进一步的计算和分析。

表1 Eckardt径向叶轮设计参数Table 1 Design parameters of Eckardt radial impeller

图5 计算域网格划分Fig.5 Diagram of grid generation in computing domain

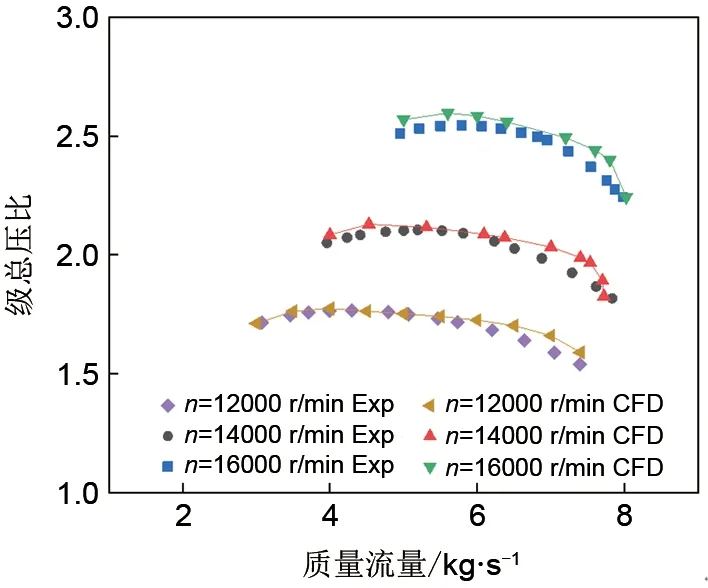
图6 试验与数值结果比较Fig.6 Comparison of experimental and numerical results

3 多目标优化设计

3.1 优化目标

静压恢复系数Cp和总压损失系数Kp是评价排气蜗壳气动性能的重要参数，定义如下

3.2 优化流程

Kriging 代理模型是一种在有限区域内对区域化变量进行无偏最优估计模型，在叶轮机械研究中获得了广泛应用[15]。代理模型的建立需要对大量样本点进行数值计算，试验设计方法中的最优拉丁超立方设计(Opt LHD)[16]可以使所有样本尽量均匀分布在设计空间，具有很好的空间填充性和均衡性。采用Opt LHD建立6变量97次试验的初始样本集，并更新设计变量来确定控制点的位置，得到控制点控制的三次B样条曲线作为新的蜗壳截面形状，得到对应97组不同截面形状的蜗壳几何文件。

离心压缩机多目标优化设计流程如图7所示。

图7 多目标优化设计流程Fig.7 Multi-objective optimization design process

（1）采用最优拉丁超立方设计生成建立Kriging模型过程中所需的样本点。

（2）将样本点对应的设计变量，写入UG表达式文件中，使用批处理命令调用UG的二次开发程序UG Update更新排气蜗壳三维模型。

（3）针对设计流量工况，通过调用编写好的UG、ANSYS ICEM、ANSYS CFX 等软件的宏命令文件，完成网格划分、前处理、CFD计算和后处理的工作，最后得到相应的设计变量组合下的性能参数。

（4）基于数值计算结果，随机选取75组(80%)样本建立设计变量关于静压恢复系数和总压损失系数的Kriging 模型，剩余20%样本对模型进行误差分析。

（5）采用NSGA-II遗传算法对建立的近似模型进行多目标优化求解，设定初始种群数为40，遗传代数为50，交叉概率为0.8，变异概率为0.2，优化问题可描述为

（6）对优化的结果进行精确数值计算，如不满足预测结果与验证结果一致，则将计算结果加入样本空间中，重复步骤(4)、(5)，直至满足终止准则，得到更优的结果。

4 优化结果与分析

4.1 优化结果

方差分析(ANOVA)R-Squared可分析用来衡量近似模型与样本点项符合的程度。在近似模型建立过程中，静压恢复系数和总压损失系数的R2项分别为0.97 和0.96，可以确定近似模型具有很好的有效性。通过评估每个个体的总压损失系数和静压恢复系数来监控遗传优化的进程，如图8所示。优化得到最佳解并进行数值计算验证，结果见表2。采用代理模型与数值计算的静压恢复系数和总压损失系数的误差均小于0.5%，满足终止准则。

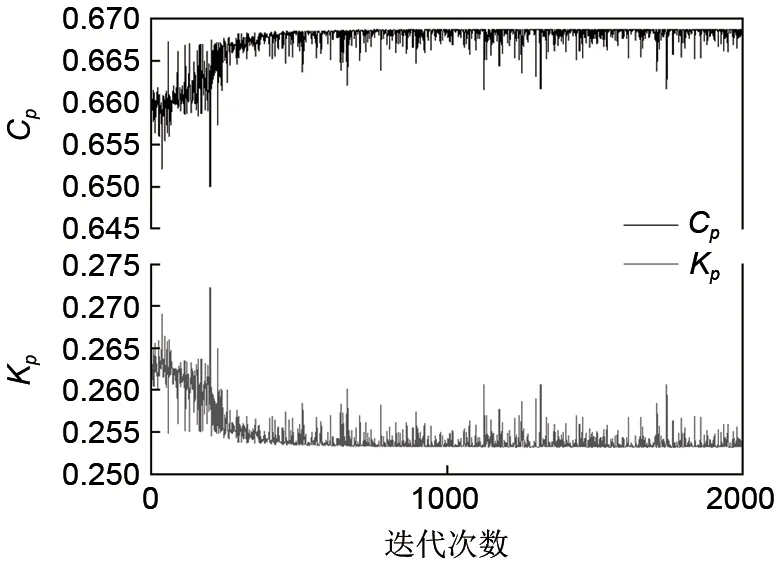
图8 遗传优化进程Fig.8 Genetic optimization process

表2 优化结果对比Table 2 Results of optimization

图9给出了优化前后排气蜗壳通流截面参数对比，从图中可以看出优化后的蜗壳截面呈现斜泪滴形。优化前后排气蜗壳周向截面面积分布如图10所示，优化后的蜗壳具有更小的出口面积。由Mishina 等[17]研究表明较大的蜗壳通道截面面积可以减少总压损失。而优化前蜗壳在较大出口面积的情况下有更高的总压损失系数，表明优化后的截面形状对蜗壳性能的提升有利，这反映出优化后的蜗壳与离心压缩机叶轮和有叶扩压器之间得到了更好的匹配。图11 为优化前后离心压缩机整体性能曲线对比，与优化前相比，优化后压缩机在设计工况和非设计工况下的效率和压比均有所提升，在设计工况下等熵效率提高了0.45%，压比提高了0.36%，整体性能得到了一定程度改善。

图10 蜗壳周向截面面积分布Fig.10 Area distribution of volute circumferential cross section

4.2 流场分析

为了分析优化前后蜗壳内部流动特性，选取蜗壳周向4 个截面为分析对象。图12(a)、(b)给出了设计工况下蜗壳周向不同截面优化前后的总压损失系数和静压恢复系数分布云图，可以看出在90°截面蜗壳和扩压器内存在一部分静压恢复系数小于零的区域，对比速度矢量图这部分涡流速度较高，导致扩压器内提升的静压在蜗壳内被消耗，这些区域的压力要小于扩压器出口的平均静压。与优化前相比，优化后蜗壳截面内Cp小于零的区域相对较小，进口区域流体静压耗散的较少。从周向不同截面Cp上的分布情况可以看出，在远离蜗壳进口区域静压恢复系数较大，这是角动量守恒和由周向速度产生的离心力导致的压力分布沿径向增加。与优化前相比，优化后静压恢复系数在270°和360°截面上升明显。

图11 优化前后离心压缩机整级性能曲线对比Fig.11 Characteristic curve before and after optimization

优化之后蜗壳不同周向截面总压损失系数都得到一定的降低，对比发现截面中心的总压损失有明显降低。从180°到360°截面可以看出，与其他位置相比，截面中心具有较高的总压损失，这是由截面中心区域旋涡流动引起的高剪切应力造成的。在90°截面优化前后都没有出现刚体涡旋结构，高的总压损失出现在蜗壳径向内壁。优化前后蜗壳的性能差异也是由于蜗壳截面几何形状差异产生的不同涡结构引起的剪应力损失的变化造成的。泪滴形的截面形状在一定程度上减小了旋涡中心的剪切应力。

从截面速度矢量图13 可以看出，扩压器段的速度相较蜗壳内速度高，速度梯度也较大。优化前蜗壳进口区域速度梯度较大，不同速度流体之间由于黏性和掺混造成了较大的损失。在蜗壳入口下游的射流都会在蜗壳通流截面中产生一个稳定的大涡结构。优化前的模型中，在扩压器和蜗壳进口区域通流速度较大，而优化后的蜗壳内进口区域流动更为均匀。总的来说，优化后的蜗壳通流速度较低，其蜗壳内部的速度分布更为均匀。

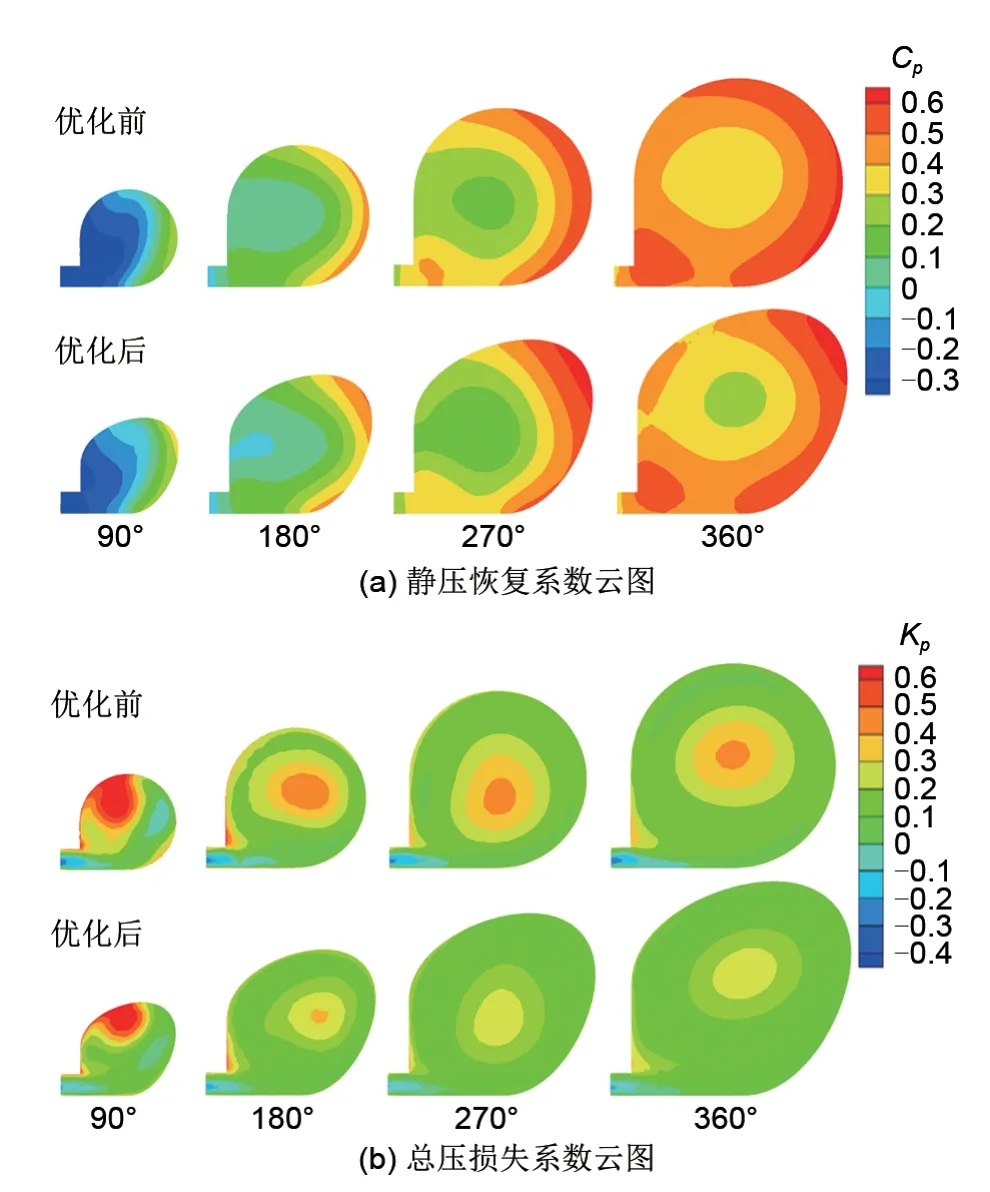
图12 优化前后蜗壳周向截面流场对比Fig.12 Comparison of flow field in circumferential cross section before and after optimization

图13 优化前后速度矢量Fig.13 Diagram of velocity vector before and after optimization

5 结 论

以先进压缩空气储能系统离心压缩机为研究对象，在对排气蜗壳进行匹配设计的基础上，采用NSGA-II遗传算法对蜗壳通流截面参数化的离心压缩机进行三维多目标优化设计，得到如下结论。

（1）建立了一种针对先进压缩空气储能系统用离心压缩机切向进口外蜗壳的截面参数化方法，综合截面形状和面积，实现了蜗壳截面控制变量的参数化。

（2）结合Kriging 近似模型和多目标遗传算法对参数化蜗壳建立的优化模型能很好地代替数值分析的结果。经数值验算结果显示，在设计工况下优化后排气蜗壳的静压恢复系数提高了5.52%，总压损失系数减小了11.24%。与初始设计相比，整级等熵效率提高0.45%，压比提高0.36%。

（3）优化后泪滴形的截面形状可以减小旋涡中心的剪切应力，使排气蜗壳内部通流速度分布更加均匀，从而减小了蜗壳内部的总压损失。