基于飞蛾火焰算法的AUV三维全局路径规划

徐炜翔,朱志宇

（江苏科技大学 电子信息学院，镇江 212003）

自主水下航行器（autonomous underwater vehicle，AUV）的路径规划是海洋探索和科学研究的关键问题。由于海洋环境的复杂性，研究能够在水下三维环境和复杂海流下实现自主路径的AUV路径规划方法已成为研究热点[1]。AUV全局路径规划的主要过程是将整个路径划分为若干个子路径点，使AUV能够沿着子目标点构成的无碰路径安全地移动到终点[2]。近年来，关于AUV路径规划的研究越来越多，例如：使用改进的蚁群算法[3]、A*算法[4]、人工势场算法[5]、快速扩张随机树算法[6]等。Zhu等[7]提出了一种基于生物启发自组织图的方法，实现了AUV的路径规划和自主导航。Yan等[8]提出了一种改进粒子群优化方法，用于二维平面障碍环境中AUV归航和对接任务的自主路径规划。孙叶义等[9]全面阐述了AUV路径规划的实际困难，总结了目前成熟的规划方法。

目前大多数研究成果将AUV的路径规划问题限制在二维环境中，而对于实际三维空间中的路径规划研究更有意义[10]。尤其是在复杂的海底地形和存在海流干扰的情况下，基于传统方法的规划方式极大地增加了AUV不必要的能量损耗，降低了使用寿命，甚至导致AUV无法正常运行。曹翔等[11]将速度合成方法与生物自组织神经网络相结合，用于三维水下工作空间，同时考虑了各种情况的海流因素，以最小能耗为代价函数，从而有效地解决了海流对AUV的影响。但是，这种方法在遇到复杂障碍物时运行效率缓慢，难以应用于实际任务。在海洋环境下，各类复杂的海洋环境因素需要被考虑到规划问题中，如海流、涡流、盐度、温度等。若能将各类环境影响因素信息采集处理并加以利用，则可极大地提高路径质量，扩展更多的应用范围。

启发式算法已被广泛地用于机器人路径规划，如粒子群优化算法[12]、人工蜂群算法[13]、布谷鸟搜索算法[14]等。Mac等[15]全面分析和比较了各种启发式算法在路径规划中的应用，总结了每种启发式算法的优缺点。这些传统的启发式算法主要受结构复杂、参数多、全局搜索能力不强，以及过早收敛的限制，难以达到期望的规划效果。2015年，Mirjalili[16]提出了一种新的启发式算法，即飞蛾火焰优化（moth-flame optimization，MFO）算法，其灵感来自于飞蛾的特殊导航方法。飞蛾在自然界中使用一种称为侧向定位的特殊机制来与月球保持固定角度，以保证直线飞行。但是在人造光下，它们将以螺旋路径环绕点光源，最终汇聚在光源上。在MFO算法中，飞蛾和火焰的位置都是搜索空间中可行的解，其中火焰是飞蛾目前搜索到的最佳位置，通过不断更新飞蛾的位置来搜索最优解。飞蛾位置的螺旋更新机制确保了飞蛾不会丢失最优解，同时保证了极高的搜索效率。作为一种全新的启发式算法，MFO算法相较于传统启发式算法在搜索速度和全局性上有明显优势，且已经在工程领域得到了广泛运用，并取得了很多成果[17]。所以将MFO算法运用在路径规划领域有广阔的前景。

本文重点研究水下三维复杂环境和静态海流下的AUV路径规划问题，提出了一种基于MFO算法的AUV全局路径规划方法。结合AUV自身能耗模型，设计出基于能耗最优的适应度函数。根据飞蛾位置更新机制，调整路径点位置，不断迭代得到最佳路径。

1 环境模型构建

1.1 三维地形模型

环境建模是路径规划的基础部分。假设海洋环境地图数据是已知的。采用栅格法对已知深度数据的X轴和Y轴进行插值来获得初始地形，将水平面与XOY重合，设定AUV沿X轴前进[18]。所得水下三维地形环境如图1所示。

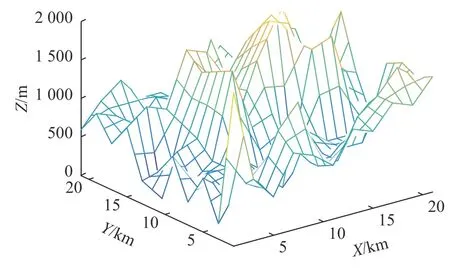
图1 三维路径规划空间Fig. 1 Three-dimentional path planning space

1.2 静态海流模型

考虑到AUV在真实的海洋环境中航行会受到海流、波浪和风等各种环境因素的影响，其中波浪和风的影响在水平面2 m以下可以忽略不计，所以仅考虑海流对AUV运动的影响[19]。由于地球的自转效应，海流在水平面中的运动要比垂直面中的运动大得多，所以假设海流在垂直方向上的速度为零，将海流视为在二维水平面中的运动。将空间纵轴Z按照深度分层，每层都是一个XOY的二维平面。在该平面进行网格划分，每个网格是一个边长为1 km的正方形，单个网格的海流因为变化幅度极小而被视为常值。海流模型的数值方程由多个粘性涡流函数叠加表示[20]，其数学描述如下：

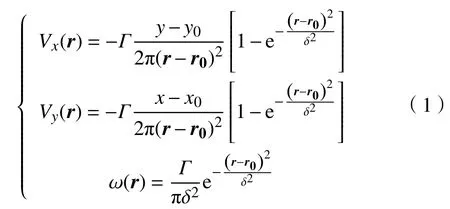
式中：r，r0分别为当前位置和涡流中心的坐标矢量；δ为涡流半径；Γ 为涡流强度；Vx(r) ，Vy(r)分别为水平方向和垂直方向的涡流速度分量。本文仅考虑海流随空间变化的情况，假设在AUV任务期间单位海流在区域中是恒定的。文中假设的海流参数分别为：δ=1.0 ；Γ=10；涡流中心矢量r0取平面空间中3个随机坐标点。所生成的海流势场如图2所示。

图2 海流空间势场Fig. 2 Spatial potential field of ocean currents

2 AUV能耗模型

AUV的总能耗由AUV在静态环境下的移动能耗和海流影响下的能耗叠加而成[21]。首先，建立AUV的水阻力与航行速度的方程、推进器推力与效率的方程，计算获得AUV在静态条件下移动时计划路径的总能耗；然后，将从流场函数获得的当前海流速度矢量添加到AUV航速模型中，求得AUV的真实航速；最后，将真实航速带入到能耗方程中，获得在当前环境中移动的AUV总能耗。

由于全局路径规划基于先验的水深环境数据，仅考虑地形深度数据即静态障碍物，而不考虑移动障碍物，因此，AUV在获得的路径子目标点间行驶，忽略了明显的转向动作。为了简化计算的复杂度，假设：

a.AUV在整个航行过程中以恒定的速度直线行驶，忽略了路径初始阶段的加速和路径终点阶段的减速；

b.AUV全局路径基本平滑，忽略航行过程中由转向引起的减速和加速过程。

AUV在水下航行时主要克服水阻力。根据流体力学公式，AUV所受的水阻力Fz为

式中：C为流体动力系数，其值与传播介质、机器人的形状等因素有关，根据一般经验取0.7；ρ为水体密度；v为AUV的航行速度；S为AUV的横截面积，本文中试验原型机的横截面积为0.0625 m2。根据式（2）可得

当AUV在静态环境中移动时，忽略AUV推进器外部所有组件的能量损耗，假设AUV的所有能耗都是为了克服水阻力。在匀速运动时，水阻力等于推进器推力。因此，在计算能耗时，可以使用上式来构建能耗函数。根据牛顿第二定律，AUV在恒定速度下的合力应为零，即螺旋桨产生的推力等于水阻力。本文中AUV原型的推进器使用Maxon无刷直流电动机。经过试验测试，采用二次函数拟合得到推力Ft与输出功率P的对应关系为

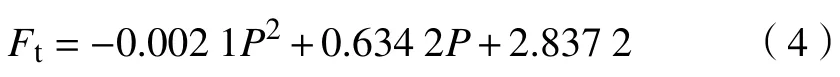
Maxon推进器使用无刷直流电动机，具有独特的机械特性，即在一定速度范围内，随着电动机速度的增加，机械效率会逐渐提高。在忽略其余部件能量消耗的情况下，即AUV所有能耗等于电机能耗。此时，AUV的航行速度与推进器的工作效率η存在以下对应关系：

将式（2）与式（4）代入式（5），可得AUV速度与工作效率的对应关系

AUV在静态环境下匀速巡航期间的能耗为

式中：t为航行时间；L为航行距离。将式（2）、式（6）带入式（7），得到AUV的总能耗公式为

根据上式可知，除航行速度与航行距离外，其余参数均是常数，所以AUV的能量消耗仅与AUV的航行速度和航行距离有关。

3 基于MFO算法的路径规划

类似于布谷鸟算法和蜂群算法等启发式算法，MFO算法是一种基于飞蛾行为的新型启发式算法。MFO算法模拟了自然界中飞蛾的导航行为，是一种称为横向定位的特殊夜间导航方法[22]。在该算法中，假设候选解是飞蛾，问题的变量是飞蛾在空间中的位置。飞蛾和火焰都是解决方案，它们之间的区别在于它们在每次迭代中的处理和更新方式。飞蛾是在搜索空间中移动的实际搜索媒介，而火焰是迄今为止获得的飞蛾的最佳位置。MFO算法结构简单，主要依靠对数螺旋函数的飞蛾位置更新机制、火焰序列的迭代更新和种群数量的自适应机制来实现优化。试验表明，MFO在解决受到位置搜索空间约束的问题方面比其他启发式算法具有明显优势。该算法在路径规划中的过程如下。

3.1 种群初始化

首先，在搜索空间中随机生成若干飞蛾的空间位置。在路径规划的任务空间中，一只飞蛾代表一条初始路径，所以飞蛾的位置是一个矩阵向量。根据AUV的起点和终点信息，沿X轴划分搜索空间以形成若干个YOZ平面。根据启发式信息在每个YOZ平面中随机选择生成下一个路径点，在满足避碰的前提下，将所有子路径点连接产生一条初始路径。飞蛾的位置矩阵M和所有飞蛾的适应度值矩阵OM为

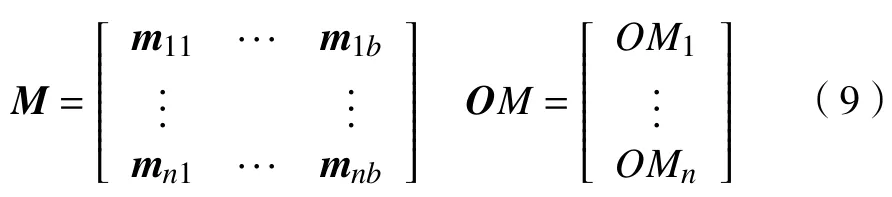
式中：mnb为飞蛾的位置向量，n代表飞蛾种群的飞蛾数量，b代表飞蛾位置向量的维数；OMn为对应飞蛾n的适应度值。将每个飞蛾的位置向量传递给适应度函数，并将结果输出分配给相应的飞蛾作为适应度值，构成飞蛾适应度值矩阵。

火焰矩阵与飞蛾位置矩阵的结构相似，同样由每个火焰的位置向量组成。飞蛾充当在搜索空间中不停移动的搜索单元，而火焰是有史以来飞蛾搜索到的最佳解，在找到更好的解决方案后，火焰位置就会更新。火焰适应度零值矩阵根据每个火焰适应度值进行排序得到。火焰的位置矩阵F和所有火焰的适应度值矩阵OF为

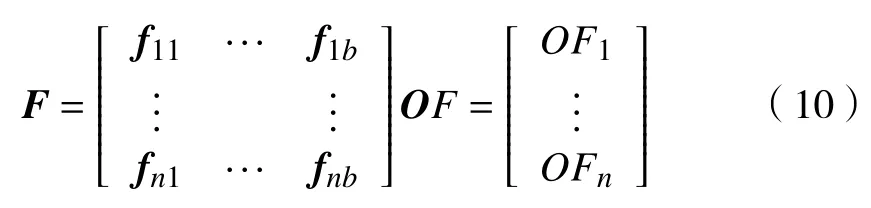
式中：fnb为火焰的位置向量，n代表火焰数量，b代表火焰位置向量的维数；OFn为对应火焰n的适应度值。

用于生成初始路径的启发值由两部分组成：一部分用来判断下一个点是否可达，即是否符合避碰条件；另一部分用来计算下一个点到当前位置的距离与下一个点到目标点的距离之和。这两个量的乘积作为启发式值得到可行的初始路径。每条路径包括21个子路径点，每个子路径点都由Y轴坐标和Z轴坐标表示，因此每个飞蛾都是一个具有42个维度的列向量。

3.2 位置更新

飞蛾的位置更新机制是MFO算法的核心部分。飞蛾个体不断迭代以更新其在火焰周围的位置，直到找到最佳解决方案为止，而其数学描述又分为扑焰行为和弃焰行为两部分。

a.扑焰行为

自然界中具有趋光性的飞蛾依靠横向定位导航机制向距离最近的光源移动，其飞行轨迹呈螺线型。选择数学描述如下的对数螺旋作为飞蛾的

运动轨迹：

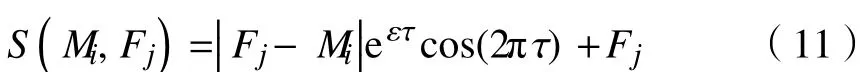
式中：S(Mi,Fj)为更新后的飞蛾位置，其中Mi为飞蛾位置，Fj为光源位置；|Fj−Mi|为飞蛾到火焰的距离；ε为与螺线形状相关的常量；τ为随机数，取值区间为[−1,1]，τ=−1表示最接近火焰的位置，τ=1表示离火焰最远的位置。

b.弃焰行为

MFO算法通过放弃火焰数量的机制来保持最佳火焰位置，自适应地减少火焰数量的过程如下所示：

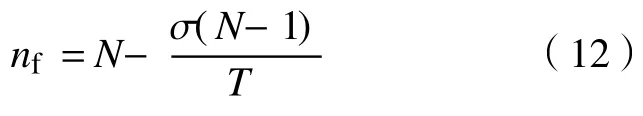
式中：N为初始火焰数量；σ为当前迭代次数；T为最大迭代次数。在迭代T次之后，火焰数量为1，即代表所得到的全局最优解。

3.3 适应度函数

代价函数是计算飞蛾适应度值的适应度函数，也是目标优化函数。采用式（8）对每个栅格内航行的能耗进行求和得到总能耗作为代价函数。

从式（8）可以知道，AUV在自身航行速度范围内的速度越高，其能耗越低，因此假定AUV以期望航速2.5 m/s（最大速度）做匀速航行。在海流环境中，AUV的实际速度是最大静态水流速度与AUV航行方向上的速度之和，可由下式计算：

式中：Ve为期望航速矢量；Vc为海流流速矢量，由式（1）获得；cos(Ve,Vc)为Ve与Vc之间的夹角余弦值。最终将v带入式（8）得到AUV的总能耗。

4 仿真试验

本文重点研究在海流影响下的复杂海洋环境中AUV的全局路径规划问题。为了验证该方法在AUV路径规划中的优越性，在Matlab R2016b软件平台上设计了一系列仿真试验。首先整个规划空间 为21 km×21 km×20 km，分 为21×21×20个独立网格。AUV的初始位置坐标是（1，10，4），目标位置坐标是（21，8，5），由于AUV的体积与空间相比可忽略不计，因此将其视为空间中的质点。设定飞蛾火焰算法的基本参数分别为：飞蛾种群数量100，最大迭代次数3000。与同等条件下蚁群优化算法（ACA）算法的三维路径规划结果作对比。

4.1 静态环境

第一种情况是在由深度数据得到的静态地形障碍环境下规划从起点到终点的路径。在这种情况下，不考虑海流对AUV的影响，并且假定AUV在整个航行过程中速度保持恒定不变。根据式（8）可知，此时AUV的能量消耗仅与路径长度有关，因此将所规划路径的长度用作目标优化函数，距离最短的路径即是能量消耗最低的路径。图3是MFO算法在静态水环境中的路径规划结果，图4是ACA算法在静态水环境中的路径规划结果。MFO算法与ACA算法的基本参数设定和结果如表1所示。

图3 静态环境下MFO算法路径规划Fig. 3 Path planning in static environment using MFO algorithm

图4 静态环境下ACA算法路径规划Fig.4 Path planning in static environment using ACA algorithm

从表1可知，虽然MFO算法搜索用时较ACA算法长，但是由于AUV全局路径规划对实时性要求不高，故可以满足全局路径规划的需要。

从图3和图4的比较可以看出，MFO算法所规划的路径是十分平滑的。由于ACA算法中蚂蚁单元的运动规则使蚂蚁只能在整数坐标点之间运动，导致ACA算法规划获得的路径不是全局最优解。由于MFO算法中飞蛾独特的位置更新机制，使该算法可以探索空间中的任何点，这满足了AUV对平滑路径的需求。

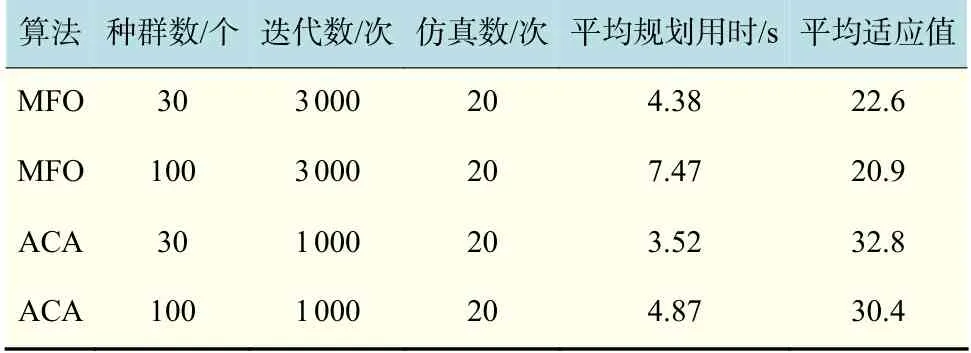
表1 规划算法的参数设定与结果Tab.1 Parameter settings and results of planning algorithm

图5为MFO算法和ACA算法的适应值曲线。可以看出，MFO算法的适应度值在开始时会很快收敛，收敛速度在经过200次迭代后会逐渐变缓，最终在迭代1000次左右时收敛到全局最优值。ACA的适应值呈阶梯状变化，在前200次迭代中迅速收敛，在200次后陷入局部最优，之后很长时间不再变化。ACA的最终适应度值比MFO算法的最终适应度值高得多，这主要因为ACA算法通常会进入局部最优状态，很难逃脱。而MFO算法的强大之处在于其出色的全局优化能力。由于MFO算法中的火焰会保留每个飞蛾的最佳位置，因此飞蛾永远不会失去其最佳搜索结果。随着搜索次数的增加，飞蛾适应度值将逐渐收敛到最优值，而不会陷入局部最优解中，这些功能在AUV全局路径规划中非常有用。尽管MFO算法需要更多的运行时间和更长的迭代时间，但是由于全局计划对实时性需求不强，因此该算法非常适合AUV全局路径规划。

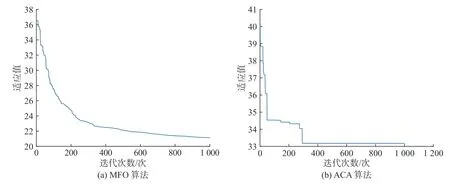
图5 适应值曲线Fig.5 Adaptation value curve

4.2 海流环境

第二种情况是AUV在海流环境中从起点到终点的路径规划。在这种情况下，不仅应考虑地形障碍，还要考虑海流对AUV的影响。此时，AUV在不同栅格内的速度将发生变化。AUV的实际速度根据式（13）求得，代入式（8）得到总能耗作为代价函数。仿真结果如图6、图7所示，在20次仿真试验中，路径规划所需的平均时间为10.6 s。

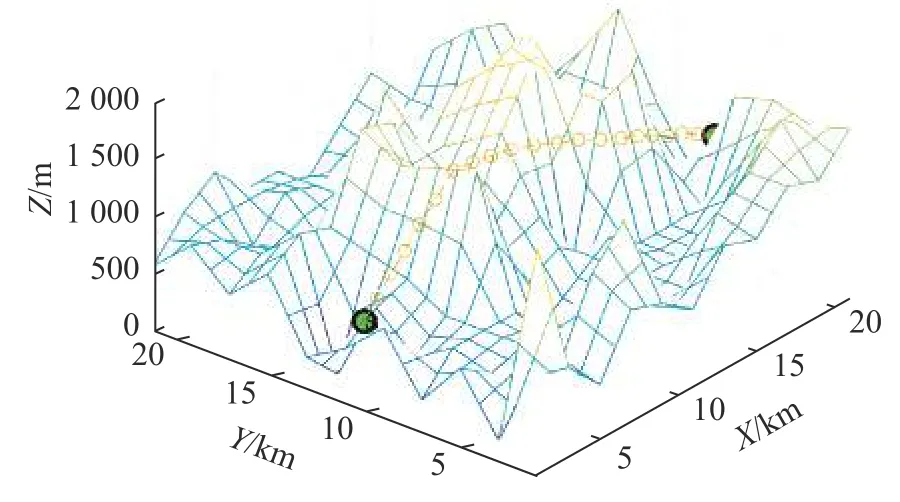
图6 MFO算法海流环境下路径规划Fig.6 Path planning in ocean current environment using MFO algorithm

图7 MFO算法规划俯视图与相关海流场Fig.7 Plan top view and related currents field using MFO algorithm

如图7所示，MFO算法所规划路径尽可能避免了逆流对AUV的减速作用，并充分利用了顺流对AUV的加速作用，获得了最低能耗代价的路径，其全局优化能力十分优异。试验证明，MFO算法在路径规划中表现出色。

5 结 论

研究了三维水下环境中AUV全局路径规划问题。综合考虑了海流和地形障碍的影响，建立了由AUV静态能耗模型和海流影响下能耗模型的综合能耗优化目标函数，将MFO算法应用在解决路径规划的非线性优化问题中。仿真结果表明，MFO算法在全局搜索寻找最优解时有出色表现，不会因过早收敛陷入局部最优，证明了该方法的可行性和实用性。尽管具有上述优点，但仍有许多现实因素需要考虑。例如，本文中使用的海流模型相对简单，没有考虑时变海流等复杂情况。将来仍然需要对这些问题进行进一步的研究。