泊肃叶流下中性浮力颗粒横向迁移的研究进展
叶 挺,凡凤仙
(上海理工大学 能源与动力工程学院,上海 200093)
管道内颗粒负载流动是能源、化工及生命科学等领域的研究热点之一。颗粒横向迁移是管道内颗粒负载流动中的一种有趣现象,它是指随机散布在泊肃叶流中的中性浮力颗粒(密度与流体密度相同的颗粒),经过一定时间后,迁移到距管中心一定距离横向位置上流动的现象[1]。颗粒横向迁移现象有望在颗粒的分离、筛选、混合、反应中得到应用[2-3],富有研究价值和应用潜力。颗粒横向迁移的早期研究主要采用实验方法,且多关注雷诺数、颗粒尺寸等对颗粒迁移的最终平衡位置的影响。随着计算机和数值模拟技术的发展,数值模拟逐渐成为研究颗粒负载流动的重要手段,通过数值模拟可以方便地对参数进行调整,且能够获取丰富的流场和颗粒动态过程的细节信息,便于揭示相关现象的规律及内在机理。近年来,多种数值模拟方法在颗粒横向迁移研究中得到应用,并取得了一些有价值的研究成果,但由于颗粒横向迁移所涉及的液固两相流场的复杂性,目前对颗粒横向迁移行为的认识仍存在争议,对横向迁移内在机理研究还不够深入。本文首先针对泊肃叶流下中性浮力颗粒横向迁移的相关实验和数值模拟研究进行归纳和评述,然后基于直接力/虚拟区域(direct-forcing fictitious domain,DF/FD)方法模拟再现单个颗粒横向迁移的过程,在此基础上指出今后进行颗粒横向迁移研究的思路和方向。
1 泊肃叶流下中性浮力颗粒横向迁移的实验研究
1.1 圆管内颗粒横向迁移的实验研究
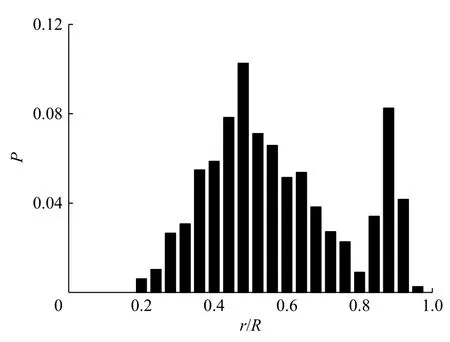
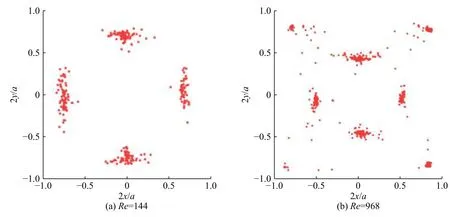
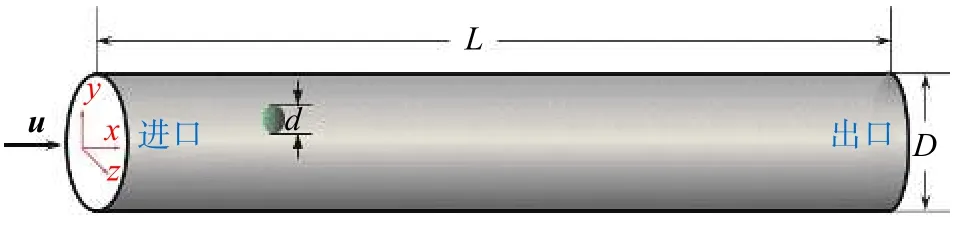
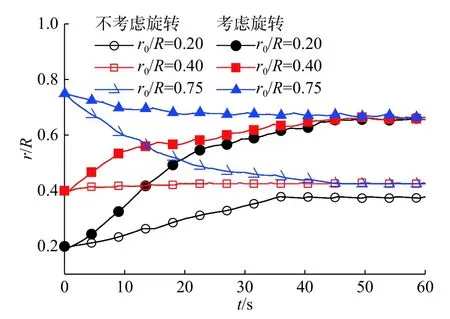
1961年,Segré和Silberberg[4]首次在实验中观察到圆管内低雷诺数(7 图1 横向迁移后颗粒浓度沿径向的分布Fig. 1 Particle concentration as a function of radial position after lateral migration 随后,一些学者迅速开展了不同条件下圆管内颗粒横向迁移平衡位置的探讨。1962年,Oliver[5]通过实验发现颗粒的旋转对于颗粒迁移的最终稳定位置有显著影响,无旋转时颗粒最终稳定位置更接近管中心轴线,并认为向内的壁面效应与向外的马格努斯效应使得颗粒最终稳定在特定的径向位置。1965年,Jeffrey等[6]在圆管直径D=32.5 mm,颗粒直径d=1.5,2.0,2.9 mm的条件下,实验观察到中性浮力颗粒最终迁移到距管中心轴线约为2R/3的环形区域。1966年,Karnis等[7]通过实验发现中性浮力刚性颗粒横向迁移的平衡位置与颗粒形状、粒径和管径比有关,中性浮力可变形颗粒总是迁移到管中心轴线位置。 然而,由于受实验技术的限制,难以得到更为详细的颗粒动力学信息和流场信息,相关实验研究一度停滞。直到进入21世纪,微流控技术兴起,泊肃叶流下中性浮力颗粒的横向迁移重新引起了学者的重视。2004年,Eloot等[8]实验研究了颗粒直径d=10 μm的近中性浮力球形颗粒在直径D=220,530 μm的毛细管内的运动,结果表明,在较高的雷诺数、较长和较细的毛细管、较稀的颗粒浓度的条件下,颗粒横向迁移的平衡位置更接近于管壁。2004年,Matas等[1]实验研究了雷诺数Re在67~1700范围以及达到2 000时,圆管内稀相泊肃叶流下中性浮力球形颗粒(D/d=8~42)的横向迁移,发现Re较小时,颗粒迁移到距管中心轴线一定距离的环形区域,随着Re的增大,环形区域的位置向管壁移动,当Re继续增大到一定值时,颗粒的迁移使得颗粒分布在2个环形区域,即除了靠近管壁的外环外,还存在一个靠近管中心的内环。图2给出了Matas等[1]实验得到的Re=1000时颗粒概率密度P沿径向的分布情况,可见内环出现在r/R≈0.5处,外环出现在r/R≈0.9处。2017年,Morita等[9]实验研究了雷诺数Re在100~1100范围、颗粒粒径与管径比约为0.1时,泊肃叶流下中性浮力颗粒横向迁移的平衡位置,研究发现,Re较大时,颗粒分布首先集中在2个环形(即内环和外环)区域,随着颗粒向下游运动,内环附近颗粒减少,而外环附近颗粒增加,若管道足够长,颗粒将最终迁移到外环位置。Morita等[9]得到了较大雷诺数下颗粒迁移特性的演变过程示意图,如图3所示,即随机分布的颗粒随流体进入管内(x=0),首先向内迁移到达一定的位置(x=L2);接着转而向外迁移,引起颗粒在内环和外环2个区域集中(x=L1);颗粒继续向外迁移,最终集中在一个环形区域(x=L0)。在图3中,颗粒向内迁移发生在流体从初始状态充分发展为泊肃叶流的管段,这表明颗粒起初向内迁移与流动的发展过程有关,颗粒转而向外迁移则是由于泊肃叶流中横向速度梯度引起的升力和颗粒的旋转引起的升力所致。 图2 横向迁移后颗粒概率密度沿径向的分布Fig.2 Particle probability density as a function of radial position after lateral migration 图3 较大雷诺数下颗粒迁移特性的演变过程示意图Fig.3 Schematic diagram of the evolution of particle migration at relatively high Reynolds number 由于壁面效应的影响,非中心对称的矩形和方形截面通道内颗粒横向迁移的特性将与中心对称的圆管不同,一些学者针对矩形与方形截面通道内颗粒的横向迁移开展了一系列研究。 在矩形截面通道泊肃叶流下颗粒横向迁移的研究方面,2005年,Staben等[10]实验研究了雷诺数Re(以矩形窄边长H作为特征尺寸)在0.005~0.05范围时颗粒粒径对不同管口形状的矩形截面微通道内颗粒横向迁移的影响,结果表明,小粒径颗粒(0.07≤d/H≤0.10)在直管口通道内向通道中心迁移,在带倒角管口通道内分布更为均匀;中等尺度粒径颗粒(0.46≤d/H≤0.54)在直管口和带倒角管口通道内均呈几乎均匀的分布;少量大粒径颗粒(0.79≤d/H≤0.95)的分布略微向通道的一个侧壁倾斜。2008年,Bhagat等[11]在Re>1的条件下实验研究了矩形截面微通道内颗粒的横向迁移特性,结果表明,颗粒迁移过程主要取决于通道截面较短边的几何尺度,颗粒最终分布在较大的壁面附近,d/H=0.07情况下,Re≥ 10时才能发生横向迁移,且随着d/H的增加,颗粒横向迁移所需要的临界雷诺数降低。由于文献[10-11]的实验中采用的雷诺数范围有很大差异,使得实验结果不同,雷诺数对矩形微通道内颗粒横向迁移的影响仍需要进一步系统的研究。 在方形截面通道泊肃叶流下颗粒横向迁移的研究方面,2008年,Kim等[12]实验研究了通道雷诺数Re在0.06~58.65范围内中性浮力颗粒(通道水力直径与粒径之比λ≈14)的横向迁移,结果表明,在很低的雷诺数下,颗粒的横向迁移仍会发生,存在一个在20~30之间的临界雷诺数Rec,当Re 图4 典型雷诺数下横向迁移后的颗粒分布Fig.4 Particle distributions after lateral migration at typical Reynolds numbers 为了理解颗粒横向迁移的机理,1979年,Aokl等[15]实验研究了基于颗粒自由沉降速度的雷诺数ReF(ReF=2r'uF/ν,r'为颗粒半径,uF为颗粒在静止流体中的自由沉降速度,ν为流体运动黏度)在0.043~10范围时非中性浮力颗粒在圆管内的横向迁移,结果表明,ReF>1时,若颗粒运动滞后于流体,则颗粒向管中心轴线迁移,若颗粒运动超前于流体,则颗粒向管壁迁移,这一现象受控于Magnus效应;ReF<1时,靠近管壁的颗粒向内迁移,靠近管中心的颗粒向外迁移,最终颗粒到达管壁和管中心轴线之间的一个平衡位置,这一现象是由壁面效应和惯性作用共同引起的。为了探讨颗粒横向迁移在微流控领域的应用,2011年,文献[16]基于螺旋微通道内惯性升力和Dean曳力共同作用下,不同粒径颗粒发生横向迁移的最终平衡位置不同的原理,设计出利用螺旋形通道富集和分离颗粒的微流控装置。2012年,Martel等[17]实验研究了高宽比在0.125~1范围的螺旋形微通道内颗粒富集动力学行为,给出了实现高质量富集所需要的通道长度和流速范围。这些研究可以为理解颗粒横向迁移的机理以及开发基于横向迁移原理的微流控装置提供参考。 与实验研究相比,管道内中性浮力颗粒横向迁移的数值模拟研究开展得较晚,但由于数值模拟的迅速发展以及计算机能力的快速提升,数值模拟已成为研究颗粒横向迁移行为及其内在机理的重要手段。目前,研究颗粒横向迁移的数值模拟方法主要有有限元方法、虚拟区域方法、格子波尔兹曼方法及界面追踪方法等。 1994年,Feng等[18]对泊肃叶流下中性浮力圆形颗粒的运动进行二维有限元模拟,获得了与文献[4]的实验类似的颗粒横向迁移效应,并将颗粒横向迁移的驱动力归因于润滑产生的壁面排斥力、剪切滑移产生的惯性升力、颗粒旋转产生的升力和速度曲线的曲率产生的升力。 2009年,文献[19]利用有限元方法求解稳态纳维−斯托克斯方程,通过表面积分的方法获得颗粒受到的力和力矩,对狭窄矩形截面微通道内颗粒横向迁移进行数值模拟,并进行了相应的实验,数值模拟得到的颗粒横向迁移的平衡位置与实验结果吻合良好。在此基础上,模拟了颗粒横向迁移过程中的升力,分析了升力的标度关系。 2005年,Yang等[20]采用虚拟区域方法,通过固定网格分布式拉格朗日乘子描述颗粒的运动,模拟了管内单个中性浮力刚性颗粒的横向迁移,得到的颗粒平衡位置与实验吻合良好。2008年,Pan等[21]采用基于拉格朗日乘子的虚拟区域方法模拟三维泊肃叶流中的中性浮力椭圆形颗粒的运动,研究了颗粒的旋转和取向特性,发现随着雷诺数和颗粒形状的变化,颗粒呈现截然不同的运动状态,颗粒横向迁移的平衡位置与文献报道的圆盘形颗粒的实验结果[7]类似。上述方法又称为DLM/FD(distributed-Lagrange-multiplier fictitious domain)方法,该方法需要显式计算拉格朗日乘子进而计算颗粒的运动参数,因而计算效率不高。 为了提高虚拟区域方法的计算效率,直接力/虚拟区域(direct-forcing fictitious domain,DF/FD)方法被提出,该方法引入体积力以计算颗粒的运动参数,从而避免了对拉格朗日乘子的依赖。2008年,Shao等[22]在流动方向上施加周期性边界条件,利用DF/FD方法模拟了圆管泊肃叶流下球形中性浮力颗粒的运动过程以及颗粒运动对流场的影响,发现在雷诺数高于临界值时颗粒横向迁移到一定的平衡位置,这与文献[1]的实验结果在定性上一致。2009年,Sun等[23]采用DF/FD方法模拟了二维通道内的圆形中性浮力颗粒在恒定压力和波动压力驱动的流动中,横向迁移过程以及颗粒附近的流场状况,但缺少和实验结果的对比验证。 2006年,Chun等[24]采用格子波尔兹曼方法(lattice Boltzmann method,LBM)模拟雷诺数在100~1000范围的中性浮力颗粒在方形截面管道内的迁移,通过计算颗粒边界节点上动量的变化得到颗粒受到的力和力矩,数值模拟得到的方形截面管道内单个颗粒迁移的平衡位置与实验报道[1]的圆管内颗粒迁移的平衡位置基本一致。研究发现,受雷诺数的影响,颗粒可以迁移到拐角或边界中心的若干个平衡位置。2009年,Gupta等[25]利用LBM模拟了矩形截面通道内的中性浮力颗粒的惯性迁移,发现颗粒平衡位置受到雷诺数和通道横截面高宽比的影响,并将模拟结果与已有文献报道的实验结果[1]进行对比分析。 2019年,Liu等[26]采用LBM-DEM(discrete element method,DEM)耦合对二维平面泊肃叶流下中性浮力颗粒的横向迁移进行数值模拟,研究发现,颗粒浓度对横向迁移特性的影响主要取决于雷诺数Re,Re<20时,在颗粒体积分数不超过5%时才能观察到颗粒的迁移现象,Re>20时,在颗粒体积分数高于20%时仍然能够发生颗粒迁移,并提出了富集数以表征颗粒惯性迁移的程度。数值模拟得到的单个颗粒横向迁移的无量纲平衡位置随雷诺数的变化关系与实验结果[1]吻合良好。 2011年,Nourbakhsh等[27]采用有限差分/界面追踪方法模拟了三维可变形液滴在平面泊肃叶流中的运动,研究了毛细数(黏性力与界面张力的比值)、雷诺数、体积分数对液滴最终稳定位置的影响,数值模拟得到的通道截面上颗粒浓度分布与已有实验基本一致。2013年,Khalili等[28]利用界面追踪方法数值模拟了泊肃叶流中二维浮力液滴的惯性迁移,研究了弗劳德数(浮力与惯性力的比值)、雷诺数、毛细数、液滴与流体的密度比对液滴最终平衡位置的影响,然而模拟结果未得到实验的证实。2013年,Bayareh等[29]利用有限差分/界面追踪方法模拟了泊肃叶流中可变形非中性浮力液滴发生惯性迁移的平衡位置,研究发现,对于轻微浮力液滴,平衡位置在壁面和管道中心线之间。如果液滴滞后于流体,平衡位置接近中心线;如果液滴超前于流体,则平衡位置接近壁面。随着雷诺数的增加,较轻液滴的平衡位置稍微接近于壁面,较重液滴的平衡位置则更接近中心线,但是,模拟预测结果仍有待实验验证。 2005年,Yang等[20]采用任意拉格朗日−欧拉动网格技术描述颗粒的运动,模拟了管内单个中性浮力刚性颗粒的横向迁移,得到的颗粒平衡位置与实验吻合良好。 2005年,Cho等[30]利用纳维−斯托克斯方程与颗粒运动方程耦合的直接数值模拟方法研究二维通道内颗粒负载流动,证实了已有实验中观察到的颗粒横向迁移现象,研究了通道尺寸与颗粒粒径之比对颗粒平衡位置的影响。 2015年,Pazouki等[31]在拉格朗日−拉格朗日方法框架下,利用光滑粒子流体动力学方法(smoothed particle hydrodynamics,SPH)描述流场,利用牛顿−欧拉运动方程描述刚性颗粒的运动状态,在较宽的雷诺数范围内借助已有的实验和数值模拟结果对模型进行了验证,探讨了颗粒旋转、颗粒粒径、颗粒间距、颗粒形状(球形、椭球)、雷诺数对圆管泊肃叶流下中性浮力颗粒横向迁移最终稳定位置的影响。 2015年,Kim等[32]采用惩罚浸没边界方法(penalty immersed boundary method,PIBM)数值模拟了三维弹性胶囊在平面泊肃叶流下横向迁移的平衡位置受颗粒的初始横向位置、雷诺数、通道宽高比及流体黏度等的影响,然而缺少实验结果来验证数值模拟的准确性。 虽然一些学者对泊肃叶流下中性浮力颗粒的横向迁移特性进行了实验和数值模拟研究,但是,实验研究多关注颗粒迁移后最终稳定的横向位置,对颗粒迁移过程的研究存在明显不足。受实验测试手段的限制,通过实验研究难以获得颗粒动力学行为和颗粒周围流场的细节信息,因而也难以揭示颗粒横向迁移的内在机理。虽然多种数值模拟方法在颗粒横向迁移研究中得到应用,但是,数值模拟多针对二维平面泊肃叶流动下颗粒的横向迁移,对三维管道内颗粒横向迁移的研究相对较少。此外,针对高雷诺数时(Re>1000)圆管内颗粒横向迁移最终平衡位置的个数和位置的研究还存在不足,迫切需要对此开展三维圆管内颗粒横向迁移的全过程研究。现将借助开源流体−颗粒系统数值模拟软件CFDEMcoupling[33],基于DF/FD方法模拟再现圆管泊肃叶流下单个颗粒横向迁移行为,以期为今后通过数值模拟方法进行颗粒横向迁移的精细动力学行为及其内在机理研究提供基础。 针对三维水平圆管泊肃叶流下单个中性浮力颗粒的惯性迁移进行数值模拟研究,所研究液固两相系统的示意图如图5所示。L为管长,u为流体速度。 图5 数值模拟中液固两相系统示意图Fig.5 Schematic diagram of the liquid-solid two-phase system in numerical simulation 采用DF/FD方法进行数值模拟。首先,忽略颗粒的存在,整个区域都作为流体域计算;然后,计算流体对颗粒的作用力,将该力以体积力的形式包含到颗粒运动模型中;最后,为了满足守恒方程,对速度场和压力场进行了修正[34]。 管内流体的连续性方程和动量方程为[34-36] 式中:u为速度矢量;ρ为流体密度;p为流体压力;t为时间;μ为流体动力黏度。 采用牛顿−欧拉方法对单个中性浮力颗粒运动进行建模[34,36],则有 式中:m,I分别为颗粒的质量和转动惯量;v,ω分别为颗粒速度和角速度;Ff为颗粒受到的流体力;R为颗粒中心指向颗粒表面的矢量。 通过对颗粒的浸没边界受力进行积分以求解流体力Ff[34,36]。 式中,Ωs为颗粒边界。 在流固耦合计算过程中,首先通过动量方程(式(2))计算得到临时速度场,然后将颗粒的速度施加到临时速度场中,得到新速度场;为了满足连续性方程(式(1)),利用泊松方程修正新速度场,得到修正后的速度场;将修正后的速度场引入到动量方程中,对压力场进行修正[34,36]。 数值模拟时采用和Matas等[1]的实验相同的流体条件(ρ=1050 kg/m3,μ=1.52×10−3m2/s,平均流速U=0.0124 m/s)、颗粒参数(d=0.9 mm,密度与流体密度相同)及管径(D=8 mm)。 为了减少计算量,一方面,对进口和出口施加周期性边界条件,即从出口流出的流体和颗粒,以相同的速度从进口流入,采用更短的管长(L=100 mm)模拟管长较长的管内颗粒的行为[37];另一方面,网格划分时,采用静态网格和动态网格加密相结合的方法。具体网格划分方法:首先对整个计算区域划分静态网格(图6);计算过程中,对于流体与颗粒界面所在的静态网格进行动态网格加密(图7)。从而实现了对流固界面的精准描述,同时避免了全部采用静态网格时网格数目庞大的问题。 图6 数值模拟采用的静态网格Fig.6 Static mesh used in numerical simulation 图7 颗粒与流体界面的静态网格和动态网格Fig. 7 Static and dynamic meshes at particle-fluid boundary used in numerical simulation 数值模拟中,采用PISO算法求解流场。鉴于求解流场的时间步长应小于流体流经一个网格的时间,即满足库朗(Courant)数小于1;求解颗粒运动的时间步长应小于颗粒的松弛时间,结合流固耦合计算的特点,流场计算时间步长采用3×10−5s,颗粒计算时间步长采用3×10−6s。 数值模拟得到的远离颗粒位置(与颗粒的轴向间距大于10d)的管道横截面上流体速度曲线与泊肃叶流下流体速度的解析解的对比关系如图8所示,可见本文模拟得到的数值解和解析解吻合良好。u为当地流体的速度,umax为圆管内的最大速度。此外,从数值模拟结果可以看出,数值模拟和解析解得到的管道内流体的速度分布几乎完全重合,这表明建立的模型和计算方法能够准确描述泊肃叶流的流场特性。 图8 泊肃叶流速度分布数值解与解析解的对比Fig.8 Comparison between numerical and analytical solutions of the velocity profile in Poiseuille flow 图9给出了数值模拟得到的单个颗粒横向迁移随时间的变化关系,如果不考虑颗粒旋转(不考虑式(4)),仍能发生颗粒的横向迁移,无量纲初始位置r0/R=0.2,0.4,0.75时,颗粒最终稳定位置对应的r/R≈0.4,这与Matas等[1]的实验结果中颗粒横向迁移最终稳定的平衡位置r/R≈0.68仍有很大差异。在考虑颗粒旋转(增加式(4))后,数值模拟得到的颗粒横向迁移最终稳定的平衡位置r/R≈0.66,数值模拟与实验的相对误差小于3%。这表明在颗粒惯性迁移研究中应当考虑颗粒的旋转。考虑旋转时颗粒横向迁移的平衡位置更接近壁面的原因是:颗粒运动对流体产生影响的距离对颗粒迁移的平衡位置起重要作用,该距离越大,颗粒越靠近壁面;旋转颗粒运动比不旋转颗粒运动对流体产生影响的距离更大,使得颗粒迁移的平衡位置更接近壁面。图9的结果还表明,本文的模型和数值模拟方法能够准确预测圆管泊肃叶流下中性浮力颗粒的横向迁移。 图9 数值模拟得到的颗粒横向迁移随时间的变化关系Fig.9 Lateral migration of the particle as a function of time obtained from numerical simulation 随着微流控技术的发展,管道内颗粒横向迁移现象成为研究热点,一些学者针对泊肃叶流下中性浮力颗粒的横向迁移开展了实验与数值模拟研究。然而,已有实验研究主要集中在对不同条件下颗粒横向迁移最终稳定平衡位置的研究,受限于微尺度条件下的测量手段,单纯依靠实验研究难以展示颗粒横向迁移的全过程及其内在机理。数值模拟方法易于改变参数,便于获取流场和颗粒动力学特性的详细信息,在揭示两相流现象及机理上具有实验研究难以比拟的优点。目前,有限元方法、虚拟区域方法、格子波尔兹曼方法、界面追踪方法等先后被用于研究泊肃叶流下颗粒横向迁移行为及机理。然而,由于颗粒横向迁移中流场和颗粒参数的复杂性,迄今对颗粒横向迁移行为的认识仍不够全面,甚至存在争议之处,对其内在机理的掌握还不够深入。鉴于上述原因,本文借助开源流体−颗粒系统数值模拟软件CFDEMcoupling,基于直接力/虚拟区域方法,开展泊肃叶流下单个中性浮力颗粒横向迁移的数值模拟,获得了准确的泊肃叶流场信息,展现了颗粒横向迁移的过程,为探究颗粒横向迁移动力学行为及机理提供了重要基础。在今后的研究中,应基于直接力/虚拟区域方法继续开展研究,以全面识别颗粒横向迁移的动力学行为,并揭示其内在机理,以期为颗粒横向迁移的实际应用提供科学依据和方法指导。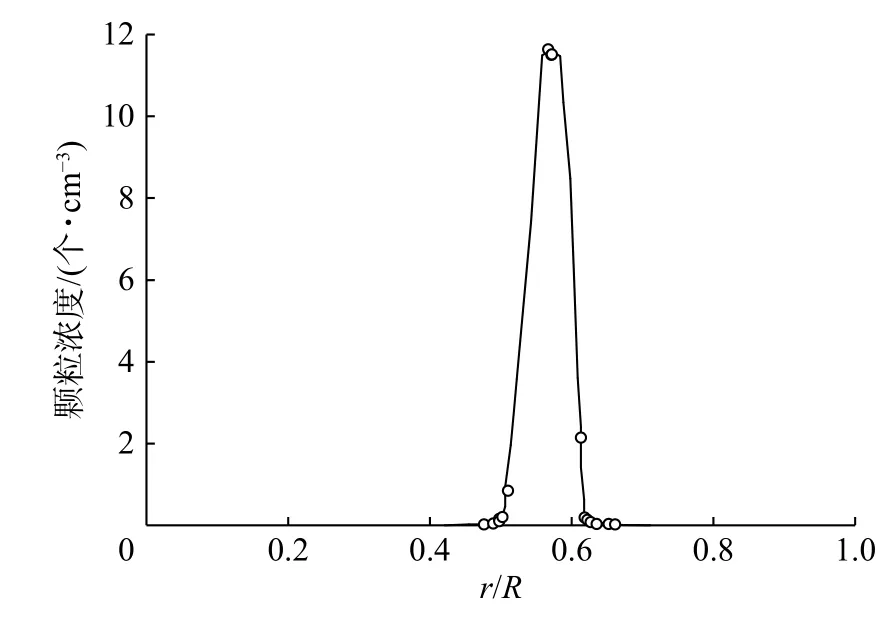

1.2 矩形与方形通道内的实验研究
1.3 其他相关研究
2 泊肃叶流下中性浮力颗粒横向迁移的数值模拟研究
2.1 有限元方法
2.2 虚拟区域方法
2.3 格子玻尔兹曼方法
2.4 界面追踪方法
2.5 其他方法
3 圆管泊肃叶流下中性浮力颗粒横向迁移的三维数值模拟
3.1 数学模型
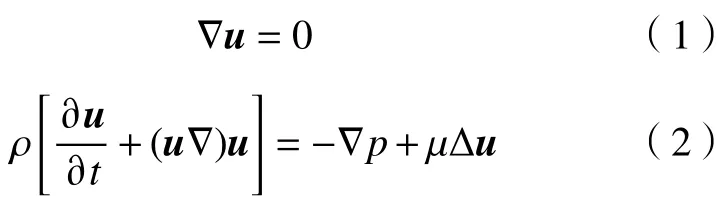

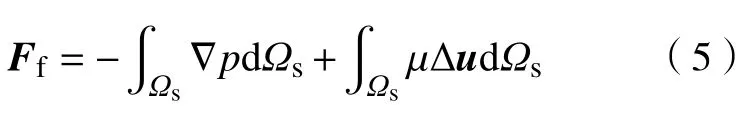
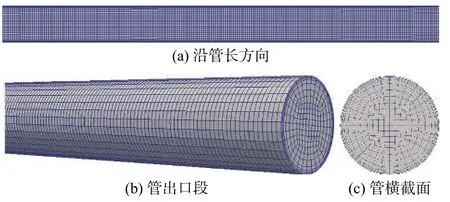
3.2 数值模拟条件和方法

3.3 泊肃叶流速度分布和颗粒横向迁移过程数值模拟结果

4 结束语

