无限大板功能梯度材料反平面裂纹问题的研究
郭昱彤,张雪霞,赵文彬,郭 璐
(太原科技大学 应用科学学院,太原 030024)
近几年,对功能梯度材料的研究成了热门。因为该材料的非均匀性,它可以消除传统复合材料的缺陷。因此,它可以应用到各个领域,如能源,运输,光学,生物医学工程等[1-2]。
冯文杰[3]基于位错密度函数研究了正交各向异性功能梯度条中多个共线Griffith裂纹的反平面剪切冲击问题。Chen等人[4]假定带钢的上边缘是无牵引力的,下边是固定的,利用积分变换法,导出一个初等解并建立奇异积分方程,弹性分析了功能梯度材料反平面弹性共线裂纹问题。Zhang等人[5-7]利用解析法,探究了无穷大反平面裂纹问题。李永东[8]基于涂层圆柱形复合材料界面的断裂力学理论模型并用分离变量法研究了圆柱形复合材料的界面开裂问题。陆万顺等人[9]研究了层合板结构中的反平面运动裂纹问题并用copson方法求解。文献[10]研究了正交异性基板在移动裂纹作用下的动态行为,并采用非均匀涂层对其进行了增强。文献[11]讨论了主要断裂特征(应力强度因子和能量释放速率)对双材料常数的依赖关系的解析解和半解析解,给出了界面裂纹与内部裂纹相互作用的反平面剪切问题的详细表达式。
本文采用负指数幂模型,运用数值解析法,再通过转化,求解奇异积分方程的解,来获取应力强度因子的解析式。探讨相关参数对应力强度因子的影响。
1 材料物性参数的负指数幂模型
如图1是含裂纹长度为2a的功能梯度材料。x轴和y轴相互垂直,坐标y是自变量,切变模量μx,μy是因变量,而且μx,μy按如下变化。即剪切模量采用负指数幂模型:
模型:
μx(y)=(μx)0/(c+α|y|)k
μy(y)=(μy)0/(c+α|y|)k
(1)
其中c>0,α>0,k>0,剪切模量为(μx)0=μx(0)·ck和(μy)0=μy(0)·ck
应力-位移关系为:
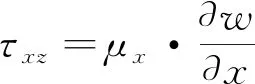
(2)
2 建立控制方程和边界条件
应力平衡方程:
(3)
将应力-位移关系(2)代入到应力平衡方程(3)得到控制方程为:
(4)
给出边界条件:
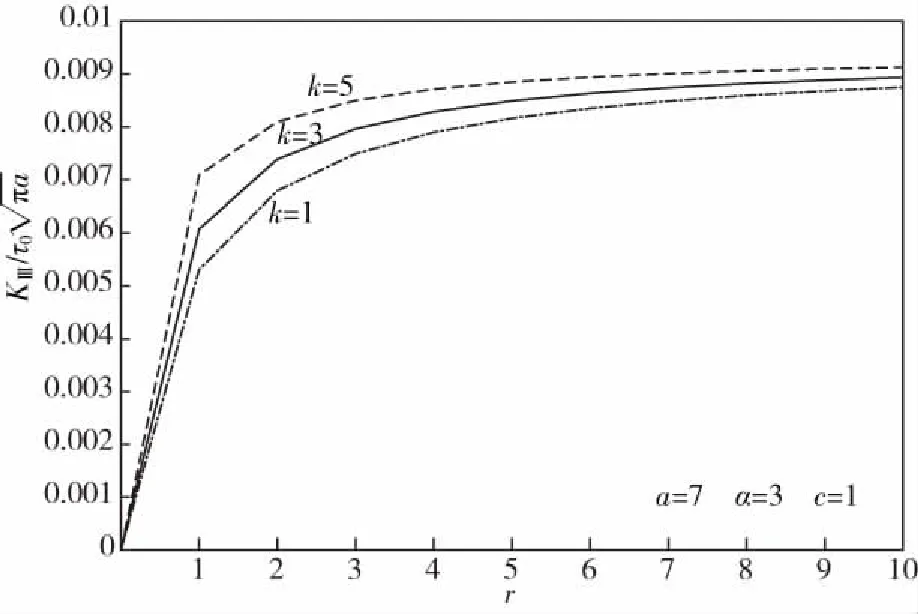
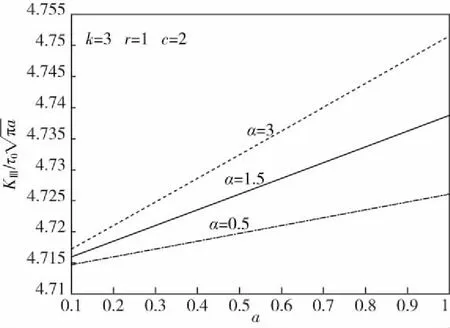
τyz(x,0)=-τ0|x| (5.1) w(x,0)=0 |x|≥a (5.2) 由于裂纹的对称性,只考虑x>0,y>0的平面,引入关于x的Fourier余弦变换 (6) (7) 设变量代换 (8) 可得到: (9) (10) 式(10)是标准的修正Bessel微分方程,由其解并考虑y→∞处的正则条件,方程(10)的解为: (11) 把式(11)代入到式(6),得到: Kβ[(c+αy)S/α]cos(sx)ds 把式(11)代入到式(2)得: Kβ[(c+αy)S/α]sin(sx)ds (12) [(c+αy)S/α]}cos(sx)ds (13) 由式(11)、式(13)以及边界条件(5.1)、(5.2),可得到一组对偶积分方程组(14) (14) (15) 采用copson方法求解对偶积分方程组(14),得其解: (16) 其中J0()是零阶第一类Bessel函数,函数Φ(ξ)由如下第二类Fredholm积分方程控制: (17) 通过数值积分方法,求解(17)可得到Φ(1)的数值解。 对(16)式进行分部积分,得到式(18): (18) τxz= [(c+αy)S/α]}cos(sx)ds= (19) 考虑到s→∞处上述应力积分表达式,将积分核较大的s值展开,并考虑x→∞时,Kβ(x)和Kβ′(x)的渐进性: (20) 定义复变量z1=x+iry,则有: (21) 这里的r1和θ1在图1中有定义。第一类一阶Bessel函数需满足: (22) 由式(19)-(22)得(23.1)-(23.2): (23.1) (23.2) 令x=r1cosθ1,y=r1sinθ1 (23.1)、(23.2)在r1→0处的变化情况,局部应力场如下: τyz(r1,θ1)= (24) τxz(r1,θ1)= (25) 符号说明:裂纹长度:2a;梯度参数:c,α,k;不均匀系数:r取2a=14 mm,c=1,α=3,在k=1,3,5时,讨论了标准应力强度因子与不均匀系数r之间的的变化关系,如图2.由图知,当给定a、α、c一定时,k,r与应力强度因子处于正相关。 图2 不均匀系数r和梯度参数k对应力强度因子的影响Fig.2 The effect of inhomogenous coefficient r and gradient parameter k on the stress intensity 取k=3,r=1,α=1,在2a=0.4,1,2.4 mm时,探究应力强度因子与梯度参数c的关系,如图3.由图知,当r、α、k一定时,a与应力强度因子处于正相关,c与应力强度因子处于负相关。 图3 梯度参数c和裂纹长度a对应力强度因子的影响Fig.3 The effect ofgradient parameter c and crack length a on the stress intensity 取k=3,r=1,c=2,在α=0.5,1.5,3时,研究了a对标准应力强度因子的影响,如图4.由图知,在r、c、k一定时,a,α与应力强度因子处于正相关,这一点与胡志新文章中的结论相同[12]。 图4 裂纹长度a和梯度参数α对应力强度因子的影响Fig.4 The effect ofcrack length a and gradient parameter α on the stress intensity factor 探究无限大板功能梯度材料的反平面静态裂纹问题。通过解析法将问题化为第二类Fredholm积分方程,分析了相关参数与应力强度因子之间的变化关系。结果说明:控制梯度参数与正交于裂纹面的切变模量可以控制裂纹扩展。3 导出对偶积分方程
4 裂纹尖端应力场及应力强度因子
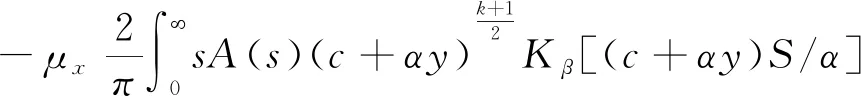



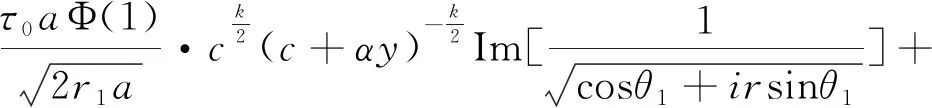
5 数值模拟

6 总结

