杉木木材酸性染料染色工艺优化

邓邵平, 王春灿, 林金国,2, 饶久平

(1.福建农林大学材料工程学院；2.国家林业局杉木工程技术研究中心，福建 福州 350002)

木材染色是改善木材视觉特性、实现普通木材模拟珍贵树种木材的有效方法[1-3]，也是人工林木材高效利用的重要手段之一，在家具和装修中有较广泛的应用[4-5].但染色效果和染色过程密切相关，良好的工艺直接影响着染色材的品质，因此，染色工艺条件的优化备受重视.目前，单因素试验设计、正交试验设计等在木材染色过程中的应用已有许多报道[6-9].然而，由于评价木材染色效果的指标很多[10]，上述优化方法往往是对多因素单目标值进行分析评价，一般无法得到一致的优化结果，给染色工艺参数的确定带来困难.因此，有必要采用一种能对多指标正交试验结果进行综合评价的方法，使优化出的染色工艺参数更为客观和实际.

模糊数学综合评判方法[11]因能对受多个因素影响的多性能指标做出一个总体的评价，有利于获得较为客观与科学的评价结果而在很多领域得到应用[12-15]，近年来也逐渐应用于多指标正交试验[16-19].然而，目前模糊正交法应用于木材染色工艺优化的研究还鲜见报道.本文选择酸性大红3R对经冻融循环预处理后的人工林杉木木材[Cunninghamialanceolata(Lamb.) Hook]进行染色处理，采用正交试验考察染液质量分数、染色时间、染色温度和促染剂用量对木材染透率、上染率和色差的影响；通过极差分析和方差分析得到影响染透率、上染率和色差的主要因素；综合考虑各因素对3个指标的影响，运用模糊数学综合评判法对染色效果进行评价，进而优化杉木木材的染色工艺参数，达到高效利用杉木资源的目的.

1 材料与方法

1.1 供试材料

人工林杉木(树龄26～28年)无缺陷气干边材购自福建省南平市，尺寸为55 mm(长)×40 mm(宽)×12 mm(厚).酸性大红3R染料由天津裕华经济贸易总公司提供；无水硫酸钠(Na2SO4)为分析纯，由西陇化工股份有限公司提供.

1.2 主要仪器

HH-4型数显恒温水浴锅由上海梅香仪器有限公司提供；101-3ES型电热恒温鼓风干燥箱由上海科恒实业发展有限公司提供；HWS-150型恒温恒湿箱由上海精宏试验设备有限公司提供；PB-10型数显pH计由赛多利斯科学仪器(北京)有限公司提供；UV-3200型紫外可见分光光度计由上海美普达仪器有限公司提供；Color i7型测色配色仪由美国X-rite公司提供.

1.3 方法

1.3.1 木材预处理 染色前参照文献[20]对所有试材进行冻融循环预处理，干燥后调节含水率至12%左右备用.

1.3.2 试验设计 在单因素试验[21]基础上，固定浴比，选取染液质量分数(A)、染色时间(B)、温度(C)和促染剂用量(D)为主要影响因素(表1).选择L16(45)正交表设计试验，探讨染色工艺对染透率(Y1)、上染率(Y2)和表面色差(Y3)的影响，具体方案见表2.每组6块木材.参照王春灿等[21]的方法采用酸性大红3R染料对木材进行染色处理；染色后取出木材，用蒸馏水淋洗表面浮色；试材沥干后再经气干，测定Y1、Y2和Y3.

1.3.3 染透率 参照文献[20]的方法测定.

1.3.4 上染率 采用UV-3200型紫外可见分光光度计分别测定各染液染色前后最大吸收波长处的光密度.同一染液移2次，每次测3遍，结果取6次平均值.用下式计算上染率：

(1)

式中：Y1为上染率(%)；A0和A1分别为染色前染液的光密度和残液的光密度.

1.3.5 表面色差 采用国际照明委员会CIE(1976)的L*a*b*表色系统计算色差[22]，用Color i7测色配色仪分别测定染色前后木材的明度指数L*、红绿指数a*和黄蓝指数b*.每个试样在其中一条对角线上等距离取3点测试，分别计算处理前后各色度指数变化，按下式计算表面色差Y3：

(2)

2 结果与分析

2.1 正交试验结果

染色处理后木材的染透率、上染率和色差的测定结果见表2，极差分析和方差分析结果见表3、4.

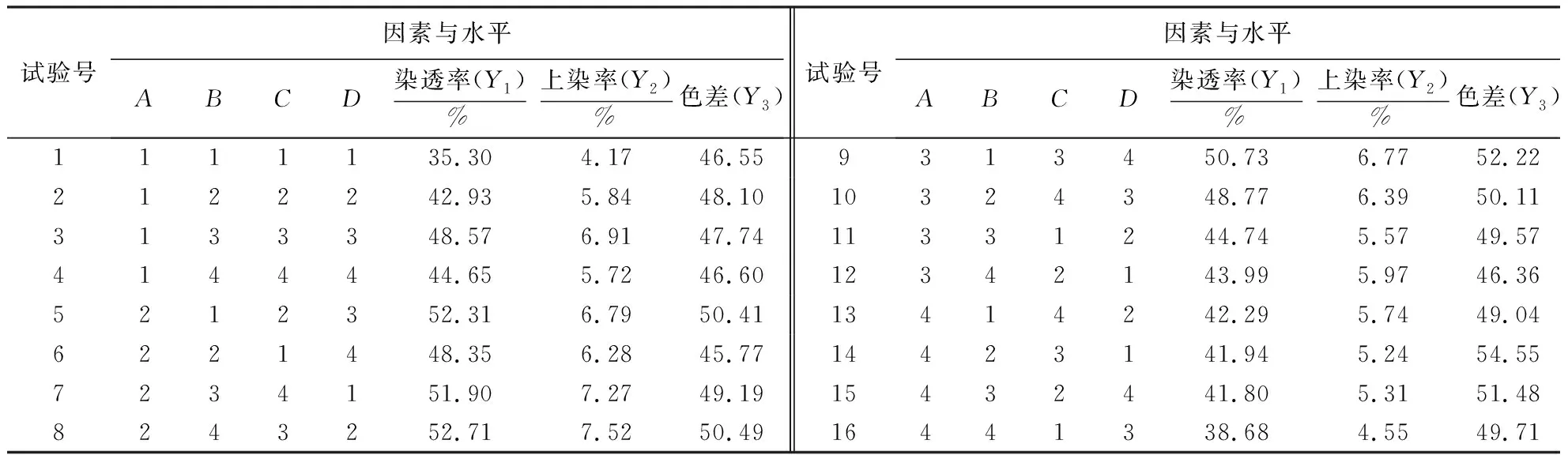
表2 正交试验方案与结果Table 2 Experiment design and results of the orthogonal test

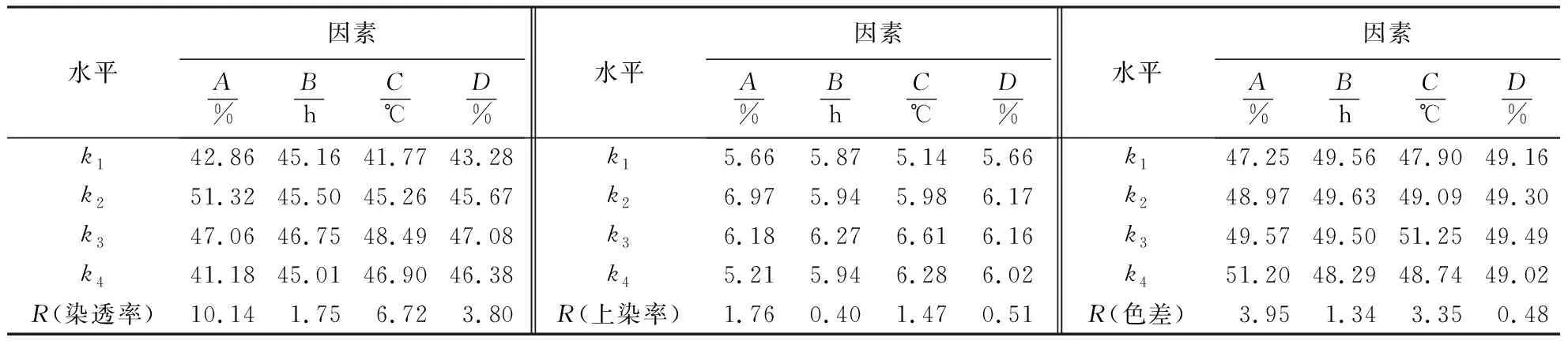
表3 极差分析1)Table 3 Range analysis of the dyeing properties of wood products

表4 方差分析结果1)Table 4 Variance analysis of the dyeing properties of wood products

由表3可知，各因素对染透率的影响程度表现为染液质量分数>染色温度>促染剂质量分数>染色时间，最优组合为A2B3C3D3；各因素对上染率的影响程度也表现为染液质量分数>染色温度>促染剂质量分数>染色时间，最优组合则为A2B3C3D2；各因素对色差的影响程度表现为染液质量分数>染色温度>染色时间>促染剂质量分数，最优组合为A4B2C3D3.

由表4可知，在显著性水平α=0.01下，染液质量分数对染透率的影响极显著，对染色温度的影响显著，其它因素则无显著影响；α=0.05时染液质量分数和染色温度对上染率的影响均显著，其它因素的影响不显著；α=0.10时各因素对色差均无显著影响.可见，对涉及多指标评价的木材染色，仅对单项指标进行评价无法得到一致的优化工艺组合.因此，需借鉴模糊综合评判法对染透率、上染率和色差进行综合评价，根据评价值优化木材的染色工艺参数.

2.2 模糊综合评判优选结果

2.2.1 评判矩阵的建立及结果 模糊综合评判矩阵由隶属函数计算的隶属度值确定[18].首先按模糊数学择大为优原则，利用建立的隶属函数式[17,19]对木材的染透率、上染率和色差的实测值进行转换，使各指标值模糊化.转换值按式(3)计算，结果见表5.

(3)

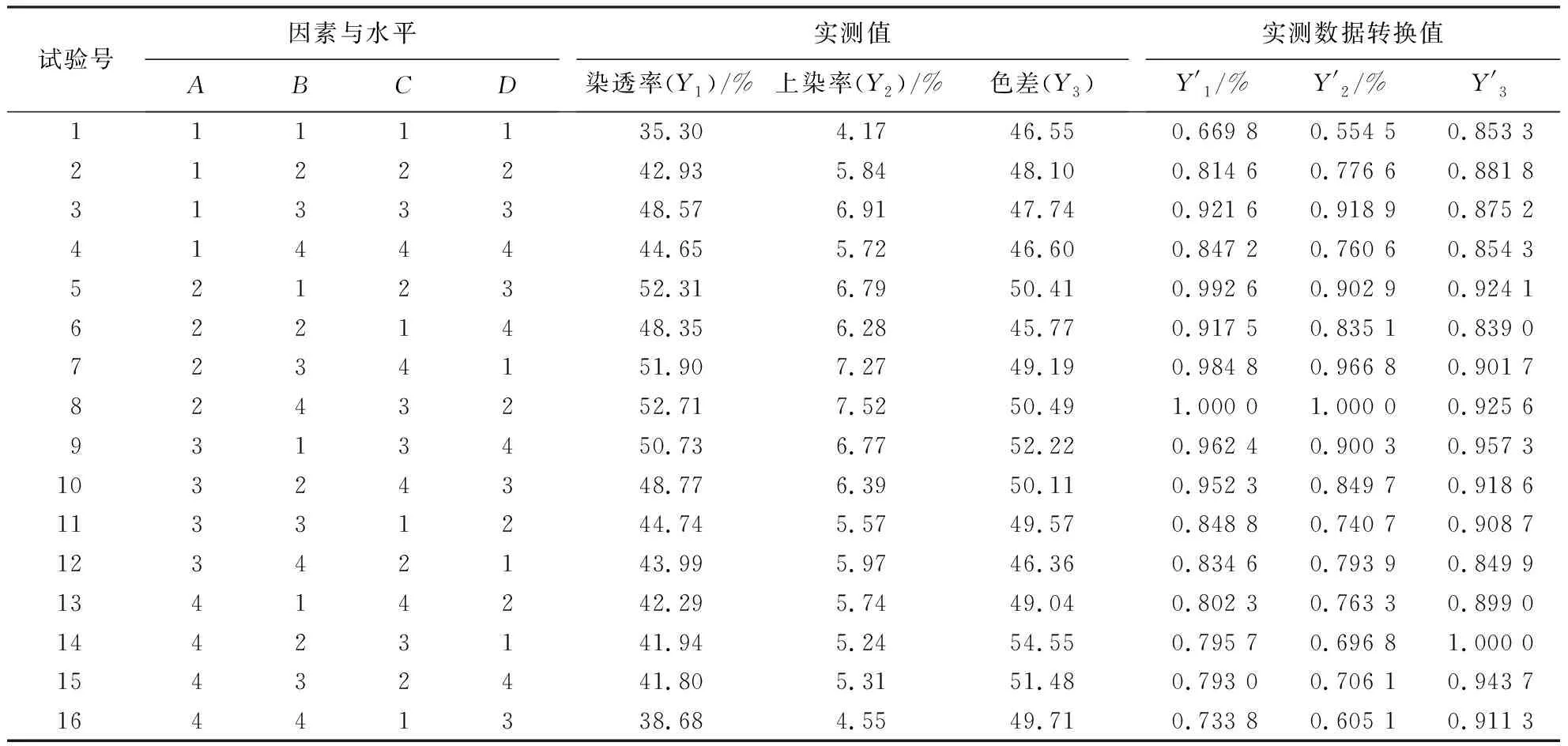
表5 正交试验各指标模糊转换结果Table 5 Fuzzy transform results of dye penetration rate, dye uptake rate and color difference

然后计算各因素各水平对应各指标转换值的水平均值，将各指标转换值映射到[0 1]区间，使各水平均值模糊化[14,16].

参照文献[14]的方法，将4个因素关于3个指标的总评语分别用模糊评价矩阵R1、R2、R3和R4表示，则r11、r12、r13和r14构成了模糊评判矩阵R1的第一行.依上述步骤分别对染液质量分数4个水平对应的上染率和色差转换值进行处理，其结果分别为矩阵R1的第2行和第3行.同理可得到其它3个因素对应的模糊评价矩阵，分别表示如下：

2.2.2 权重分配 权重是指各指标对评价对象的影响程度.进行模糊综合评判时，需对各指标的权重进行确定，目前常用的方法有Delphi、层次分析法和专家评分法等.本文采用专家评分法确定的染透率、上染率和色差的权重分别为0.300 0、0.300 0和0.400 0，并参照文献[23]计算熵值法权重，得到评价指标的权重系数分别0.313 7、0.285 1和0.401 2，即权重向量W=(0.313 7，0.285 1，0.401 2).

2.2.3 综合评判和水平优选 应用综合评判模型M(∧，∨)，将权重向量W与模糊矩阵R相乘[24]，即B=W·R，可得综合评判向量B={b1，b2，b3，b4}；归一化处理后得到B1～B4，即为各因素3个指标的综合评价结果，分别表示如下：

从综合评价结果可知，B1中水平2最大，根据最大为优原则，即染液质量分数2%时，染色效果最好；同理，得到染色时间、染色温度和促染剂质量分数的最优水平均为水平3，分别为4 h、90 ℃和3.0%，即最佳染色工艺参数组合为A2B3C3D3.

2.2.4 染色工艺条件的优化和验证 通过对染透率、上染率和色差的模糊数学综合评判，得到杉木木材的最佳染色工艺参数，即染液质量分数2.0%，染色时间4 h，染色温度90 ℃，促染剂质量分数3.0%.在此条件下进行4次染色验证，得到的染透率、上染率和色差的最大值分别为53.64%、7.59%和53.20，总体高于正交试验各指标的实测值，说明优化工艺合理、有效.

3 小结

利用酸性大红3R染色杉木木材，通过极差分析和方差分析考察染液质量分数、染色温度、促染剂质量分数和染色时间4个因素，结果表明染液质量分数和染色温度对染透率和上染率的影响显著；对于染透率，最优工艺组合为A2B3C3D3；对于上染率，最优组合为A2B3C3D2；对于色差，最优组合为A4B2C3D3.表明各指标单独优化时优化结果不一致.应用模糊数学综合评判法对染透率、上染率和色差进行综合评价，得出木材的最佳染色工艺参数组合为A2B3C3D3，即染液质量分数为2.0%，染色时间4 h，染色温度90 ℃，促染剂用量3.0%.在该条件下染色，染透率、上染率和色差分别可达53.64%、7.59%和53.20，总体高于正交试验各指标实测值，说明优化工艺合理有效.