电动汽车LCL复合型无线充电研究

（三峡大学电气与新能源学院，湖北 宜昌 443002）

在全球环境与能源问题的双重打击下，电动汽车的出现与迅速发展是解决这一问题的有效途径，国内外电动汽车的产量与销量也直追传统燃油汽车。无线充电早期风靡于智能手机，近些年，为了满足大量电动汽车充电需求，无线充电于电动汽车方面的研究也进行地如火如荼[1-5]。电动汽车可以通过换电站电池更换，有线、无线充电进行电能的补给。电池更换需要建设大量换电站，且换电站需存储各种类型、品牌的电池，建造与运维成本较高；由于有线充电需要经常拔插插头，与插座存在物理磨损，易造成磨损部分老化，产生电火花，严重时甚至漏电，引起触电火灾等事故，并且恶劣环境下安全系数非常低[6]；因此，与电池更换和有线充电相比，无线充电方式采用非接触式充电，安全系数高，建设成本较电池更换低，是未来电动汽车电能补给的重要组成部分与趋势[7]。

电动汽车的核心部位为其动力来源—电池，目前通常采用Li（锂）电池。对Li电池充电时，首先为恒流模式，此时电流为恒定值，电池端电压缓慢升高，当达到额定值时，切换为恒压模式，期间充电电流不断下降至电池满电，充电结束，即广为人知的“CC-CV”模式。现实生活中，常常会因为车主或其他因素导致发射端与接收端线圈未完美对应，易导致耦合系数降低，影响充电效率。文献[8]采用相应控制方法来稳定输出电压，但是其控制方法与策略异常繁琐，消耗大量时间。

文 献 [9]将 MERS（magnetic energy recovery swith）使用于原边补偿结构，当耦合系数降低时以此使系统保证最大功率输出。文献[10-11]分别采用S-S与LCL-LCL拓扑结构，将额外的补偿电容和开关加入到原边网络，实现了CC与CV的随意切换，但需要发射端与接收端有良好的信息交换，高频磁场空间中易造成无线通信不稳定，且难以维持磁耦合谐振状态。

基于上述文献所存在的问题，文章建立LCL复合型新型结构，对副边线圈中的3个可变补偿电容的MERS的导通角进行控制，实现了在保证系统磁耦合谐振[12]的状态下，切换负载时系统也能稳定工作于CC，CV，MP 3种工作状态。相对于传统的无线充电系统，其优势在于电能传输更加稳定、高效，充电状态切换平滑，对于目前电动汽车无线充电发展有着重要推动作用。

1 系统特性分析

LCL复合型无线电能传输系统（radio energy transmission system，RETS）模型[13-15]如图1所示。

图1 LCL复合型无线电能传输系统模型Fig.1 Model of LCL-composite wireless power transmission system

图1中U1为交流电压源；Q1～Q4构成电压型逆变器；L10，C10分别为发射端补偿电感、补偿电容；LP，LS分别为原、副边线圈电感；MPS为线圈互感系数；L20为接收端补偿电感；Ck1，Ck2，Ck3为接收端 3个可变补偿电容；RL为电池负载等效电阻。文中副边结构使用了3个可变补偿电容，为了便于理论分析，将系统简化为图2，其中U2为高频交流电。

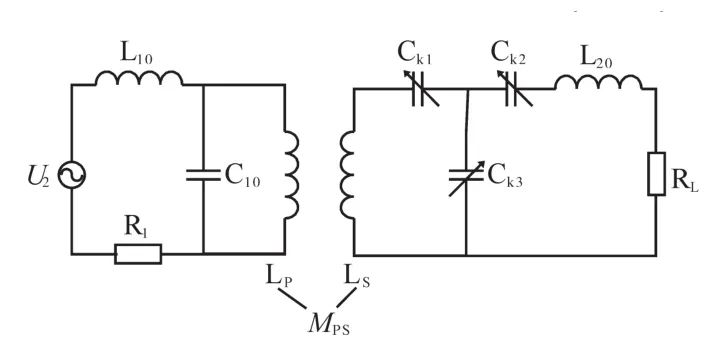
图2 LCL复合型简化电路Fig.2 LCL-composite simplified circuit

1.1 原边电路谐振分析

对于原边线圈，考虑到LCL型拓扑能使发射线圈的电流呈现出恒流源特性[16]，所以选择LCL结构。根据经典电路理论：

式中：ω为角频率。

可以取L10=LP，所以得到原边电路磁耦合谐振的条件为

1.2 副边电路谐振分析

从图2可以看到副边电路的结构相对复杂，同理可得：

式中：RX为纯电阻。

由于Ck1，Ck2，Ck3为可变电容，所以副边线圈磁耦合谐振的条件为

2 CC，CV，MP状态特性分析

为了方便对3种状态的特性进行分析，将发射端电路等效为接收端的一个交流电源[17-19]，如图3所示，图3中Us为发射端等效到接收端的交流电压源。

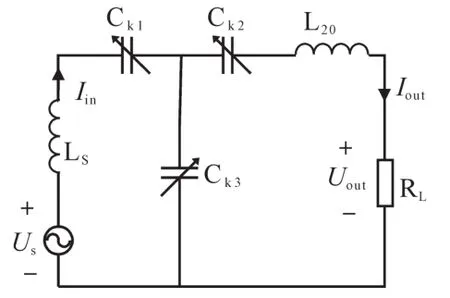
图3 副边线圈简化等效电路Fig.3 Simplified equivalent circuit of secondary coil

2.1 恒流输出原理

为简化计算，令β为一个常数，使得：

根据经典电路理论，由图3得：

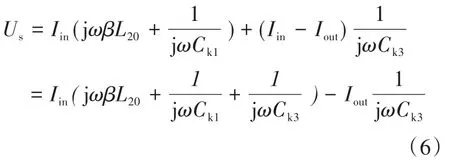
由式（6）可知，Iin的系数为0时，Iout仅与Ck3和Us有关，当Ck3为定值时，系统保持恒流输出。同时，系统需保证工作于磁耦合谐振状态，且其恒流条件也为耦合谐振条件，所以可以选择Ck1=Ck3，故当Ck3电容值确定时，可以得到：

由式（7）～式（9）可计算出LCL复合型RETS恒流输出时3个可变补偿电容的电容值。

2.2 恒压输出原理

由图3，有：

代入式（6），可得：

为了计算方便，令输入阻抗与输出阻抗分别为Zin和Zout：

根据经典电路理论有：

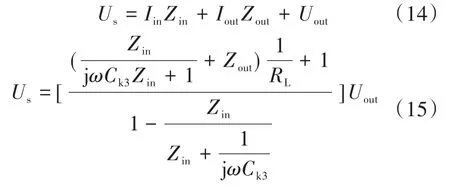
所以当1/RL前面的系数为0时，负载RL的电压Uout与自身无关。将式（12）、式（13）代入，可以得到在耦合谐振情况下的恒压输出的Ck1，Ck2，Ck3的电容值：

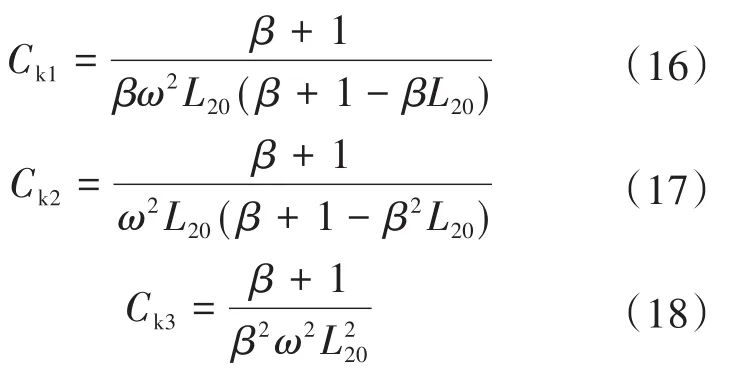
由式（16）～式（18）可计算出LCL复合型RETS恒压输出时3个可变补偿电容的电容值。

2.3 最大功率输出原理

在实际充电过程中，常常会因为车主或其他因素导致发射端与接收端线圈未完美对应，导致耦合系数降低，影响充电效率，系统无法维持最大功率输出。对存在于副边结构中的3个可变补偿电容的电容值进行切换匹配，不但能维持CC，CV模式，还可以实现维持最大功率输出模式[20-21]。当发射与接收线圈中存在障碍物，此时耦合系数骤降，充电效率极低，此时系统会有相应提示，对障碍物进行清理，以恢复正常。

系统最大传输功率条件为

式中：Zeq为等效阻抗；ZL*为负载阻抗的共轭值。所以当互感线圈的互感系数MPS发生变化时，为了维持磁耦合谐振状态，同时使系统实现恒定最大功率的条件为

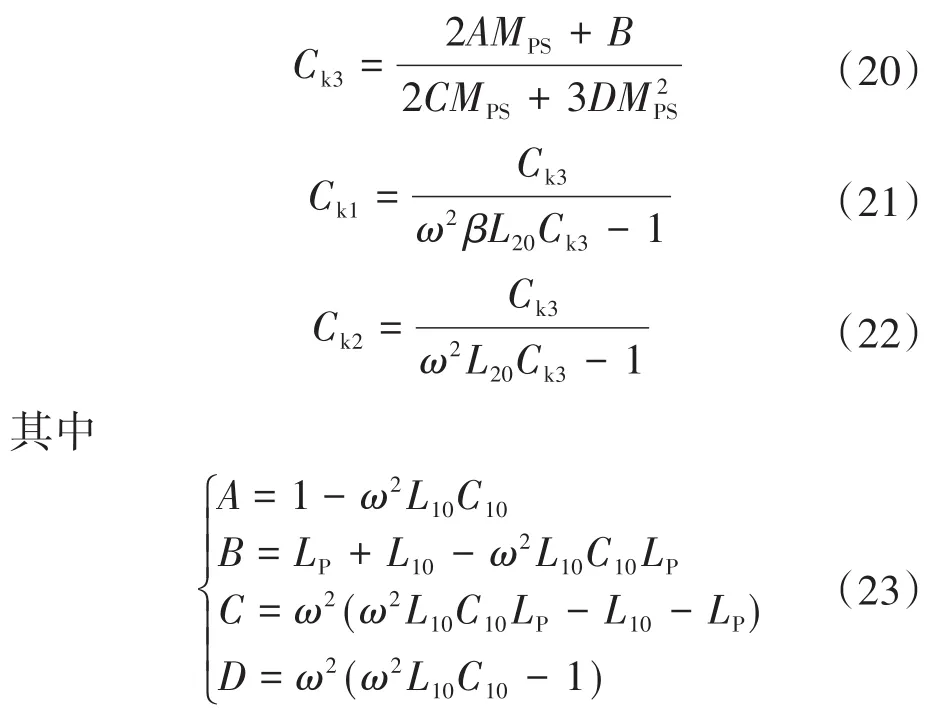
式（20）～式（22）表示了在其他网络参数保持不变的情况下，系统维持在最大功率输出时接收端3个可变补偿电容随MPS变化的电容值。

3 可变补偿电容分析

为了满足上述3种充电状态的切换，对副边结构中3个可变补偿电容采用MERS[22]控制，以此实现3个电容的动态调节。

3.1 MERS原理

全桥式MERS的电路如图4所示。

图4 MERS电路Fig.4 MERS circuit

由图4电路可知，若想实现MERS调节动态电容，只有导通MERS中的A，B，C，D其中一个MOSFET或者对角开关（A—D，B—C）导通，否则Cdc会被短路。根据不同的开关组合状态，MERS电路的工作状态也不同，详见表1。其中√代表导通，×代表关断[23]。

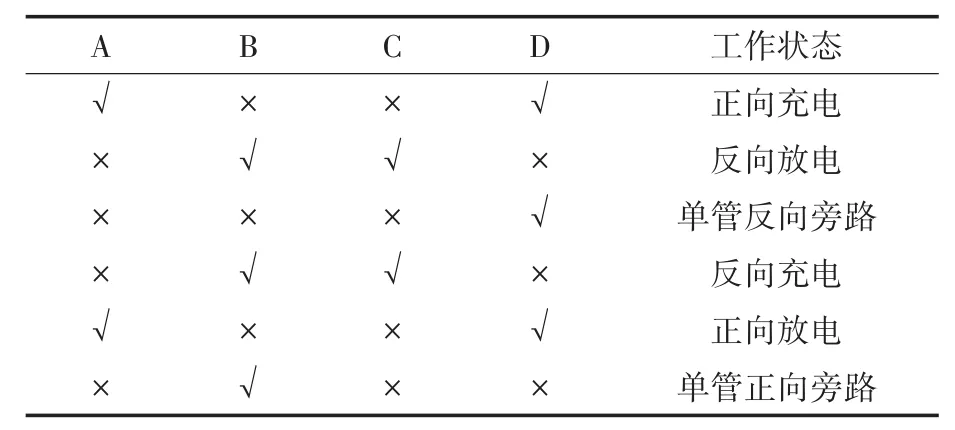
表1 MERS工作状态Tab.1 MERS working status

MERS电压输出波形如图5所示。将MERS运用于系统副边结构，任意一组双开关（如A—D）导通，Cdc进入充电模式；当Cdc两端电压为峰值时，即Cdc两端电压不会继续上升的时候，接着进行反向放电；放电结束后MERS则为单管反向旁路状态（只有一个MOSFET导通且与Cdc正向串联），此时Cdc上无电流；B—C导通，紧接着进入反向充电模式，直到Cdc两端电压为峰值；然后进行正向放电，MERS在放电结束后进入单管正向旁路状态，此刻Cdc上无电流。该过程即为MERS一个充放电周期，控制4个MOSFET的导通时刻，便能控制充放电过程，最终能达到MERS等效电容连续可控的效果。

3.2 MERS数学模型

采用移相控制调节MERS中MOSFET的开关导通时刻（时间周期转换为角度周期，即为α）来改变Cdc两端电压，从而实现等效电容的可调节性。由图5分析可知，在α=0°（图5中时间为0）时，MERS的电压波形为标准正弦波；当α≠0°时，在一个充放电周期中，MERS会有两次单管导通状态，该阶段Cdc不会有电流通过。

从上述可以得到MERS两端电压波形为图5所示。令XC为MERS中Cdc的容抗，C为等效电容值，i（x）为电流瞬时值，I为电流有效值，其电压值计算为

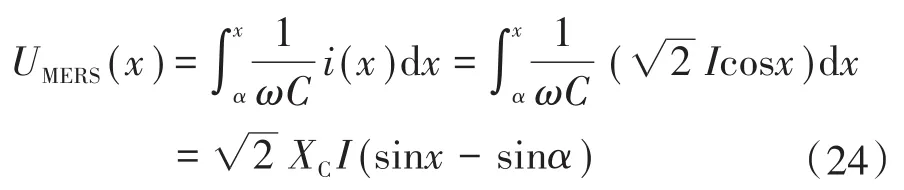
对式（24）进行傅里叶级数展开，取其基波项，整理得：

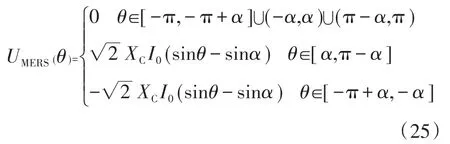
式中：I0为基波电流的有效值；θ为电压相位角。由此MERS基波电压的有效值和等效电容XMERS为

得到MERS的等效电容随导通角α变化曲线如图6所示。

图6 MERS电容曲线图Fig.6 MERS capacitance curve

通过式（26）和图6分析可得，相比于普通的电容，MERS通过控制MOSFET开关导通时刻，改变Cdc充放电状态，以此达到在单周期内得到一个“定值电容”。由式（27）可知，在Cdc电容值为一个定值的情况下，等效电容XMERS和导通角α关系见图6，只要改变导通角α，便能实现电容值的调整，由此来实现CC，CV，MP 3种工作状态。

4 仿真与实验验证

通过图5中MERS电压波形可知，当导通角α≠0°时，系统输出波形会发生一定程度的畸变。为了验证MERS是否适用于电动汽车无线充电系统，将分析输出谐波。对MERS施加380 V与220 V的电压，α与系统输出电流畸变率（THD）关系如图7所示。分析可知，随着α的增大，电流THD先增大至最大值后衰减至平稳，且明显380 V较220 V时电流THD更大。在端电压为220 V时，系统电流THD不会超过7%。

图7 电流畸变率变化图Fig.7 Variation of current distortion rate

对电容峰值电压进行分析，电容峰值电压随α变化的关系如图8所示，显而易见，随着α的增大，电容峰值电压也在增大，但在α＜40°时，其增幅较小，当α＞40°后，增幅较之前明显提高4倍以上。针对文章提出的系统，只要系统电压取220 V，合理设置网络参数，便能实现在CC，CV，MP3种状态下将3个MERS导通角α控制在40°（0.698 rad）以内，该种状态下，由MERS导致的输出畸变和电容峰值电压变化（整体最高为4.03%）便能忽略不计。

图8 电容峰值电压变化图Fig.8 Capacitance peak voltage variation diagram

参照图1搭建了LCL复合型结构无线电能传输装置的Simulink仿真模型来验证文章系统可行性，考虑到电磁影响以及电动汽车常用的无线传输频率，频率f选为13.56 kHz。电动汽车充电功率多为kW级，考虑到安全性，所以其模型参数选择如下：Us=220 V，MPS=28.27 μH，f=13.56 kHz，L20=24.22 μH，C0=3.54 pF，Ck1=15.76 nF，L10=26.39 μH，Ck2=25.13 nF，C10=10.44 pF，Ck3=15.76 nF，R1=50 Ω，CL=8.75 pF，LP=26.39 μH，L21=35.85 μH，LS=30.28 μH，RL=25～50 Ω。

当3个MERS的α分别为0°，18°，0°时，系统处于恒流输出状态，图9为其电流波形图。当RL=50 Ω时，系统开始充电直至稳定，此刻输出电流为6.713 A。将RL于0.001 s时切换为25 Ω，系统瞬间发生小幅度抖动，峰值电流为7.324 A，之后电流迅速稳定至6.718 A。切换RL前后电流变化率为0.07%，几乎可以忽略不计。

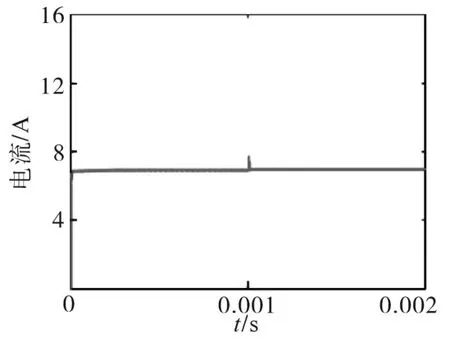
图9 CC模式系统输出电流波形Fig.9 Output current waveform of CC mode system

当3个MERS的α分别为37°，26.3°，18.9°时，系统处于恒压输出特性。该状态下的电压波形如图10所示。当RL=50 Ω时，系统开始充电直至稳定状态，此刻输出电压为180.56 V。将RL于0.001 s时切换为25 Ω，系统瞬间发生轻微波动，峰值电压为182.20 V，之后电压迅速稳定至177.95 V。切换RL前后电流变化率为1.45%，几乎可以忽略不计。

图10 CV模式系统输出电压波形Fig.10 Output voltage waveform of CV mode system

当互感MPS由28.27 μH逐渐减小时，副边采用定容量补偿的双LCL结构与文章系统的功率因数的变化作对比，如图11所示。前者随着MPS的减小，功率因数快速达到峰值0.81后，缓慢衰减至0.6。而本文系统，其功率因数基本维持在0.92左右。

图11 MPS变化时系统功率因数Fig.11 Power factor of system when MPS changes

通过上述的仿真结果可以得到在合理的参数设置下，控制3个MERS的α变化，系统便能有效地保持CC，CV，MP模式。并与文献[10]、文献[21]、文献[23]中3种模式的对比如表2所示。分析可得本文所提结构在CC，CV状态时的变化率明显低于其他3种模式，并且MP模式下功率因数最高且稳定。

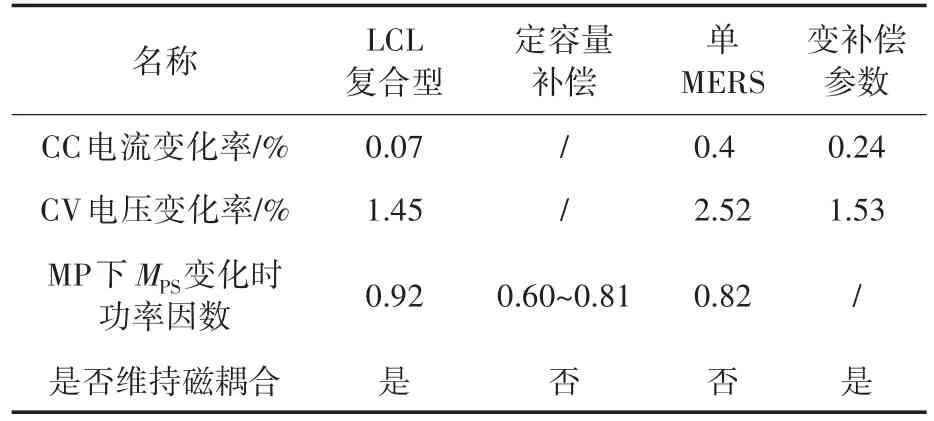
表2 数据分析对比Tab.2 Data analysis and comparison

依据前文仿真参数搭建了实验平台进行验证。参照仿真步骤，调整好参数，进行多次试验取平均值，对CC状态下，RL为50 Ω与25 Ω时的电流进行了测试记录，如图12与图13所示，分析可得，切换电阻前后电流基本稳定在6.36 A与6.41 A左右，相比仿真数据差距为5.26%与4.58%，实验平台上电流变化率为0.79%，结果较为理想。

图12 RL=50 Ω时的电流Fig.12 Current at RL=50 Ω

图13 RL=25 Ω时的电流Fig.13 Current at RL=25 Ω

对CV状态下，RL为50 Ω与25 Ω时的电压进行了测试记录，如图14与图15所示。分析可得，切换电阻前后电压基本稳定在172.0 V与168.2 V左右，相比仿真数据差距为4.74%与5.47%，实验平台上电压变化率为2.24%，结果较为理想。将两线圈位置进行水平横移，对功率因数进行计算统计，结果如图16所示，分析可得，在互感系数发生变化时，该系统功率因数稳定在0.88左右，相比仿真数据差距为4.35%，结果较为理想。

图14 RL=50 Ω时的电压Fig.14 Voltage at RL=50 Ω

图15 RL=25 Ω时的电压Fig.15 Voltage at RL=25 Ω

图16 线圈偏移时的功率因数Fig.16 Power factor at coil offset

由实验平台上得出的上述实验数据可以看出，在一些不可控的外界条件影响和实际操作存在误差的情况下，3种状态下，CC模式与仿真差距为5.45%左右，CV模式与仿真差距为5.59%左右，MP模式与仿真差距为4.35%。装置整体表现良好。

5 结论

文章提出了一种LCL复合型磁耦合谐振式无线充电系统，该系统副边存在3个由MERS控制的补偿电容。

分析了CC，CV，MP3种状态下3个补偿电容的状态，通过对3个MERS导通角的控制，使得系统能实现3种工作状态。

对MERS的数学模型进行了分析，验证了其可等效为动态电容，寻找出了等效电容值与导通角的关系，通过相关计算能得到3种状态下3个补偿电容的电容值。

搭建了Simulink模型与实验平台，对系统进行了仿真与实验验证，由结果可以得到当采用LCL复合型结构时，合理设置参数，仿真环境下各个参数都优于其他3种结构，实验数据显示，CC模式下，仿真与实验差距为5.45%左右；CV模式下，差距为5.59%左右；MP模式下，功率因数差距为4.35%，充分证明了文章所提系统能有效实现CC，CV，MP 3种模式。