带有滞后补偿的改进型I—V下垂控制策略

（四川大学电气工程学院，四川 成都 610065）

微电网是实现新能源并网的有效途径之一，已引起了国内外学者的普遍关注。微电网按供电形式可分为直流微电网和交流微电网2种，相比于交流微电网，直流微电网在运行和控制上具有如下优势[1]：1）直流微电网使用变流器较少，降低了系统损耗并且无需考虑频率问题；2）能量的控制只取决于直流母线电压；3）电网中的直流负荷越来越多，直流微电网能更好地为用户提供方便快捷的直流电源，准确地把握到负荷的发展趋势。因此，直流微电网已成为微电网技术发展的主要方向[1-3]。

典型的直流微电网系统结构如图1所示，其由交流电网、分布式电源、储能单元和负荷四部分组成。图1中，虚线框部分的双向DC-DC变换器是储能单元与直流母线进行能量交换的重要环节。由于直流微电网配备有多个相互并联的储能单元，因此功率的分配成为能量管理的主要问题。

图1 典型的直流微电网系统结构图Fig.1 Typical configuration of a DC microgrid

目前，下垂控制方式是直流微电网中并联变换器实现功率均分的主要方式[4]。文献[5]提出了直流微电网的分层控制策略，将控制分为3层：第1层为下垂控制，实现功率均分；第2层为补偿控制，实现对下垂控制所产生电压偏差的补偿；第3层控制调节直流微网各个部分的功率流动。文献[6-14]中，直流微电网的多并联DC-DC变换器对储能单元进行充放电控制时，均使用传统的V—I下垂控制，实现功率均分。

传统的V—I下垂控制方法是在“电流内环-电压外环”双闭环的基础上，在电压外环添加带有虚拟阻抗的输出电流反馈，以实现功率均分。文献[15-16]中，并联变换器采用I—V下垂控制策略实现功率均分；在这种控制方法中，通过输出电压参考值、虚拟阻抗与输出电流的数学关系计算得到电流的参考值，代替V—I下垂控制策略的电压PI控制环，实现功率均分；I—V下垂控制策略相较于传统的V—I下垂控制策略少用1个PI控制器，实现方式简单，响应速度更快。

但是，I—V下垂控制会引起变换器启动时超调量过大。这种超调量是由于启动时，参考电压与实际电压相差过大引起的，一般可以通过对电压控制器的输出进行限制来减小超调。本文提出一种带有滞后补偿的改进型I—V下垂控制方法来减小启动时的超调量。改进的滞后补偿器并不会完全消除稳态误差，也会产生下垂控制的电压偏差，以达到功率均衡的目的，同时，滞后补偿器减小电压外环的带宽，消除了启动过程中的超调量，对I—V下垂控制进行优化。

为分析所提控制方法的正确性和优越性，首先建立DC-DC变换器的平均状态模型，通过小信号建模，研究3种下垂控制策略下变换器的稳定裕量和闭环带宽，对3种控制方式下的稳定性进行对比，最后通过实验对所提算法进行验证。

1 DC-DC变换器建模

将直流微电网中连接储能单元的DC-DC变换器单独取出，用直流电源代替直流母线为变换器供电，用电阻负载代替储能单元。DC-DC变换器的结构框图如图2所示。其中，us为直流电源，s1和s2为开关管，L为电感，RL为电感的寄生电阻，C为稳压电容，RC为电容的寄生电阻，R为负载电阻，iL为电感电流，uC为电容电压，io和uo分别为输出电流和输出电压。

图2 DC-DC变换器结构框图Fig.2 The block diagram of the structure for DC-DC convertor

DC-DC变换器的状态空间平均模型为

式中：x为状态变量；u为输入变量；d为开关管s1的占空比；A，B分别为系数矩阵。

将状态空间平均方程线性化，加入扰动量，进行拉普拉斯变换，求得电感电流iL到输出电压uo的传递函数Gvi（s）和占空比d到电感电流iL的传递函数Gid（s），分别为

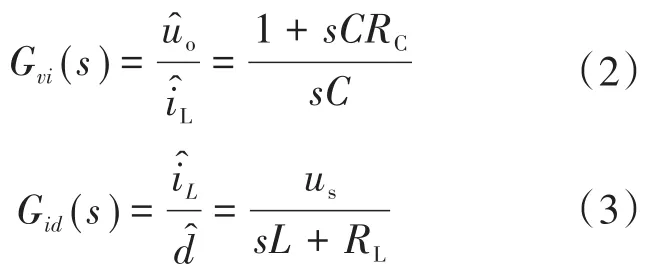
2 下垂控制策略

2.1 V—I下垂控制

在直流微电网中，传统的下垂控制方式是V—I下垂控制，通常采用“电流内环-电压外环”的双闭环，在电压外环上外加虚拟阻抗反馈回路的控制策略，控制结构框图如图3所示。

图3 V—I下垂控制结构框图Fig.3 The block diagram of structure for V—I droop control

图3中，uref为输出电压参考值；GPI_U（s）为电压外环比例积分（PI）控制器的传递函数；GPI_I（s）为电流内环PI控制器的传递函数；Gdealy=e-sTd为控制延时对应的传递函数，Td与采样周期Ts相等；Gm（s）为PWM脉冲调制器的传输延时对应的传递函数，Gm(s)=e-0.5sTd；Kdroop为下垂系数；uo为变换器的输出电压。

图4为电压—电流线性关系图。

图4 电压—电流线性关系图Fig.4 Linear relationship between voltage and current

由图4可知，Kdroop为电压电流线性关系的斜率，可表示如下：

式中：umin为输出电压允许偏差的最小值；imax为输出电流最大值。

变换器的输出电压可以表示为

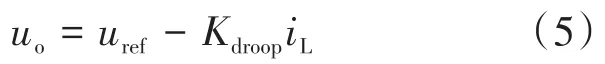
2.2 I—V下垂控制

直流微电网中另一种下垂控制方式是I—V下垂控制，通常采用电流内环，用电压、电流的线性关系求得内环电流的参考值，代替电压外环和下垂控制回路的控制策略，这种控制方式相较于传统的V—I下垂控制，少用了1个PI控制器，控制方法相对简单，控制结构框图如图5所示。图5中，k为比例系数。

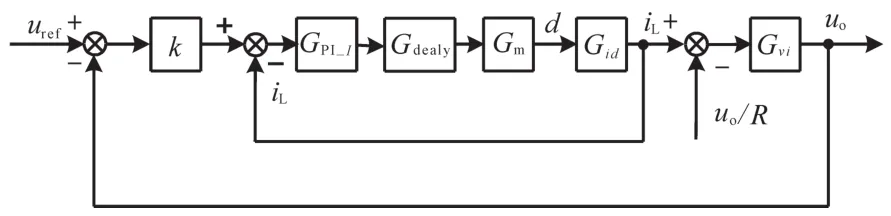
图5 I—V下垂控制结构框图Fig.5 The block diagram of the structure for I—V droop control

电流—电压的线性关系如图6所示，其中，uref为输出电压参考值，umin为输出电压允许偏差的最小值，imax为输出电流最大值。

图6 电流-电压线性关系图Fig.6 Linear relationship between current and voltage

由图6中电流—电压的线性关系可以求得电流i为

2.3 带有滞后补偿的改进型I—V下垂控制

I—V下垂控制利用电压电流之间比例关系代替电压外环PI控制和下垂控制回路，少用了1个PI控制器，简化了控制方式，但是会在DC-DC变换器启动时引起较大的超调量。为了消除这种启动的过大超调量，在控制算法中加入滞后补偿器。所提算法无需加入限幅器，达到消除超调的目的，其控制结构框图如图7所示。

图7 带有滞后补偿的I—V下垂控制结构框图Fig.7 The block diagram of the structure for I—V droop control with lag compensator

图7中，Gc（s）为改进后带有滞后补偿器的电压控制环，可以表示为

式中：k由式（6）可得，为滞后补偿器的增益；ωz和ωp分别为在紧靠原点附近添加的一对开环零点z和极点p所在的角频率，其中极点在零点的右侧。

与传统的滞后补偿器不同的是，传统的滞后补偿器由零极点分布控制增益和带宽，而本文所用的Gc（s）补偿器仅由系数k提供增益，由ωz和ωp控制带宽。

3 下垂控制策略性能分析

本文从输出电压的开环传递函数得到伯德图的稳定裕量，以及电流内环和电压外环闭环传递函数的带宽两个方面对3种下垂控制的性能进行对比分析，其中，3种下垂控制方法电流内环的PI控制器采用同一组参数。

DC-DC变换器电路参数设置如下：输入电压us=100 V；输出电压参考值uref=50 V；电感L=3 mH；电感电阻RL=0.01 Ω；电容C=2 000 μF；电容电阻RC=0.03 Ω；负载电阻R=10 Ω。DC-DC变换器控制参数设置如下：开关频率fs=10 kHz；电流环比例系数kp_i=0.15；电流环积分系数ki_i=80；电压环比例系数kp_u=69.6；电压环积分系数ki_u=101.4；归一化参数k1=0.02，k2=0.2；下垂系数Kdroop=0.1；补偿器零点频率ωz=250 rad/s；补偿器极点频率ωp=20 rad/s。

3.1 V—I下垂控制

由图3可得，DC-DC变换器电流内环的闭环传递函数Gi(s)表示为

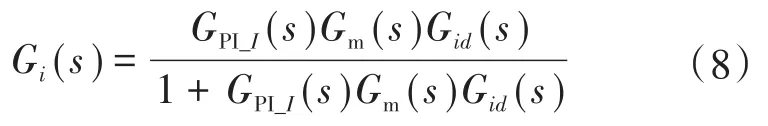
将前文设置的参数代入式（8）中，绘制出电流内环的闭环幅频和相频特性曲线如图8所示。由图8可得，在504 Hz时，幅值增益下降3 dB，电流内环的带宽为504 Hz。

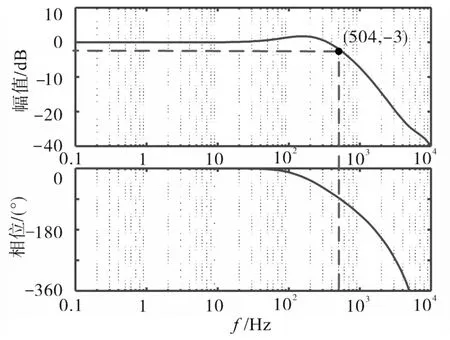
图8 电流内环闭环频率特性曲线（V—I）Fig.8 The frequency characteristic curves of inner current closed-loop（V—I）

DC-DC变换器电压外环的闭环传递函数Gv(s)表示为

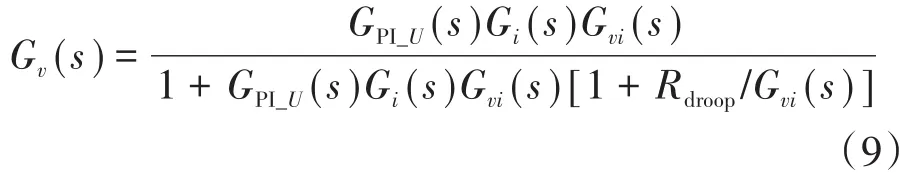
为求得DC-DC变换器电压外环的带宽，令电流内环闭环传递函数Gi()s=1，得到传递函数Gvb(s)：

将前文设置的参数代入式（10）中，绘制出电压环在Gi(s)=1时，闭环幅频和相频特性曲线如图9所示。

图9 电压外环闭环频率特性曲线（V—I）Fig.9 The frequency characteristic curves of outer voltage closed-loop（V—I）

由图9可得，在53.4 Hz时，幅值增益下降3 dB，电压外环的带宽为53.4 Hz。

DC-DC变换器输出电压uo的开环传递函数Gk(s)表示为

将前文设置的参数代入式（11）中，绘制出电压外环的开环幅频和相频特性曲线如图10所示。由图10可得，在61.4 Hz时，幅值增益穿越0 dB线，相角裕量为91.6°，系统稳定。

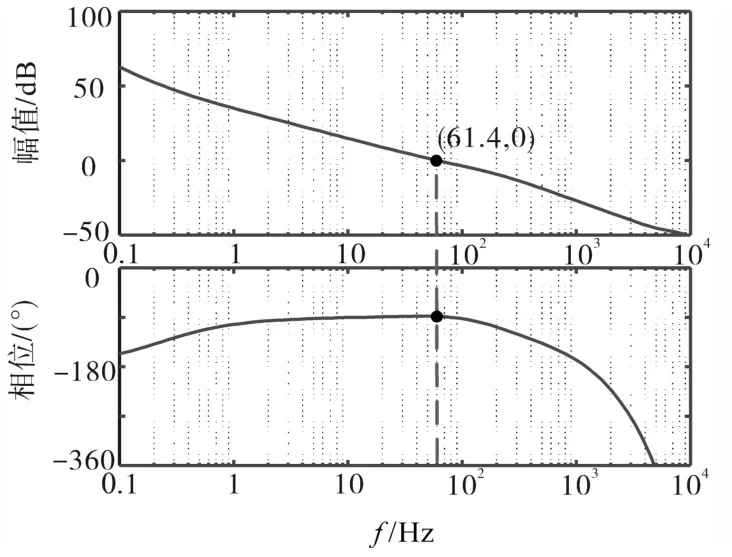
图10 电压外环开环频率特性曲线（V—I）Fig.10 The frequency characteristic curves of outer voltage open-loop（V—I）

3.2 I—V下垂控制

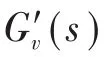
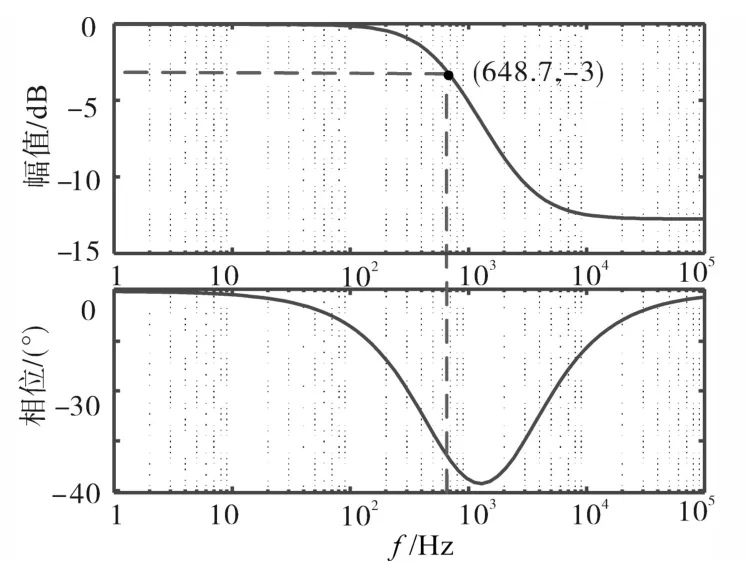
图11 电压外环闭环频率特性曲线（I—V）Fig.11 The frequency characteristic curves of outer voltage closed-loop（I—V）

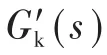
将前文中设置的参数代入式（14）中，绘制出电压外环的开环幅频和相频特性曲线如图12所示。由图12可得，在581.4 Hz时，幅值增益穿越0 dB线，相角裕量为6.5°时系统稳定，但稳定裕量很小。

图12 电压外环开环频率特性曲线（I—V）Fig.12 The frequency characteristic curves of outer voltage open-loop（I—V）

3.3 带有滞后补偿的改进型I—V下垂控制

图13 电压外环闭环频率特性曲线（改进I—V）Fig.13 The frequency characteristic curves of outer voltage closed-loop（improved I—V）

将参数代入式（17）中，绘制出电压外环的开环幅频和相频特性曲线如图14所示。由图14可得，在81.3 Hz时，幅值增益穿越0 dB线，相角裕量为60.4°，系统稳定。

图14 电压外环开环频率特性曲线（改进I—V）Fig.14 The frequency characteristic curves of outer voltage open-loop（improved I—V）

综上对3种下垂控制方式的带宽和稳定性分析，在电流内环完全相同的情况下，传统的V—I下垂控制方式的电压外环的带宽最小，约为54.3 Hz，但其具有最高的稳定性，稳定裕量约为91.6°；传统的I—V下垂控制下，虽然电压外环带宽最大，约为684.7 Hz，但其稳定性最差，稳定裕量约为6.5°；带有滞后补偿的I—V下垂控制下，电压外环的带宽相较于传统V—I下垂控制，由54.3 Hz增加到94.7 Hz，加快了系统的响应速度，系统的相角裕量相较于传统的I—V下垂控制，由6.5°增加到60.4°，提高了系统的稳定性。

4 实验验证

为了验证带有滞后补偿的DC-DC变换器I—V下垂控制策略的有效性，对所提算法进行了小功率实验测试，实验平台如图15所示，核心控制器为TMS320F28335。实验系统参数与第3节设置相同。

图15 样机实验平台Fig.15 Experiment setup of the prototype

图16为并联DC-DC变换器在传统V—I下垂控制下的输出电压电流动态实验波形。

图16 传统V—I下垂控制下电压电流动态实验波形Fig.16 Transient waveforms of uoand ioby the V—I droop control

由图16可知，在启动后约0.8 s后（t1处），输出电压uo稳定在49 V，电流io1稳定在4.7 A；在t2处，并入变换器2，输出电压uo阶跃到49.5 V，经过大约8 s，实现均流。在图中虚线框中，io1和io2在t2时刻都有电流突变，这是由于在并入变换器2前，变换器1已实现下垂控制，存在电压偏差，变换器2控制中，iL2为0，输出电压等于参考电压50 V，因此在并入变换器2的t2时刻，电流发生突变。

图17为并联DC-DC变换器在I—V下垂控制下，输出电压电流动态实验波形。

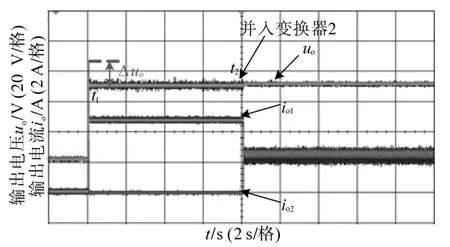
图17 I—V下垂控制下电压电流动态实验波形Fig.17 Transient waveforms of uoand ioby I—V droop control

由图17可知，在启动时刻，输出电压同时达到49 V稳定值，电流io1稳定在4.7 A左右，但是在启动时刻，存在较大超调量Δuo，图18为启动过程电压放大图。

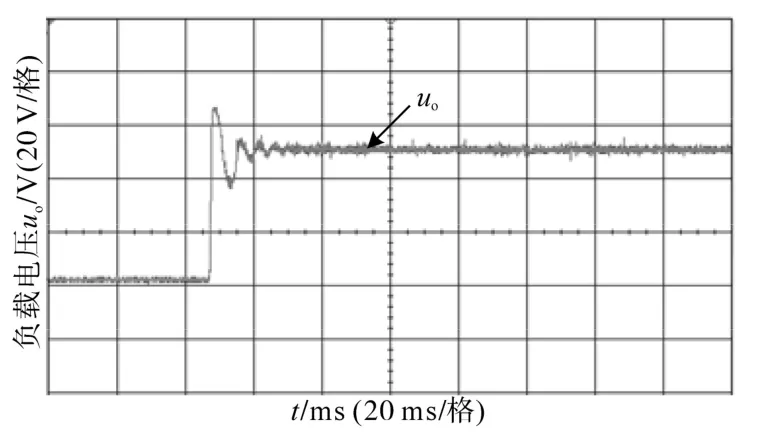
图18 I—V下垂控制下启动过程电压波形Fig.18 Transient waveforms of the start-up uoby I—V droop control

由图18可知，超调量超过20%；在t2时刻，并入变换器2，输出电压uo阶跃到49.5 V，同时完成均流；与图16相比可知，I—V下垂控制相比于传统的V—I下垂控制，响应速度很快，但在启动时产生较大的超调量，在并入变换器2后，虽然均流速度很快，但是明显电流波动更大，稳定性降低。

图19为并联DC-DC变换器在带有滞后补偿的I—V下垂控制下输出电压电流动态实验波形。

图19 改进的I—V下垂控制下电压电流动态实验波形Fig.19 Transient waveforms of uoand ioby improved I—V droop control

由图19可知，在启动后约0.3 s后（t1处），输出电压uo稳定在49 V，电流io1稳定在4.7 A；在t2时刻，并入变换器2，输出电压uo阶跃到49.5 V，经过大约50 ms，实现均流。与图16相比，系统的响应速度由0.8 s变为0.3 s，均流速度由8 s变为50 ms。与图17相比，在启动过程中不存在超调，在并入变换器2后，电流的波动明显减小，系统的稳定性明显提高，与理论分析一致。

5 结论

本文提出了带有滞后补偿的改进型I—V下垂控制策略，分析了所提算法响应速度及稳定性。相较于传统的控制策略，所提算法具有以下优点：

1）相比于传统的V—I下垂控制策略，所提算法在少用一个PI控制器的情况下，提高了系统的响应速度和均流速度，并有效地实现了功率的自动均衡。

2）相比于传统的I—V下垂控制策略，所提算法在消除过大的启动超调量、提高系统稳定性的同时，有效地实现了功率的自动均衡。