坐标概念的历史与椭圆方程的发展*

张 红 王 军

(四川师范大学数学科学学院 610068)

平面解析几何主要以圆锥曲线为中心内容，英国C.Smith(1844-1916)的Conic Sections本意为圆锥曲线，日本原滨吉将之译为解析几何学(1)(日)原滨吉.解析几何学讲义[M].东京：金刺芳流堂，1909：1,清末顾澄也译为解析几何学(2)(英)Smith原著，顾澄译补.高等教育解析几何学.第一册[M]，北京:北京作新社发行，1907：3.椭圆又是圆锥曲线的重要组成部分.从历史上看，圆锥曲线在教科书中有两种编排顺序：椭圆到双曲线再到抛物线，及抛物线到椭圆再到双曲线.清末民国时期，两种顺序均出现在我国的解析几何教科书中，但以后者为主.商务印书馆、中华书局等自编或翻译的多种教科书，其中圆锥曲线的编排顺序就是抛物线到椭圆再到双曲线.1949年以后人教版的高中教科书圆锥曲线的编排顺序采用前者，即椭圆到双曲线再到抛物线，并且教科书采用椭圆的第一定义，以此推导出椭圆的标准方程.本文以古希腊、中世纪、近现代为时间轴，讨论坐标雏形到坐标体系的完善过程，及椭圆定义从原始定义、第二定义、到第一定义的发展过程.在此基础上，分析了椭圆方程从文词叙述、符号引入到现代标准形式的演变过程.

1 坐标概念的起源与发展

“坐标系”是近代解析几何形成的基本要素.坐标概念经历了古希腊到近现代直至18世纪的漫长发展过程，在圆锥曲线的研究中，一直都扮演着重要角色.

1.1 坐标概念的雏形

坐标概念的雏形产生于古希腊以前，至于确切的开始，历史学家们持有不同的意见(3)Ruth M Tapper.coordinates in the histrory of mathematics[J]. Peoria:school science and mathematics.1929(7)：738—744.至少，坐标思想可以上溯到古埃及时期.埃及人采用划分地面区域的办法(4)梁宗巨.世界数学史·下册 [M].沈阳：辽宁教育出版社，2005:141，已经蕴含坐标概念的萌芽.希腊的希帕霍斯(Hipparchus，公元前180～125) 也曾用经度和纬度表示恒星在天球上的位置.古希腊学者一般采用圆锥曲线的直径、切线等表达坐标轴的概念.阿基米德(Archimedes, 约公元前287～212)曾用直径和切线表述椭圆的性质，阿波罗尼奥斯(Apollonious，约公元前262～公元前170)的《圆锥曲线论》中，相当于现在的“纵坐标”通常指的是直径末端的切线(5)Ruth M Tapper.coordinates in the histrory of mathematics[J]. Peoria:school science and mathematics.1929(7)：738—744.阿波罗尼奥斯甚至引用了两条正交直线(6)梁宗巨.世界数学史简编 [M].沈阳：辽宁人民出版社，1980:202，实际上已经意味了“坐标系”思想的萌芽.罗马时期的实际生活中，就出现了直角坐标和斜坐标的混合使用.罗马人在城市设计中，将罗马的城镇分布在两个轴线上.相比古希腊时期无意识地使用坐标，罗马时期实际上是有意识的运用了坐标思想(7)Ruth M Tapper.coordinates in the histrory of mathematics[J]. Peoria:school science and mathematics.1929(7)：738—744.

1.2 坐标概念的形成

从古希腊到中世纪，坐标概念取得了显著的进展.十四世纪，法国数学家奥雷姆(Oresme，1320～1382)不仅将经度和纬度分别对应纵坐标和横坐标，并用系统化的术语和部分广义的形式开始定义直角坐标系(8)Ruth M Tapper.coordinates in the histrory of mathematics[J]. Peoria:school science and mathematics,1929(7)：738—744.他所陈述的坐标几何，标志了从天文、地理坐标到近代坐标几何学的抽象和过渡，他的坐标思想对现代坐标的建立迈出了决定性的一步.奥雷姆的《论质量与运动的结构》(约1350)等书在1482—1515年间重印了多次，影响了文艺复兴以后包括笛卡儿在内的学者，在这个意义上，奥雷姆可以称为解析几何的先驱.在奥雷姆之后，法国数学家笛卡儿(Descartes，1596～1650)和费马(Pierre de Fermat，1601～1665)受韦达(Viète，1540～1603)等学者代数符号体系的影响，将坐标法系统运用于几何中，开启了符号体系下几何问题代数化和代数问题几何化的两个途径,实现了曲线和方程的一一对应，创立了解析几何学，笛卡儿和费马也被称为解析几何的创始人.

虽然“坐标”的雏形在古埃及时期就已有之，但是，“坐标”(coordinata) 这一名词，直到1692年才由德国数学家莱布尼兹(Leibniz，1646～1716)首先创用(9)Ruth M Tapper.coordinates in the histrory of mathematics[J]. Peoria:school science and mathematics,1929(7)：738.“纵坐标”在1694年为菜布尼兹所正式使用，而“横坐标”到18世纪才由法国数学家沃尔夫(Christian von Wolf, 1679～1754)等人引入(10)梁宗巨.世界数学通史简编 [M].沈阳：辽宁人民出版社，1980:201.

2 古希腊椭圆方程的肇始

圆锥曲线的研究，始于古希腊三大几何问题中的倍立方问题(11)白尚恕. 圆锥曲线小史[J].数学通报，1964(4)：36-41，希腊时期著名数学家均有所涉猎和建树，并影响到近代解析几何的创立.

2.1 椭圆的原始定义

公元前4世纪，古希腊学者蒙爱启马斯(Meneachinus，约公元前 375～325 )发明了圆锥曲线(12)F.Cajori.初等算学史[M].曹丹文,译.上海：商务印书馆，1925：55，他是系统研究圆锥曲线的第一人(13)梁宗巨.世界数学史简编 [M].沈阳：辽宁人民出版社，1980:109.据盖米诺斯(Geminus,约公元前70)记载，古希腊数学家是用旋转直角三角形(围绕着一条直角边)来产生圆锥面，不动的直角边叫做轴，斜边叫做母线(14)Apollonious.圆锥曲线(V-VII)[M].朱恩宽,等,译. 西安：陕西科学技术出版社，2011：3.这样旋转而成的圆锥就是直圆锥.蒙爱启马斯用垂直于直圆锥一条母线的平面，分别去截顶角为直角、锐角和钝角的直圆锥,得到了三种不同的圆锥截线.其中截锐角圆锥所得的截线称为“锐角圆锥截线”，这种截线就是现在的“椭圆”.“锐角圆锥截线”是最早对椭圆的称谓，这就是椭圆视为圆锥截线的原始定义的由来.

希波克拉底(Hippcocrates 公元前460年前后活动于雅典)把倍立方问题归结为在线段a和2a之间插入两个等比中项x,y的问题(15)梁宗巨.世界数学史简编 [M].沈阳：辽宁人民出版社，1980:109-110.用现代符号语言表述，即是蒙爱启马斯认识到，a:x=x:y=y:2a与x2=ay或y2=2ax以及xy=2a2相当，由此导致圆锥曲线的探讨.但是，由上述比例式无法导出椭圆.希腊天文学家、数学家和地理学家埃拉托色尼(Eratosthenes，约公元前276～195)认为，蒙爱启马斯的三类曲线，实际上只有两类圆锥曲线，即抛物线(x2=ay或y2=2ax)和等轴双曲线(xy=2a2).

尽管蒙爱启马斯没有用到椭圆，但在圆锥曲线中，椭圆应该是最早被发现的(16)汪晓勤,韩祥临.中学数学中的数学史[M].北京：科学出版社，2002: 172.希腊人很早就知道，圆柱或圆锥被平行于底面的平面截得的截线是圆.平面不平行于底面时的截线自然也就引起希腊人的注意.希思(T.Heath,1860～1941)认为：蒙爱启马斯完全可以用同样的方法获得椭圆的性质(17)Heath T.A History of Greek Mathematics(II)[M]. London:Oxford university press，1921：110.对椭圆的起源，卡茨(Victor J.Katz)还有一种推测，圆锥曲线看上去就像太阳做周日圆周运动时晷影的运动路径，这路径本身是落在以日晷的头端为顶点的对顶圆锥的底面上(18)Victor J.Katz.数学史通论[M].李文林,等,译.北京：高等教育出版社,1980：92.这里是周日运动是指太阳的视运动.古人不知道地球自转一周形成昼夜，而把昼夜循环看作是太阳的圆周运动.按这种想法，投影所成的平面就是截平面.进一步会注意到,从平面外一点看圆的形状就像是一椭圆.

2.2 椭圆的第二定义

与欧几里得同时代的亚里斯塔欧(Aritaeus,约公元前370～275)，著有《立体轨迹》5卷，已失传.根据帕普斯(Pappus，约290～350)记载，这是一部关于圆锥曲线的论著.之所以使用“立体轨迹”而不是“圆锥曲线”，原因是当时把“圆锥曲线”视为“轨迹”，而命名为“立体”轨迹，在于该轨迹是从立体图形产生的(19)Heath T.A History of Greek Mathematics(II)[M]. London:Oxford university press,1921：116—118.

希腊数学黄金时代的三大代表人物欧几里得( Euclid,约公元前330～275)、阿基米得和阿波罗尼奥斯，都在总结前人成果的基础上，推进了圆锥曲线的研究.欧几里得的著作除广为流传的《几何原本》之外，还有《圆锥曲线论》4卷，《面轨迹》2卷，只是后两部均已失传.据希思研究，欧几里得曾在《面轨迹》中不加证明地给出圆锥曲线如下的重要命题：到定点与到定直线的距离之比的点的轨迹是圆锥曲线(20)汪晓勤,韩祥临.中学数学中的数学史[M].北京：科学出版社,2002:174.用现代语言来解释，当这个“比”介于0到1之间时，形成的轨迹就是椭圆.它就是今天利用焦点-准线性质刻画的椭圆第二定义.该定点在阿波罗尼奥斯《圆锥曲线论》中，称为“由贴合产生的点”，“焦点”这一术语，最早是德国天文学家开普勒(Johannes Kepler，1571～1630)在1604年创用(21)Victor J.Katz.数学史通论[M].李文林,等,译.北京：高等教育出版社,1980：93，而“准线”一词，则是之后由荷兰数学家让·德·维特(J.D.Witt ，1623～1672)创用的(22)汪晓勤.椭圆第一定义是如何诞生的[J].中学数学月刊,2017(6)：30.这一命题由希腊后期数学家帕普斯得以证明.相比而言，亚里士塔欧对圆锥曲线的工作更专业和更具原创性，而欧几里得主要是对圆锥曲线的汇编和对内容的重新排列(23)Heath T.A History of Greek Mathematics(II)[M]. London:Oxford university press,1921：116—117.

阿基米德早年曾在亚历山大跟随欧几里得的门徒学习，他曾引用欧几里得《面轨迹》中的一些零散的命题(24)杜石然.孔国平.世界数学史[M].长春：吉林教育出版社,2009:72，并且阿基米德有关圆锥截线的研究也保留了下来.欧几里得和阿基米德仍然沿用蒙爱启马斯对圆锥曲线的名称(如“椭圆”称为“锐角圆锥截线”)，阿基米德给出了圆锥曲线中椭圆的直径这个名称(即现在椭圆的长轴)(25)Heath T.A History of Greek Mathematics(II)[M]. London:Oxford university press,1921：122，证明了如下的椭圆性质：

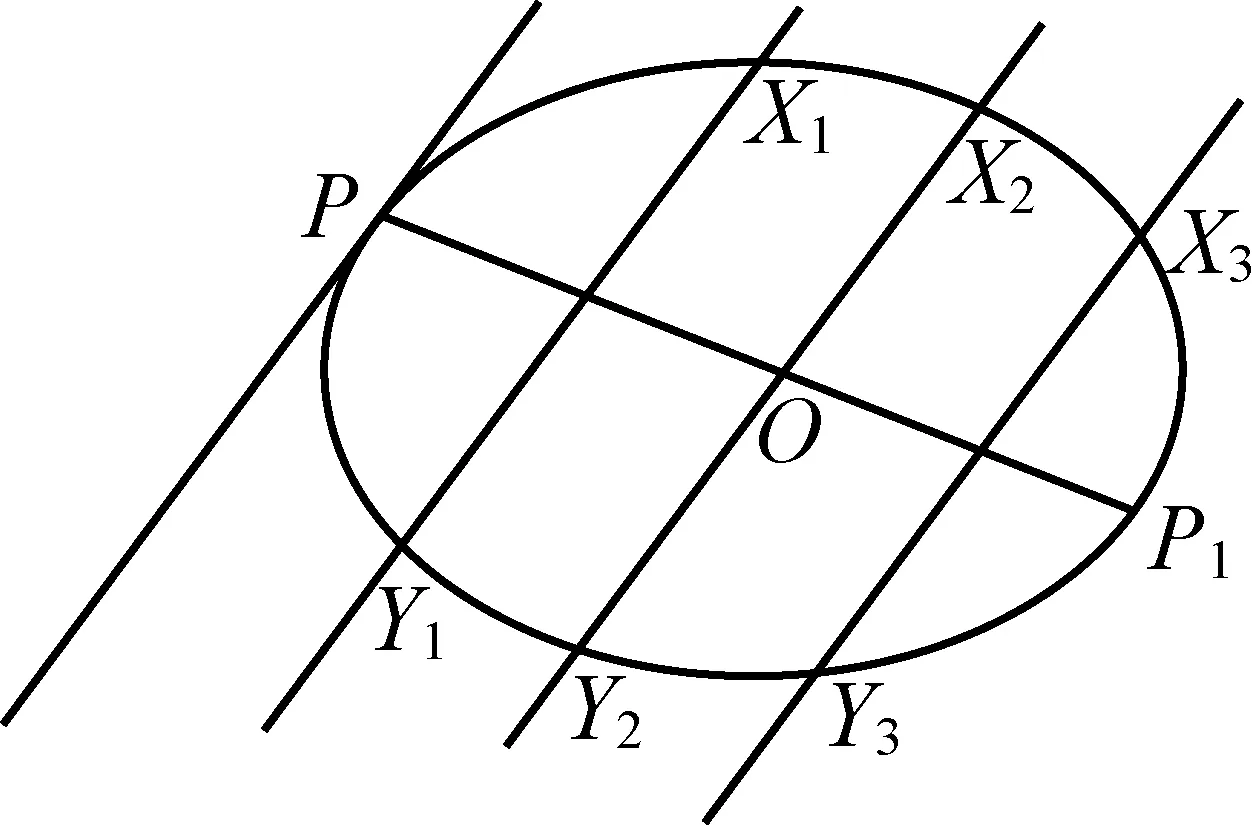
图1

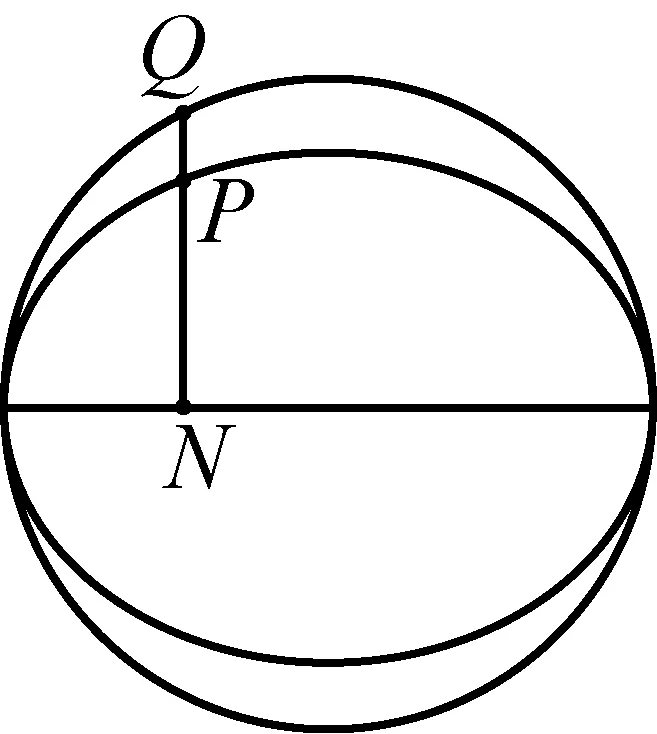
图2

椭圆中心O与切点P的连线平分所有平行于切线的弦(如图1)，设P是椭圆上一点，PN垂直于直径，N为垂足，延长NP交辅助圆于Q,则QN∶PN为常数(如图2)等.由此可以看出，阿基米德已经有了用直径或与之相交的切线表述椭圆性质的意识.

另外，阿基米德在他的《劈锥曲面体与旋转椭圆体》中表明,任一椭圆都可看作圆锥的截线，该圆锥不一定是直圆锥，其顶点的选择有很大的任意性(26)Archimedes.Heath T(编).阿基米德全集[M].朱恩宽,等,译.西安：陕西科学技术出版社,2011：5.因此，阿基米德可能把直圆锥扩充到了斜圆锥，从而获得圆锥曲线的一些性质，但未给出证明(27)Heath T.A History of Greek Mathematics(II)[M]. London:Oxford university press,1921：122-123.

2.3 对顶锥的创用与坐标制思想的萌芽

阿波罗尼奥斯是古希腊圆锥曲线研究集大成者.他编写的《圆锥曲线论》共有8卷，只有前7卷保存下来.根据帕普斯记载，阿波罗尼奥斯编写的《圆锥曲线论》前4卷是以欧几里得的《圆锥曲线论》4卷为基础的(28)Heath T.A History of Greek Mathematics(II)[M]. London:Oxford university press,1921：119.这可能与阿波罗尼奥斯很小的时候就去亚历山大和欧几里得的继任者一起学习有关.

阿波罗尼奥斯采用平面截斜圆锥得到了椭圆，用几何方法给出椭圆的基本性质，用现代符号描述：

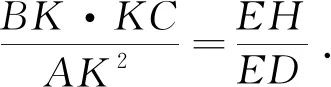
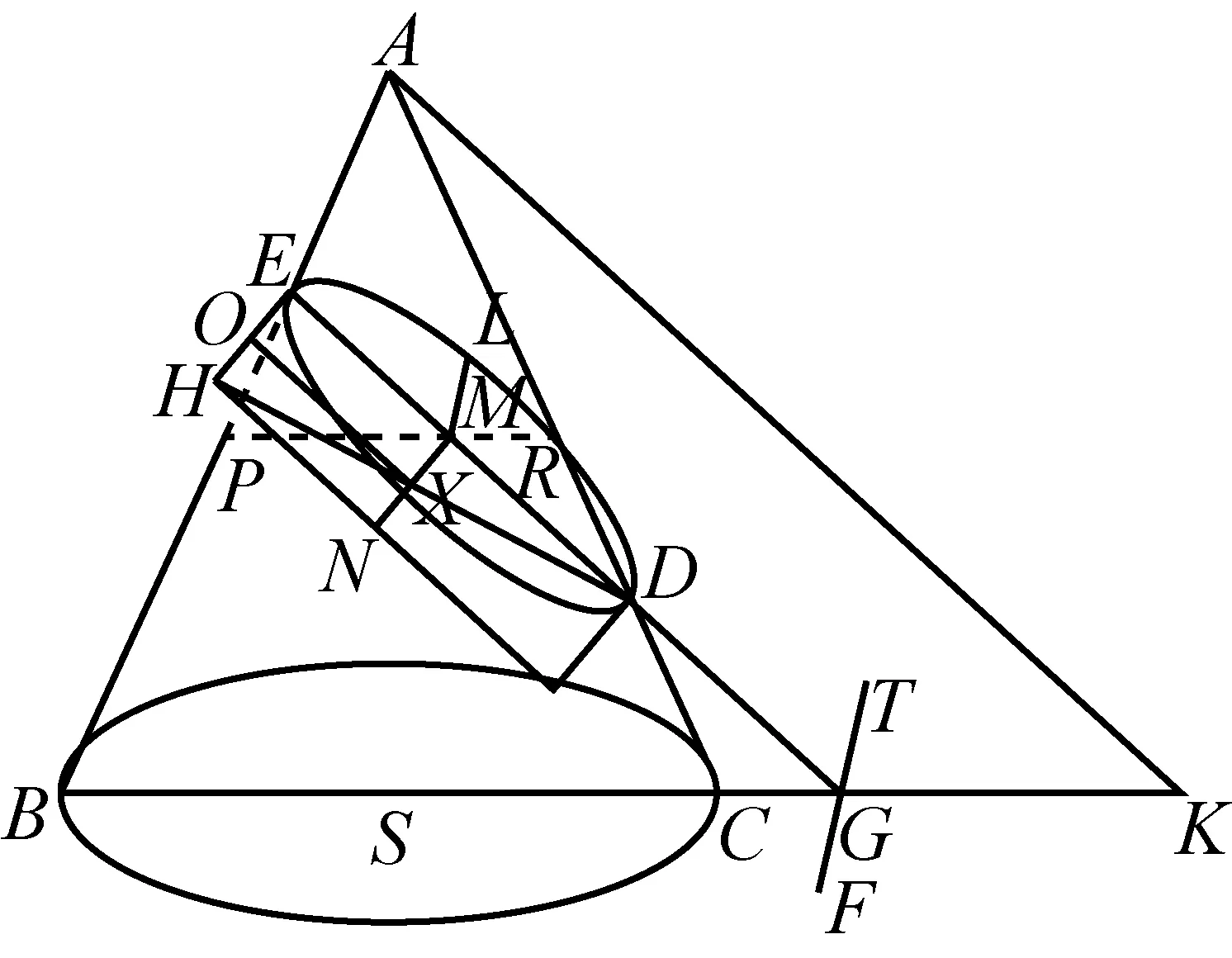
图3

阿波罗尼奥斯把直径(ED)上的线段(EM)叫做横线，对应的半弦(ML)叫做纵线，线段(EH)叫做截线的竖直边，对应参量p是一个常数，就是椭圆通径.

对以一个顶点为原点，长轴为横轴的椭圆性质描述如下(31)Archimedes，Heath T(编).圆锥曲线论(I—IV卷)[M].朱恩宽,译.西安：陕西科学技术出版社，2018：6-8：

以横线(EM，EM在直径上)为一边做矩形(EMXO)，“贴合”到竖直边(EH)上去，使其面积等于纵线(ML,L在椭圆上)上正方形(ML2)，且矩形(EMXO)比横线(EM)和竖直边(EH)所夹的矩形(EMNH)，缺少一个与横截直径(ED)和竖直边(EH)所交的矩形相似的矩形(OXNH).在这里，纵线上正方形的矩形另一边EO小于竖直边EH.

其含义就是：椭圆其上任一点纵坐标组成的正方形小于与之对应的横坐标及通径组成的矩形.

阿波罗尼奥斯在圆锥上使用相交的横线(EM)和纵线(EL)，利用线段生成的矩形和正方形的面积刻画椭圆性质，实际上建立了只有正数的斜坐标系，已经含有坐标制的基本思想.

阿波罗尼奥斯对椭圆的轨迹进行了描述，表示为现代符号语言为：

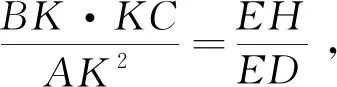
阿波罗尼奥斯还发现亚里斯塔欧、欧几里得等学者熟知但并未完整解决的三、四线轨迹问题.他完整地解决三线轨迹问题，而三、四线轨迹问题也成为了从希腊后期直到17世纪数学家如帕普斯、笛卡儿、费马等所讨论的热点.帕普斯对三、四线轨迹问题做了进一步的研究，并明确地指出了“三线轨迹”和“四线轨迹”为圆锥曲线，“五线及以上轨迹”不再是人们已经知道的圆锥曲线，而是属于“线轨迹”(32)Bos.Henk J.M. Descarts′ solution of Pappus′ problem.sources and studies in the History of Mathematics and Phyical Sciences[M].Springer-Verlag New York Inc，2001：315-317

阿波罗尼奥斯如此深奥的内容完全是用文字表达的，没有使用符号和公式，命题叙述冗长，但他建立了相对完美的圆锥曲线理论，他的工作直到17世纪笛卡儿之前一直无人能够超越.

3 近代椭圆方程的发展

解析几何的基本思想就是借助坐标系建立点与实数对的一一对应，以及曲线与方程的一一对应.解析几何的创立，为微积分的诞生搭建了舞台，近代数学因此而进入快速发展时期.

3.1 解析几何的开端

1607年，笛卡儿在《更好地指导推理和寻求科学真理的方法论》一书附录《几何》中，从四线轨迹出发，通过比例关系推出了椭圆方程(33)Smith.E.D&Martha L.The geometry of Rene′Descartes[M]. New York: Dover Publications.Inc，1954：59-63.笛卡儿受韦达等学者代数符号体系的影响，率先将代数符号引入到坐标当中，其推导椭圆方程过程如下：

如图4，设AB、AD、EF、GH是给定的四条直线，已知CB·CF=CD·CH(四线轨迹的性质)，求C的轨迹.

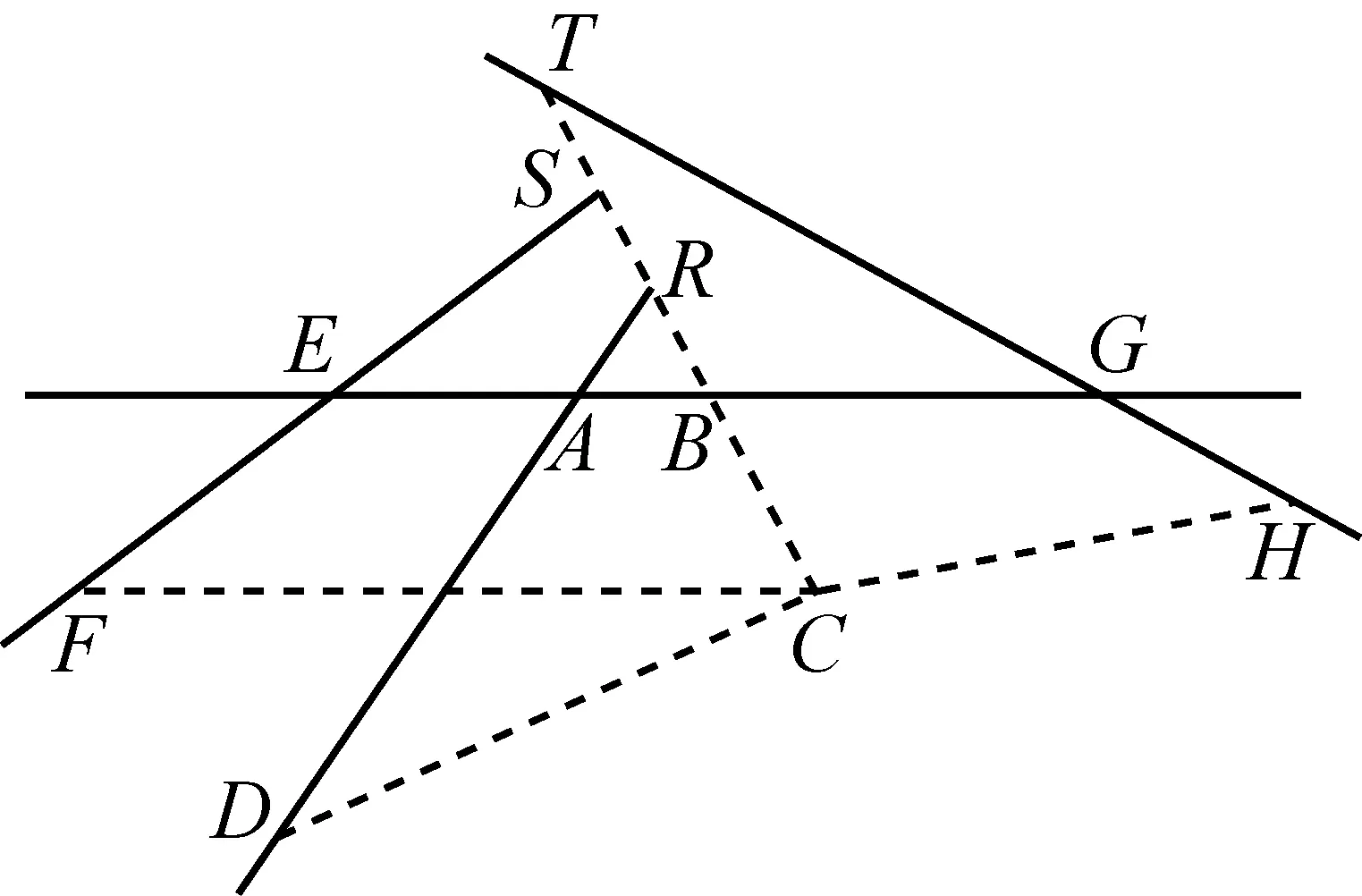
图4

笛卡儿取AB为横轴，A为原点，设AB=x，BC=y,可得如下的比例AB:BR=z:b,CR:CD=z:c，AK=k,BE:BS=z:d，CS:CF=z:e,AG=l,BG:BT=z:f，其中b,c,d,e,f,l,k,z为常数.通过比例的相关计算得：

再将上述式子代入CB·CF=CD·CH中，可推导出一个代数形式的轨迹方程：

可验证，该四线轨迹是椭圆.

同一时期，法国数学家费马在《平面与立体轨迹引论》中，从椭圆的基本性质出发，采用韦达等学者的代数符号，推导证明了表示椭圆的方程，其过程大致如下(34)Struck.D. J. A Source Book in Mathematics. 1200-1800[M].Princeton: Princeton University Press，1986：148-150:

如图5，设OA=OA′=b，ON=x,PN=y，PN垂直OA(注：PN和OA可垂直也可不垂直，而费马一般采用的是垂直)，则A′N=b+xAN=b-x.

图5

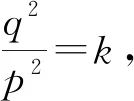
笛卡儿在推导椭圆方程过程中，采用的是斜坐标系思想.坐标系只有一条坐标轴(横轴)，用于度量第二个未知量Y的线段,并没有明确说明是纵轴，它与横轴也不一定垂直，但在双曲线推导过程中，笛卡儿采用的是直角坐标系(35)Ruth M Tapper.coordinates in the histrory of mathematics[J]. Peoria:school science and mathematics，1929(7)：742—743.而费马在推导椭圆方程过程中，更多地采用直角坐标系.笛卡儿和费马对于坐标的认识还局限为正数.

符号化是迈向现代数学的关键一步.笛卡儿和费马在坐标描述中引进现代符号，建立斜坐标系或直角坐标系，利用一对线段长x和y确定点的位置，求得椭圆的轨迹方程.在正数情况下，一对线段长和一对实数对是可以相互确定的，所以，一对线段长x和y确定点的位置就相当于用实数对(X,Y)确定点的位置.另外，笛卡儿用坐标概念把方程看为平面曲线，再以曲线图解代数方程；费马用韦达的符号研究二次方程，既把圆锥曲线看为圆锥的平截线，也看为平面轨迹，同时又看为二次方程的图象.这已经含有用实数对确定点的位置，曲线与方程对应的解析几何的基本思想.由此，笛卡儿和费马也因此被称为解析几何的创始人.

3.2 椭圆方程的第一定义

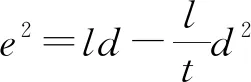
荷兰数学家让·德·威特在其《曲线基础》(1646,该书被誉为历史上第一部解析几何教材)中给出了两类椭圆方程的标准形式(37)Boyer. C. B. History of Analytic Geometry[M]. New York:Scripta Mathematica，1956：114-117:

但未发现方程中常数f、l/g代表的几何意义,并总结出任何有两个变量的二次方程都可以化为标准形式的其中一个.

让·德·威特还证明了命题:平面上到两定点距离之和等于常数的动点轨迹为椭圆，即椭圆的第一定义.以此为基础，后来的数学家用不同的方法推导出了椭圆的方程.

3.3 椭圆标准方程的形成

法国数学家居西尼(Guisnee，16？～1718)第一次使用了直角坐标系，在《代数在几何中的应用》(1705)中，以椭圆的中心和左顶点为坐标原点，均建立了直角坐标系，用a,b来表示有心曲线的长、短半轴，在圆锥上利用几何法推导出了椭圆的方程(38)Guisnee. N. Application de I′Algebre à la Geometrie[M]. J. Bourdot et J. Quillau, 1705： 71-72.

法国数学家洛必达(L.Hospital,1661～1704)在《圆锥曲线分析》(去世后整理出版，1720)(39)L'Hospital. M.de. Traité Analytique des Sections Coniques[M].Paris: Montalant,1720：22-25中，利用椭圆的第一定义，引入参数，利用两点间的距离公式，推导出了椭圆的方程，在推导过程中还引入了焦半径.同时，他把椭圆方程的推导放在了平面上，以椭圆中心为原点建立直角坐标系，将两种椭圆方程的形式进行了转化(长轴和短轴为已知条件的椭圆方程、长轴和通径为已知条件的椭圆方程).

英国数学家斯蒂尔(R.Steel)在其《圆锥曲线论》(1745)中，在平面上仍然采用椭圆的第一定义，采用余弦定理方法推导出了椭圆方程(40)Steell. R. A Treatise of Conic Sections[M]. London: St John's Gate, 1745：16-18.

在居西尼、洛必达和斯蒂尔的关于椭圆方程的推导中，和笛卡儿和费马一样，均采用x，y对应线段，只使用单一坐标轴(横轴X轴)，也没有使用纵横负坐标.沃利斯是有意识地引进负向横坐标的第一人(41)Boyer.C. B. History of Analytic Geometry[M]. New York:Scripta Mathematica,1956：110-114.而英国数学家牛顿(Newton，1642～1727)在他的《自然哲学的数学原理》(光学篇)(1687)中，进一步运用了纵向负坐标(42)白尚恕.圆锥曲线小史[J].数学通报,1964(4)：36-41.虽然欧拉(Leonhard Euler ，1707～1783)等人偶然也用过Y轴，但是瑞士数学家克拉美(Gabriel Cramer,1704-1752)在《代数曲线分析引论》(1750)中才正式引入纵轴Y轴(43)梁宗巨.世界数学史简编 [M].沈阳：辽宁人民出版社,1980:201.

英国数学家赖特(J.M.F.Wright)在《圆锥曲线与其他曲线的代数体系》(1836)中，在平面内采用椭圆的第一定义，他运用直角坐标系，用实数对表示坐标位置，标准地使用了横纵向的正负坐标，利用“平方差法”推导出了现在的椭圆标准方程形式(44)Wright.J. M. F. An Algebraic System of Conic Sections &other curves[M]. London: Black & Amstrong, 1836：94-99.

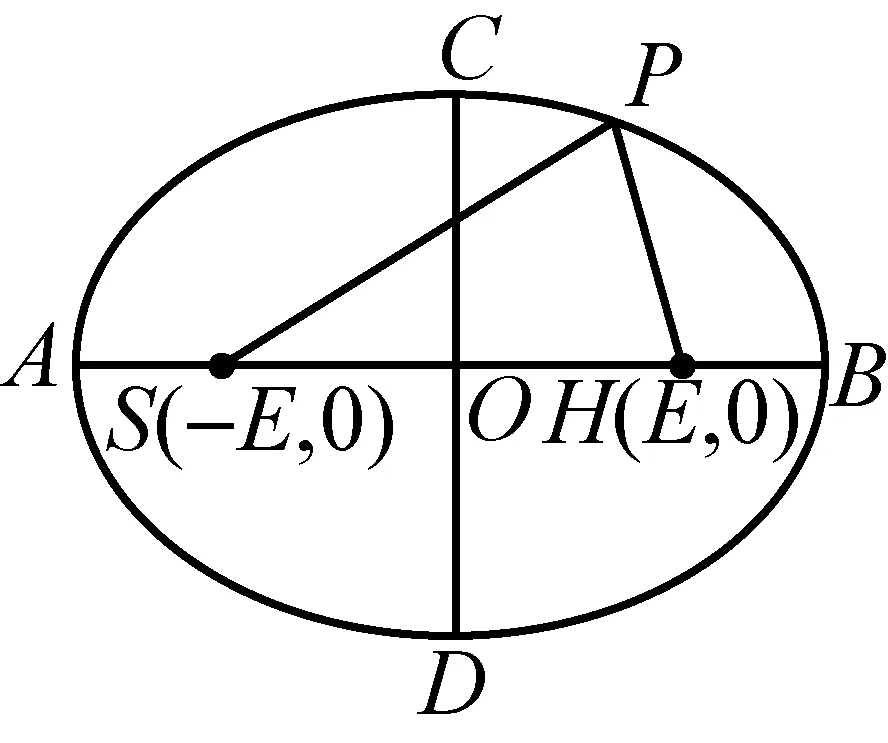
图6

如图6，设椭圆的中心为O，左右、上下顶点分别A,B,C,D，左右焦点为S,H,|AB|=2a，焦距|SH|=2E.由SP+PH=2a，

又SP2=SM2+PM2=(E+x)2+y2， ①

HP2=HM2+PM2=(E-x)2+y2，②

①-②得SP2-HP2=4Ex

=(SP+PH)(SP-PH)=2a(2SP-2a)，

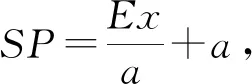
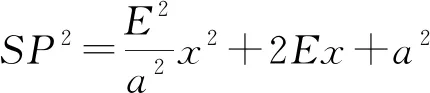
=E2-2Ex+x2+y2，

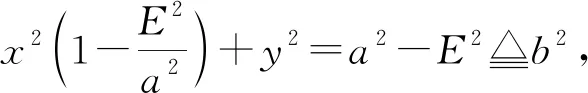
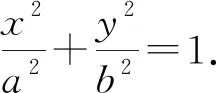
至此，坐标体系已经基本完成，能够标准地建立直角坐标系，并用实数对表示坐标位置，标准地使用横向和纵向的正负坐标，推导圆锥曲线的方程和性质.在此基础上，椭圆方程也完成了文字叙述到符号表达的现代标准形式的演变过程.

18世纪，瑞士数学家欧拉建立了完备的圆锥曲线理论.他在《分析引论》(1748)中，系统地建立了直角坐标、斜坐标及极坐标的概念，给出了坐标的变换公式和转轴公式.19世纪中叶，各种坐标制的建立，又把圆锥曲线的理论推进了一步.19世纪末，受分析学的影响，圆锥曲线在理论发展上达到高峰，在实际应用中也得到了充分利用.

圆锥曲线学在明末第一次输入中国，与当时的历法书籍有关(45)白尚恕.圆锥曲线小史[J].数学通报,1964(4)：36-41.清中叶第二次输入，比较有影响的是李善兰和伟烈亚力合译的《代微积拾级》(1859)，书名中的“代”，指的就是“解析几何”.谢洪赉，潘慎文翻译的《代形合参》(1893)，是中国第一本全面、系统介绍西方解析几何学的教科书，其内容包括平面与立体解析几何.清末废科举兴学堂后，解析几何成为新学的必修科目(46)钦定学堂章程.1902(47)奏定等学堂章程.1904.解析几何首先进入大学课堂，如1907年两江师范学堂就开设了解析几何课程(48)苏云峰.三(两)江师范学堂——南京大学的前身(1903-1911)[M].南京：南京大学出版社,2002：45，1922年才开始全面进入中学数学教科书.之后，圆锥曲线得到了广泛地流传.民国时期商务印书馆、中华书局等出版了更多的自编或翻译的解析几何教科书.直至如今，以圆锥曲线为主要内容的解析几何，仍然是高中数学的必修科目，其方程和坐标的历史，体现了解析几何的基本思想，具有丰富的教育价值.