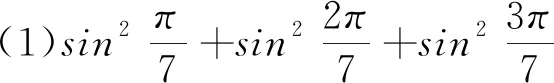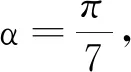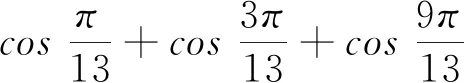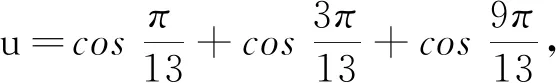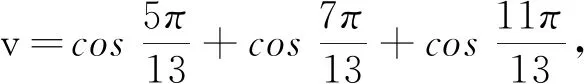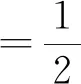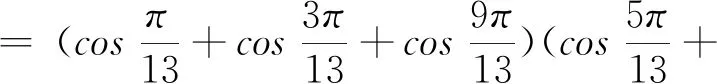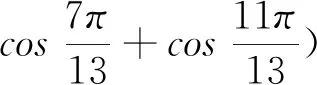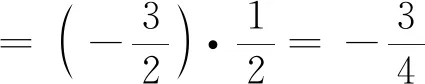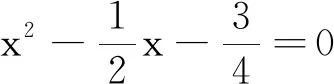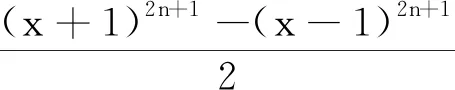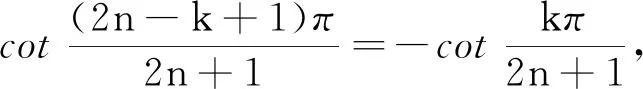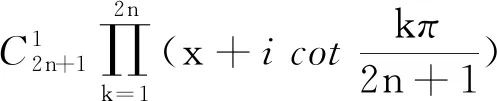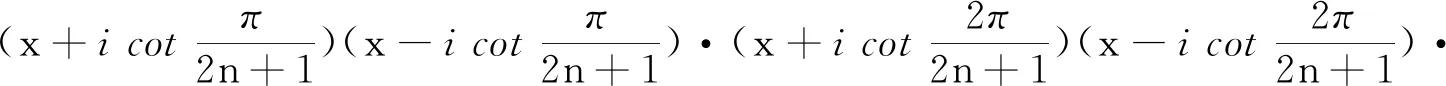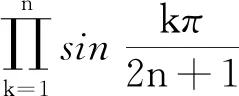应用方程方法解答非方程问题
杨学枝
(福建省福州第二十四中学 350015)
方程是中学数学教学中一块极为重要的内容,在数学教学中,一定要重视对方程的教学,深刻理解方程定义、方程性质,并善于应用方程的方法去解答非方程的数学问题,这样常常可以得到简捷解题效果.由此,本文将举数例说明方程在证明等式、不等式等方面的应用,同时可以看出,应用方程的方法解题的优越性.
1 应用方程证明恒等式
例1设ai,bi(i=1,2,…,n)是两组复数,ai(i=1,2,…,n)互不相等,满足
(a1+b1)(a1+b2)…(a1+bn)
=(a2+b1)(a2+b2)…(a2+bn)=…
=(an+b1)(an+b2)…(an+bn).
求证:
(1)(a1+b1)(a2+b1)…(an+b1)
=(a1+b2)(a2+b2)…(an+b2)=…
=(a1+bn)(a2+bn)…(an+bn);
(2)a1+a2+…+an+b1+b2+…+bn=0.
证明(a1+b1)(a1+b2)…(a1+bn)
=(a2+b1)(a2+b2)…(a2+bn)=…
=(an+b1)(an+b2)…(an+bn)=m,
则x=a1,a2,…,an可看作方程(x+b1)(x+bn)…(x+bn)-m=0的n个不同的根,因此,根据方程的基本定理可知,对于任意复数x有以下恒等式
(x+b1)(x+b2)…(x+bn)-m
=(x-a1)(x-a2)…(x-an).
①
(1)在式①中,分别令x=-b1,-b2,…,-bn,即得
(a1+b1)(a2+b1)…(an+b1)
=(a1+b2)(a2+b2)…(an+b2)=…
=(a1+bn)(a2+bn)…(an+bn)
=(-1)n+1m.
(1)中的等式获证.
(2)将式①展开后,根据多项式性质,比较两边系数,即得(2)中的等式.
同理,类似(2)的解法,由式①还可得到其他有关等式,如:
等等.
在本例中,要善于从等式形式看到方程的本质,从而应用方程基本定理求解,这种解法要较其他方法清晰、简捷.
欧拉(L. Euler, 1707-1783, 瑞士)是十八世纪最著名的数学家,他不仅在高等数学的各个分支中,取得了广泛成就,就是在初等数学中,也到处留下了欧拉的足迹.其中有一个鲜为人知的关于分式的欧拉公式:
上述分式的欧拉公式可以进一步加以推广,得到一个更为一般的如下分式等式:
例2设xk(k=1,2,…,n,n≥2)是n个互不相等的复数,则有
(1)
(2)
(3)
证明由于证法类似,下面我们仅就2≤m=n时的情况用数学归纳法给予证明,以下字母均符合定理1所给的条件.
当n=2时,不难证明
=(x1+x2)-(t1+t2),
事实上,我们如果记
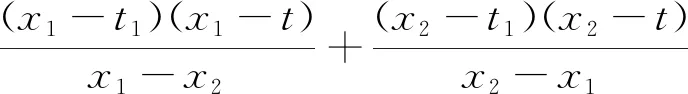
-(x1+x2)+(t1+t),
可视为以t为字母的小于或等于一次多项式,由于f(x1)=f(x2)=0,又x1≠x2,因此f(t)=0,再取t=t2,便证明了n=2时式(3)成立.
假设n=k时,式(3)成立,即
今记f(t)等于
可视为其关于t的小于或等于一次多项式,命t=x1和t=x2,根据假设可知f(x1)=f(x2)=0,又由于x1≠x2,因此有f(t)=0,取t=tk+1得到f(tk+1)=0,即
这说明当n=k+1时,式(3)也成立.由以上可知,对于n≥2的任意自然数时,式(3)总成立,证毕.
本例解答中巧妙地应用了多项式性质.
例3设n个数xi∈C,i=1,2,…,n,其初等对称多项式为si(i=1,2,…,n)又x1,x2,…,xn两两互不相等,则
…………
证明由题意可知,xi∈C,i=1,2,…,n是方程xn-s1xn-1+s2xn-2-…+(-1)nsn=0的n个根,由此反过来,我们可以将以下方程组看成是关于未知数是s1,-s2,…(-1)n-1sn的方程组:
本例解答中巧妙地将一元n次方程问题转化为n元一次方程组问题求解,将一元n次方程的各项系数看成n元一次方程组n个未知数,将xi(i=1,2,…,n)作为已知数,解出n元一次线性方程组.

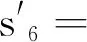
…,
证明由已知条件可知,a1,a2,…,an是方程
xn-s1xn-1+s2xn-2-s3xn-3+…+(-1)nsn
=0
的n个根.
当n为奇数时,将上述方程变换后两边平方,得到
x2(xn-1+s2xn-3+…+sn-3x2+sn-1)2
=(s1xn-1+s3xn-3+…+sn-2x2+sn)2,
在上式中令y=x2,得到方程
展开整理即为
当n为偶数时,将上述方程变换后两边平方,得到
(xn+s2xn-2+…+sn-2x2+sn)2
=x2(s1xn-2+s3xn-4+…+sn-3x2+sn-1)2,
在上式中令y=x2,得到方程
展开整理即为
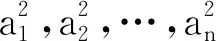
的n个根,于是,根据方程根与系数关系,即得原命题中的诸个等式.
本例是应用方程根与系数关系的典型例子,根据方程根与系数关系构造一元n次方程,并对这个方程进行平方变换,然后再次利用方程根与系数关系一举获得一揽子等式.
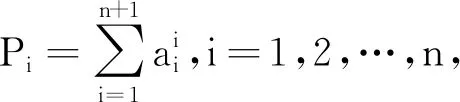
证明由题意xi(i=1,2,…,n,n+1)是方程
xn+1-s1xn+s2xn-1-…+(-1)nsnx+(-1)n+1sn+1=0
的n+1个根,若这n+1个根均不为零时,则上述方程可以写成
=0,
于是,有
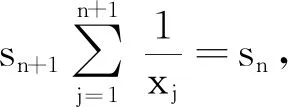
Pn-s1Pn-1+s2Pn-2-s3Pn-3+…+(-1)n-1sn-1P1+(-1)n(n+1)sn+
(-1)n+1sn=0,
即得
Pn-s1Pn-1+s2Pn-2-s3Pn-3+…+(-1)n-1sn-1P1+(-1)nnsn=0.
若xi∈C(i=1,2,…,n+1),其中有一个根为零,不妨设xn+1=0,其余n个均不为零,这时,问题变为:
设xi∈C,i=1,2,…,n,其初等对称多项式为si(i=1,2,…,n),则
Pn-s1Pn-1+s2Pn-2-s3Pn-3+…+(-1)n-1sn-1P1+(-1)nnsn=0,
由题意xi(i=1,2,…,n,)是方程
xn-s1xn-1+s2xn-2-…+(-1)n-1sn=0
的n个根,由于这n个根均不为零,则上述方程可以写成
于是,有
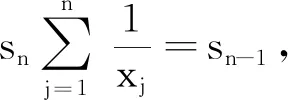
Pn-s1Pn-1+s2Pn-2-s3Pn-3+…+(-1)n-1nsn-11+(-1)nsn-1=0,
即得
Pn-s1Pn-1+s2Pn-2-s3Pn-3+…1+
(-1)n-1(n-1)sn-1=0,
原式也成立.故原式获证.
更一般的有牛顿等幂和公式,读者可参见文献[3]
例6设ABCD是平面凸四边形四边长为AB=a,BC=b,CD=c,DA=d,对角线长为AC=m,BD=n,有一对对角和为900,则
i)(a2b2+c2d2)m2+(a2d2+b2c2)n2
=2(b2c2d2+a2c2d2+a2b2d2+a2b2c2);
ii)m2n2=a2c2+b2d2.
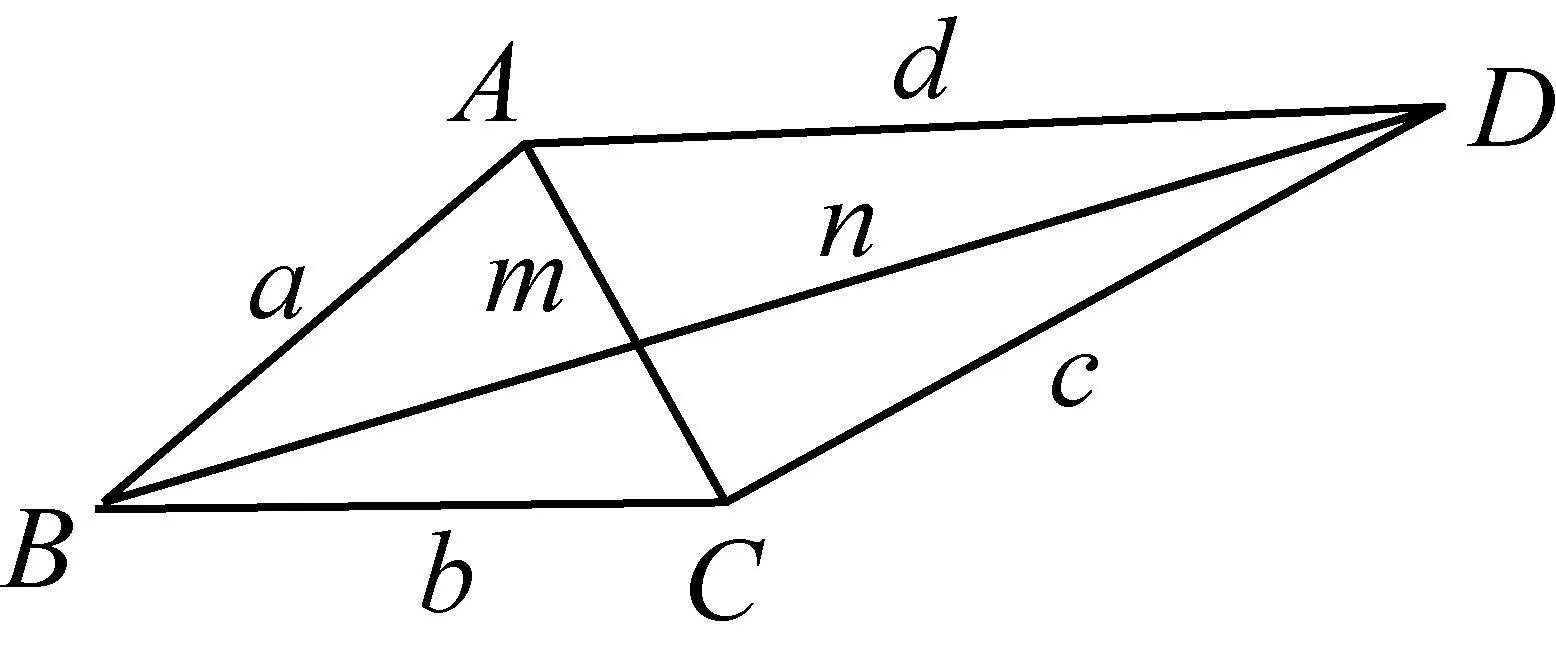
证明由已知条件,得到
cos2∠ABC+cos2∠CDA=1,
利用余弦定理,有
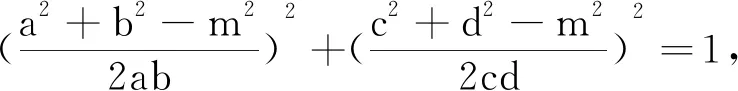
经整理得到
(a2b2+c2d2)m4-2(b2c2d2+a2c2d2
+a2b2d2+a2b2c2)m2
+(a2c2+b2d2)(a2d2+b2c2)=0,
上式两边同乘以(a2b2+c2d2),得到
(a2b2+c2d2)2m4-2(a2b2+c2d2)(b2c2d2+a2c2d2+a2b2d2+a2b2c2)m2
+(a2b2+c2d2)(a2c2+b2d2)(a2d2+b2c2)
=0.
①
同理由cos2∠BCD+cos2∠DAB=1,可得到
(a2d2+b2c2)2n4-2(a2d2+b2c2)(b2c2d2+a2c2d2+a2b2d2+a2b2c2)n2
+(a2b2+c2d2)(a2c2+b2d2)(a2d2+b2c2)
=0.
②
由以上①、②两式可知,(a2b2+c2d2)m2和(a2d2+b2c2)n2是以下方程
x2-2(b2c2d2+a2c2d2+a2b2d2+a2b2c2)x
+(a2b2+c2d2)(a2c2+b2d2)(a2d2+b2c2)=0,
的两个根,于是由方程根与系数关系便得到
(a2b2+c2d2)m2+(a2d2+b2c2)n2
=2(b2c2d2+a2c2d2+a2b2d2+a2b2c2);
(a2b2+c2d2)m2·(a2d2+b2c2)n2
=(a2b2+c2d2)(a2c2+b2d2)(a2d2+b2c2),
即
m2n2=a2c2+b2d2.
故原命题获证.
本例应用方程根与系数关系使得解答一举两得,而且计算简便.
注:本例还有多种解法,但应用方程的方法求解较为简捷.


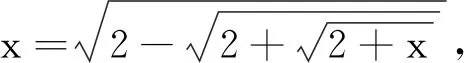
展开并整理得到以下八次方程
x8-8x6+20x4-16x2-x+2=0,
即
(x+1)(x-2)(x3-3x+1)(x3+x2-2x-1)
=0.
①
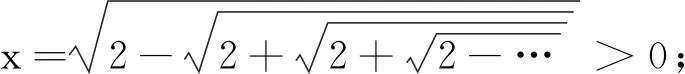

用反证法.

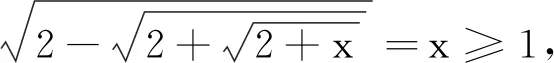
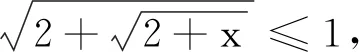
上式左边大于1,故不成立,
因此有 0 于是(x+1)(x-2)≠0. 另外,又由于0 x3+x2-2x-1=x(x-1)(x+2)-1 <0-1=-1<0, 因此,从式①可知,只有 x3-3x+1=0. 由于x3-3x+1 本例将求值问题转化为求方程的解的问题,这类问题我们经常会遇到. 例8设ai∈R,i=1,2,…,n,其初等对称多项式为s1,s2,…,sn,若si>0,i=1,2,…,n,则ai>0,i=1,2,…,n. 证明由题意可知a1,a2,…,an是方程 xn-s1xn-1+s2xn-2-s3xn-3+…+(-1)n-1sn-1x+(-1)nsn=0 的n个非零根. 当n为偶数时,由原方程式得到 注意到上式分子、分母中各项均大于零,由此得到x≥0,因此ai>0.i=1,2,…,n. 当n为奇数时,由原方程式得到 注意到上式分子、分母中各项均大于零,由此得到x≥0,因此ai>0.i=1,2,…,n. 故原命题获证. 注:当n=3时,便是1965年全国高考理科数学附加试题: (1965年高考理科附加题)已知a,b,c为实数,证明a、b、c都为正数的充要条件是a+b+c>0,ab+bc+ca>0,abc>0. 本例通过改变方程写法,再根据方程定义,从而巧妙地使问题得到了简捷的解决. 本例有多种证明方法,下面应用三次方程实根判定定理,给出一个简捷的证明. ① ≤0, 将上式展开并整理即得 即 这里顺便指出,本例中的不等式应用十分广泛,特别对于一些高难度的三元不等式,常用它来证明.如下例,若用其他方法证明似乎难度较大: (自创题,2007.09.18)设a,b,c∈R+,且a+b+c=1,则 例10(自创题,2013.05.01)设x,y,z,w∈R+,且xyzw=1,记s1=x+y+z+w,s2=xy+xz+xw+yz+yw+zw,s3=yzw+xzw+xyw+xyz.则 (s1+s3)2≥16(s2-2), 当且仅当x=y=z=w=1时取等号. 证明由于x,y,z,w∈R+,且xyzw=1,则x,y,z,w中必有一个不大于1,同时必有一个不小于1,不妨设x≤1,y≥1.又由s1=x+y+z+w,s2=xy+xz+xw+yz+yw+zws3=yzw+xzw+xyw+xyz,xyzw=1,可知x,y,z,w是方程 t4-s1t3+s2t2-s3t+1=0 的四个正实数根,由此得到 ① 原命题获证. 注:可以证明有更强式:s1s3≥4(s2-2). 解由已知条件,可得 因此,x1,x2,x3,x4是方程y4-2y3-y2+2y+x1x2x3x4=0的四个根,又由于 y4-2y3-y2+2y+x1x2x3x4 =(y2-y-1)2+x1x2x3x4-1, 因此,有 x1x2x3x4=-(y2-y-1)2+1≤1, 另外,由于x1,x2,x3,x4是方程y4-2y3-y2+2y+x1x2x3x4=0的四个根,于是得到 +4x1x2x3x4 以上两例应用方程定义,方程根与系数关系,并对方程进行适当变换后应用有关不等式予以证明或求最值. 这时一道常见题,可以用三角函数有关公式求解,这里,我们用方程的方法求解,一箭双雕. 即有 在三角求值中,当n为奇数时,sinnα=0可以展开为关于sinα的n次方程式,再应用一元n次方程根与系数关系求值.这里α是一个与n有关的特定的角, 否则所写的等式一般不成立; 另外任意角的倍角的三角函数都可用单角三角函数来表出. 本例先分别求出两式的和与积,从而应用方程方法分别求出两式的值. 例14k,n∈N*,且kn≠0,则 而方程 (x+1)2n+1-(x-1)2n+1=0的2n个根为 于是,有 因此得到 若取x=1,便得到 如果将本例中等式的左边展开,再与其右边比较系数,便可得到一系列等式: 类似方法可以得到以下: 例15(自创题,1970.07.01)当n为不小于3的奇数时,求证 证明略. 如以上例14、例15及其类似问题,主要应用了方程的基本定理和复数有关公式,这是求解这类问题的常用的方法. 有许多数学问题,看似与方程无关,但经过某些变换,或考虑到与方程相关的知识,特别要注意初等对称多项式与一元n次方程的关系等,可以发现它们常常可以转化为方程问题求解,本文仅举数例说明方程在证明等式、不等式等方面的应用,只不过起到启示的作用,实际上,方程思想与方程方法是数学解题中的一个重要的解题策略,值得重视.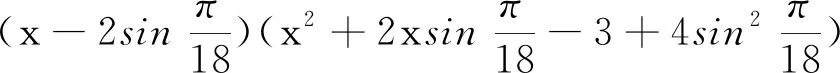
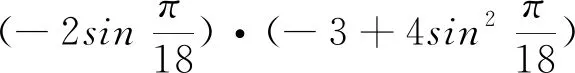

2 应用方程证明不等式或求解极值问题

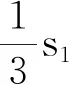
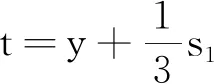
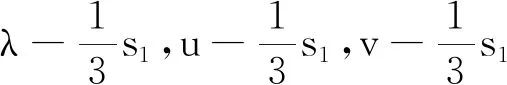
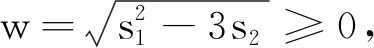
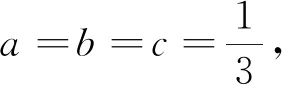

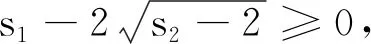
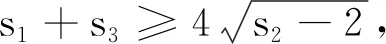
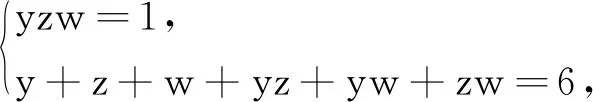
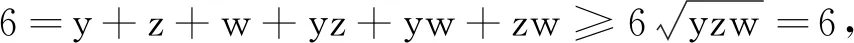
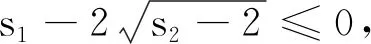
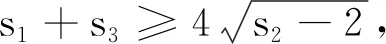
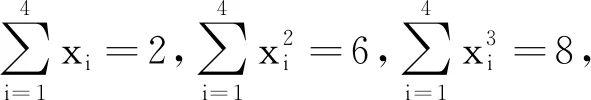
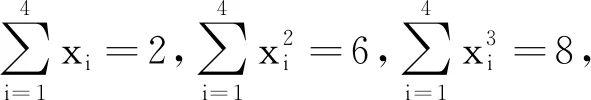
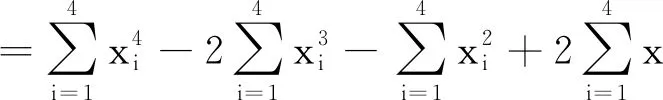
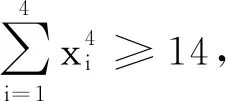
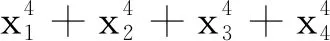
3 应用方程求三角函数式的值或证明三角函数等式