一种新型压缩空气储能装置的优化控制
樊胜军,齐向东
(太原科技大学 电子信息工程学院,太原 030024)
压缩空气储能的概念自1949年被提出以来,一直作为储能技术的研究前沿。其储能效率和经济效益仅次于抽水蓄能,但却有着不受季节因素的约束,德国、美国、日本先后将压缩空气储能电站投入商用。1978年德国率先将压缩空气储能电站的概念转化为可以商业运行的290 MW的储电站。美国紧随其后在1991年投入一座110 MW的储能电站,有效工作时间完全可以跨度用电高峰及低谷达26小时之久。2001年美国Ohio州和日本北海道空知郡先后投入2 700 MW和400 MW的机组。除了德、美、日外,以色列和韩国也在积极的开发压缩空气储能项目[1]。传统压缩空气储能储气罐多采用山洞、废弃的矿井等也容易造成选址不方便的问题,燃烧室的燃烧不充分也对环境不友好。目前,我国对压缩空气储能的研究多集中于传统的理论研究,着重于通过技术手段提高压缩空气储能的利用效率。文献[2]提出一种风光互补的压缩空气储能系统,利用风能的多余能效把能量以高压空气储存,利用太阳能进行释能前期的预加热,以减少对环境的污染和提高电能的输出。文献[3]利用海底恒压原理,将海洋能源和压缩空气储能结合。文献[4]在释能前期的预热处理采用熔融盐储热特性来为高压空气预加热,以提高系统储能效率。以上方法都在一定程度上提高了压缩空气储能的效率,但存在储能系统复杂、选址不易和对材料的要求极高的问题。
本文相较于传统的压缩空气储能在结构上进行了改变,巧妙地利用双液体罐液体对倒设计有效的减少了常规压缩空气存在的漏气和气体摩擦损耗的问题,故而提高了热转换效率使系统总的效率提高。该水动力压缩空气储能改变了传统的透平机发电方式引入了易于调峰调频的水轮机发电的技术,在传统压缩空气储能设备的基础上巧妙的利用了液体作为活塞,有效的减少了空气泄露,同时取消了燃烧室的设计,换用间冷蓄热/换热器,利用透平机排气做工的余热回收对下一轮压缩空气前管道进行预加热,在系统效率提高的同时兼具保护环境的优点。
1 系统主要原理及运行过程介绍
传统压缩空气储能主要有压气机、燃烧室、透平机、储气装置、发电机五个部分构成,如图1所示。在储能环节主要是将电能消耗掉用压缩机把空气压缩存储在储气室里,这个过程为绝热过程;释能环节打开储气室,高压空气从储气室进入燃烧室加热升温,此刻的空气变为高温高压的气体。这个过程为恒压吸热的过程。高温高压的空气迅速膨胀驱动透平机发电,这个过程为绝热膨胀过程。做工后的废气排出,温度下降,一个发电的循环过程结束。储能释能的不同步工作,释能时的压缩机没有消耗透平输出功率,使得其比传统的燃气轮机理论效率高达两倍。但是它结构中的燃烧室,依然会有化石燃料产生污染的问题,排出的废气在自然空气中冷却影响了系统效率,此结构对系统密闭性要求很高。
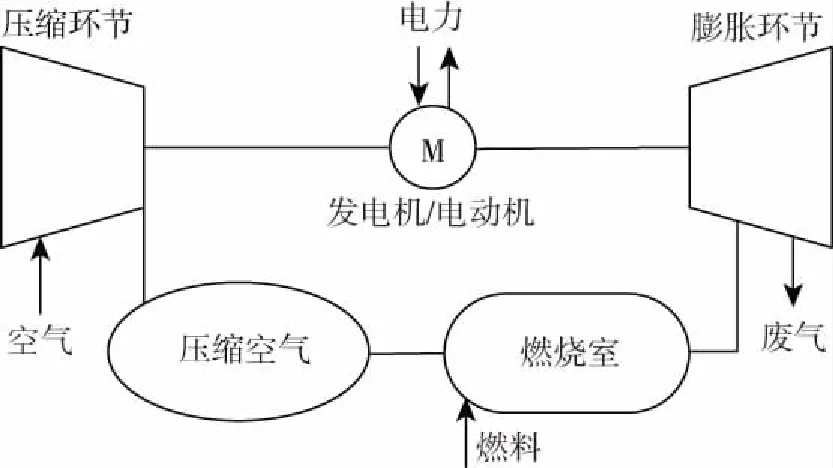
图1 传统压缩空气储能原理图Fig.1 Principle of traditional compressed air energy storage
针对以上问题,部分学者提出对传统的压缩空气储能结构进行改进,如图2所示。在图中可以看到该结构主要是在传统压缩空气储能结构中引进蓄热换热环节,此结构显著提升系统能量回收量,利用压缩过程中所释放的热量加热降压后的低压空气,缓解了对环境的污染。其主要过程为换热器采用液体储热,常温空气依次通过压缩机、换热装置进行降温,随后低温高压空气被存储在储气装置中;释能时,高压空气经过级前加热装置吸收压缩过程中的热量,而后进入透平膨胀做工,换热产生的热量可供下次循环使用[5]。图2所示的先进绝热压缩空气储能系统相较于图1传统压缩空气储能系统换热器的加入使得效率可以显著提高,但是储释能阶段气体泄漏和摩擦损耗问题一直未攻克从而在一定程度上影响了系统效率的进一步提高。

图2 改进型绝热压缩空气储能系统原理图Fig.2 Schematic diagram of improved adiabatic compressed air energy storage system
针对以上问题,本文提出一种新型的压缩空气水动力模型,引入了液体活塞,气体活塞技术用PLC作为控制单元实现了液体阀门开度控制,在此基础上对系统控制进行了优化,以提高系统压缩效率[6]。图3为压缩空气水动力储能系统改进部分截面图,如图所示,该结构电气驱动部分主要为液体泵、电磁阀门、控制单元,热力学转换部分主要是高压气罐、高压管道、液体罐(2个)、换热单元。图中的发电机改用水轮机,它有着转子短粗、机组的启动迅速、运行调度灵活、适用于调峰机组和备用机组的优势。基于以上优势,压缩空气储能系统可以更好的执行电力储能过程中“削峰填谷”的任务。
水动力压缩空气储能系统储能阶段,阀门6为入气口,阀门1、阀门3和阀门5关闭,阀门2和阀门4打开。当常温空气通过阀门6进入液体罐1时,打破了原来液体罐1和液体罐2 中水位平衡。空气在液体罐1中充当气体活塞压缩液体罐1中的液体经管道通过阀门4后汇入液体罐2中。液体罐2中液体反向充当液体活塞的作用,推动其原本存在的空气经阀门2后流经热交换器后存储在储气罐中。其中储气的体积取决于液体罐2中空气的体积,当液体活塞顶部到达液体罐2顶端时,储能阶段结束,关闭阀门1和阀门2.原则上为了实现储能容量的最大,可以在储能阶段开始之前,将液体罐中1液体装满,液体罐2中液体最少。
水动力压缩空气储能系统释能阶段,该阶段可以有两种方法实现释能。第一种方法为,阀门2、阀门3和阀门5打开,阀门1和阀门4关闭。
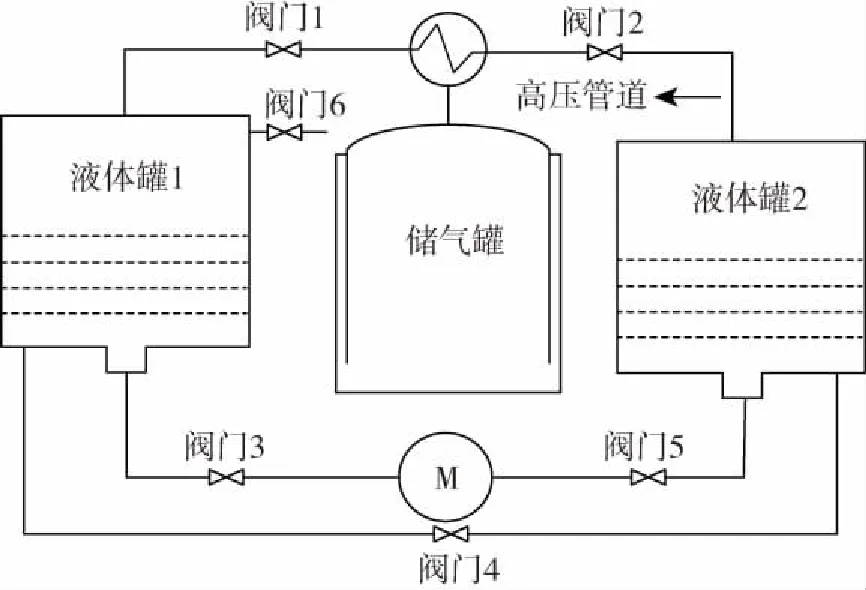
图3 水动力压缩空气储能系统单透平机截面图Fig.3 Section diagram of single turbine for hydrodynamic compressed air energy storage system
此阶段,经过加压保存的空气经过热交换器,通过阀门2所在的管道进入液体罐2中充当空气活塞,推动液体罐2中的液体流经阀门5所在的管道进入水轮机M做工发电。发电后的液体经过阀门3所在的管道进入液体罐1中。为了保证液体罐1中的维持常压,需要在液体罐1中加入泄压阀(阀门6),这样就可以减少液体罐1中压力增大引起的发电机效率减少。还有一种方法为阀门1关闭,其余阀门都打开。在这个过程中,储气罐中加压的空气,可以通过阀门2进入液体罐2中充当空气活塞,推动液体罐2中的水分别流经阀门5、发电机M和阀门3进入液体罐1中。此时阀门4及其所在的管道可以巧妙的充当液体罐1和液体罐2的稳压阀门。液体罐1中水可以通过阀门4返回液体罐2中,维持液体罐1和液体罐2中压强相当。
2 水动力压缩空气储能系统建模及算法优化
2.1 系统主要部件的建模
储能系统充放电过程是一个相对独立的过程,本文主要是通过对系统结构和控制算法进行优化进而提高其放电效率[7],故主要对其放电过程进行着重建模,模型主要有①转速控制环节;②阀门控制环节;③液泵;④储气罐。
在转速控制环节中,对于压缩空气储能可以在大范围转速透平发电,当输出功率一定时,总存在一个最优转速,这样可以实现以最小空气压力发电达到功率给定值。所以,在转速控制环节通过功率给定值计算出最优转速ωout作为发电机转速可以实现功率最优。功率给定值p与最优转速近似可以看做二次关系,即:
Wout=a1p2+a2p+a3
(1)
式中的参数可以通过透平厂家给出的参数得到,通过式子(1)计算出电机最优转速ωout与测得的电机实际转速ω差值,通过比例积分环节进行速度控制,计算出阀门控制环节输入信号m.
在阀门控制环节中,高压空气从储气罐流出经过解压阀解压才能流过液体罐用于推动透平做工。解压阀开度的调节,可以有效的控制管道中气体的压力和发电机的转速。气体通过换热器动态模型可以用一阶惯性表示,阀门控制环节主要输出气体压力信号,其约束条件为:
(2)
式中:pliu为液体压力;qliu为液体质量;m为阀门控制量;q为泵流量。
液泵是水动力压缩空气储能装置能量转换关键部分[8],其约束条件为:
(3)
式中:p为终端压差;T为输入转矩;ω为转速;D为泵容积;klou为露系数;kHP为哈泊系数;ηv为泵积效率;ηlv为泵效率;vf为流体运动黏度;ρ为液体密度;pk为泵额定压力;ωK为泵额定转速;vnom为额定流体运动黏度。
高压气罐是储能系统发电的动力源,气体压缩是用液体作为活塞实现的。假定工作在恒温压缩状态下,采用空气液体压缩原理,一个周期内约束条件为:
(4)
式中:Cr=pf/pair;pair空气实际压力;qair为液体罐流量;pa为大气压;pf为目标压力;K为多变指数;PJC为压缩效率。
2.2 压缩空气储能效率优化控制
系统效率的优化控制的目标就是在给定输出功率的需求前提下,系统以最大效率点运行。系统的输出功率和需求功率分别作为系统优化条件的两个极值,优化的目标就是寻找系统效率的最大值[9]。寻找极值的众多种方法中,拉格朗日乘子法在数值分析的领域中被用作解决此类问题。它可以在简单部件建模基础上引入拉格朗日乘子作为上下极值的约束条件。在不考虑系统弃功的情况下,系统效率最大值出现的条件就是给定功率约等于输出功率,可以表示如下,
(5)
也可以表示为pout-pxu=0,式中Pout为系统输出功率,Pxu为系统需求功率。根据系统效率和w函数构造拉格朗日函数,表示为:
Q(w,n,ρ)=η(w,n)+ρW(w,n)
(6)
式中:ρ为拉格朗日乘子;w为气体压力函数;n为发电机转速函数。式子中的Q函数是关于气体压力、发电机转速和拉格朗日乘子的三元函数,求解该函数的解即为系统效率的最优。
3 系统仿真及效率分析
水动力压缩空气储能系统是一个多变量非线性复杂系统,对系统直接建模是一个复杂的过程,本文通过把空气的压力转化为空气流速来实现系统仿真。由于系统主要考虑到热力学效率变化,MATLAB软件中可视化Simulink模块中Scope可以较直观反应效率曲线变化。在实际生产中为了系统高效的运行通常会有一个比较高的总压比,单级压缩显然但不到高效的要求,所以本文采用压缩和透平的级数为3级,这样不仅可以提高系统储能压缩效率,而且可以在透平阶段有效的保护透平机,提高系统稳定运行工作时间[10]。图4是水动力压缩空气储能系统MATLAB软件Simulink仿真图。
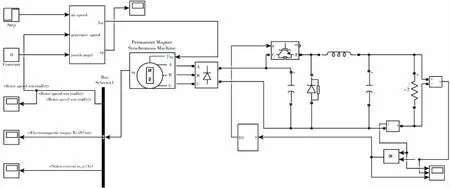
图4 压缩空气储能系统Simulink仿真图Fig.4 Software simulation diagram of compressed air energy storage system
图5、图6为透平初温为408 K、储气压力为1.2 MPa时,系统储能密度和体积随透平效率变化的规律。可以明显看到储能密度和总储气罐体积受透平效率影响较大。
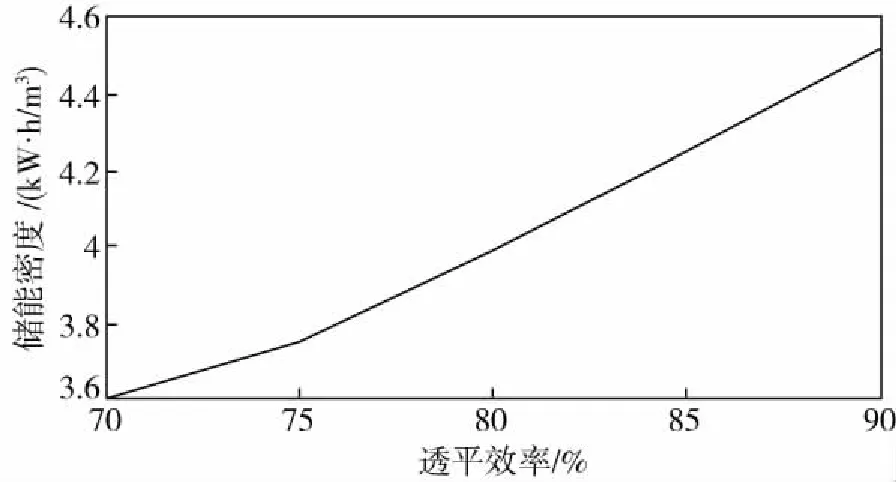
图5 储能密度对透平效率影响Fig.5 Effect of energy storage density on turbine efficiency
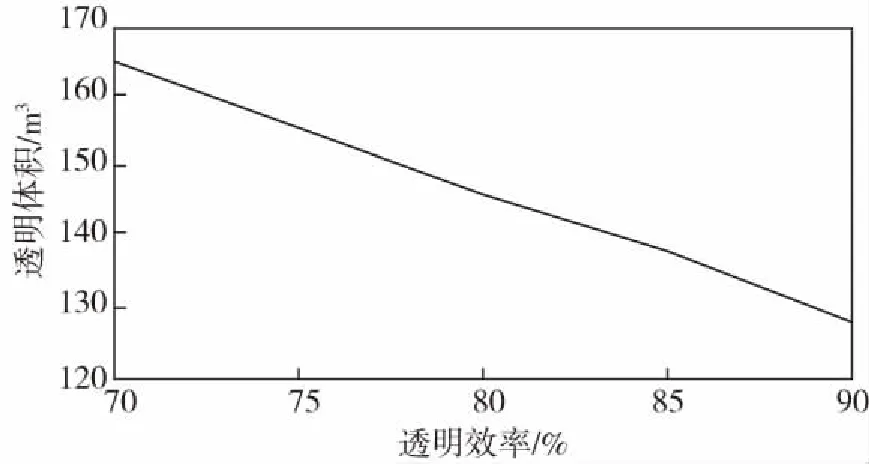
图6 总储气罐体积对透平效率的影响Fig.6 The influence of total tank volume on turbine efficiency
取透平机工况效率70%到90%,储能密度从3.6 kW·h/m3增加到4.52 kW·h/m3,增加了25%,透平效率从70%到75%影响略小。总储气罐体积从165 m3减小到128.7 m3,减小了22%.
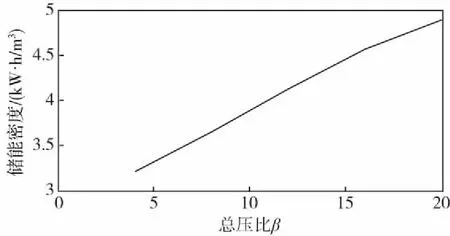
图7 总压比对系统储能密度的影响Fig.7 The influence of total pressure ratio on energy storage density of the system
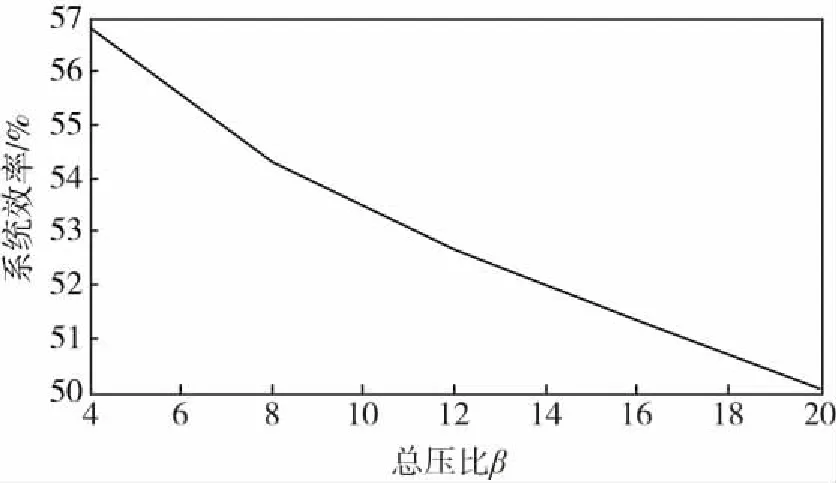
图8 总压比对系统效率的影响Fig.8 Effect of total pressure ratio on system efficiency
图7、图8为压缩效率为80%,透平机效率为85%条件下,系统效率和系统储能密度(kW·h/m3)随总压比的变化曲线。可以看出随着总压比的增长,储能密度成线性增长,这是因为总压比增长使得系统将空气压缩到较大的压强。但是也可以看到随着总压比的增长,系统效率随之减少,在初段减少的幅度要大于在尾段,这是因为随着总压比的增强系统的热损会加大,达不到理想状态的压缩膨胀效率[11]。传统压缩空气储能系统的效率为50%到55%,在图6可以看出改进型水动力压缩空气储能系统效率提高1.3%到1.8%,效率有所提高。
图9为是在压缩效率为80%、透平效率为85%,系统储能容量为230 kW条件下系统储能密度随压力与透平初温的变化曲线,图中从上到下依次表示储气室气压等级为1.5 MP、1.1 MP、0.7 MP和0.3 MP时储能密度随透平初温的变化曲线。由图9可知,透平初温和储气室气压对系统储能密度影响,当透平初温为303 K时,储气室气压由1.5 MP下降到0.3 MP,储能密度下降了0.7 kW·h/m3;当储气室气压保持不变时,储能密度随透平初温的增加而上升,假设储气室气压恒为1.5 MP,当透平初温由303 K上升到383 K时,储能密度增加了1.99 kW·h/m3.
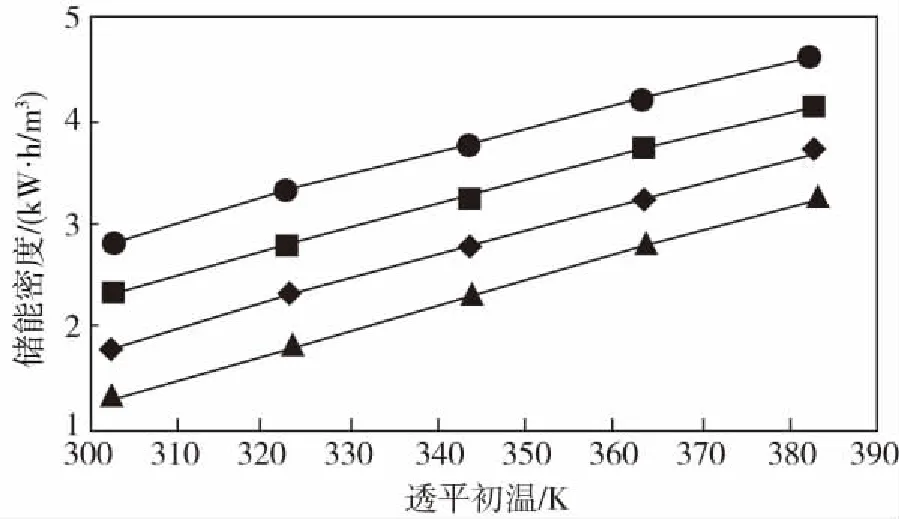
图9 储能密度随透平初温的变化曲线Fig.9 Change of energy storage density with turbine initial temperature
显然透平初温相比于储气室压力对系统储能密度影响的作用更大[12],验证了本文中在压缩机和透平机中间加入热交换器的合理性。
4 结论
本文是在传统的压缩空气储能系统的基础上,针对传统的压缩空气储能系统空气泄露,污染环境的问题[13],对系统的释能部分结构进行了改进,利用了液气循环水动力的方式进行储释能。通过仿真分析可得,本系统比传统的压缩空气储能系统效率提高1.3%到1.8%,且引入的热交换器提高系统储能密度,对小容量压缩空气储能开发具有广泛的应用前景。

