机械结构三维CAD模型姿态调整方法研究*

徐赐军

(湖北理工学院 机电工程学院,湖北 黄石 435003)

0 引 言

随着三维CAD模型在数量及复杂性上的极速增加,三维CAD模型的重用问题日益突出。

三维模型相似性评价是模型重用技术的关键指标,其预处理常常采用模型姿态调整。万丽莉[1]采用模型法线分布特性分析和归类,提出了一种基于模型表面法线分布特性的主成分分析法,实现了模型姿态调整旋转主轴的选取。朱新懿等[2]利用局部对称长度比来度量三维模型的局部对称性,实现了三维模型的对齐。SFIKAS K等[3]利用三维模型旋转和反射对称参数的计算确定了3D模型的对称平面,计算了模型的第一主轴,然后通过计算模型的像素值方差构建其他主轴,实现了三维模型检索过程中的姿态归一化处理。JOHAN H等[4]基于粒子群优化方法寻找最小投影面积,并依次确定了第一主轴和第二轴,提出了基于最小投影面积的姿态归一化方法。

目前,姿态调整方法在大多数情况下通用且性能良好,但无法捕捉到三维模型的某些特定特征。

三维模型形状描述子的基础特征主要包括统计特征和骨架特征[5]。统计特征主要以曲率、面积、距离、角度和法向量等为统计信息。张艺琨等[6]融合ORB特征和形状上下文特征提出了一种基于多特征融合的三维模型检索方法。

基于统计学的模型相似性评价原理简单明了,计算快速,但对于复杂的三维模型区分效果欠佳。骨架特征描述是结构特征简化的有效途径,在三维模型相似性研究中也得到越来越多的应用。朱文博等[7]利用模型骨架转化获得模型的拓扑结构信息,采用空间离散曲线的曲率和佛朗内特标架等方法计算骨架形状相似度。基于骨架的相似性评价对原始模型的信息要求比较严格,推广应用难度较大。

三维CAD模型具有清晰的解析表达式,可以利用空间解析几何等专业知识分析基本体的拓扑关系、几何尺寸等特征信息,获取机械结构基本体形态,并通过知识融合技术提取机械结构形态[8]2860-2862。因此,机械结构基本体形态作为机械结构相似性评价的形状描述子,可以克服统计特征和骨架特征的不足。

为了量化机械结构基本体形态的形状、尺寸、拓扑等特征,本文重点研究机械结构基本体形态的信息量度量方法,并基于机械结构形态提出三维CAD模型的姿态调整方法。

1 机械结构基本体形态

机械结构基本体形态是机械结构形态的基本组成单元,主要通过基本体转换模型的扫掠基面、扫掠导线和轮廓约束线三要素,分析选取其中某一要素或与其相关的线、面,作为基本体抽象描述的表达方式[8]2859-2860。

圆柱体的基本体模型和基本体形态如图1所示。

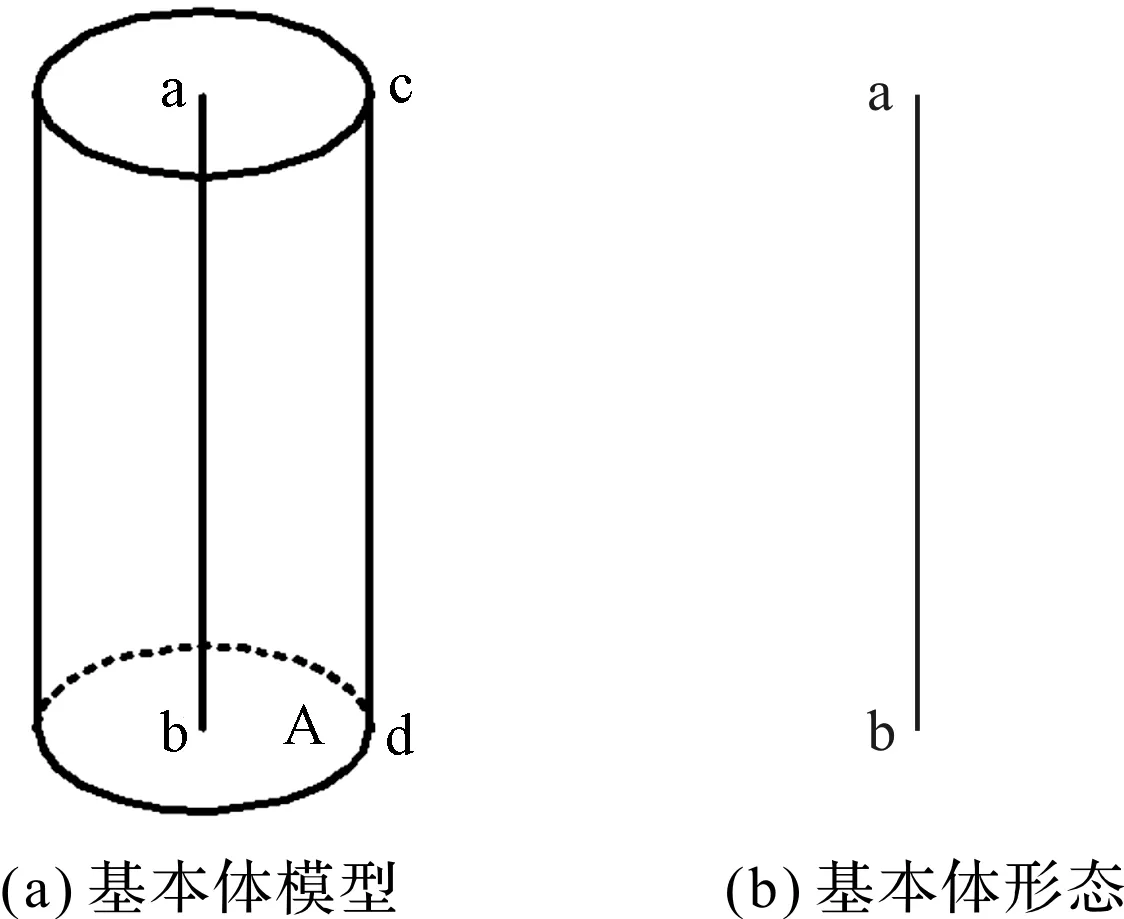
图1 基本体

根据机械结构三维建模过程中的基本体布尔运算关系,将基本体形态进行知识融合,则可构建机械结构形态[9]2193-2196,如图2所示。

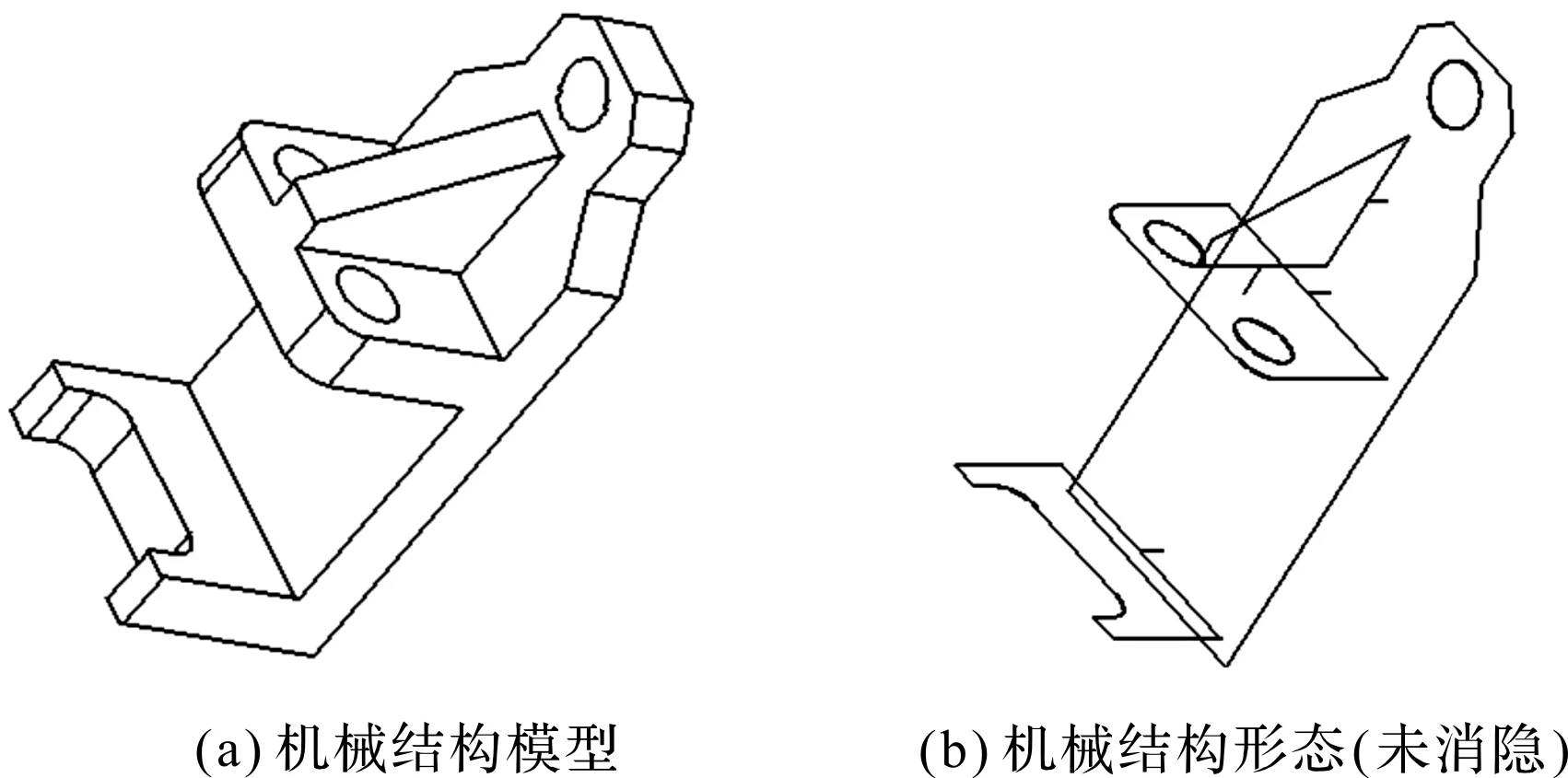
图2 机械结构

基本体形态具有确定的解析表达式,便于三维模型的变换和空间特征计算。因此,机械结构三维模型的姿态调整可以充分利用机械结构基本体形态的表达和变换特性。

基于机械结构形态的三维CAD模型姿态调整算法框图如图3所示。

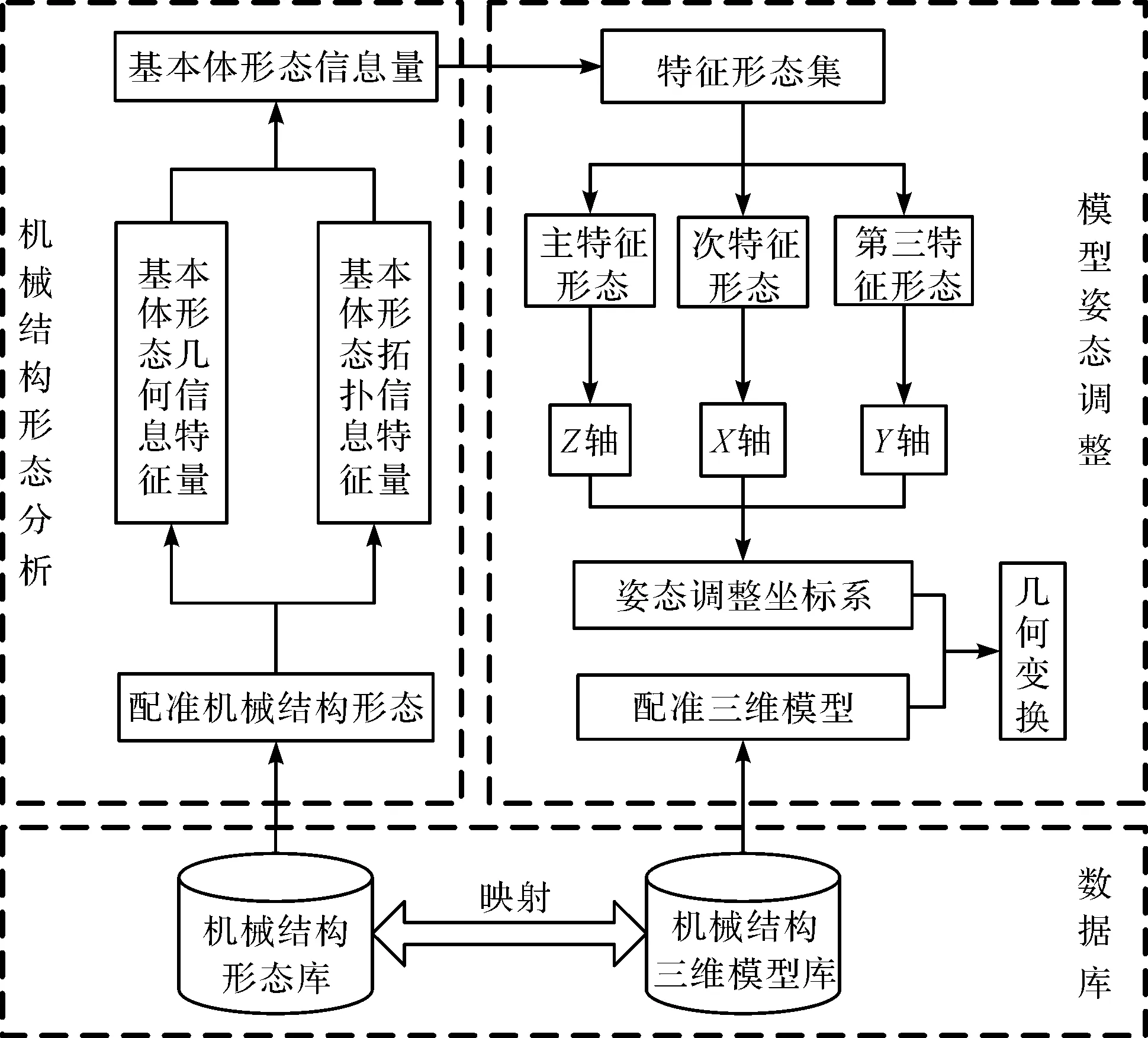
图3 姿态调整算法框图

图3显示了机械结构形态分析模块量化基本体形态信息量,并基于该信息量确定机械结构的主特征形态、次特征形态以及第三特征形态,从而可以构建三维模型姿态调整坐标系,实现机械结构模型的空间几何变换。

2 基本体形态信息量

根据基本体建模时是增加实体还是移除材料,笔者将基本体形态分为增材基本体形态和减材基本体形态。减材基本体必须依附于增材基本体,所以三维模型相似性比较只选择增材基本体形态;若根据基本形态的几何要素及曲线封闭情况,则可将基本体形态分为开环线形态、闭环线形态和面形态。

2.1 当量线形态

机械结构形态主要由基本体线形态和基本体面形态构成。对于一个面要素,其空间信息主要通过其几何形态来反映[10]。为了实现它们之间信息量的可比性,本文将面形态转换成几何信息量相当的线形态,定义为当量线形态;若面形态存在多个闭环形态,则取其最大轮廓形态为比较形态[8]2862。

假设第i个基本体面形态的轮廓周长为li,则将该面形态转换成等周长的圆形面,即转换形态的直径为li/π。对于转换后的形态各方向最大值均为li/π,而根据文献[8]2862的机械结构形态提取方法可知,当扫掠基面各方向的最大值为La,且该基面对应的扫掠导线长度为Lc时,面形态应满足Lc<2.618La。

因此,令面形态的扫掠导线最大值Lc=2.618La,则该面形态转换成当量线形态时,其周长为Lc,且La=li/π。

因此,第i个基本体面形态的当量线形态周长为:

ci=2.618×li/π≈0.83li

(1)

2.2 基本体形态信息量量化

机械结构形态既体现了基本体的几何特征,又反映了基本体的拓扑关系,因此基本体形态信息量是基本体形态几何信息和拓扑信息的度量,且论域为同一个机械结构形态的基本体形态。根据式(1)将面形态转换成线形态后,笔者通过计算基本体形态信息量,即可比较每个基本体形态特征的重要性,从而识别机械结构形态中主要特征的基本体形态,即特征形态。

(1)线形态几何信息特征量

基本体线形态的几何信息主要包括尺寸和曲线弯曲次数,且尺寸越大、弯曲次数越多,该形态特征的不确定性越小,即所载的几何信息量越小。基本体线形态尺寸信息特征量Ici定义为第i个基本体线形态的周长ci与机械结构形态中所有基本体线形态总周长c之比,即Ici=ci/c;基本体线形态弯曲信息特征量Ibi定义为基本体线形态线段数mi与机械结构形态中所有基本体线形态总线段数m之比,即Ibi=mi/m。

(2)基本体形态拓扑信息特征量

基本体拓扑关系反映了基本体之间的连接属性,若基本体形态关联的形态数量越多,则说明该基本体形态在机械结构形态中的作用越大。基本体形态拓扑信息特征量Iti定义为第i个基本体形态关联的基本体形态总数ni与机械结构形态的基本形态总数n之比,即Iti=ni/n。

(3)信息量计算

根据信息量的定义,对尺寸信息特征量、弯曲信息特征量和拓扑信息特征量取对数,即可得到每个特征的信息量。由于尺寸特征量、弯曲特征量和拓扑特征量相互独立,且基于各特征量在信息贡献上的重要性考虑,在各特征信息量合成过程中采用加权和的方法。

因此,第i个基本体形态信息量表示为:

(2)

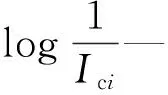
若取对数底数为2,则基本体线形态几何信息量单位为bit。

当基本体形态为面形态时,基本体线形态尺寸信息特征量中的周长ci表示当量线形态周长,基本体线形态弯曲信息特征量中的线段数mi表示面形态轮廓的线段数。

3 姿态调整

在机械结构形态中,笔者根据基本体形态信息量从小到大的顺序,依次将信息量最小的3个基本体形态分别定义为机械结构形态的主特征形态、次特征形态和第三特征形态,并以此为依据,构建机械结构三维CAD模型姿态调整坐标系的轴。若基本体形态为开环线形态,则特征向量为基本体形态起点指向终点的向量;若基本体形态为闭环线形态或面形态,则特征向量为基本体形态所在面的法向量,其方向根据几何元素数据存储顺序及右手定则确定。

此处令主特征形态、次特征形态和第三特征形态所对应的特征向量分别为v1、v2、v3,且闭环线形态和面形态的特征向量起点为其形心;另令分别过v1、v2、v3的起点,且分别以其相应向量为方向向量,构建的直线为L1、L2、L3。

机械结构三维模型姿态调整坐标系的构建步骤如下:

(1)以v1起点为坐标系原点,直线L1的位置为Z轴;

(2)由原点分别指向次特征形态、第三特征形态的特征点构建向量u2、u3,依次以Z轴上单位向量与u2、u3的夹角小于90°为判断条件,直至确定Z轴正向为止。若v1与u2、u3均垂直,则说明次特征形态、第三特征形态的顶点在Z轴正负方向分布比较均匀,因此,此时选择v1的方向为Z轴正方向;

(3)过原点构建Z轴的垂直面。当L2与L1、L3均共线时,在垂直面内过原点构建X轴,且依次以系统坐标系下的向量(1,0,0)和(0,1,0)与X轴正向向量夹角最小确定X轴位置和方向;当L2与L1共线且与L3不共线时,在垂直面内以n2=v3×v2为方向向量过原点构建X轴,且取X轴上向量与u3的夹角小于90°的方向为X轴正向,否则取n2方向为X轴正向;当L2与L1不共线时,以n3=v1×v2为法向向量过原点构建平面,该平面与垂直面的交线为X轴。当X轴方向没有确定时,依次以X轴上单位向量与u2、u3、v2、v3的夹角小于90°为判断条件,直至确定X轴正向为止;

(4)根据右手定则确定Y轴的位置和方向。

上述步骤若不存在次特征形态或第三特征形态,则涉及该形态的判断不执行,且将仅有主特征形态的情况视为L2与L1、L3均共线。

根据机械结构三维模型姿态调整坐标系,以查询机械结构三维模型的姿态调整坐标系为参照,将待比较机械结构三维模型姿态调整坐标系进行变换,使两者坐标系重合。因此,笔者先根据两个姿态调整坐标系的几何关系,直接求解三维模型做平移归一化、旋转归一化的姿态调整参数,而比例归一化处理的缩放因子则需根据待比较的两个机械结构形态的几何尺寸进行选取,且以查询机械结构形态为基准。最后根据空间几何变换技术即可实现三维CAD模型的姿态调整。

4 实例验证

机械结构三维CAD模型具有清晰的建模过程,且基本体具有明确的解析表达式。

机械结构三维模型如图4所示。

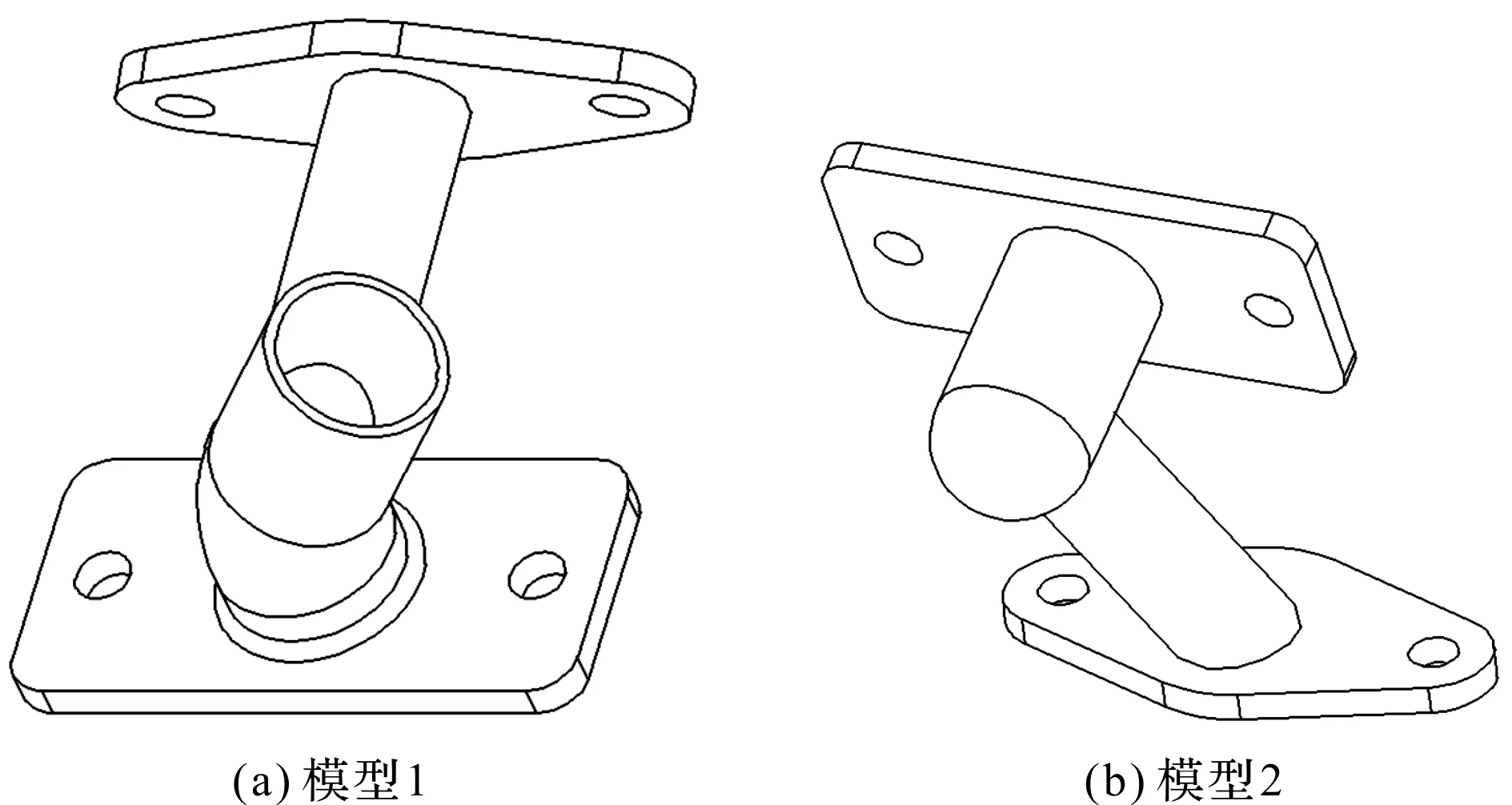
图4 机械结构三维模型

图4中,两个模型结构相似,但建模时造型步骤不一样导致其空间位置不同,不利于两个模型的相似性比较。因此,本文采用基本体形态信息量度量方法确定模型的主要特征结构,以利于模型的相似性比较。

针对三维CAD模型的构建特征,笔者获取两个三维模型对应的机械结构形态如图5所示。

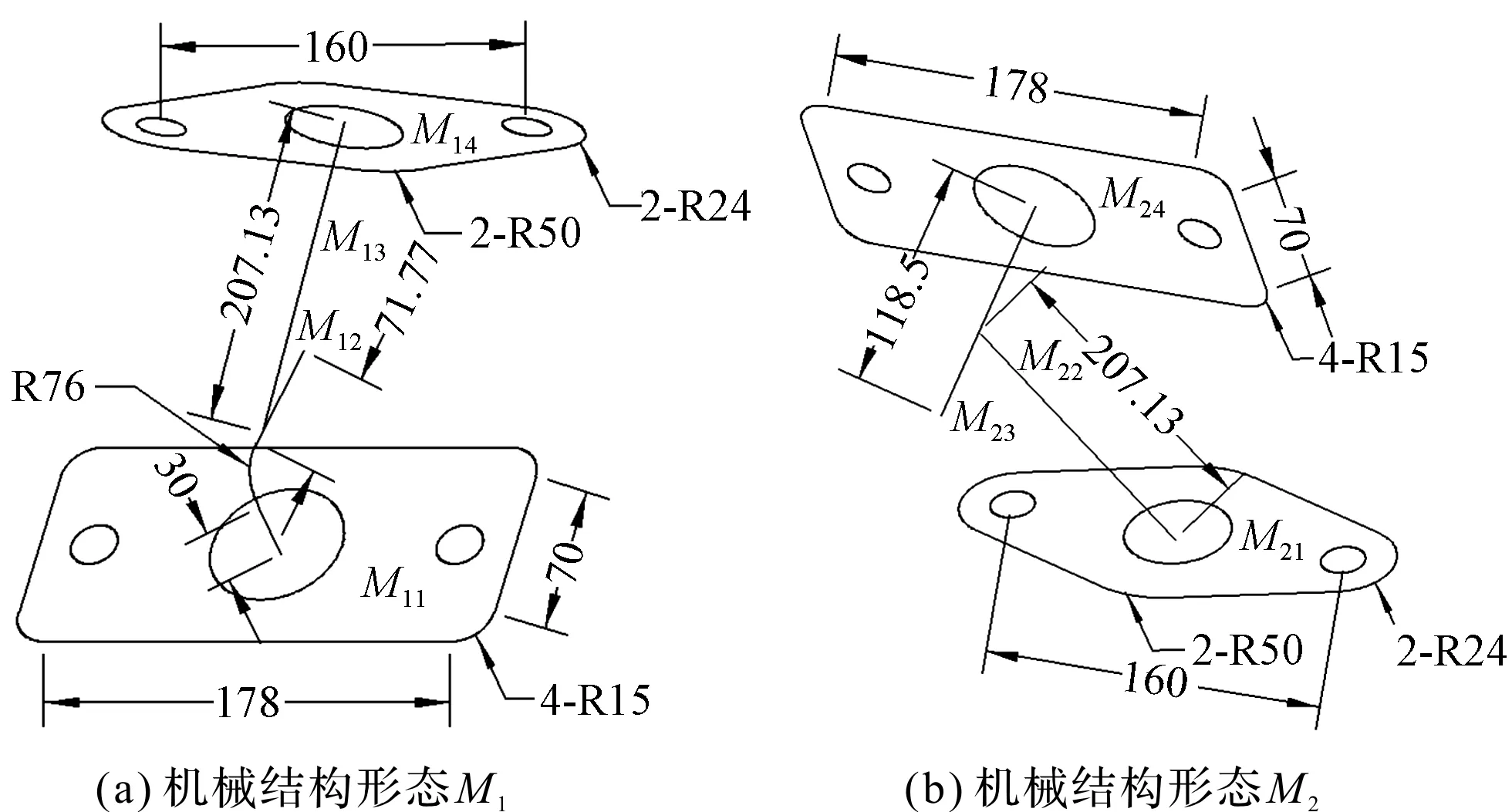
图5 机械结构形态

图5中,机械结构形态模型数据采用顶点为基础的数据结构予以存储[9]2198,且经顶点数据转换后几何尺寸如图5所示。

根据机械结构形态提取方法,由图5可知:两个模型均含有4个基本体形态,即M11、M12、M13、M14和M21、M22、M23、M24,其中M11、M14、M21、M24为面形态,其余为线形态。

根据本文机械结构基本体形态信息量度量方法及图5所示结构和几何尺寸,可得到基本体形态的信息量参数,如表1所示。

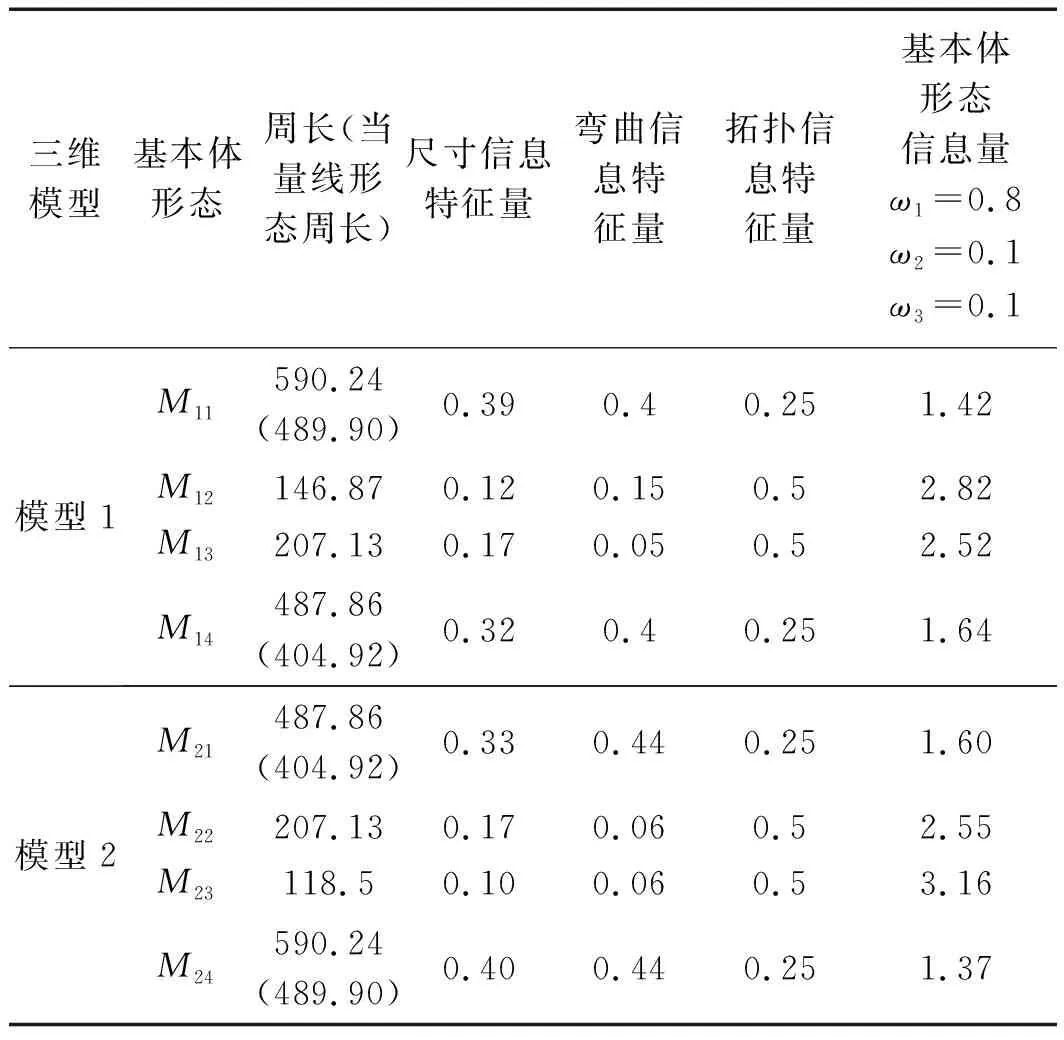
表1 基本体形态信息量参数

根据信息论可知信息量越小基本体形态不确定性越小,则由表1的基本体形态信息量可确定:模型1、模型2的主特征形态、次特征形态和第三特征形态分别为M11、M14和M13,以及M24、M21和M22。

根据模型1、模型2的特征形态以及机械结构三维模型姿态调整坐标系的构建步骤,可获得各自的三维模型姿态调整坐标系,如图6所示。

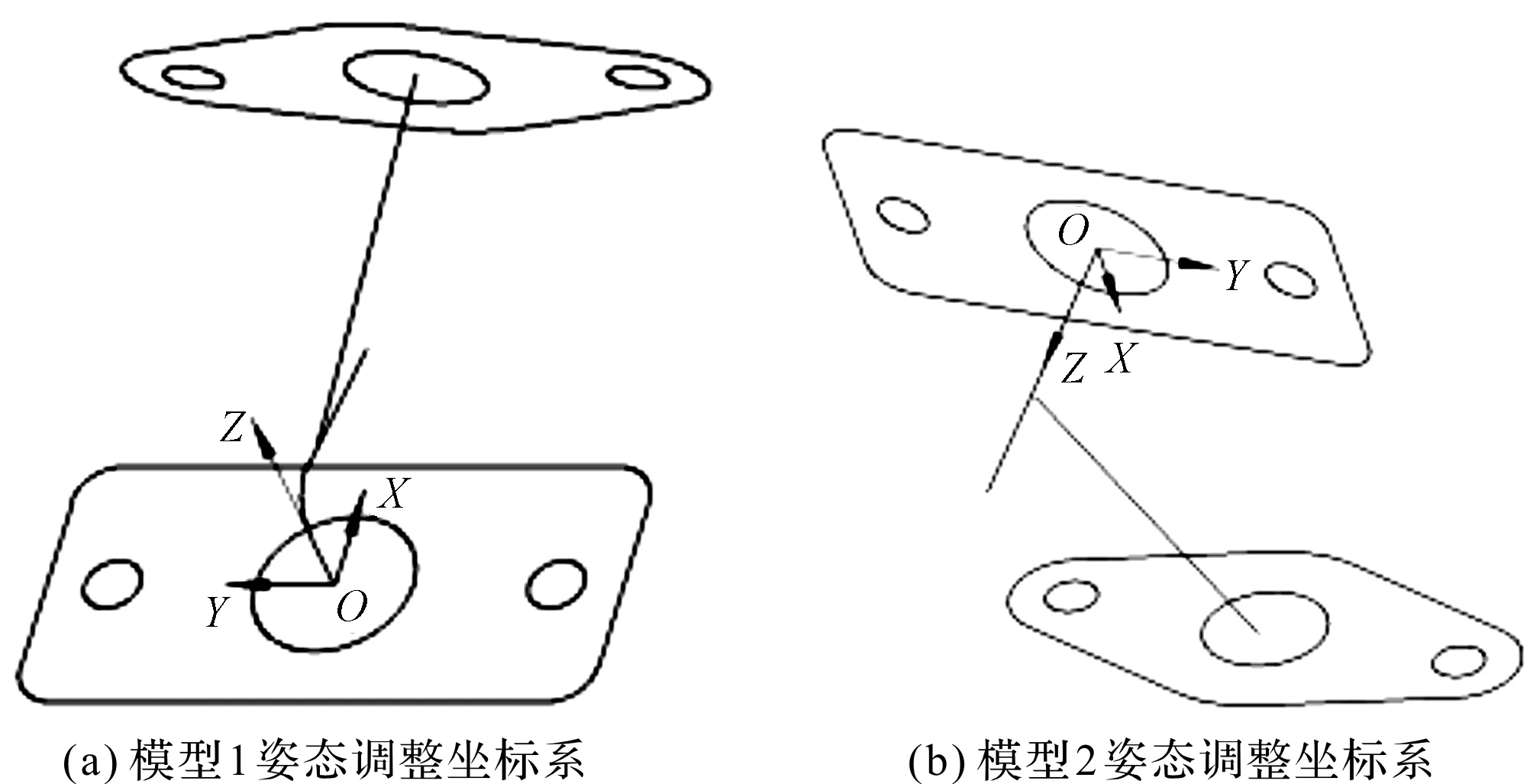
图6 三维模型姿态调整坐标系

以模型1的三维模型姿态调整坐标系为参照,通过空间几何变换技术可获得模型2新的空间姿态,如图7所示。

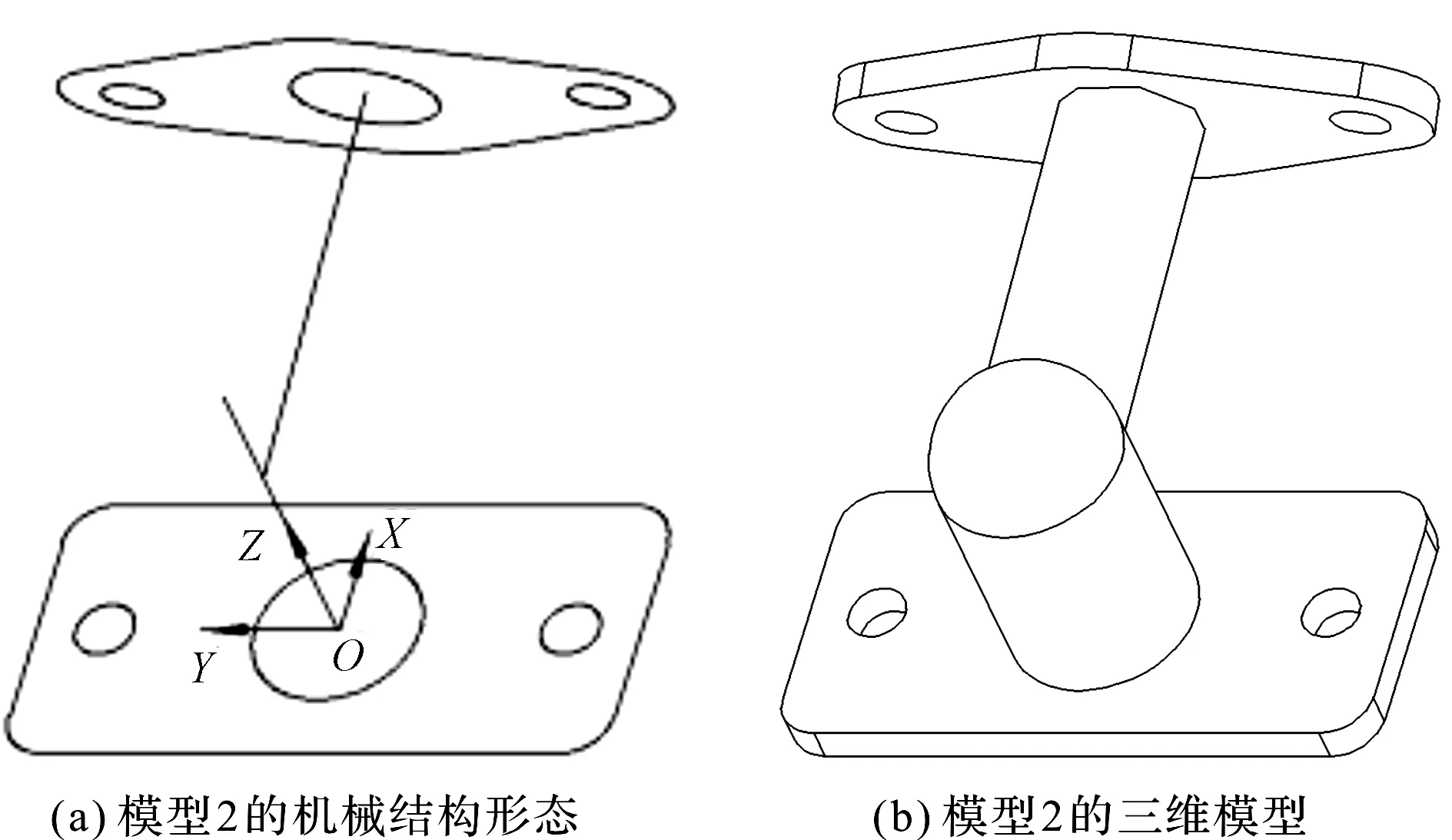
图7 姿态调整后的模型2

由图7(b)及图4(a)可知:经变换后,两个模型空间姿态更加相似。

5 结束语

针对机械结构基本体形态可以反映三维模型每部分结构的尺寸、形状和拓扑关系等特征,本文提出了一种基于机械结构基本体形态的三维CAD模型姿态调整方法。

首先针对机械结构基本体形态的特点,采用当量线形态技术处理异构的基本体形态;并研究了基本体形态的几何信息特征量、拓扑信息特征量,提出了基本体形态信息量的计算方法,实现了机械结构三维模型的主要特征结构的识别;基于机械结构特征形态提出了三维CAD模型的姿态调整方法,并通过实例验证了该方法的有效性。

研究结论表明:机械结构基本体形态信息量度量方法可以有效简化机械结构三维模型的相似性比较过程,为三维模型姿态调整等技术提供新的方法。