基于非支配排序遗传算法的核动力堆中子-γ混合射线屏蔽智能优化
毛 婕,宋英明,*,张泽寰,杨 力,韩 嵩,赵 均
(1.南华大学 核科学技术学院,湖南 衡阳 421001;2.中广核研究院有限公司,广东 深圳 518026)
在反应堆屏蔽设计中,由于中子和γ射线与物质相互作用原理不同,屏蔽所需的材料也不相同。另外,中子在与物质发生相互作用的过程中会产生次级γ射线[1-2],因此在设计中要考虑中子-γ混合辐射场的综合屏蔽效果。
对于船用反应堆这类特殊用途的反应堆,在屏蔽设计中,不仅需关注人员以及环境所受到的辐射剂量,还须对反应堆的重量和体积进行优化设计[3]。设计人员总是期望在满足剂量限值的条件下,得到体积小、重量轻且屏蔽效果好的屏蔽设计方案[4]。以往的多目标问题通过加权等方式转换为单目标问题,再利用数值方法进行求解,这样的求解方法效率太低且对于权重的设置十分敏感。遗传算法可有效解决上述问题,而基于精英策略的非支配排序遗传算法(NSGA-Ⅱ),对比一般遗传算法,增加了拥挤度比较算子以及快速非支配排序的应用,具有计算复杂度低以及不需指定共享参数等特点,性能更全面和优越[5-7]。
本文以萨瓦纳船用核动力堆为原型,建立核动力堆中子-γ混合辐射场计算模型,利用屏蔽智能优化方法进行屏蔽参数的多目标优化,得到一系列pareto最优解。为验证寻优结果的可行性,选取其中1组最优解,将蒙特卡罗方法计算和神经网络预测得到的剂量率进行对比,以验证该屏蔽智能优化方法的可行性。
1 屏蔽智能优化方法
本文利用的屏蔽智能优化方法是一种基于神经网络和NSGA-Ⅱ的优化方法,能快速、智能地对屏蔽参数进行优化[8],该优化方法主要由蒙特卡罗自动计算、神经网络计算、遗传算法(NSGA-Ⅱ)寻优3个模块组成。首先由蒙特卡罗自动计算模块根据设定的屏蔽模型计算得到一定数量的数据样本;接着由神经网络模块对数据样本进行学习训练,直到数据预测误差满足要求;最后将神经网络预测的数据样本作为遗传算法适应度函数的参数进行寻优计算,得到优化后的屏蔽参数,具体流程示于图1。
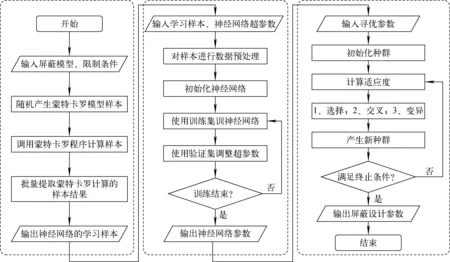
图1 基于神经网络和NSGA-Ⅱ的屏蔽智能优化方法流程图
2 核动力堆优化模型
2.1 计算模型
根据Kulvnvch[9]以及文献[3]中萨瓦纳船用核动力堆的相关设计参数,等比例建立多目标优化模型。考虑到反应堆结构的复杂性,对模型进行一定简化处理。上半部分由局部屏蔽层(铅层)以及二次屏蔽层和安全壳组成(图2)。下半部分由一次屏蔽层、二次屏蔽层以及安全壳组成(图3、4)。各部分模型由内至外的屏蔽材料以及厚度变化区间列于表1。
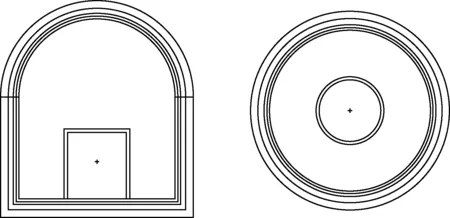
图2 核动力堆上部模型

图3 核动力堆下部一次屏蔽模型

图4 核动力堆下部屏蔽模型

表1 核动力堆模型屏蔽材料厚度区间
2.2 优化目标
根据辐射防护的基本任务[10]以及屏蔽设计的优化原则,将屏蔽结构的总重量以及屏蔽后的剂量作为优化目标,通过设置不同的约束条件进行寻优计算,在NSGA-Ⅱ中,使用约束条件可对种群中的个体进行筛选,从而确保优化方案满足约束条件。其中,目标函数[11-12]可表示为:
1) 双目标优化模型
(1)
其中:ρi为不同屏蔽层材料的密度;Vi为相应的屏蔽层体积;Fi为第i个能区的中子(或γ)的剂量率;约束条件为在j能区下剂量率Fj小于约束限值Lj(i≠j)。
2) 三目标优化模型
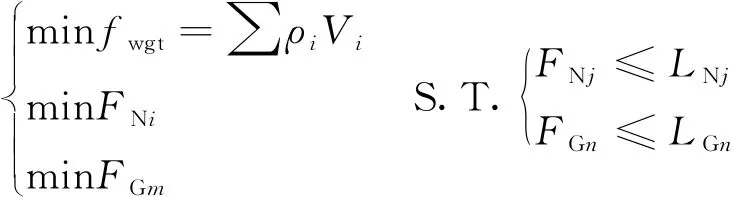
(2)
其中:FNi为该混合辐射场模型下中子能区i的剂量率;FGm为该混合辐射场模型下伽马能区m的剂量率;约束条件为在中子能区j和伽马能区n的剂量率分别低于其对应的限值LNj和LGn(i≠j,m≠n)。
3 核动力堆上部模型优化结果
3.1 神经网络训练结果
神经网络的数据样本通过本文所述的屏蔽智能优化方法中的蒙特卡罗自动计算模块生成。为保证计算结果的正确性,在生成数据样本前,使用厚度区间内的最大厚度代入蒙特卡罗模型进行计算,确保在该情况下计算结果的统计误差在2%以内,从而保证在抽样的厚度范围内样本的计算结果误差均小于2%。
上部优化模型共设置5个优化变量(屏蔽层厚度变量作为神经网络学习训练的输入数据)、8个输出剂量(作为神经网络学习训练的输出数据)。本文在保证样本均匀抽样的前提下,在相同的优化范围内分别生成3 000和60 000组数据样本进行神经网络的学习训练,表2为该模型的神经网络的训练参数,训练误差对比列于图5。
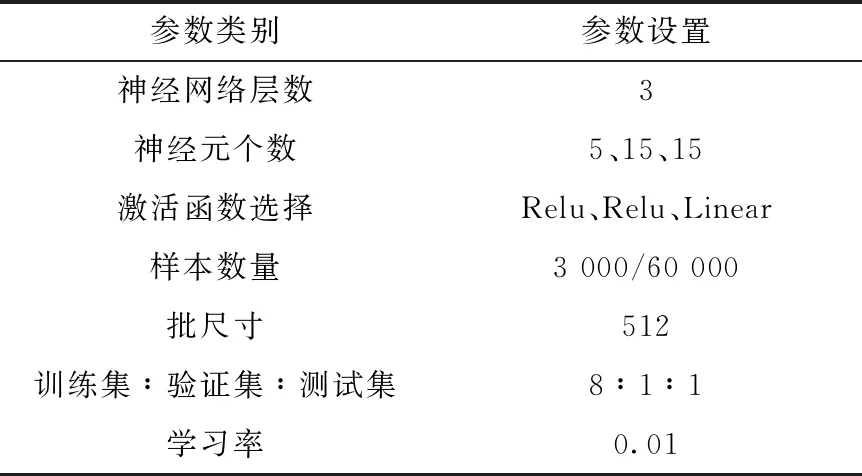
表2 核动力堆上部模型神经网络训练参数
结果表明,使用3 000组数据样本进行神经网络训练得到的误差结果与使用60 000组数据样本计算得到的结果相近,其平均绝对相对误差(mean absolute percentage error, MAPE)均在3%~4%之间。因此,对当前的问题而言,样本数量对于神经网络的计算结果影响不大,该类模型学习样本的输入输出变量之间相关性较好,在抽取的数据点有限的情况下,仍能通过较少的学习样本达到相近的泛化能力。因此,在本文的算例中,样本数量选择为3 000组,根据文献[13]中所述,在保证预测精度的前提下,也能在较大程度上减少有关蒙特卡罗模型的计算时间。
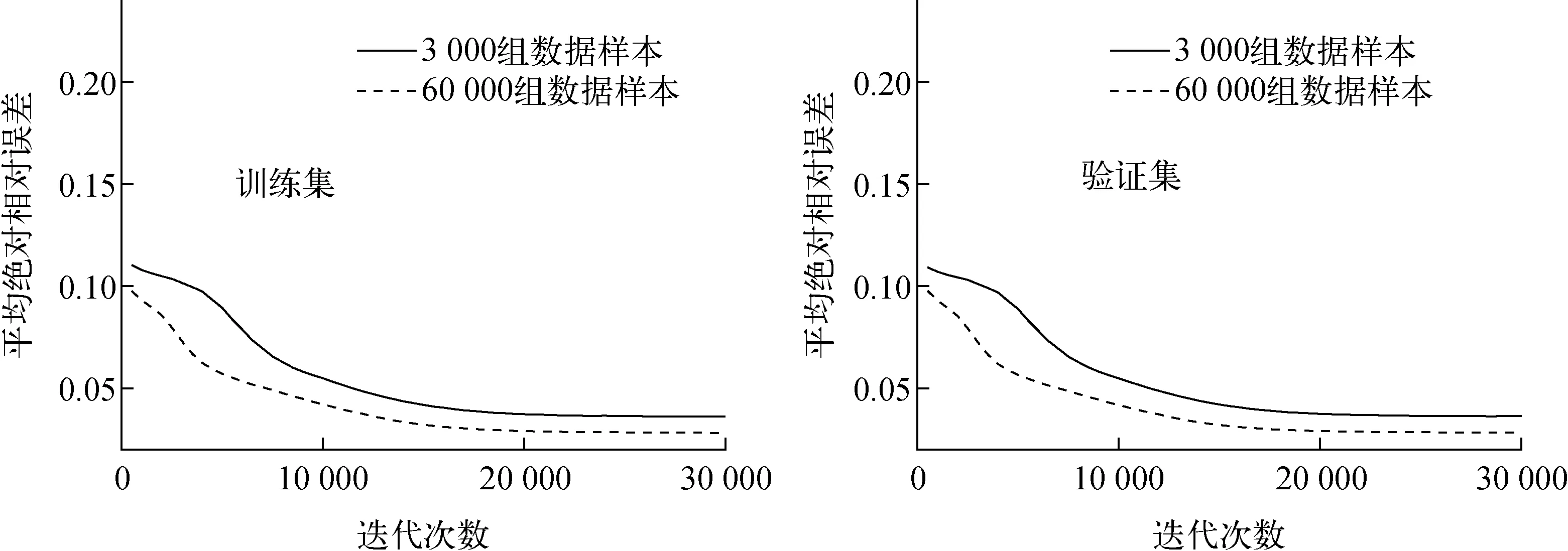
图5 核动力堆上部模型不同数量样本的神经网络训练误差对比
3.2 遗传算法寻优结果
结合神经网络预测的数据样本,设置遗传算法的约束条件为表3,种群数目设置为400,最大迭代次数设置为1 000,在表1给出的萨瓦纳上部屏蔽层的厚度区间内进行寻优计算。表3中,NR为中子径向面的能区,NA为中子轴向面的能区,GR为γ径向面的能区,GA为γ轴向面的能区。

表3 核动力堆上部模型不同能区剂量率限制条件
在优化问题为双目标的前提下,设置优化目标为屏蔽层总重量和屏蔽后的剂量率,在优化问题为三目标的前提下,设置优化目标为屏蔽层总重量、屏蔽后的中子剂量率以及γ剂量率。经过寻优计算后得到图6所示的pareto最优解前沿,图6中WNR为优化目标为屏蔽层总重量和中子径向面能区NR的剂量率;WNA为优化目标为屏蔽层总重量和中子轴向面能区NA的剂量率;WGR为优化目标为屏蔽层总重量和γ径向面能区GR3的剂量率;WGA为优化目标为屏蔽层总重量和γ轴向面能区GA3的剂量率;WNGR为优化目标为屏蔽层总重量、中子径向面能区NR和γ径向面能区GR3的剂量率;WNGA为优化目标为屏蔽层总重量、中子轴向面能区NA和γ轴向面能区GA3的剂量率。
图6显示,双目标寻优得到的最优解分布较均匀,少部分区域出现分布较稀疏的情况;三目标寻优只得到了少数的最优解。在高性能反应堆的屏蔽结构设计中,设计师们总期望在满足剂量约束限值的条件下,屏蔽体总重量越小越好[14]。因此,选取寻优计算得到的最优解中具有质量最小的1组解进行可行性验证,将其代入蒙特卡罗程序计算得到相应的屏蔽后剂量率(MC),同时与神经网络预测值(FCN)和寻优计算时的约束限值(UBs)对比,结果示于图7,图中Opti-O为优化目标。
图7显示,蒙特卡罗计算结果与神经网络预测值基本持平,且所有的剂量率均满足寻优计算时的约束限值。在双目标寻优中,优化后的屏蔽层总重量均减少了,在三目标寻优中,WNGR情况下的屏蔽层总重量略高于原始实际屏蔽层总重量。
4 核动力堆下部一次屏蔽模型优化结果
4.1 神经网络训练结果
该部分优化模型设置13个优化变量(屏蔽层厚度变量)、7个输出剂量(表4)。
根据表4的神经网络训练参数设置进行神经网络训练,得到神经网络训练误差如图8所示,其中训练集与验证集的MAPE收敛在4%以内,测试集上MAPE为3.918 2%,神经网络预测精度良好。

图6 核动力堆上部模型pareto最优解前沿

图7 核动力堆上部模型蒙特卡罗方法计算与神经网络预测输出剂量率对比
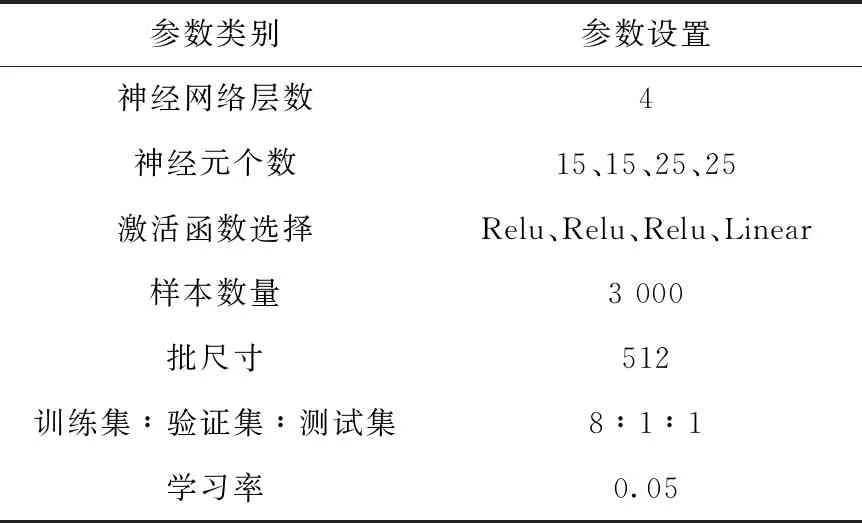
表4 核动力堆下部一次屏蔽模型神经网络训练参数
4.2 遗传算法训练结果
优化限制条件列于表5,在表1给出的萨瓦纳下半部分一次屏蔽层的厚度区间内进行寻优计算。设置遗传算法种群数目为400,最大迭代次数为1 000。
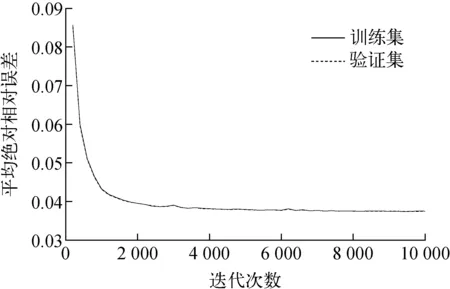
图8 核动力堆下部一次屏蔽模型神经网络训练误差

表5 核动力堆下部一次屏蔽模型不同能区剂量率限制条件

图9 核动力堆下部一次屏蔽模型pareto最优解前沿
经过遗传算法寻优计算后,得到pareto最优解前沿,示于图9。图9中,WN为优化目标为屏蔽层总重量和中子能区N4的剂量率;WG为优化目标为屏蔽层总重量和γ能区G3的剂量率;WNG为优化目标为屏蔽层总重量、中子能区N4和γ能区G3的剂量率。
图9中双目标寻优得到的pareto最优解分布均匀,三目标寻优只得到1组最优解。选取其中标注的最优解(总重量最小),利用蒙特卡罗方法计算和神经网络预测,得到图10所示的结果对比图。
图10显示,蒙特卡罗计算结果均与神经网络预测值持平,且大部分满足寻优计算时的约束条件,WG γ能区的结果中,能区G2的蒙特卡罗计算结果略超出了计算限值,通过计算得到该蒙特卡罗计算结果与神经网络预测值的MAPE为3.26%,与约束限值的MAPE为2.08%,在神经网络学习预测的误差范围内。
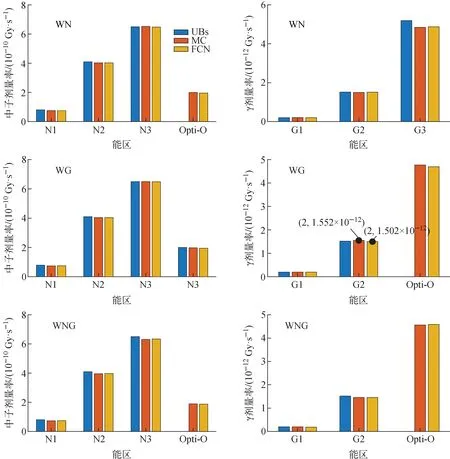
图10 核动力堆下部一次屏蔽模型蒙特卡罗方法计算与神经网络预测的输出剂量率对比
5 总结与展望
本文利用自主开发的基于神经网络和遗传算法的屏蔽智能优化方法,对核动力堆中子-γ混合辐射场的优化模型进行寻优计算,整个计算过程均自动完成。
由两个优化模型的计算结果可得,利用该优化方法进行双目标寻优可得到分布均匀的pareto最优解前沿,而对于求解三目标优化模型还存在一定欠缺,通常只能得到1个最优解。原因为: NSGA-Ⅱ使用的排序策略及拥挤距离比较方式存在一定的缺陷,导致最后的pareto解集出现收敛慢以及多样性差的情况[3];在使用NSGA-Ⅱ求解多目标优化问题时,随着目标函数数量的增多,非支配解的数量会呈指数增长,互不支配的可能性将急剧上升[15-17]。
另一方面,经过蒙特卡罗方法的验证,在神经网络预测误差允许范围内,无论是双目标还是三目标寻优,最后得到的最优屏蔽结构(重量最轻)在经过中子-γ混合射线辐射后,屏蔽后的剂量率均满足剂量约束条件,这说明得到的优化屏蔽参数是可行的,从而也验证了此屏蔽智能优化方法的可行性。
对典型的反应堆屏蔽问题而言,其中子和伽马射线的透射规律相近,具有相似的数据变化特征,因此,本方法适用于这一类混合辐射场问题。但不同模型的反应堆源项以及屏蔽层的几何形状、尺寸有较大差异,需针对不同模型计算产生不同的神经网络学习样本。综合本文得出的计算样本数量与神经网络预测误差的变化规律,计算的样本数量通常可控制在较小的范围内。因此与纯蒙特卡罗方法耦合遗传算法相比,其调用蒙特卡罗方法计算的开销较小,仍具有快速准确的特点,并能极大程度缩短优化时间。

