寻找解题的突破口

◎ 相堂奎

有些题目，乍一看比较麻烦，但仔细思考，认真分析，寻找出解题的突破口，就能使复杂问题迎刃而解。

例：有两桶水，第一桶水重是第二桶的，如果从第一桶内取出13千克水倒入第二桶，这时第一桶的水重正好是第二桶的。两桶水原来各重多少千克？

分析与解：题目中两个分率对应的数量都是第二桶的重量，乍一看相同。但第二桶的前后重量发生了变化，因此单位“1”也就发生了变化，不容易直接找出量率的对应关系，所以按照一般思路不易解答。

我们再仔细思考，发现从第一桶取出13千克水倒入第二桶后，虽然两个水桶里的水重量都发生了变化，但它们的总量没有变，因此可以把两桶水的总量看作单位“1”。由“第一桶水重是第二桶的”这个条件，可以把第二桶的水重看作9份，第一桶有这样的4份，两桶水的总重量相当于这样的4+9=13（份），第二桶水的重量就相当于两桶水总重量的。

由“从第一桶内取出13千克水倒入第二桶，这时第一桶的水重正好是第二桶的”，可以知道，如果把第二桶的水重看作10份，第一桶水就有这样的3份，第二桶水的重量相当于两桶水总重量的。所以，13千克相当于两桶总重量的，于是可以求出两桶水的总重量是：

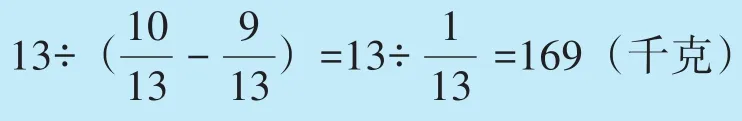
可见，只有抓住“总量不变”这个解题的突破口，才能使问题顺利得到解决。

《排队的类型》参考答案

300÷6=50（名）