基于MPSO-SVM 的不确定条形区域故障诊断研究

李默臣，姚 波，王福忠

（1.沈阳师范大学 数学与系统科学学院，辽宁 沈阳 110034；2.沈阳工程学院 基础教学部，辽宁 沈阳 110136）

容错控制概念自提出以来很快成为关注的焦点，并在航空、航天等技术领域得到广泛运用。根据容错控制的特点，将其分为被动容错与主动容错。被动容错［1-3］通过优先考虑执行器或传感器故障，一定程度上满足了系统的可靠性要求，但同时存在能耗高、保守性大等问题；主动容错通过故障预警，提前判断故障通道的位置，很好地解决了这类问题。支持向量机［4-6］（SVM）作为机器学习算法被广泛应用于统计学习理论及故障诊断领域。文献［7］针对SVM 中核宽度系数及惩罚因子难以获取的问题，采用网格搜寻法在条形区域下实现极点的精准分类，并设计闭环极点观测器来弥补极点信息难以采集的缺陷。文献［8］针对电梯故障特征难以提取、识别率差等问题，将电梯故障诊断信号源与时域指标相结合，构造故障特征向量，并应用最小二乘支持向量机（LSSVM）实现故障特征的有效分类。文献［9］针对粒子群算法中惯性权值取值唯一的问题，以DGEN380发动机故障为例，以燃油流量为输入，以低压转子的转速为输出，提出了应用改进的粒子群算法对发动机故障进行系统辨识。文献［10］针对BP神经网络在人脸识别中具有收敛速度慢的缺点，提出了应用MPSO改善BP神经网络的分类效果，更合理地确定连接权值和阈值。文献［11］依据PSO 全局寻优的高效性和混沌算法局部搜索的随机性，给出混沌粒子群混合算法，通过几种函数的测试，证明该方法对数据分类是有效的。

本文主要研究在不确定条形区域下，执行器发生连续增益故障，可靠控制器的设计问题。为解决闭环极点难以获取的问题，设计全维状态观测器以实现极点的在线采集；同时，针对SVM 参数选取易受主观先验知识影响及PSO 算法易陷入局部极值的缺陷，提出了一种使惯性权值自适应调整策略更加完善的MPSO-SVM 算法。与网格搜寻法（Grid search-SVM）和粒子群算法（PSO）相比，该算法的分类准确率能够达到98.888 9%，证明了其有效性和可行性。

1 MPSO-SVM 理论核心

1.1 SVM理论

SVM 作为智能学习算法之一，在小样本分类及非线性问题上应用较多。其基本思想是以获得最优分类超平面为目标，以构造映射ς:R→H为主要方式，从而获得问题的最优解。现存在样本集为

在SVM 理论中，核参数对系统的识别能力影响较大，不同值会产生不同的泛化效果。同时，错分样本的惩罚程度由惩罚因子决定，其大小也关乎系统的分类精度。因此，优化参数对SVM 的分类效果至关重要。相比于网格搜寻法与遗传算法，粒子群优化算法具有调整参数少、收敛速度快等优点，更适合应用于极点配置与分类问题当中。

1.2 PSO理论及改进

PSO 算法可看成无质量且无体积的粒子在只有速度和位置的约束下，在解空间不断更新并寻求最优解的过程。其中，个体极值被称为每个粒子寻觅的最佳位置，群体极值被称为整个群体寻觅的最佳位置。PSO的基本思想如下：

式中，wmax为惯性权值上限；wmin为惯性权值下限；tmax为迭代次数上限；t为当前迭代次数。为解决w前期较大，影响初期PSO 算法局部搜索性的问题，应加速w的前期递减速度，避免引起早熟；减慢w后期的递减速度，确保局部寻优过程中逐渐收敛。其公式为

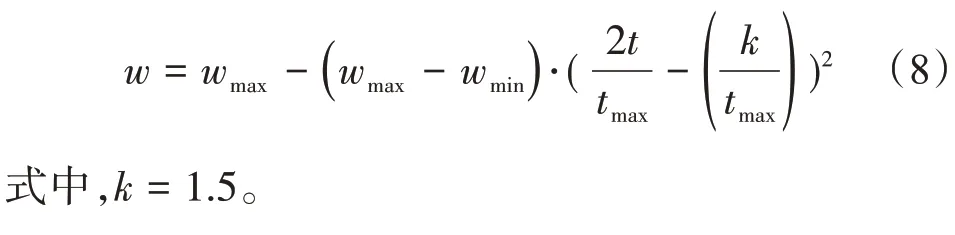
2 极点观测器的设计

针对闭环系统极点数据采集困难的问题，该设计依据系统状态估计极点的方式，即极点观测器。假设系统为

式中，x(t)为时变矩阵，x(t)∈Rn。在假设状态可测情况下，根据系统状态估算矩阵A，若初始时间为t1，采样间隔为Δt，预采集n个状态值，具体算法如下：

3 MPSO-SVM 理论模型

与传统网格搜索法相比，本文应用MPSO 算法优化SVM 中的核宽度系数g和惩罚系数c来实现极点分类。该方法具有运行时间短，分类效果显著等优势。具体过程如下：

步骤1：对故障通道的极点数据实时采集，形成样本数集。

步骤2：对PSO 算法中的参量进行初始化处理，修改惯性权重公式。在此期间划分测试集与训练集，并完成数据预处理工作。

步骤3：任取两个粒子，一个代表核宽度系数g，另一个代表惩罚系数c，存入模型。

步骤4：运行程序并根据第i个粒子的个体极值、群体极值及适应度值选择是否更新速度和位置。

步骤5：若适应度值较差，则返回步骤2；否则，迭代终止，输出结果。

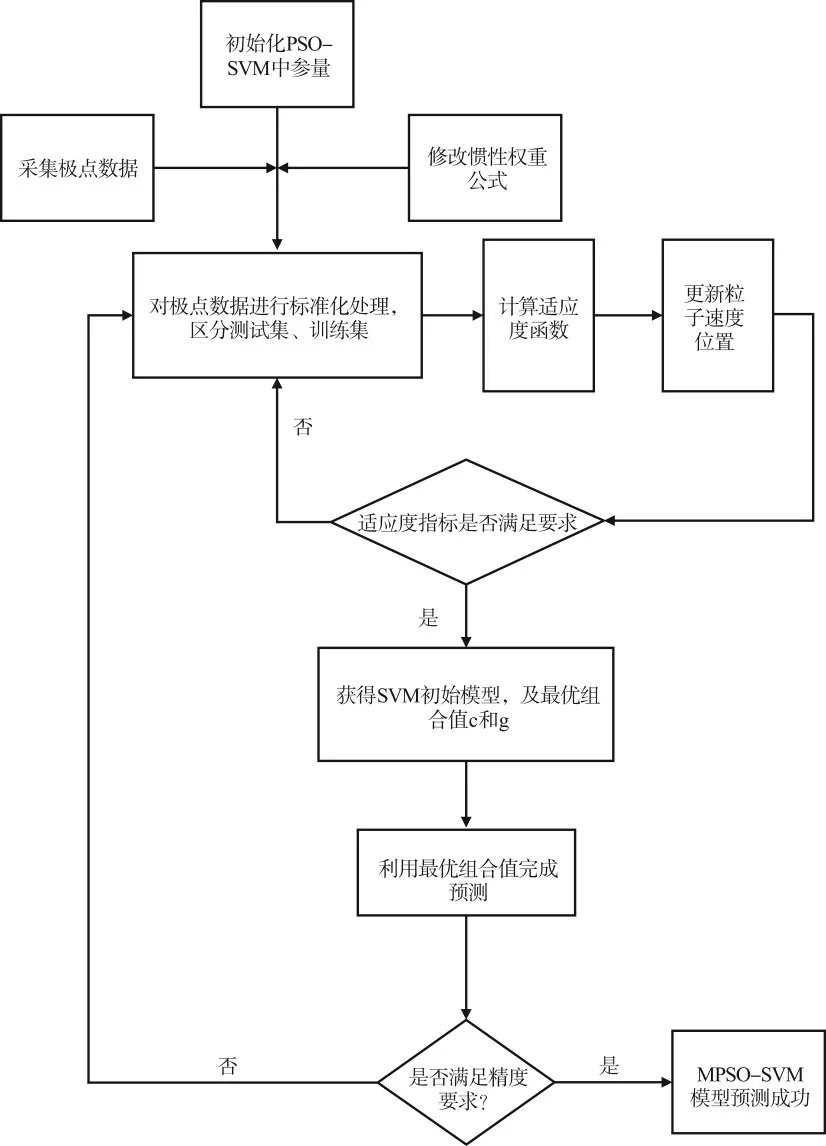
图1 MPSO-SVM 预测模型流程

4 改进粒子群算法在不确定条形区域的应用

4.1 问题描述

对于以下系统：

式中，ΔZ=DH(t)E，D和E为适维矩阵，且是定常的。H(t)为可测Lebegueke，且有HT(t)=H(t)≤I。而x(t)∈Rn、y(t)∈Rp和u(t)∈Rq分别为系统的状态变量、输出及控制变量，矩阵A、B和C满足不确定系统成立的充分必要条件。

引入静态输出控制器u(t)=Ky(t)，此时闭环系统为

4.2 引理、定理

引理1若保证A的所有特征根均被约束在h1及h2的垂直条形区域内，当且仅当存在正定矩阵P，满足

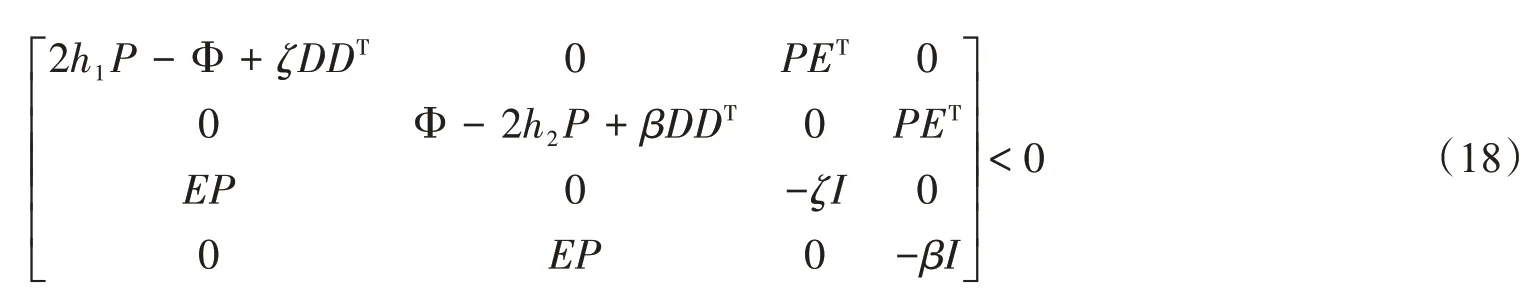
引理2X和Y为常数矩阵，H为时变矩阵，且都满足相应维数要求，若HTH≤I成立，那么对任意常数ζ＞0有XHY+YTHTXT≤ζXXT+ζ-1YTY。

1）Σ ＜0；

2）Σ11＜0,Σ22-Σ21Σ11

-1Σ12＜0；

3）Σ22＜0,Σ11-Σ12Σ22

-1Σ21＜0。

定理1对于上述系统（15），若保证极点均满足h1到h2的垂直条形区域约束要求，当且仅当存在常值ζ＞0、β＞0、对阵矩阵P和矩阵V、U、K，满足

式中，Φ=AP+PAT+BUC+CTUTBT，则有K =UV-1使得特征极点满足条形约束条件。

证明：根据引理1可有下列矩阵不等式成立：

在利用引理3，可得定理。

定理2 对于系统（16），当发生执行器故障uf(t)=F au(t)时，若保证极点均满足h1到h2的垂直条形区域约束要求，当且仅当存在常值ζ＞0、β＞0、对阵矩阵P和矩阵V、U、K，满足

式中，Γ=AP+PAT+BFaUC+(BFaUC)T,且Ki=UV-1(i=1,2,…,n)。

证明：从略。

5 仿真研究

考虑如下系统：

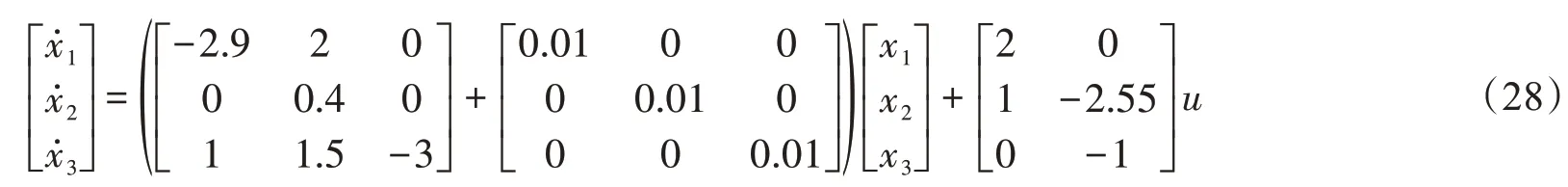
H为单位矩阵，若使闭环系统极点a+bi 稳定在h1=-4.5，h2=-1.5 的条形区域，则存在静态反馈控制器为

此时，极点均稳定在条形区域内。

5.1 不同算法可视化分析

若执行器发生连续增益故障Fa=diag(f1,f2)，则极点跳出条形区域，此时系统不能正常运行。第一条通道故障情况如图2所示，f2=1,0.3 ＜f1＜1.4；第二条通道故障情况如图3所示，f1=1,0.5 ＜f2＜1.8。

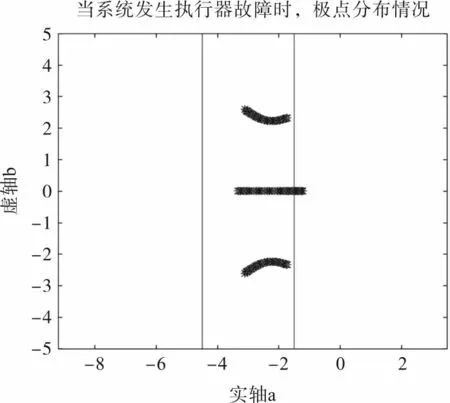
图2 第一条通道故障极点分布

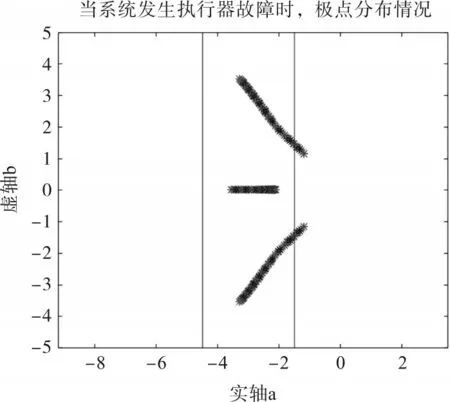
图3 第二条通道故障极点分布

分别采用Grid search-SVM 及PSO-SVM 对SVM 中的参数进行调整优化，如图4 和图5 所示。当c=512、g=64时，得出的最佳精准率为81.25%；当种群数量为30，学习率分别为c1=1.6 和c2=1.5时，最佳适应度曲线逐渐稳定，趋近于79.166 7%，此时的参数组合值为c=13.009 7、g=2.977 6。由此可判断，这两种算法并不能满足系统的分类要求，详细信息如表1所示。

表1 不同模型结果表

现采用MPSO-SVM 算法，效果如图6 所示。当c=58.854 7、g=12.238 7 时，时间消耗为5.156 3 s，分类准确率高达98.888 9%。

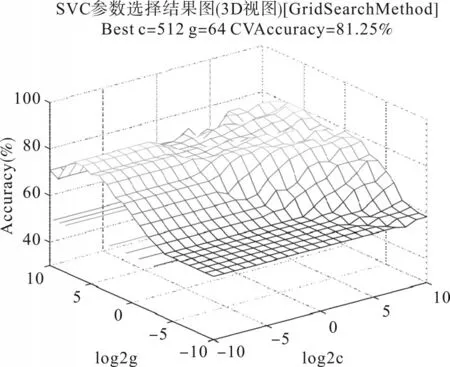
图4 Grid search-SVM 参数选择3D视图

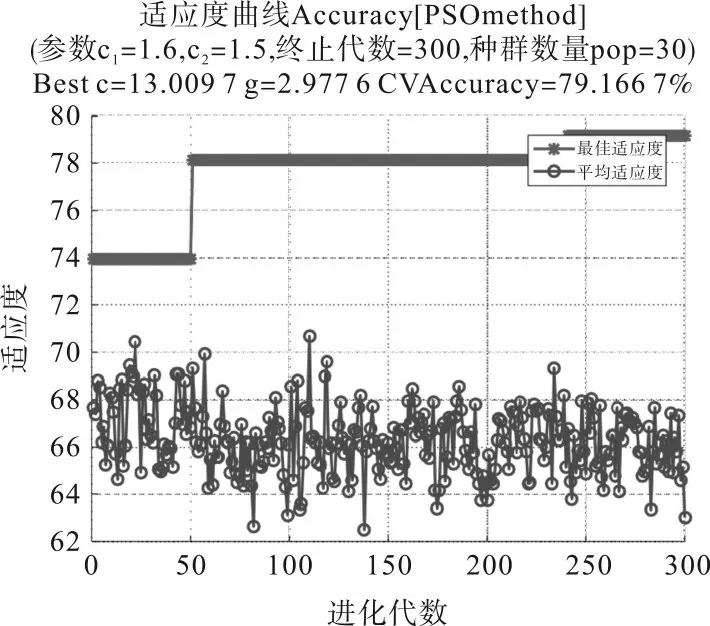
图5 PSO-SVM 适应度曲线

图6 MPSO-SVM 适应度曲线

通过以上3种算法对比可知，MPSO-SVM 算法在不确定条形区域极点配置问题中效果显著。

5.2 极点观测器测试

现对执行器发生故障情况进行模拟，以实现对闭环极点观测器有效性的验证。设系统第一条通道出现故障F=diag()f1,f2，即f1=0.34、f2=1。此时，有1 个极点跳出条形区域，极点集为λ={-3.068+2.569i,-3.068 -2.569i,-1.25}，而根据极点观测器求得极点集 λ^={-3.128+2.439i,-3.114 -2.442i,-1.23}，对 比 可得计算值无限逼近真实值。通过取时间间隔t1=0.1、t2=0.11、t3=0.12 和t4=0.13，并设初始值x(0)=[1,1,1]T，根据公式x(t)=eAtx(0)可得

x1=[0.111 8,0.764 3,0.960 2]T、x2=[0.044 0,0.743 2,0.950 0]T、x3=[-0.020 3,0.722 5,0.939 0]T、x4=[-0.0813,0.7023,0.9272]T、ΔX=[x2-x1,x3-x2,x4-x3]、X=[x1,x2,x3]Δt。

而X可逆，即可求公式（13）中的矩阵A。设系统发生故障时间t=0 s、Δt=0.01 s，误差公式为

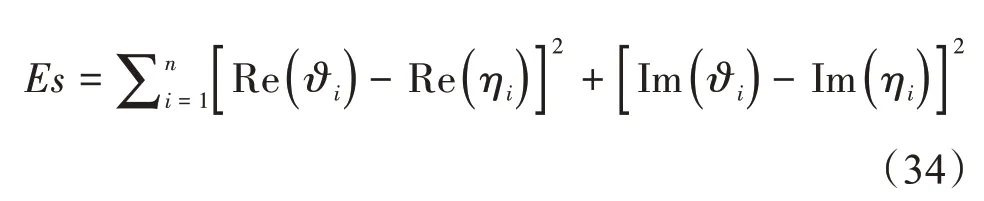
式中，Re()为极点的实部；Im()为极点的虚部。计算可得Es=0.057 3，直接证明了极点观测器是可靠的。

5.3 MPSO-SVM 故障诊断器测试

依据MPSO-SVM 建立模型并完成可靠控制器的设计，能够得到系统期望的性能，当极点稳定在条形区域时，系统仍在原控制器下保持正常运行；若极点逃逸，立即调换设计好的控制器，保持系统稳定运行，如图7和图8所示。

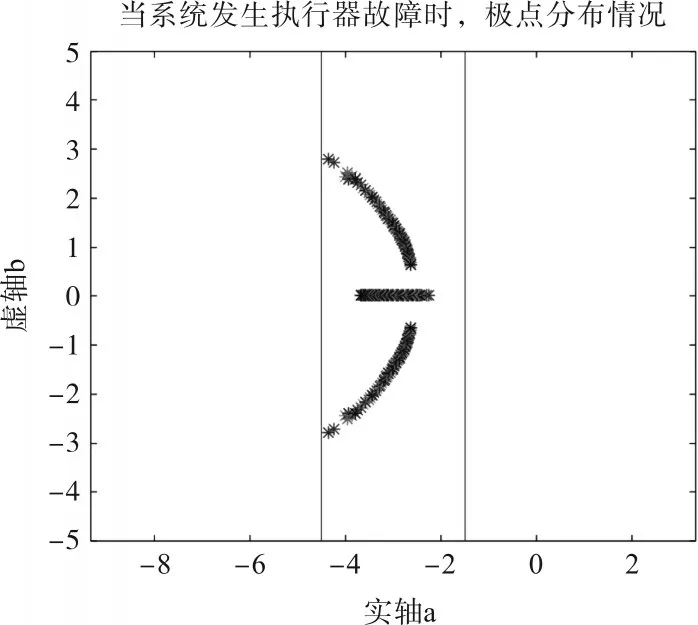
图7 针对第一条通道故障极点配置

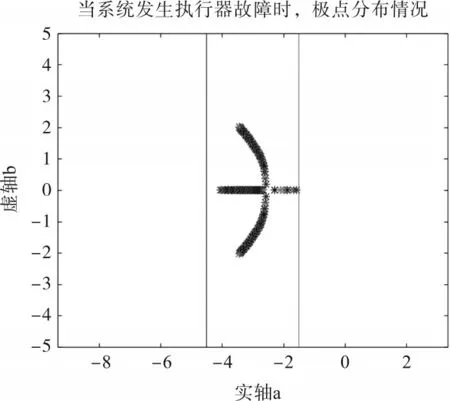
图8 针对第二条通道故障极点配置

6 结论

粒子群算法对区域极点配置效果明显，本文基于MPSO 算法的特点，通过完善惯性权重公式，有效地解决算法实现过程中全局搜索与局部搜索容易失衡的缺陷，将该方法用于SVM 参数寻优，准确率得到明显改善；针对极点信息难以获取的问题，设计了极点观测器，实现了闭环极点信息在线采集。同时，依据算例仿真，并结合多个算法进行对比，可得该方法设计的控制器鲁棒性能明显，在执行器出现故障，但极点仍处在条形区域时，系统不会做出响应；一旦极点逃逸条形区域，立即调换相应的可靠控制器保持系统正常运行。