钢纤维活性粉末混凝土三点弯曲试验数值模拟

王晓飞 张晓虎 周海龙

(1.内蒙古农业大学水利与土木建筑工程学院，内蒙古 呼和浩特 010018； 2.贵州工程技术应用学院土木建筑工程学院，贵州 毕节 551700)

1 概述

活性粉末混凝土(Reactive Powder Concrete)是一种新型超高强度、高耐久性及体积安定性良好的水泥基复合材料[1-3]。素RPC性脆，为提高其延性与韧性常掺入钢纤维。由于其优越的物理力学性能及耐久性，在铁路[4]、桥梁[5]、市政工程及军事防护等领域得到了迅速发展和应用[6]。

目前为止，国内外相关学者对RPC力学性能进行了较全面的研究，包括RPC单轴压缩[7-10]、三轴压缩[11]、弯拉性能[12]、单轴拉伸[13]、疲劳试验[14,15]及动荷载作用下的力学性能试验研究[16,17]，试验成果较多也较全面。与力学性能试验成果相比，钢纤维RPC在外荷载作用下的数值模拟研究成果较少，数值模拟方法能够从机理上探索和解释钢纤维RPC的破坏过程和破坏特征，并可开展相对复杂受力状态下的破坏过程和结果分析。本文对钢纤维体积含量为1% RPC棱柱体试件在三点弯曲试验条件下的力学行为进行了数值模拟，发现数值模拟结果与试验结果较吻合，说明了该数值模拟方法的合理性与可行性，以期对后续钢纤维活性粉末混凝土在复杂应力作用下力学行为数值模拟的实现以及在探索和理解钢纤维与RPC基质间的摩擦滑移作用机理有所帮助。

2 数值模拟

2.1 数值建模

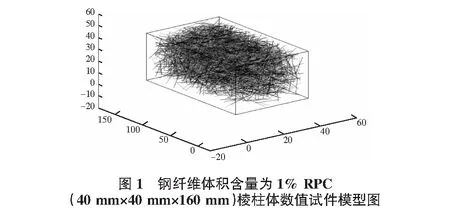
由文献[18]所提的钢纤维外包六面体法，完成棱柱体试件的数值建模过程，所建模型如图1所示。

2.2 网格划分及优化

2.2.1初始网格划分

钢纤维体积含量为1% RPC棱柱体试件(40 mm×40 mm×160 mm)数值建模完成后，钢纤维端点坐标值被自动记录并储存，利用ansys软件对棱柱体数值模型进行正六面体分网，六面体网格边长设定为2 mm，把分网后形成的六面体单元节点坐标值提取出来，这样，在数值模型域内形成一个由钢纤维端点和正六面体单元节点组成的点云群。由Matlab软件编程对点云群中的点进行四面体网格划分得到钢纤维体积含量为1% RPC棱柱体数值模型的初始四面体网格划分。

2.2.2网格质量优化

由于钢纤维端点在试件域内分布的随机性，初始四面体网格质量一般较差，可能会导致在数值模拟计算过程中出现沙漏现象而无法获得理想的数值模拟结果，因此对四面体网格优化是必要的。

对于整个数值试件来说，如果每个四面体单元的各边都相等，这种情况下网格质量是最理想的。本文在对棱柱体初始四面体网格优化过程中，钢纤维端点不动，正六面体单元节点(包括数值试件表面及内部节点)每优化循环计算一次，位置变动一次，网格总体质量优于上一次。网格优化依据桁架力学原理并由Matlab软件编程实现。现以平面网格优化问题解释说明空间四面体网格优化的具体思路和方法。

如图2所示A点为数值模型内部或表面上节点(非钢纤维端点)，在网格优化过程中可动，与其连接的每一条边均为三角形单元边长。假设每条边对节点的作用力F计算公式为：

F=l0-l

(1)

其中，F为三角形单元边对所连接节点的作用力；l0为在总节点数一定的情况下，假设数值模型中所有三角形单元各边均相等时的边长；l为与节点相连三角形单元边长。

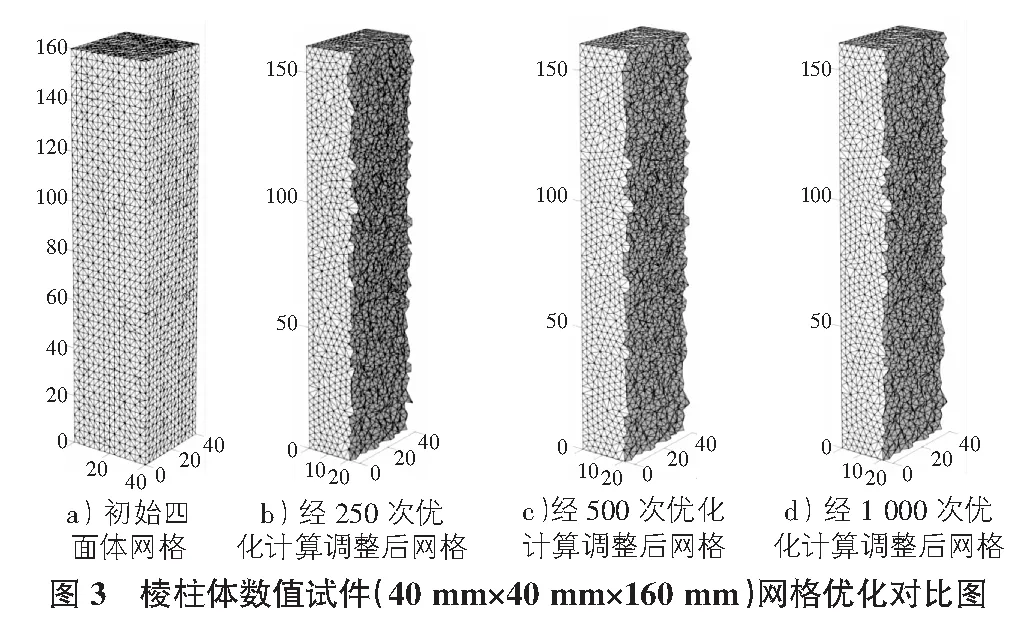
假设边长对节点的作用力压为正，拉为负。当边长l>l0时，边对节点的作用力为拉力，背离节点。当边长l

节点位置每次调整后，需要判断节点新位置是否仍在数值试件域内，如果节点在位置优化循环调整过程中跳出试件域，则不储存跳出点的坐标信息，该点从点云中剔除，不再参与网格优化调整过程。图3为棱柱体试件初始网格划分图及经过一定次数优化循环调整后网格质量对比图，为体现数值试件内部网格调整变化情况，取一半棱柱体试件比较分析。

由图2和图3可知，经一定次数循环优化计算调整后的网格质量明显优于初始四面体网格，循环调整次数越多，网格质量越好。为后续数值模拟计算过程的顺利进行及数值模拟计算精度的提高奠定了坚实基础。

经1 000次循环优化调整后，得到最终的四面体网格。钢纤维选为杆单元，每根钢纤维为一个杆单元，RPC混凝土基质选用Solid164单元，钢纤维体积含量为1% RPC棱柱体(40 mm×40 mm×160 mm)数值试件经优化后的四面体网格，共有杆单元5 183个，Solid164单元156 699个，钢纤维与RPC基质间的摩擦握裹力由杆单元节点力体现。

棱柱体数值试件加载过程设置与实际试验加载过程完全相同。在数值试件上表面中部设置直径为10 mm的钢筋作为荷载施加端，而在数值试件下表面对应位置设置两根直径为10 mm的钢筋作为支座，加载方式位移控制，加载速率为0.002 mm/s。钢纤维体积含量为1% 棱柱体(40 mm×40 mm×160 mm)数值试件弯拉试验加载过程如图4所示。

2.3 本构关系及破坏准则

2.3.1本构关系

由各向同性线弹性本构模型描述钢纤维杆单元与RPC基质单元应力—应变关系，加载时试件上下表面钢筋同样也服从各向同性线弹性本构模型。

2.3.2破坏准则

本文材料的破坏选用最大拉应力破坏准则，认为材料的破坏是由于危险点上的最大主拉应力超过了材料的许用拉应力导致的。

σ1≤[σ]

(2)

其中,[σ]为材料的许用拉应力。

2.4 材料力学性质参数

数值模拟计算过程中，钢纤维RPC数值试件中各相材料力学性质取值，见表1。钢纤维材料力学参数由生产厂家提供，RPC基质材料力学参数由试验确定，加载时棱柱体上下表面3根直径为10 mm圆钢的材料力学性能取低碳钢相关的力学性能参数。

表1 钢纤维RPC数值模型各相材料力学参数表

2.5 棱柱体内代表性点水平向正应力时程曲线

图5～图8为数值试件在加载过程中棱柱体上四个代表性位置RPC基质单元水平方向正应力时程变化曲线(拉应力为正，压应力为负)。

图5b)曲线为图5a)所示棱柱体弯梁跨中截面底部A点所在位置RPC基质单元水平向正应力加载时程变化曲线。由图5b)可知，图5a)中所示A点基质单元水平正应力随加载的持续，在破坏前几乎成线性增加，且为拉应力，当加载时间约1 700 s时，试件突然开裂，试件开裂后A点位置四面体单元正应力突然降到0点附近，随裂缝的不断发展，该点正应力在0点附近较小范围内波动。

由图5b)所示数值模拟得到的棱柱体抗折强度为23.50 MPa,而实测试件的抗折强度为22.19 MPa,数值模拟所得强度与实测抗折强度很接近，且破坏前线性变化趋势与材料力学相关结论一致，说明本文所提数值模拟方法切实可行。

图6b)曲线为图6a)所示棱柱体跨中截面顶部A点RPC基质单元水平向正应力随加载时间变化曲线。由图6b)可知，图6a)中所示A点正应力随加载时间的增加，在破坏前近似线性增加，且为压应力。当加载时间约1 700 s时，试件开裂，开裂瞬间A点正应力突然降低到一个较小的应力水平。在加载过程中A点位置RPC基质单元破坏时水平向最大正应力约为26.5 MPa,与跨中截面底部基质单元最大拉应力接近，这也与材料力学相关理论分析结果一致。

图7b)曲线为图7a)所示棱柱体跨中截面中性层A点基质单元水平向正应力加载时程变化曲线。由图7b)可知，图7a)中所示A点正应力随加载时间的增加，在破坏前随加载时间几乎在做正弦波波动，波动幅度很小，可认为在破坏前该位置基质单元水平正应力很小或无正应力。数值试件开裂瞬间该单元突然产生一个瞬间的拉应力，马上降低并在0点附近波动最终趋于0，这也与材料相关力学理论分析结果一致。

图8b)曲线为图8a)所示棱柱体两支座外A点对应的基质单元水平向正应力加载时程变化曲线。由图8b)可知，图8a)中所示A点正应力在破坏前，随加载时间的增加几乎不产生水平向正应力，数值试件逐渐开裂过程中，该单元体产生较小幅度的水平正应力波动，这也与材料力学理论分析结果一致。

2.6 破坏模式比较

如图9a)所示为钢纤维体积含量为1% 40 mm×40 mm×160 mm实体棱柱体试件三点弯曲试验破坏模式图，如图 9b)所示为对应数值试件破坏模式。比较两图可以清楚发现，数值模型与实体试件破坏模式是一致的。

3 结论

1)在棱柱体数值试件各项材料都选用线弹性本构模型及最大拉应力破坏准则前提下，实现了对棱柱体数值试件三点弯拉试验过程数值模拟。

2)通过对比数值模拟结果与试验结果可以发现，不论在破坏过程、弯拉强度和破坏模式上数值模拟效果都是较好的。

3)数值模拟结果说明了本文提出的四面体网格优化方法及数值模拟方法的可行性与有效性，为后续高掺量钢纤维活性粉末混凝土在复杂应力作用下的数值模拟的实现奠定一定基础，并为理解和探寻钢纤维与RPC基质间的摩擦作用机理有所帮助。

Numericalsimulationofthree-point