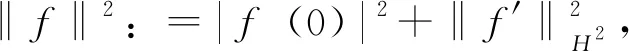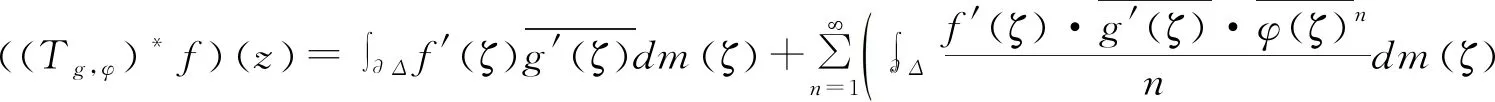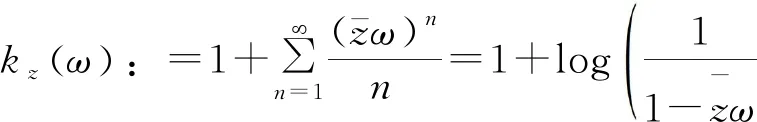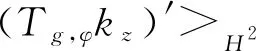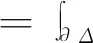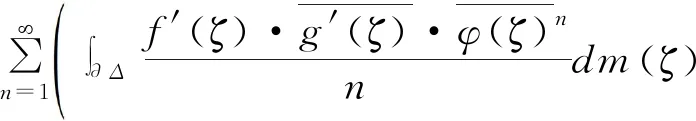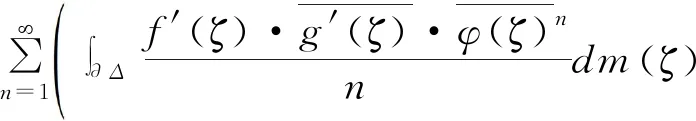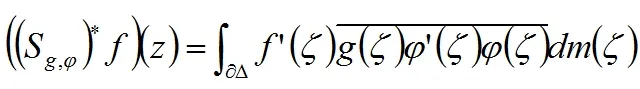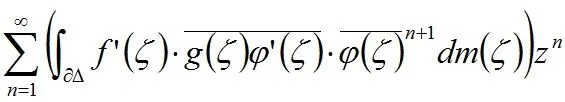广义Volterra型算子在导数Hardy空间上的有界性及紧性
罗庆仙
(广东茂名幼儿师范专科学校 理学院, 广东 茂名 525200)
0 引言
Volterra型算子在各种函数空间上的有界性和紧性等问题的研究一直是一个热门的研究课题。其中,数学家Pommerenke[1]首次刻画了Volterra型算子在Hardy-Hilbert空间H2上的有界性[1]。在他的工作基础上,Aleman、Siskakis和Cima[2-3]系统地研究了Volterra型算子在Hardy空间Hp(0 在本文里,我们将继续研究作用在导数Hardy空间上广义Volterra型算子。广义Volterra型算子由李颂孝和Stevic所引进并很快吸引了大量学者的研究兴趣[14-15]。最近,Mengestie[16-17]研究了广义Volterra型算子在加权Fock空间上的有界性和紧性。受文献[13,18]的启发,本文将利用加权复合算子在Hardy空间上的性质给出广义Volterra型算子在导数Hardy空间(即导数属于Hardy空间的解析函数所组成的函数空间)上的有界性和紧性的完整刻画,推广了文献[19]中的结果。最后刻画了该类算子的伴随算子的泰勒展开式。 首先,我们用H(Δ)表示复平面单位圆盘Δ上所有解析函数f组成的函数空间。对于0 其中m是单位圆盘Δ的边界∂Δ上的Lebesgue测度且m(∂Δ)=1。由文献[20]中的定理9.4可知,上面的范数定义与如下的范数是相等的: 其中对于任意的ξ∈∂Δ,f(ξ)是f在边界∂Δ上的径向极限(由Fatou引理,这是几乎处处存在的)。 当p=∞时,H∞是单位圆盘Δ上所有有界解析函数f组成的函数空间且定义它的范数为f在Δ上的上确界。 对于g∈H(Δ),Volterra型算子Tg及其伴侣算子Sg的定义分别如下: 其中,z∈Δ,f∈H(Δ)。 近年来,林庆泽等人研究了Volterra型算子在导数Hardy空间上的有界性[19]。对于0 当1≤p≤∞时,Sp是一个Banach代数且有嵌入关系:Sp⊂H∞。关于导数Hardy空间Sp的一些基本结构性质可参考文献[18-19,21-23]。本文的研究需要用到加权复合算子的相关性质。对于给定的φ∈H(Δ)以及Δ的解析自映射φ,加权复合算子Wφ,φ的定义如下: 对于导数Hardy空间上的算子的研究可追溯到Roan的关于复合算子在导数Hardy空间上的有界性的工作[22]。随后的相关工作可参考文献[29-32]。 这一节主要研究作用在导数Hardy空间上的广义Volterra型算子 的有界性和紧性。首先,我们先研究广义Volterra型算子Tg,φ:Sp→Sq的有界性和紧性。 定理1 令1≤p,q≤∞。则广义Volterra型算子Tg,φ:Sp→Sq是有界的当且仅当g∈Sq。 证明 对于f∈Sp,我们有恒等式 反过来,我们也有恒等式 通过上面的类似证明和文献[18]中的命题3.3,我们得到下面关于算子Tg,φ:Sp→Sq的紧性的充要条件: 定理2 令1≤p,q≤∞。假定广义Volterra型算子Tg,φ:Sp→Sq是有界的,则算子Tg,φ:Sp→Sq是紧的当且仅当 (a)如果(p,q)≠(1,∞),则g∈Sq; 下面,我们研究另一类广义Volterra型算子Sg,φ:Sp→Sq的有界性和紧性。 定理3 令1≤p,q≤∞。则广义Volterra型算子Sg,φ:Sp→Sq是有界的当且仅当 (c)如果1≤q≤p=∞,则gφ′∈Hq; (d)如果1≤q 证明 对于f∈Sp,我们有恒等式 反过来,对于f∈Hp,我们可以验证下面的恒等式成立: (Wgφ′,φf)(z)=f(φ(z))g(z)φ′(z) 因此,算子Sg,φ:Sp→Sq的有界性等价于加权复合算子Wgφ′,φ:Hp→Hq的有界性。从而由文献[25]中的定理4可得到定理中的条件(a),由文献[24]中的命题2.6可得到定理中的条件(b)和(c),再由文献[25]中的命题2可得到定理中的条件(d)。证毕。 通过上面的类似证明,我们得到下面关于算子Sg,φ:Sp→Sq的紧性的充要条件。 定理4 令1≤p,q≤∞。假定广义Volterra型算子Sg,φ:Sp→Sq是有界的,则广义Volterra型算子Sg,φ:Sp→Sq是紧的当且仅当 (c)如果1≤q 证明类似于定理3的计算,算子Sg,φ:Sp→Sq的紧性等价于加权复合算子Wgφ′,φ:Hp→Hq的紧性。从而由文献[25]中的定理5和文献[20]中的定理2.3可得到定理中的条件(a),由文献[24]中的命题3.2可得到定理中的条件(b),由文献[18]中的命题3.4和文献[25]中的定理6可得到定理中的条件(c),再由文献[33]中的推论4.3可得到定理中的条件(d)。证毕。 定理5 若广义Volterra型算子Tg,φ:S2→S2是有界的,则其伴随算子具有如下的级数展开式: 因此,对于任意的z∈Δ,我们得到 ((Tg,φ)*f)(z)=<(Tg,φ)*f,kz>S2 = 因此,我们得到: 其中z∈Δ。定理得证。 类似于定理5的证明,我们得到: 定理6 若广义Volterra型算子Sg,φ:S2→S2是有界的,则其伴随算子具有如下的级数展开式 其中z∈Δ。1 广义Volterra型算子在导数Hardy空间上的有界性和紧性
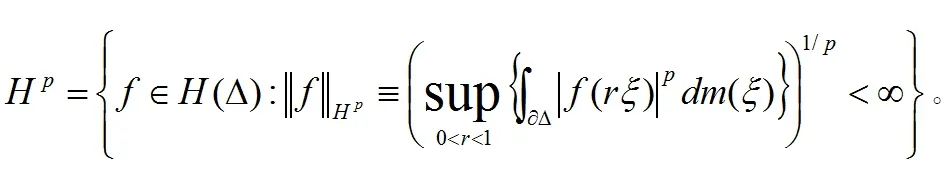
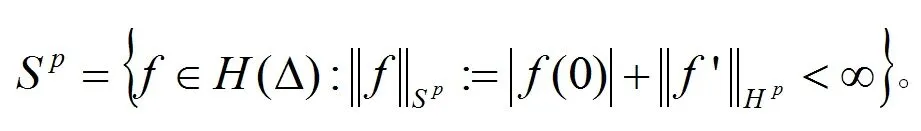



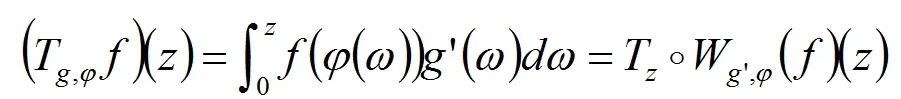

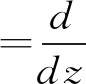
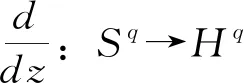
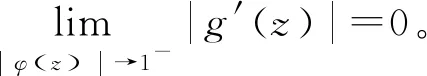
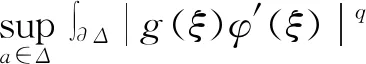
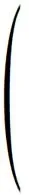

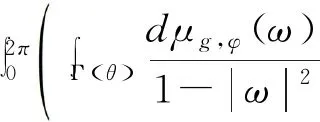

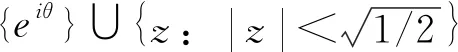
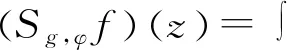
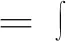

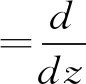
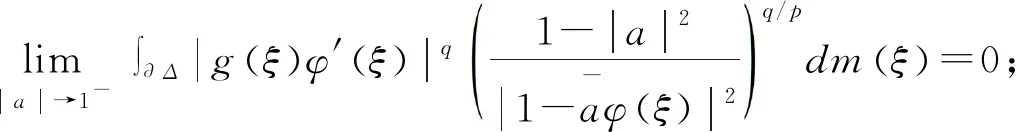
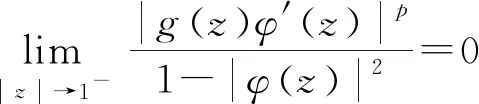
2 广义Volterra型算子在导数Hardy空间S2上的伴随算子