有理函数的迭代根

刘晓华，罗天琦

(1.乐山师范学院 数理学院，四川 乐山 614000；乐山师范学院 教师教育学院，四川 乐山 614000)

0 引言

映射的迭代和迭代根有着密切的联系，有时可以通过一映射的n次迭代找到它的n次迭代根。早在十九世纪数学家们就开始了对映射迭代根的研究[1-3]，但是直到二十世纪五六十年代才取得了突破性的进展[4-5]，其获得的结果主要是针对区间上单调连续自映射的。对于在区间上非单调的连续自映射其迭代根问题要难得多。文献[6]和[7]讨论了一类特殊的非单调连续自映射，就是只有有限个非单调点的连续自映射，称为严格逐段单调自映射，简称为PM-映射。对这类映射迭代根的研究，目前也取得了较大进展[8-14]。对于在区间上非单调不连续自映射的迭代根问题，到现在为此，研究甚少[15-16]。

在文献[17]中，我们研究了有理函数

(1)

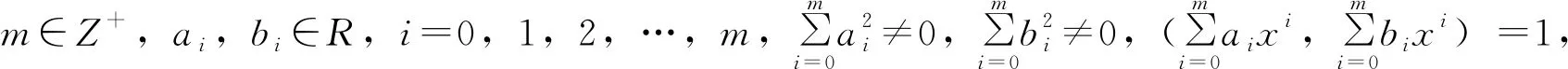
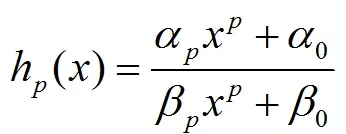
(2)

(3)

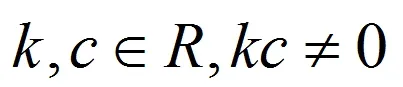
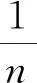
注：这篇文章中研究的函数都假定是有定义的，并且假定下文函数的迭代，也就是函数的复合都能进行。

1 有理函数的迭代根

在给定理之前我们首先给出下面要使用的由(3)定义的单项式的n次迭代公式

(4)

由归纳法，我们很容易得到上述公式。

定理假定hp(x)和Mk(x)分别由(2)和(3)定义。由(1)定义的有理函数Fm(x)的系数满足

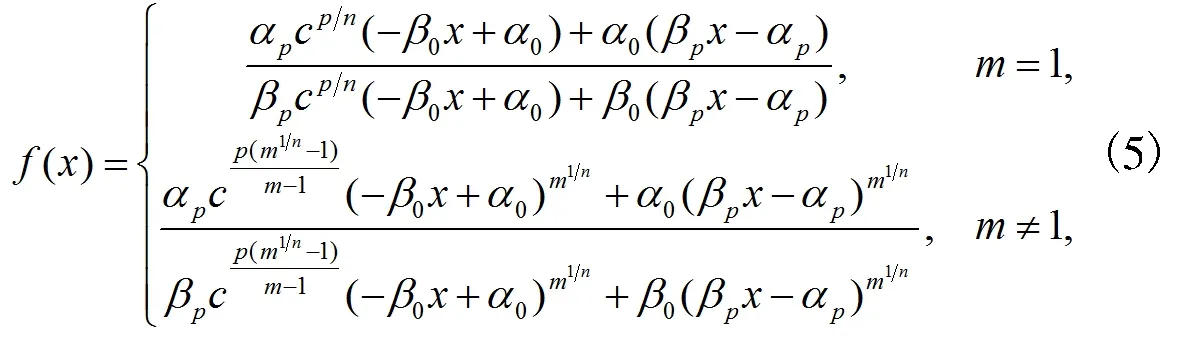
其中，n是一个使f(x)有意义正整数，或者有n次迭代根

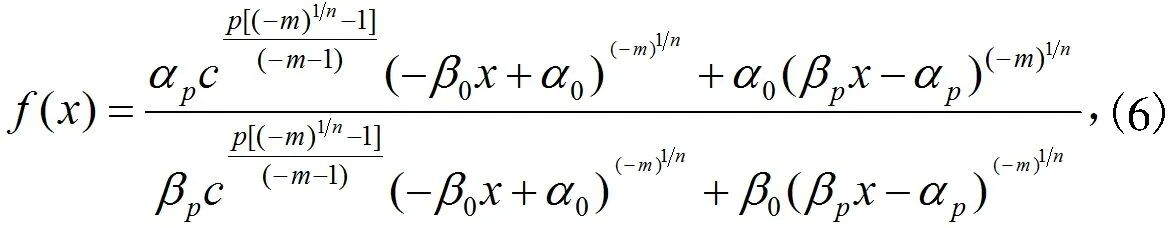
其中，n是一个使f(x)有意义正奇数。

证明 如果Fm(x)的系数满足

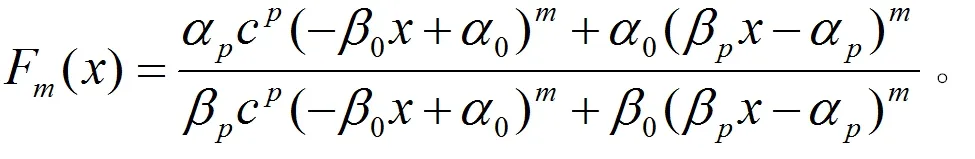
(7)

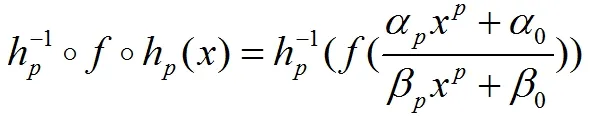
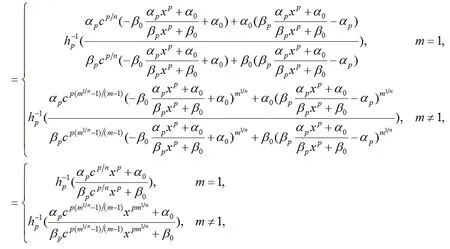
(8)

由公式(4)我们得到g(x)的n次迭代为

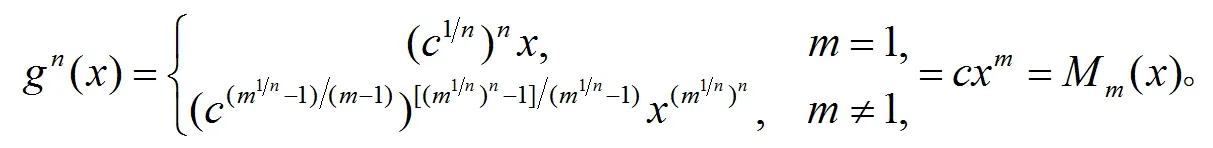
由(8)我们有

由(7)我们得到fn(x)=Fm(x)。因此，Fm有由(5)定义的n次迭代根f。

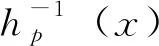
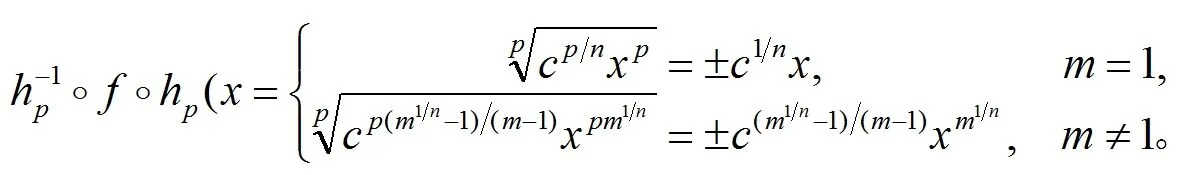
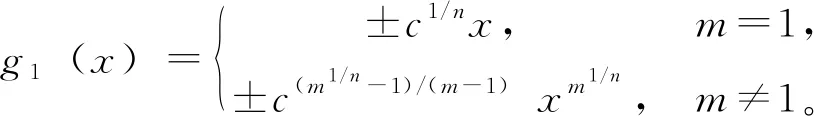
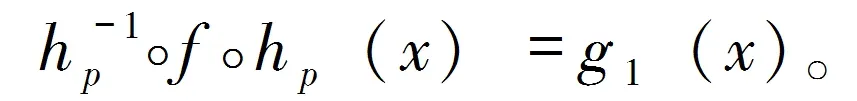
(9)

由公式(4)我们得到g1(x)的n次迭代为

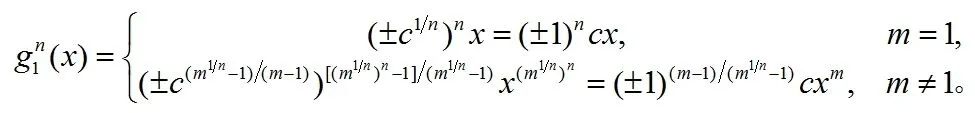
由(9)我们得到

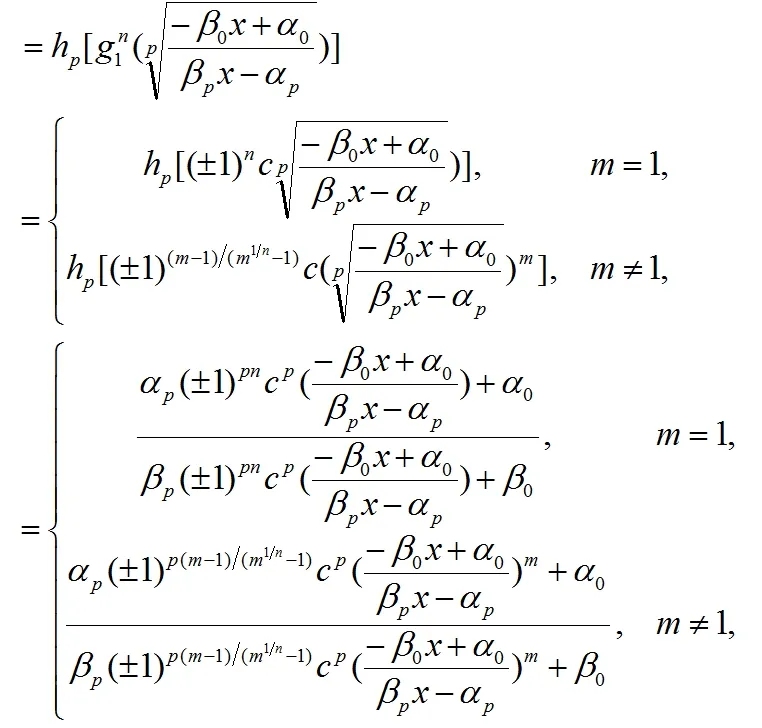
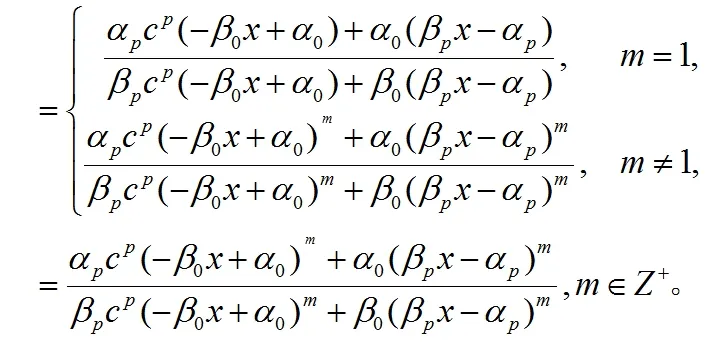
其次，我们证明(1)定义的有理函数Fm(x)的系数满足

和

时，其中i=0,1,2,…,m。在(2)定义的桥函数hp(x)下，Fm(x)有由(6)定义的n次迭代根f。注意，n是一个正奇数。根据Fm(x)的系数满足的条件，将其代入(1)我们得到

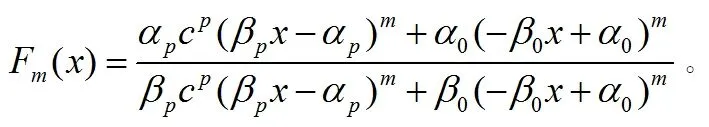
(10)

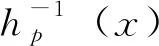
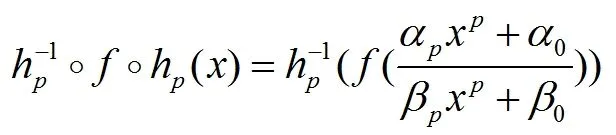
令g2(x)=c[(-m)1/n-1]/(-m-1)x(-m)1/n， 于是我们有

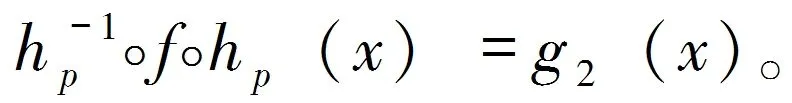
(11)

由公式(4)我们得到g2(x)的n次迭代为

由(11)我们有

由(10)我们得到fn(x)=Fm(x)。因此，Fm有由(6)定义的n次迭代根f。

当p是一个偶数时，假定f由(6)定义，我们用一个与上面类似的讨论，就能得到

(12)

由公式(4)我们得到g3(x)的n次迭代为

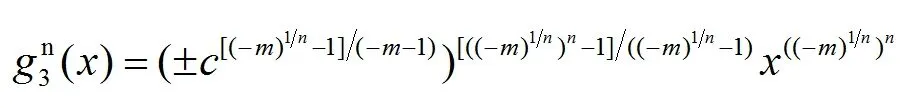
由(12)我们有

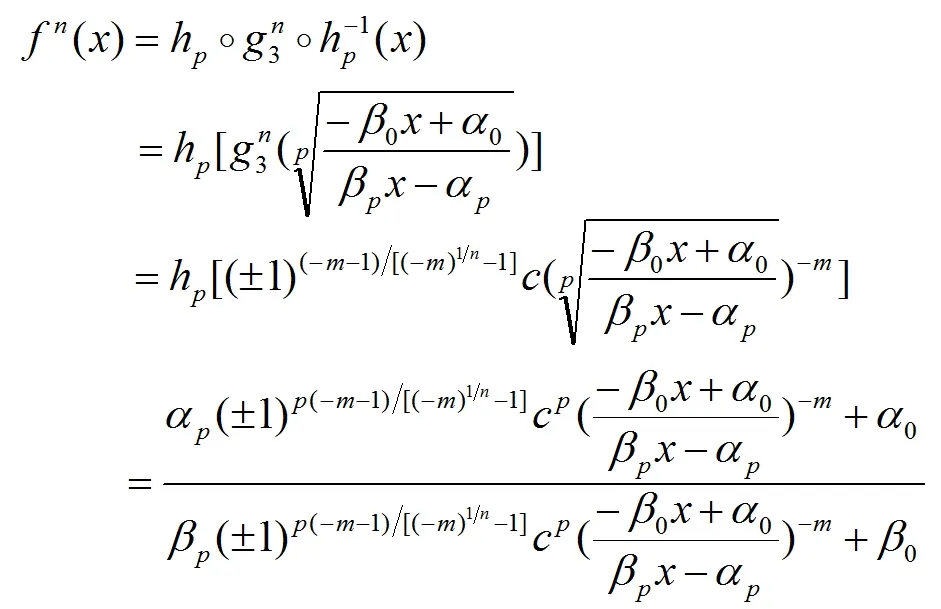
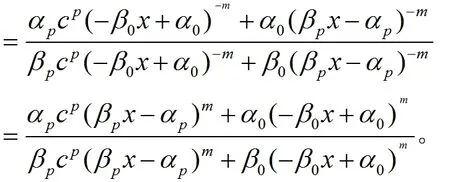
由(10)我们有fn(x)=Fm(x)。因此，Fm也有由(6)定义的n次迭代根f。注意，n是一个使f有意义的正奇数。否则，f没有定义。因此，这完成了定理的证明。

2 定理的应用

下面我们通过一些例子来展示定理的应用。

，

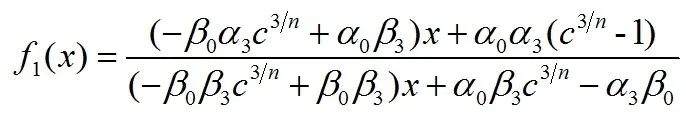
其中，n是使f1有意义的一个正整数。