油气行业补充医疗保险精算模型的构建
俞 强 兰正福 杨 枢 廖丹凤
(中国石油西南油气田分公司社会保险中心,四川 成都 610051)
0 引言
油气企业为担负经济责任和社会责任需要推进一系列改革,包括福利的合理配置。其中,企业补充医疗保险是最值得关注的问题之一[1-2]。虽然企业补充医疗保险有助于提高职工医疗保障水平,夯实人力资源基础,促进企业发展,但是对油气企业来说,需要随时关注国内外政治经济形势变化,扩大或缩小开支,以保证正常生产经营,这也使其对补充医疗保险的投入具有不确定性[3]。同时,人口结构、疾病谱的变化以及不断进步的医疗科学技术也使保障政策的制定充满复杂性。油气企业要建立补充医疗保险,就需要在职工保障水平和企业生产经营之间取得平衡,保证政策的稳健可持续[4-6]。
A 公司于2019 年开始医疗保障制度改革,组织人员调查收集了2011到2018年期间油田职工医疗费用数据,为油田医疗保障制度完善、成熟提供客观依据。笔者以A公司2011-2018年数据为依据进行模型构建。通过利用医疗保险精算学的基本原理对职工补充医疗保险进行分病种、性别和就职状态精算模型的构建,研究补充医疗保险资金运行情况,为油气企业建立企业补充医疗保险提供有价值的参考意见。
1 精算模型构建
所构建的企业补充医疗保险精算模型将资金的支出分为在职与退休两组,并分性别进行核算,增加了病种的划分,使该模型更接近事实,也更加精确[7-10]。按病种核算的职工补充医疗保险资金支出模型如公式(1)-(7)所示。
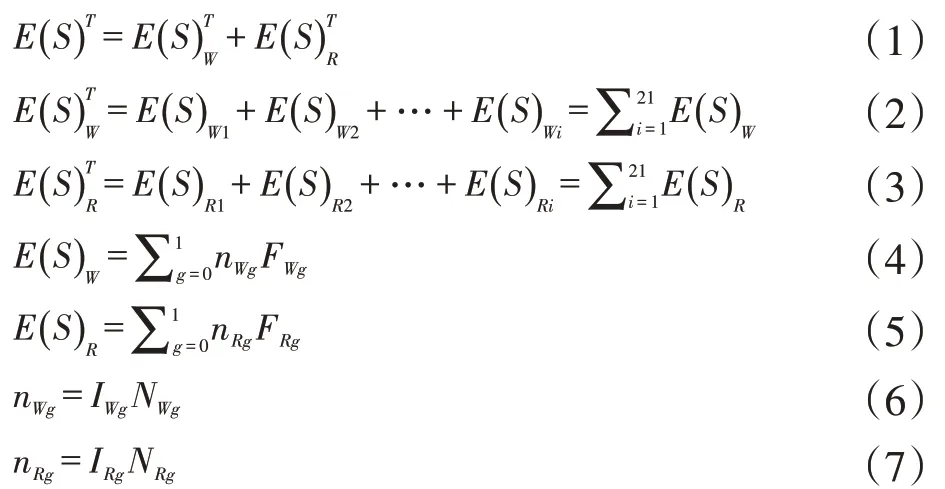
式中,E(S)T为T年资金支出总费用;为T年在职员工资金支出总费用;为T年退休员工资金支出总费用;下标W为在职,下标R为退休;i为疾病种类(国际疾病分类规定21 类);g为性别(g=0为女性,g=1为男性);I为发病率;n为某病的发病次数;N为参保人数;F为某病实际次均赔付额。
2 参数测算方法
依据上述模型公式,可以看出只需计算出发病率I、实际次均赔付额F、参保人数N,就可完成模型预测。
2.1 单病种发病率测算
单病种发病率测算以A 油气公司提供的2011-2018 年实际数据为基础,测算历年各病种的实际发病率。
从2011-2018年各病种的实际发病率发现,各病种各组的发病率均较为稳定,无明显趋势变化。因此,以2011-2018年各病种发病率的算术平均数做为精算模型中的发病率参数。
2.2 单病种次均赔付额测算
从2011-2018年实际数据来看,各病种次均医疗费用以及次均赔付额并不呈趋势性变化,也不呈周期性规律。且受变量限制,无法做广泛的联合分析。因此,本研究采用GM(1,1)灰度模型对该参数进行预测[11]。
GM(1,1)灰度模型预测的主要步骤如下:
利用原始数据,生成数据列。本研究采用2011~2018 年八年间某一病种的次均赔付额作为原始数据列x(0),一次累加后生成数据列其中:
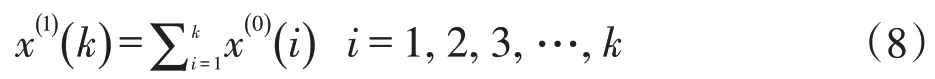
利用最小二乘法,求出参数a和u。首先利用x(1)求出其紧邻均值。令得到:
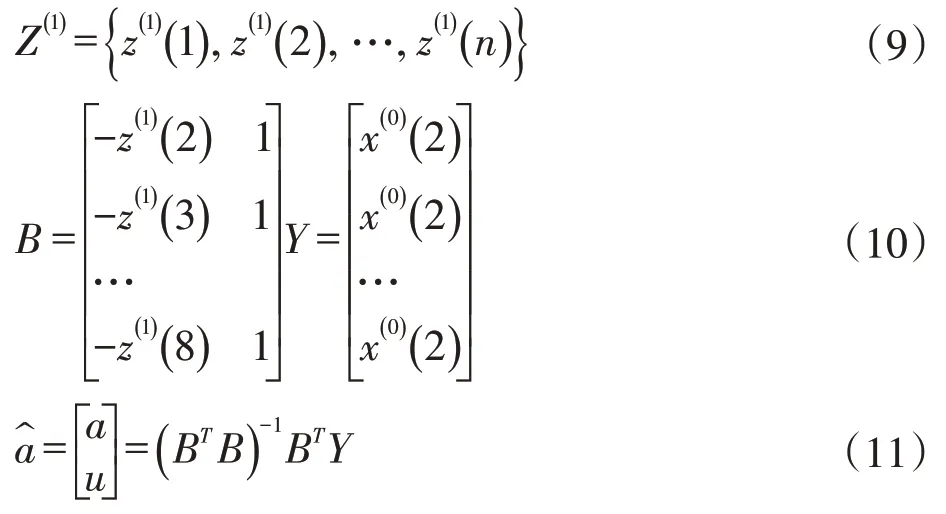
可计算得出a、u。
通过微分方程
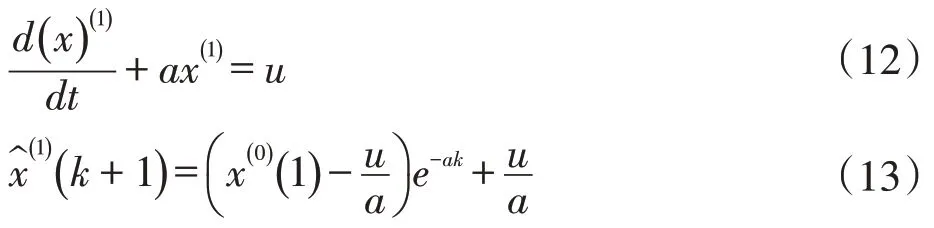
由公式(13)可计算得出x(1)的模拟值,则
还原x(0)的模拟值。
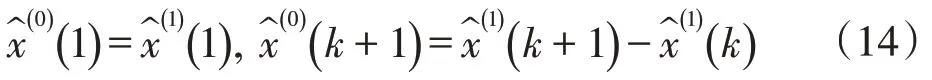
对预测结果进行精确度检验,精确度标准如表1所示。采用不同参数进行检验的结果可能不一致,较为常见的方式是通过相对误差对预测结果进行检验。
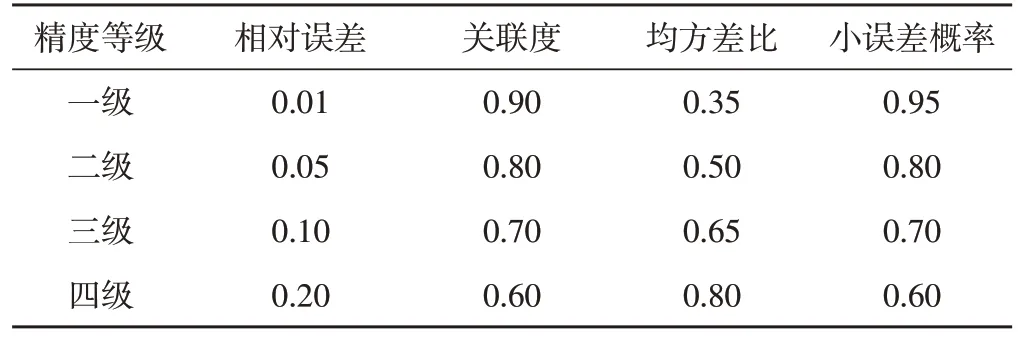
表1 GM(1,1)预测精确等级表
6)结果预测。若模型检验合格,可运用该模型进行预测。

2.3 参保人数测算
2011-2018年实际参保人数及每年的人数变化量如表2 所示。2011-2018 年各组参保人数变化存在明显的趋势性,在职员工总体上呈现逐年减少的趋势,而退休员工数量则在逐年增加。
由于各组参保人数呈现明显的趋势性变化,因此本研究采用趋势外推法预测各组参保人数[12]。
趋势外推法的主要步骤如下:
1)选取预测对象。本研究选取的预测对象为参保人数,该参数随年份呈上升及下降的趋势,适合用趋势外推法进行预测。
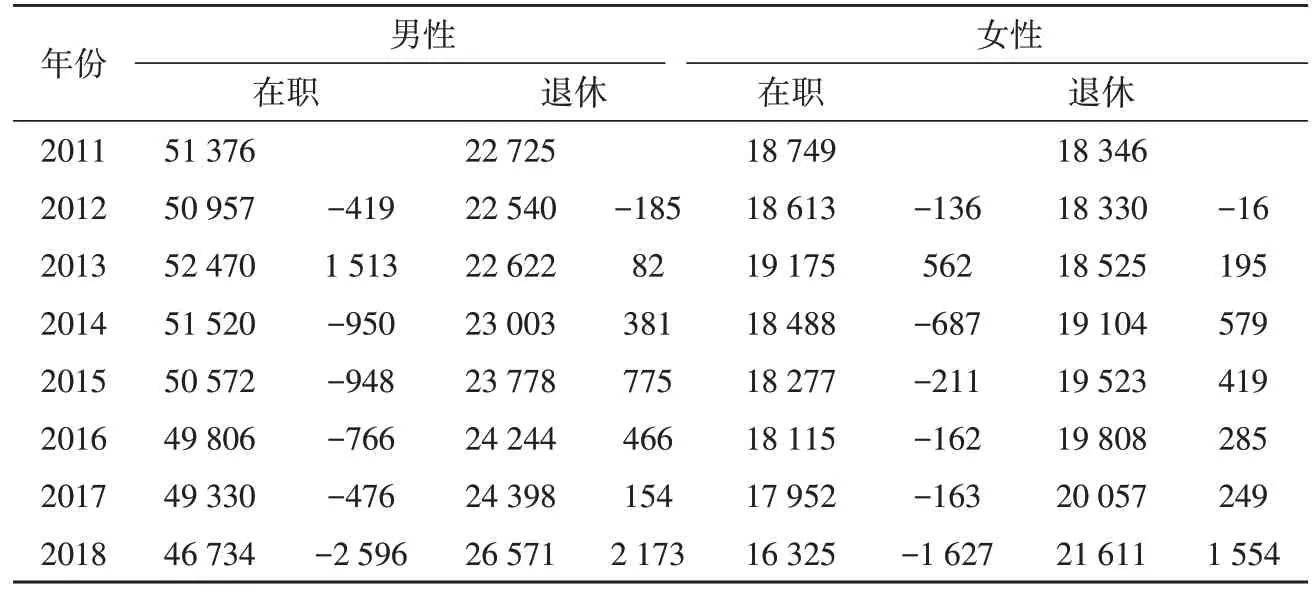
表2 2011-2018年参保人数及变化量表 单位:人
2)数据收集。采用2011-2018 年的数据,按照模型要求分为男性在职、男性退休、女性在职、女性退休四个组。
3)进行线性拟合。画出八年间各组参保人数的变化曲线,并进行曲线拟合,找到与该曲线最接近的曲线方程,可按照可绝系数选择拟合的曲线方程,越接近1,说明拟合曲线越接近实际曲线。
4)趋势外推。按照拟合曲线的方程,对未来年份的参保人数进行预测。
3 补充医疗保险精算模型的参数设定及预测
考虑到历史数据长度为8 年,为保证预测效果,以2019-2021年的数据进行预测。
3.1 各病种发病率测算
以2011-2018年各病种发病率的算术平均值做为精算模型中的发病率参数。测算结果如表3所示。
从测算结果可以看出,各病种退休人员的发病率明显高于在职人员,这是因生命周期产生的必然现象;但在性别上不存在明显的趋势性,因病种不同,各性别的发病率各有高低。
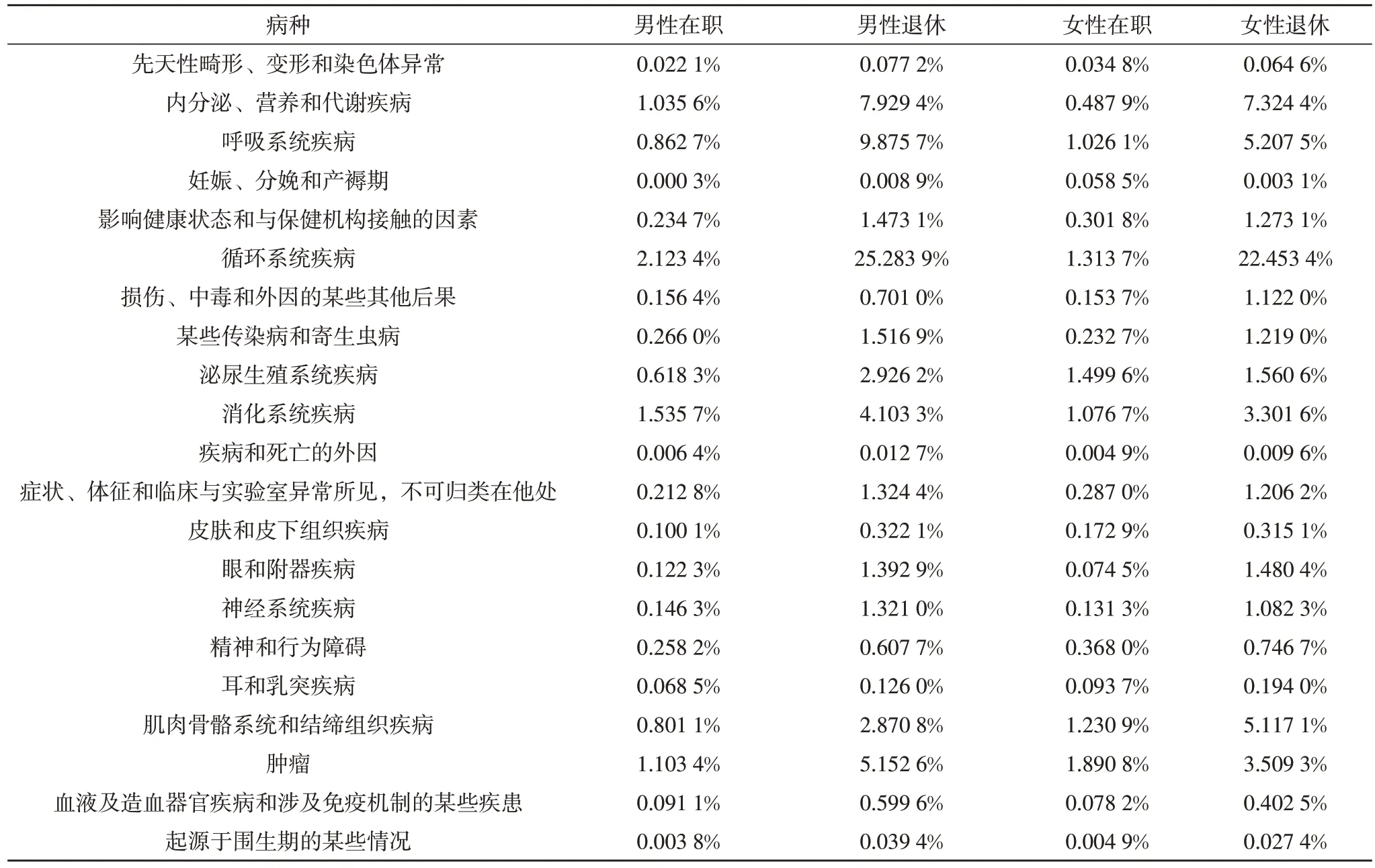
表3 按病种测算的各组发病率表
3.2 各病种次均赔付额预测
根据GM(1,1)灰度模型预测各病种次均赔付额1,预测精确度如表4所示。
从测算结果可以看出,可以发现部分病种的预测精度较好,如呼吸系统疾病、循环系统疾病、肿瘤等;但也有部分病种的预测精度较差,如先天性畸形、变形和染色体异常、损伤、中毒和外因的某些其他后果。另有部分病种,由于部分年份没有发生赔付,数据缺乏连续性,无法进行预测。
将预测结果结合各病种的发病率进一步分析可以发现,发病率较高的病种预测结果较好,发病率低的病种预测结果较差。从数值上看,预测精度低于80%的大多为发病率小于0.5%的病种。造成这一结果的原因在一定程度上可以从统计学的角度进行解释。2011-2018年,A油气公司企业补充医疗保险参保总人数每年为112 000人左右。发病率过于低的病种,则说明此类病种的样本量较小,被观测样本可能具有特殊性,并不能代表普遍情况。因此,以具有特殊性的观测值对一般情况进行预测和估计,必定会造成预测结果的不准确。
3.3 参保人数预测
3.3.1 男性在职参保人数预测
在职男性参保人数历年数据如表5 所示,对2011-2018年的男性在职参保人数添加趋势线,运用趋势外推法进行拟合,得到拟合方程为:

由公式(17)可计算得出对应年份的预测值。由于2018 年男性在职参保人数的变化存在异常,其人数变化量明显高于往年,对于这一异常变化的原因不明确,因此需要进一步修正预测结果,并对男性退休、女性在职、女性退休组做相同处理。
如果人员变动是由于企业的政策调整,且在未来将得到保持,则为弱化早期数据的影响,强化近期数据的影响,选择剔除2011 年的数据,并加入2019年的预测数据,再次拟合得到方程为:
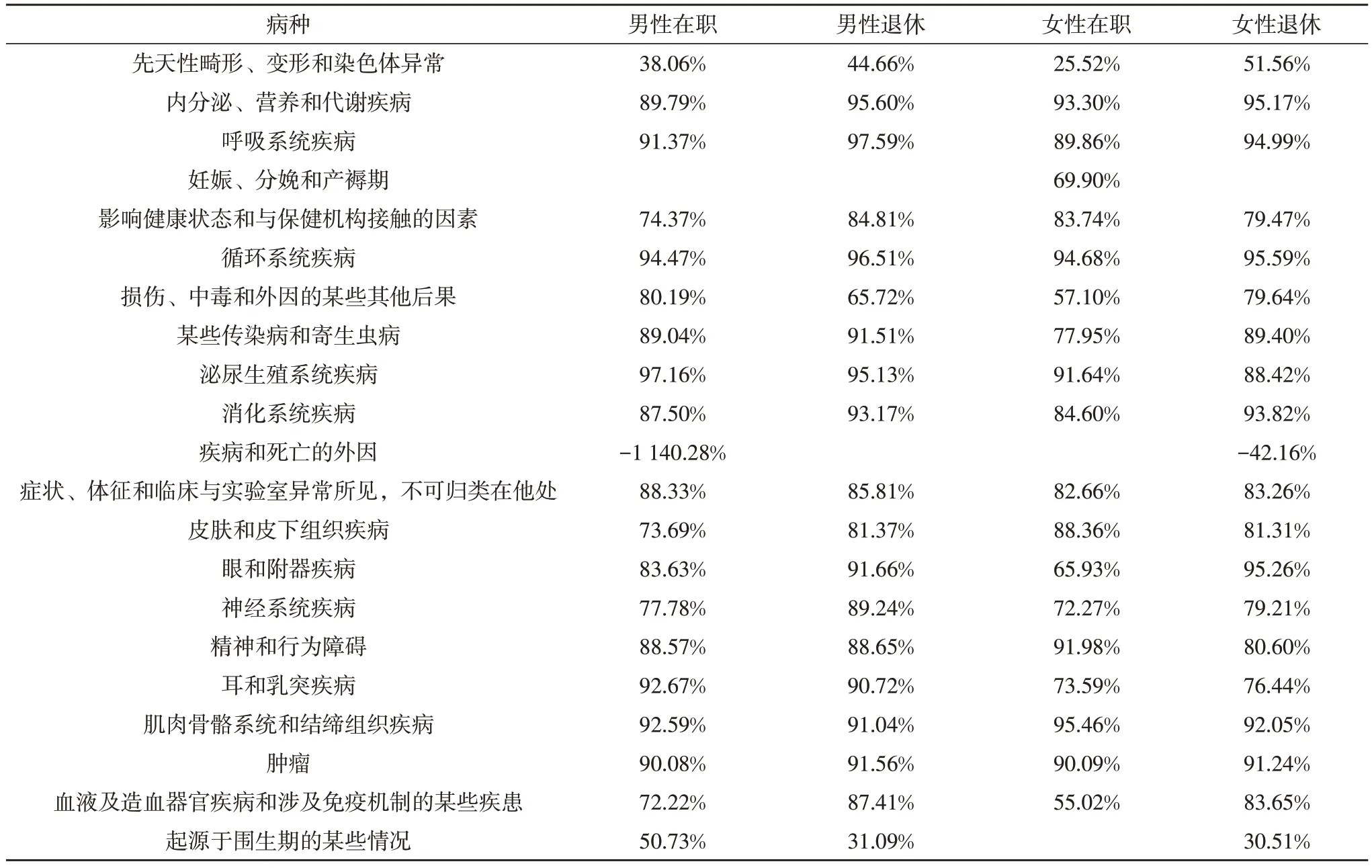
表4 各病种次均赔付额预测精度表

以(18)计算得出的2020、2021 年的男性在职参保人数作为对应年份的预测值。
若2018 年的异常现象属于计划外情况,则未来年份的变化趋势将重新回到以往水平,对于这一情况,选用内插法的方式对2019-2021年的男性在职参保人数进行预测。三种方式预测结果如表5所示。
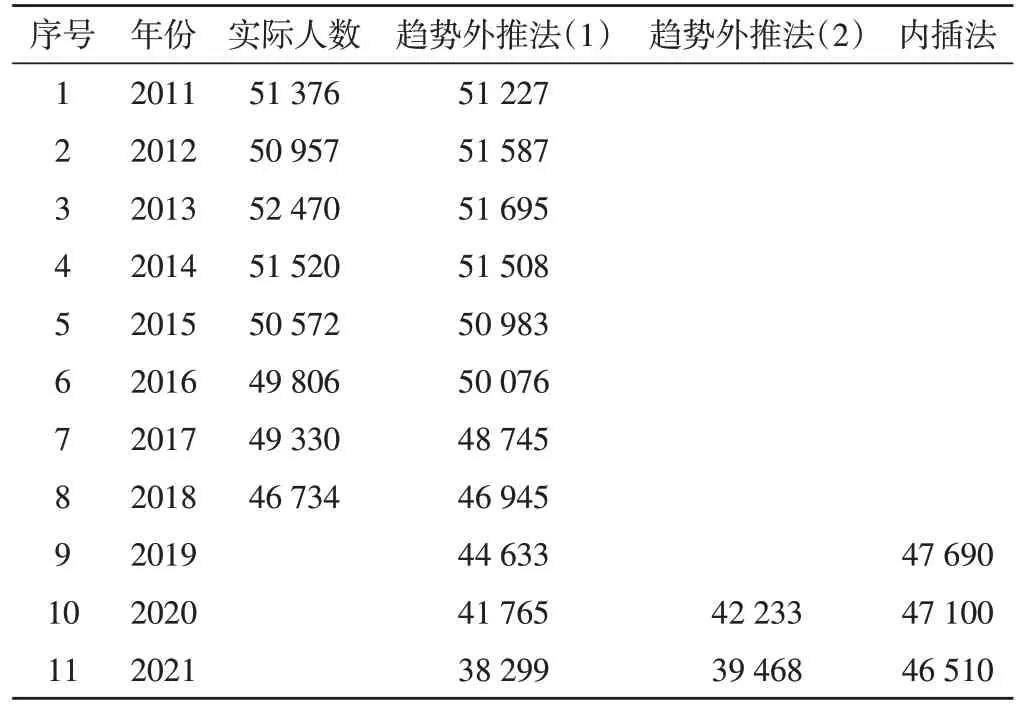
表5 男性在职参保人数预测表 单位:人
以此类推,分别对男性退休参保人数、女性在职参保人数、女性退休参保人数进行预测,预测结果如表6~表8所示。
4 补充医疗保险赔付风险预测
通过预测所得到的各病种发病率以及次均赔付额,可计算得出2019至2021年每一年人均赔付期望的预测值[13-16]。计算结果如表9、10、11所示。
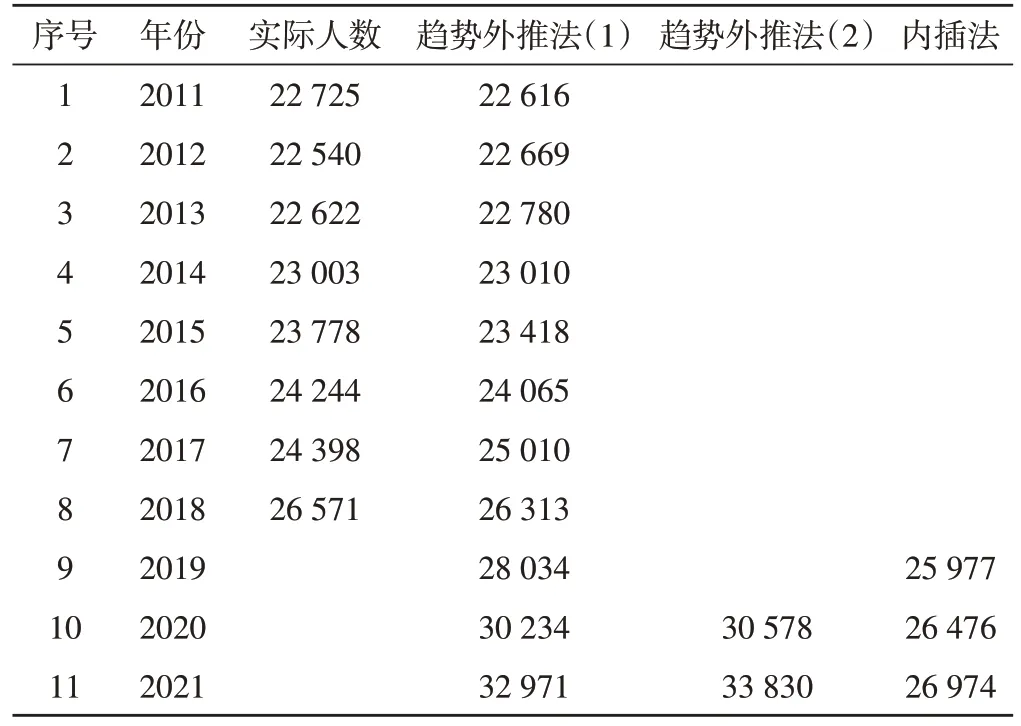
表6 男性退休参保人数预测表 单位:人
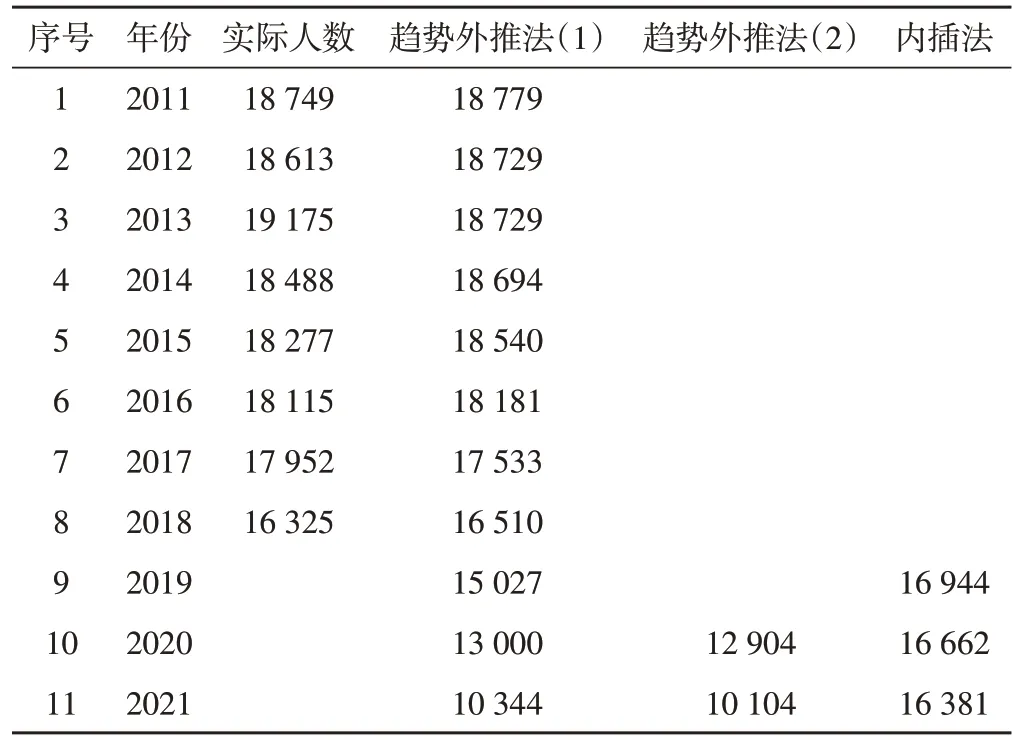
表7 女性在职参保人数预测表 单位:人
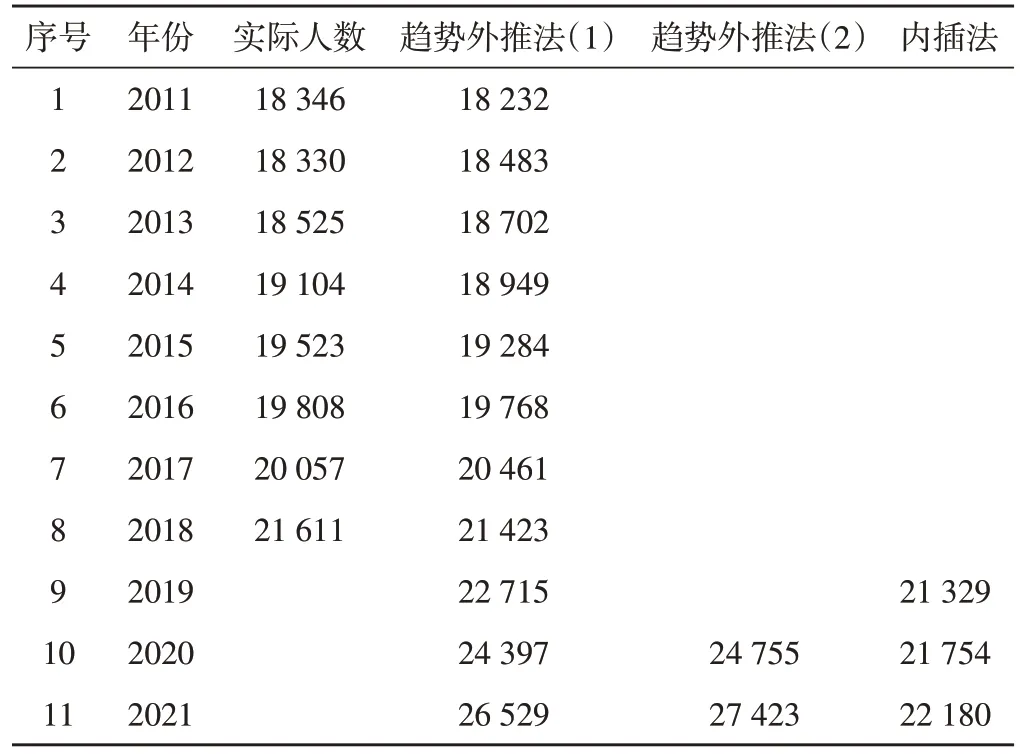
表8 女性退休参保人数预测表 单位:人
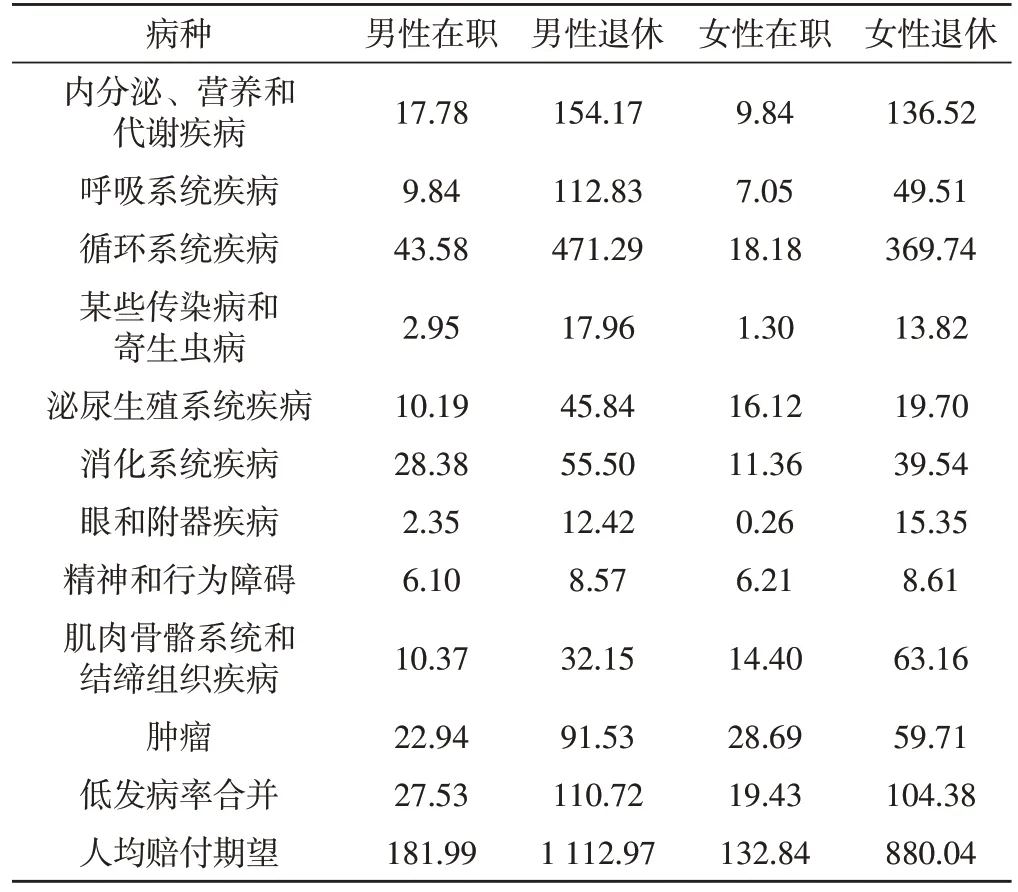
表9 2019年人均赔付期望表 单位:元
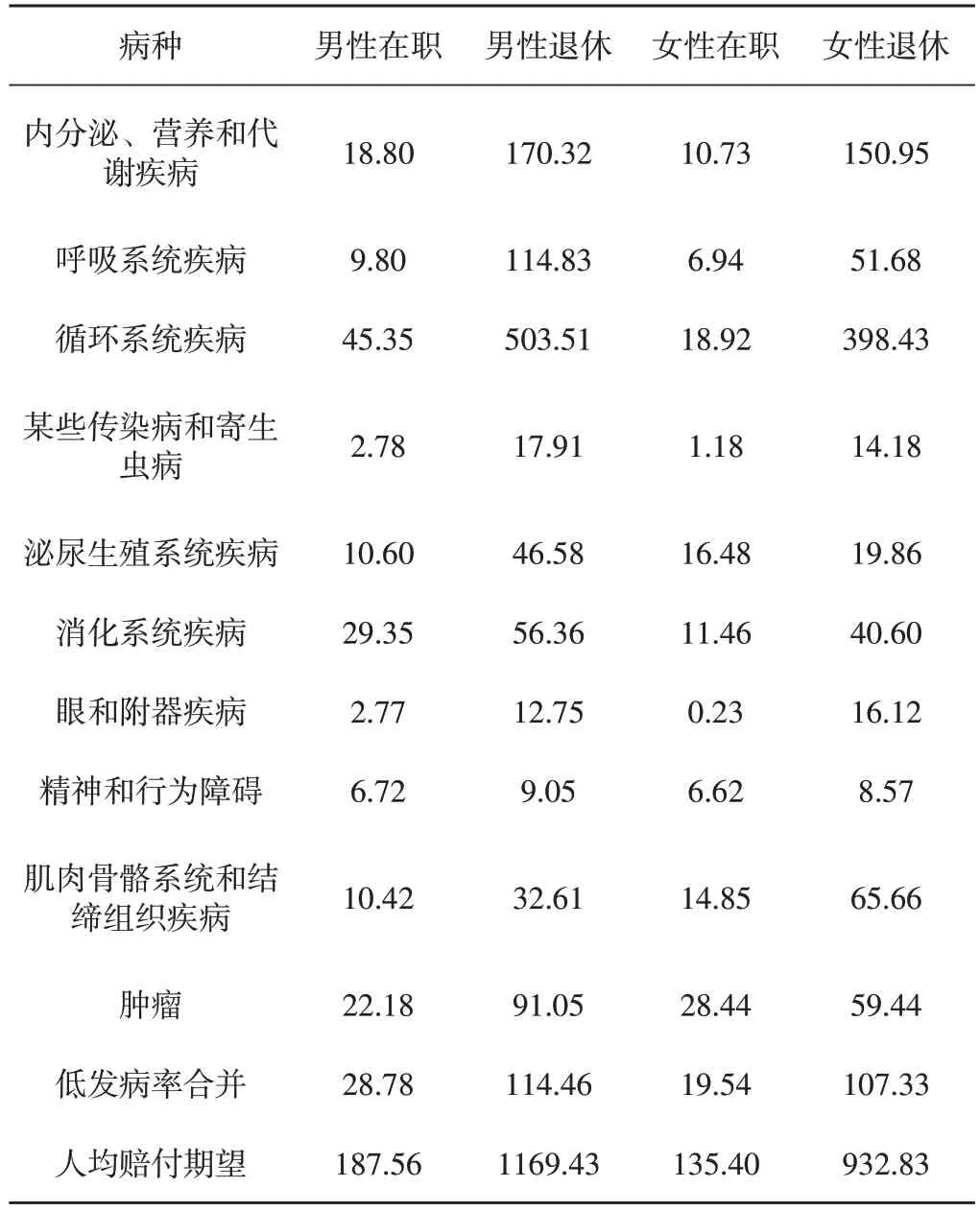
表10 2020年人均赔付期望表 单位:元
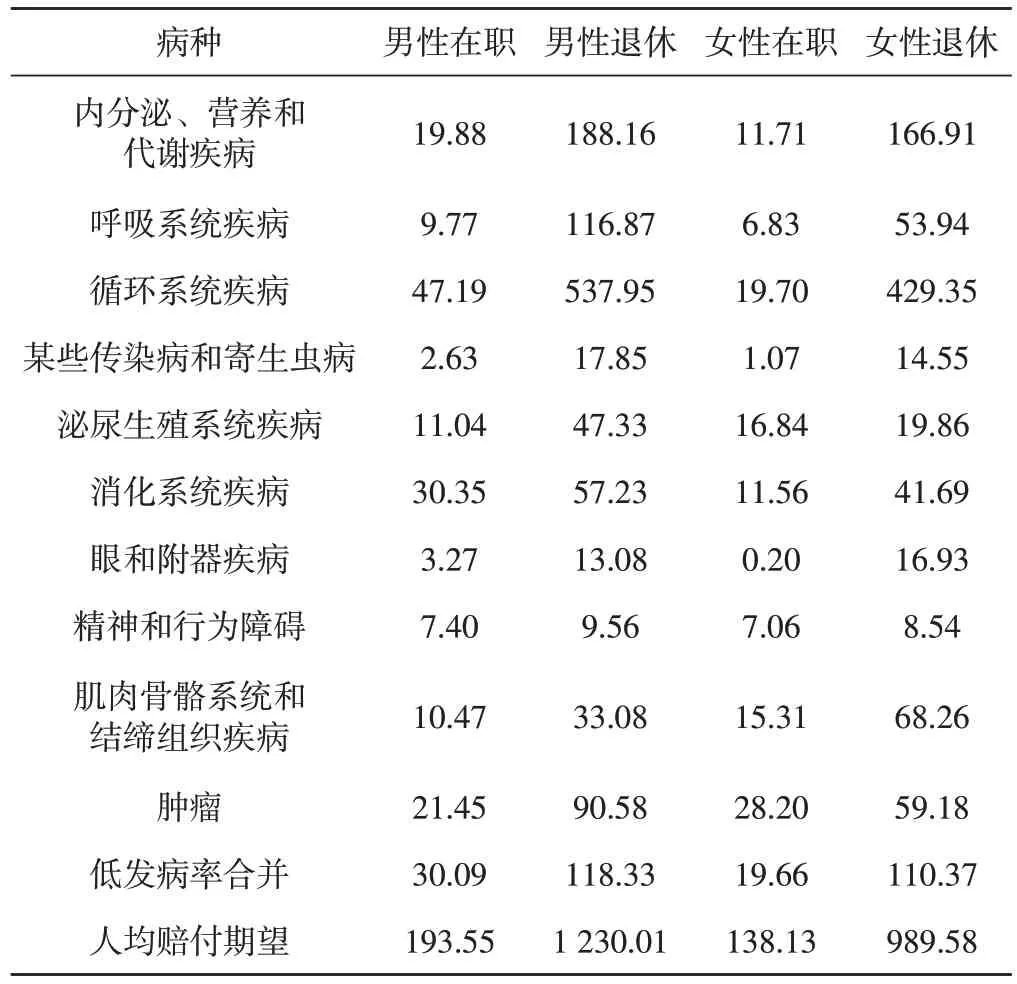
表11 2021年人均赔付期望表 单位:元
结合2019-2021年各组参保人数预测,可计算得出各年份各组的赔付额及资金总赔付的预测值。计算结果如表12所示。
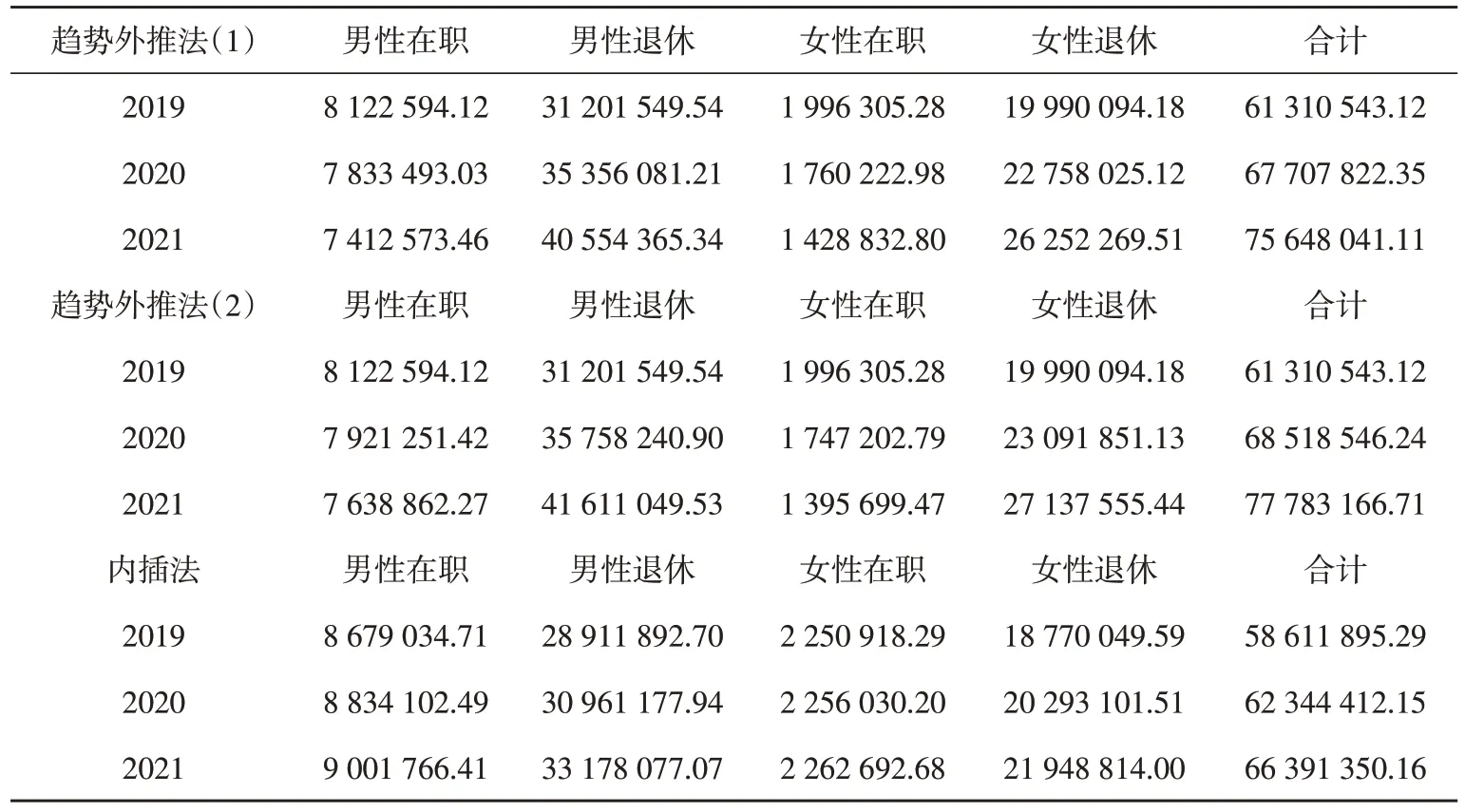
表12 2019-2021年总赔付额预测表 单位:元
2011-2021年资金实际赔付支出及预测值如表13所示,可以看到资金的赔付支出呈上升趋势。就往年实际数据来看,2018 年的总赔付额已接近2011 年的两倍,但在总参保人数上,2011-2018年并没有明显增加,始终维持在11 2000左右,参保人数数据如表14所示。
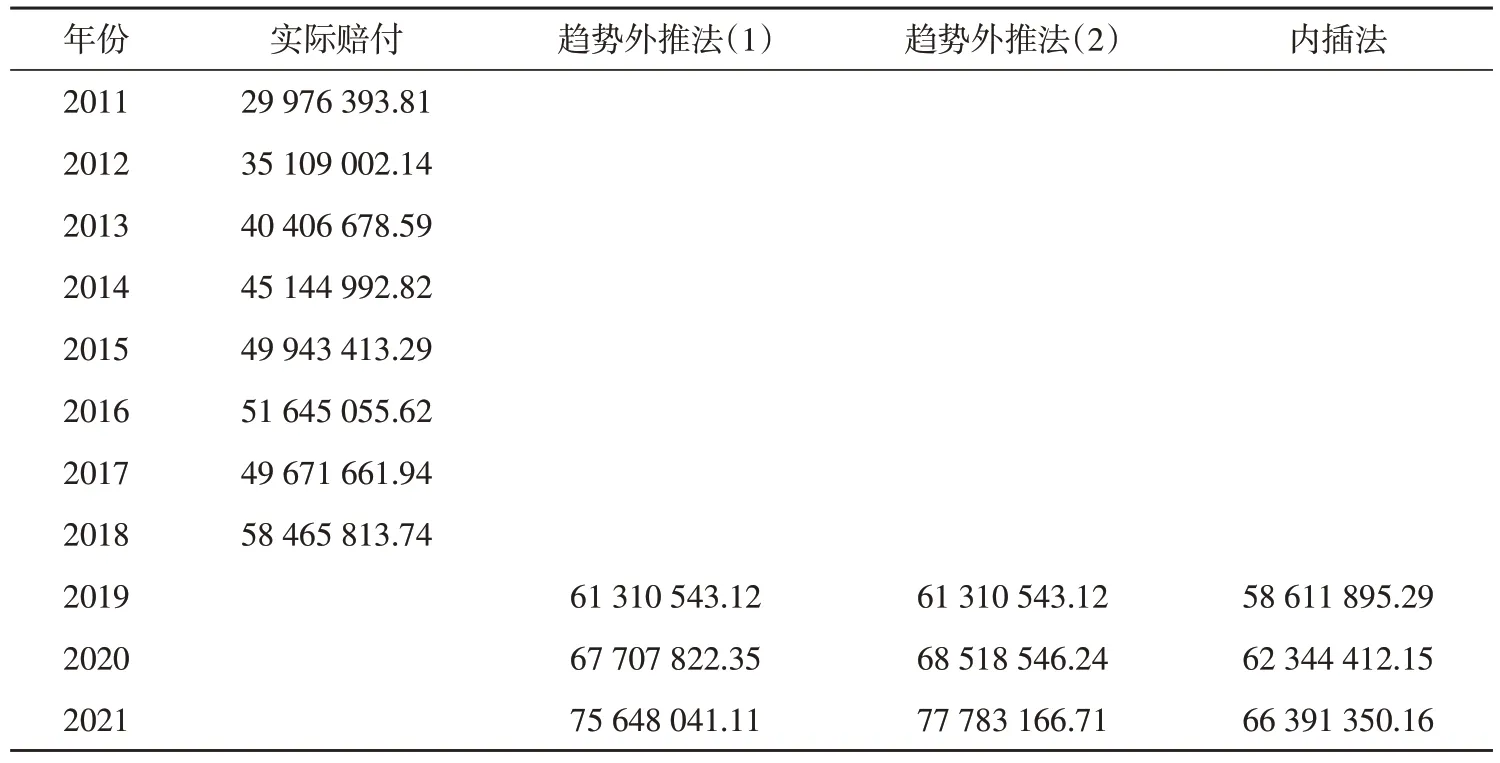
表13 总赔付支出表 单位:元
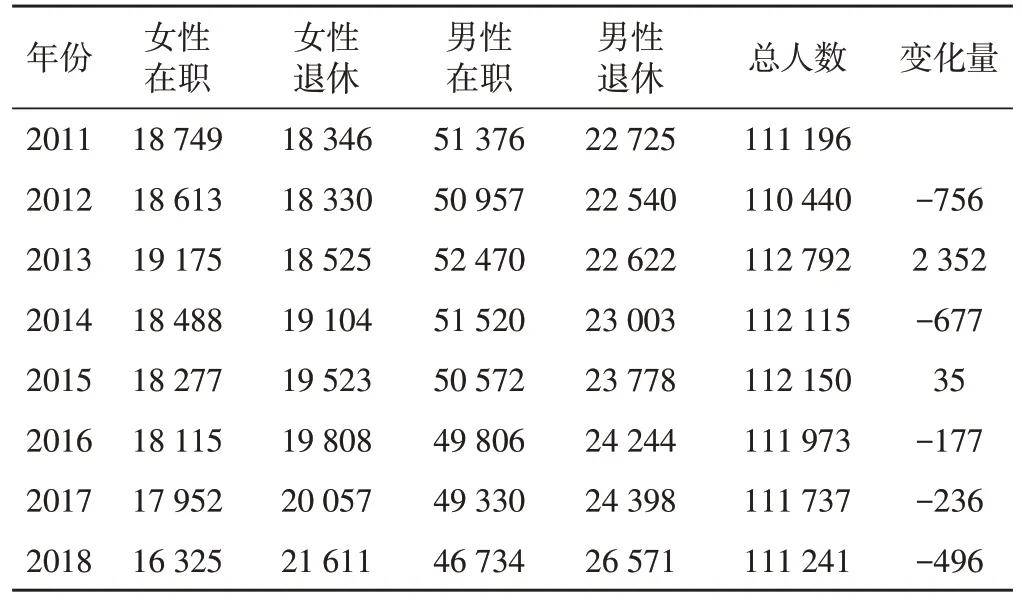
表14 历年参保人数及变化量表 单位:人
5 结论
1)造成资金总赔付支出持续增加的原因主要有两点:一方面从职工年龄结构来看,在总参保人数不变的情况下,退休人数呈上升趋势,资金总赔付支出呈持续上升;另一方面,医疗支出随时间变化总体上呈上升趋势。
2)实现了A 油气田公司补充医疗保险赔付风险预测。虽然总参保人数维持在一个较为稳定的数量,但从其内部各组的人员数量变动上来看,退休人数呈上升趋势,在职人数呈下降趋势。而退休人员的患病概率一定高于在职人员,因此会造成在总参保人数不变的情况下,资金总赔付支出呈持续上升的情况。医疗支出随时间变化总体上呈上升趋势。虽然单病种的就医支出在各年有起有伏,但在总体上,医疗支出依旧呈现上升的趋势。这也是造成资金总赔付呈现上升态势的重要原因[17-18]。

