基于复合权重的天然气需求组合预测模型的构建
张吉军 李洪兵 孙逸林 韩 咪
(西南石油大学经济管理学院,四川 成都 610500)
0 引言
天然气作为高效、低碳、清洁的优质能源,在促进城市经济高质量健康发展、保障城市社会稳定中具有重要作用。随着中国经济转向中高速发展的新常态、城镇化进程步入高质量发展的新阶段,城市天然气需求量受到了众多复杂因素的影响。在实际工作中,传统的预测方法难以实现多维影响因素的城市天然气需求预测,面对多因素的非线性抽象系统,采用任何单一预测模型难以在任何环境状态下达到令人满意的预测效果。因此,1969年Bates和Granger[1]首次提出将两个或两个以上的单一预测模型赋予相应的权重进行组合预测。组合预测模型充分地融合了各单一预测模型提供的有效信息,其目的是进一步降低预测误差[2],提高预测精度,为管理决策部门进行科学规划与决策提供准确可靠的信息数据。
组合预测模型可最大化地利用单一预测模型独特的优势,扬长避短,提高预测结果的准确性,备受国内外学者青睐,使组合预测方法得到了快速发展和广泛应用[3-5]。组合预测模型侧重于单一预测模型的某一种优势,并求解赋权,预测精度在一定程度上得到了提高。例如:陈华友等[6]以误差平方和为准则,采用IOWA算子确定组合预测权重,构建新组合预测模型;Conflitti Cristina 等[7]利用以均方预测误差(MSFE)最小为目标,计算组合预测模型的最优组合权重系数,使组合模型达到降低预测误差平方和的目的;黄魁等[8]采用有效度的概念将灰色GM(1,1)模型与神经网络模型组合在一起,对雷达发射机的故障进行预测,为装备的故障预测与预测性维修提供了支撑;叶雪强等[9]采用熵值法赋权建立组合预测模型对三峡船闸过闸货运量进行了预测,相对原单一预测模型,构建的组合预测模型提高了预测精度[10-12]。以往学者采用组合预测模型原理,仅从某一角度利用了单一预测模型的某一优势,使预测精度得到了一定提高,并未多角度地全面充分吸纳各类模型的独特优势。
针对众多复杂影响因素干扰的城市天然气需求量预测,采用能实现拐点预测具有非线性逼近预测功能的复合权重组合预测模型更能实现“早期”的精准预测,且非线性的组合预测方法较线性组合预测更优,组合预测模型的预测精度更高、预测结果更稳定[13]。基于此,以精度排序、误差大小、离散程度为准则,对灰色GM(1,N)模型和多元线性回归模型赋权进行融合,构建不同视角标准的组合预测模型。再采用改进的灰色关联度确定复合权重系数,将不同刻画标准的组合预测模型进行融合,全面充分有效利用各类预测模型的优势,建立多维影响因素环境下具有非线性预测性能的复合权重组合预测模型,实现非线性逼近预测功能的拐点预测,提高城市天然气需求量“早期”预测的精度。
2 相关理论
2.1 灰色GM(1,N)模型
灰色预测模型在一定程度上能很好地适应天然气需求的非线性增长特征[14],灰色GM(1,N)模型是多变量灰色预测模型,它的建模对象由一个系统特征行为数据序列和N-1 个相关因素行为数据序列组成,建模过程充分考虑了外界环境变化对系统变化趋势的影响,在考虑了多维信息环境的情况下可使信息数据预测更具现实意义[15]。多变量灰色预测模型克服了单变量灰色预测模型预测能力有限的缺点,能更精准地刻画外界环境变化对系统内部的影响。

为系统特征行为数据序列,而
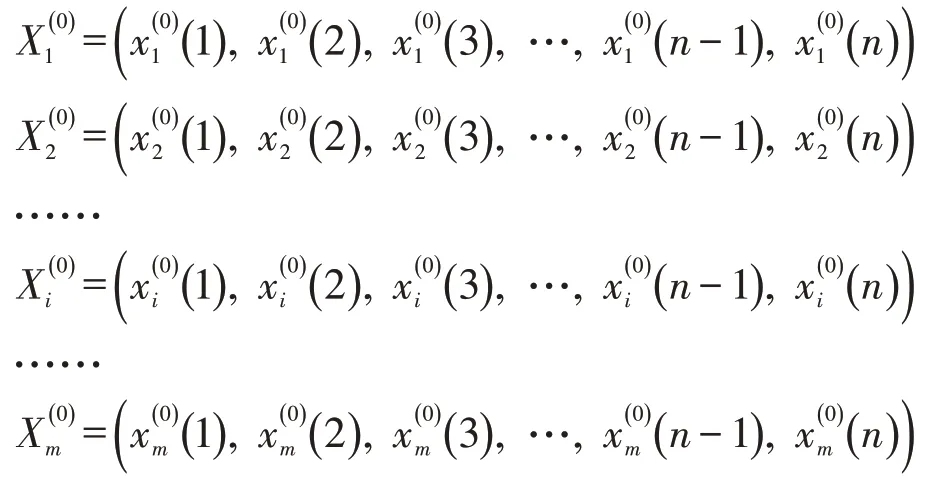

为GM(1,N)模型。其中,城市天然气需求量的系统发展系数为-a,驱动系数为bi,驱动项为参数列为利用最小二乘法求解参数列,可得:
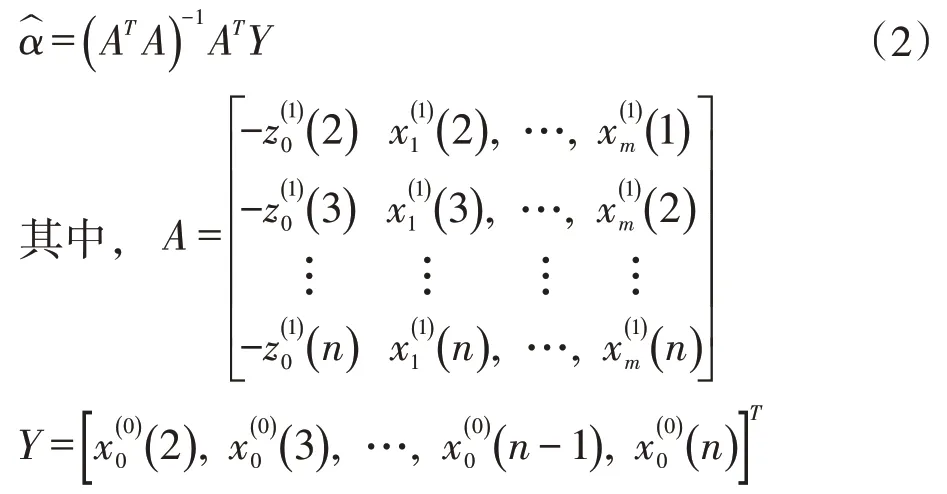
设GM(1,N)模型的白化方程为:
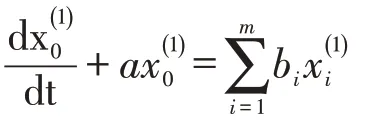
则GM(1,N)模型的近似时间响应式为:


2.2 多元线性回归模型
回归分析是由英国统计学家和生物学家Francis Galton 于19 世纪末首次提出,能揭示解释变量与被解释变量之间的内在关系。多元线性回归模型可刻画一个被解释变量与多个解释变量之间的线性内涵关系,其函数形式如下:
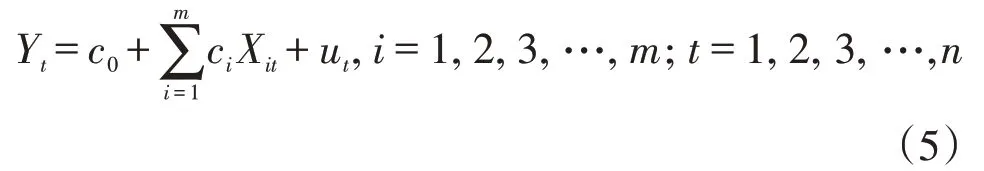
其中,Y为被解释变量,Xi为第i个解释变量,c0为常数项,ci为偏回归系数,ut为随机误差项。利用最小二乘法进行模型参数c0与ci的估计。
2.3 误差平方和倒数法
根据单一预测模型预测误差的大小确定单一预测模型权重系数,令各单一预测模型的误差平方和为Ei,x(0)(t)为实际值,为单一预测模型的预测值,则:

单一预测模型的组合预测权重系数ωi为:

2.4 简单加权平均方法
根据结果组合法原则,利用简单加权平均方法确定单一预测模型权重系数,将两个及以上的单一模型组合在一起,构建新模型对未来进行预测。
首先将反应各单一模型预测精度大小的误差平方和Ei(i=1,2,3,…,k)从大到小依次进行排序,假设E1>E2>…>Ek,根据单一模型预测误差与其权重系数成反比的基本原理,故排序越在前的单一模型,组合预测中的权重系数就应越小,则依据精度大小排序的单一模型的组合预测权重系数ωi为:
2.5 熵值法
从信息论的观点出发,根据各单一预测模型预测结果的变异程度,采用信息熵的原理,计算各单一预测模型的权重系数。单一预测模型的熵值越大,其蕴含的信息量就越小,变异程度就越小,反之越大。采用熵值法[13]确定组合预测模型权重系数的步骤如下:
(1)归一化单一预测模型的相对误差εit,且x(0)(t)为实际值,为单一预测模型的预测值,则有:

(2)计算单一预测模型预测结果的熵值为:
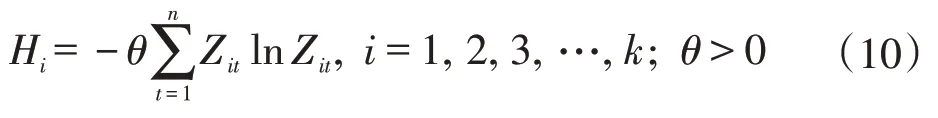
(3)计算单一预测模型的变异程度系数Di为:

(4)计算单一预测模型的权重系数ωi为:
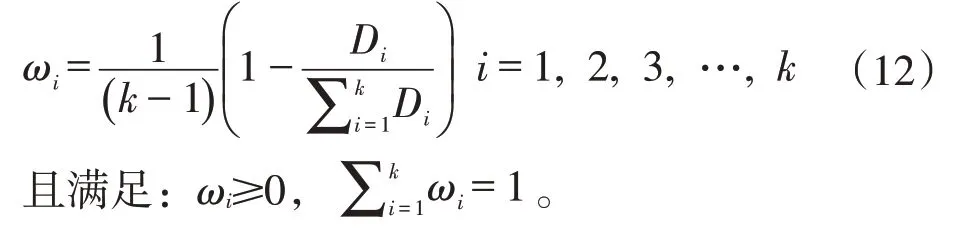
3 基于复合权重的组合预测模型构建
不同的预测模型从不同的角度、不同的层面在一定程度上揭示预测对象的演变规律。组合预测模型就是最大程度上利用单一预测模型的优点,克服不足,以提高预测的精度和预测结果的稳定性。灰色GM(1,N)模型具有将多维度的“灰信息”以指数内涵形式进行刻画描述;多元线性回归模型以多维度的信息为解释变量,刻画与被解释变量的线性内涵关系;简单加权平均方法是采用精度大小排序的一种非等权平均方法,确定组合预测模型权重系数;误差平方和倒数法采用预测误差平方和的大小确定组合预测权重系数;熵值法根据单一预测模型预测结果的离散变异程度确定组合预测权重系数。运用误差平方和倒数法、简单加权平均方法、熵值法分别将灰色GM(1,N)模型与多元线性回归模型进行融合,构建不同视角的组合模型。为进一步充分吸纳各类预测模型的优势特征,根据实际值与预测值数据序列的几何曲线演变趋势越接近应赋予较大权重系数的原理,采用灰色关联度确定从不同视角构成组合模型的权重系数将组合模型进行融合,构建基于复合权重的组合预测模型,构建框架流程图如图1所示。
运用灰色关联分析法的邓氏灰色关联度[14-15]确定组合权重,在确定组合预测模型权重过程中,各数据序列的属性相同,而利用传统初值像的方法对原始数据序列进行无量纲化处理(传统初值像处理的公式为并非以相同的度量标准刻画实际值与预测值数据序列的几何曲线演变趋势。当数据序列成倍数关系时(X0=τXl,τ∈R+且τ≠1),邓氏灰色关联度为1,误差较大,却赋予了较大权重,导致不符合精度越高的单一模型应赋予较大权重系数的组合预测赋权基本原则。采取固定参照值的方法不仅可以避免传统初值像处理方法的不足,而且不会因增添新数据致使度量标准发生变化而需重新定义,使确定的组合权重系数值更符合实际,并满足组合预测赋权基本原则。
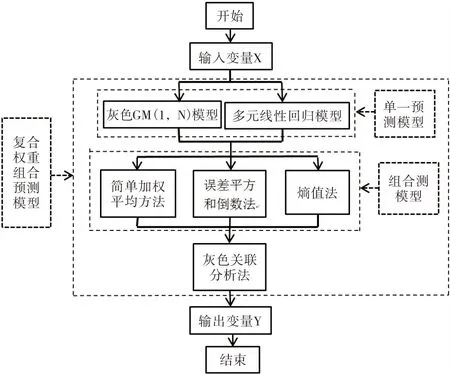
图1 基于复合权重的组合预测模型构建框架流程图
改进的邓氏灰色关联度确定组合模型复合权重的步骤如下:
1)采用固定参照值对原始数据序列进行无量纲化处理
利用固定参照值为各数据序列的参考点刻画其几何曲线演变趋势,令实际值数据序列为参考数据序列X0,参考数据序列X0的第一个值x0(1)为固定参照值,预测值数据序列为被比较数据序列Xl。则各数据序列的无量纲化序列为:

2)计算参考数据序列与各被比较数据序列的无量纲化序列对应分量之差的平方序列
参考数据序列与各被比较数据序列的无量纲化序列差值体现了几何曲线之间差异性程度,将差值进行平方处理便于凸显几何曲线的差异性程度。
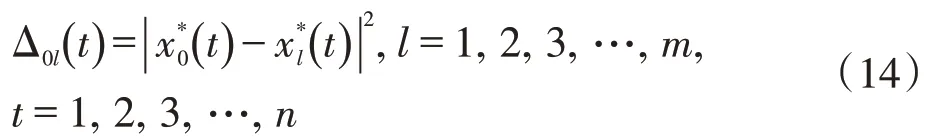
3)求Δ0l(t)的最大值与最小值,分别记为

4)计算关联系数
对绝对差值数据序列Δ0l(t)进行如下变换:

其中分别率ρ∈(0,1),一般取分辨率ρ=0.5。
5)求关联系数的平均值即为灰色关联度
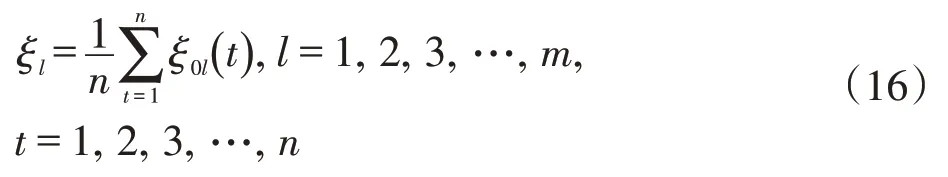
6)确定组合预测模型复合权重系数

基于复合权重系数的组合预测模型为:
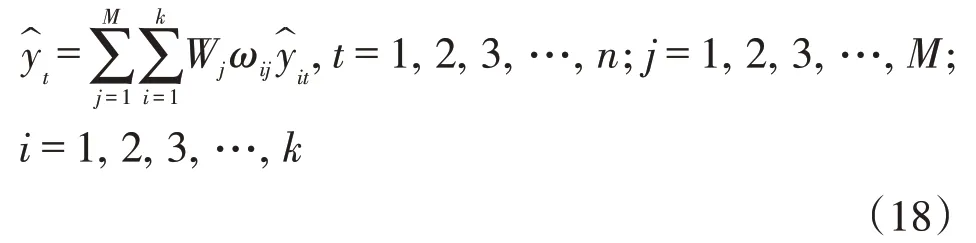
其中,为第t时期的预测值,Wj为第j种组合预测方法复合权重系数,ωij为第i种单一预测模型在第j种组合预测方法中的权重系数,为第i种单一预测模型在第t时期的预测值。
4 城市天然气需求量预测分析
4.1 数据信息搜集整理
受众多复杂因素影响的城市天然气需求量预测是动态随机的非线性抽象系统。在综合以往学者研究成果的基础上[16],选取城市燃气普及率、城镇人口、城镇化率、国内生产总值、城镇居民消费水平等对城市天然气需求有重大影响的若干因素作为变量。通过国家统计局获取2004-2018年中国城市天然气需求量及影响因素的数据信息,根据2004-2015年的信息数据,采用多维影响因素的组合预测模型进行拟合,构建复合权重的组合预测模型对2016-2018年中国城市天然气需求量进行预测,检验复合权重组合预测模型的实用性,再对2025 年中国城市天然气需求量进行预测。具体数据信息如表1所示。
4.2 预测与结果分析
根据表1中的数据信息,对2004-2015年中国城市天然气需求量进行拟合预测,并构建多维影响因素的复合权重组合预测模型,拟合结果如图2 所示。由图2可知,多维影响因素的复合权重组合预测模型具有非线性逼近预测功能,实现了城市天然气需求量的拐点预测,拟合预测的平均相对误差为2.46%,具有较好的预测性能。再采用该多维影响因素的复合权重组合预测模型对2016-2018年中国城市天然气需求量进行预测,预测结果如表2所示。通过分析可知,多维影响因素的复合权重组合预测模型平均相对误差为1.29%、误差平方和为1 283.29,提高了预测精度,预测结果更稳定,接近于实际值,预测结果可作为建立天然气供需平衡动态机制提供科学依据[17]。
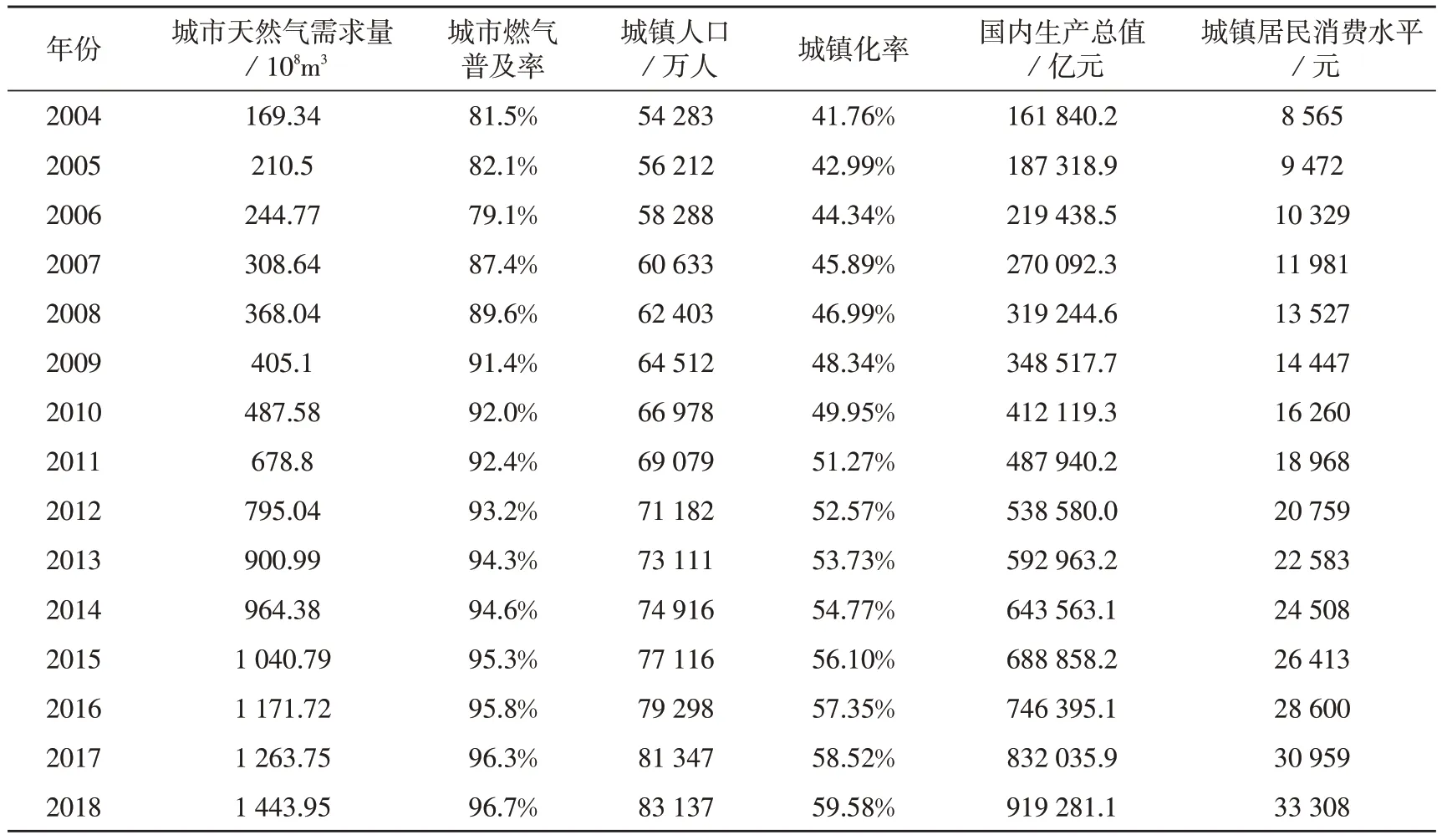
表1 2004-2018年中国城市天然气需求量及影响因素的数据信息表
根据表1中的数据信息,利用时间序列预测性能较好的经典灰色GM(1,1)模型[17]对影响因素2019-2025 年数据信息进行预测,并运用基于复合权重的组合预测模型对2025 年中国城市天然气需求量演变趋势进行预测,如图2 所示。预测结果显示,虽然2020 年受新冠肺炎疫情影响,中国城市天然气需求量增速降到了8%,中国城市天然气需求量年均增长率由16%降至10%,但中国城市天然气需求量仍呈现持续增长趋势。自2021 年起城市天然气需求量增速恢复到10%以上,到2025 年中国城市天然气需求量将达到2 884×108m3。随着碳达峰目标的严格落实,天然气需求量将持续高速增长[18-19],未来五年中国城市天然气需求量有望达到3 000×108m3。未来天然气在能源体系中将占主体地位,其发展已进入黄金时代[19],相关企事业部门或城市管理者可根据预测结果进行科学购气、储气、调峰调压等决策,确保城市重要领域或地区的用气安全,为城市经济可持续健康发展和社会稳定保驾护航。

表2 2016-2018年中国城市天然气需求量预测结果表 单位:108m3

图2 中国城市天然气需求实际演变趋势与预测演变趋势图
5 结束语
目前,对于受众多复杂影响因素的非线性抽象系统的复合权重组合预测模型仍在进一步探索之中,在利用简单加权平均方法、误差平方和倒数法、熵值法将灰色GM(1,N)模型与多元线性回归模型进行组合的基础上,采用改进的邓氏灰色关联度确定复合权重系数,构建了一种新的多维影响因素的复合权重组合预测模型,实例证明它具有实现拐点预测的功能,降低了误差,提高了组合预测模型的预测精度,具有良好的预测性能。灰色关联分析法根据几何曲线演变趋势计算关联度,有益于将预测模型的独特优势延续到未来预测中,使复合权重组合预测模型充分地将各类预测模型的有用信息进行有效融合,达到结果组合预测模型进一步降低误差的目的。在复合权重组合预测模型构建框架的基础上,可以进一步探索运用人工神经网络、SVM 以及采用有效度原理、AHP、二项式系数法等确定组合权重的方法建立复合权重组合预测模型。

