不同管径水平管道气液两相流动数值模拟
张赫铭,李文昊,何新林*,刘宁宁,金瑾
(1. 石河子大学水利建筑工程学院,新疆 石河子 832000; 2. 石河子大学现代节水灌溉兵团重点实验室,新疆 石河子832000)
压力管道输水在正常运行时会经常出现由于气体存在导致爆管等问题,因此需要对含气管道输水过程进行研究.一些学者研究了单一液相条件下的管道流动,而在较平坦管道的初次充水和平稳流动中,由于初次充水无法排净管中气体,管道流量调节时的负压注气,水泵吸入空气等都会使管道呈现多相流的运动特点[1].周晋军等[2]对管道凸起段气囊运动的水力特性进行了分析,认为弯折位置处的气囊随着水量的减小而增大,并且会对水流产生更大的阻力.郭永鑫等[3]通过模型试验和理论结合,认为南水北调模型中滞留气泡对输水能力的影响较小,可忽略.叶宏开等[4]提出了气体释放-离散模型用于计算管路中有气泡时的水锤升压,并通过试验验证.
不同的气液流量对应着不同的流型,管径的变化也会对流型产生一定影响,由于无法肉眼观测实际管道内流体的运动,对流型的研究主要为试验和模拟2部分,并认为水平管中会出现泡状流、塞状流、分层流、波状流、弹状流、环状流、雾状流7种流型[5].流型图是用于识别流型及进行流型转换判断的重要手段之一,早期MANDHANE等[6]提出了水平管流型图,后随着研究的深入,不同学者对流型图进行了修正[7].然而由于人为的主观因素性,导致对试验现象的观测结果各有不同,因此修正的流型图也不尽相同.随着试验条件的优化,国外学者[8-10]多通过试验用电导探针、热膜风速仪完成气液两相流各重要参数的测量.Fluent作为一种可靠的模拟软件因较好的网格能力、精确性、可靠性、并行能力和后处理而多被用于管道科学研究[11].卢坤铭等[12]通过三维CDF模拟了管道水流对管内气团的压缩变形;陈江林等[13]通过试验加模拟的形式,研究了T型三通管不同工况下的水头损失,并认为数值模拟结果与试验结果可较好地吻合.对于两相流的模拟多集中在竖直管径和较小管径中[14].
国内对于灌溉管道模拟多为单相流,对传统气液两相流的研究多通过试验方法,由于气液两相分布的不对称性,不同直径管道中水平两相流的相对运动和流型转变特性可能存在差异.且相比于一维模型,三维管道模型能得到更为准确的两相流各项水力参数.文中基于计算流体动力学软件进行不同管径下气液两相流的三维瞬态模拟,并用曼德汉流型图进行验证,得出水平管道中不同管径,液相折算速度下的流型及转化关系,并进行流场的压力、流速分析,结论可为实际工程中有压管道的设计和管道气液两相流研究提供理论依据.
1 水平管道气液两相流数学模型
为更好地监控不同时刻的两相分布,文中选用VOF模型,一种表面追踪方法,可较好地追踪一种或多种相互不相容流体间的交界面.
1.1 前处理几何模型
结合新疆生产建设兵团第十三师输水管道部分干管进行研究,选择水平管道作为研究对象,建立几何模型.最终确定模型管道管长l=3 m,管径D=0.16,0.12,0.08 m.气体通过混合入口段使整个管道成气液两相流状态,其中液体流速为2~6 m/s,气体流速为0.2~0.5 m/s.最终建立几何模型如图1所示.

图1 管道几何模型示意图
后利用ICEM-CFD对几何体进行网格划分,针对圆柱体三维管道几何结构,选用O型剖分和六面体结构网格进行划分,以提高网格质量.最终网格单元数分别为750 210,541 693,407 398.其中计算域内所有网格的网格单元质量均大于0.7. 文中 0.12 m管径下网格划分图如图2所示.
研究模拟9种工况条件下的气液两相流过程,为气泡流到塞状流的过渡.表1为不同工况条件下的各参数值,其中jg和jf分别为水平管道中的气相及液相折算速度[5],定义为
(1)
式中:j为混合折算速度;Vg和Vf分别为气体和液体的容积流量;A为流道截面积.

图2 网格划分

表1 9种工况下的模拟条件
1.2 数学计算过程
1.2.1 控制方程
水平管道气液两相流问题的数学模型的VOF及标准湍流方程的控制方程如下:
体积分数的连续性方程式为
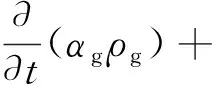
(2)
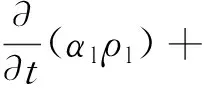
(3)
αg+αl=1,
(4)
动量方程式为
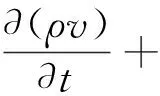
(5)
标准湍流方程式为
Gb-ρε-YM+∅k,
(6)
(7)
1.2.2 选择求解器、参数设置及求解方法
选用基于压力求解器进行瞬态模拟,并添加重力项.气相为可压缩空气,液相为不可压缩水,且无能量、质量传递.添加空气项时设为ideal air,可压缩空气的物性参数包括:比热cp=1 006.43,动力黏度μ=1.79×10-5.求解方法基于PISO压力速度耦合算法;梯度项选用基于最小二乘法格式;压力差值选用PRESTO格式项;为简化计算,动力指数、湍流动能、湍流耗散率、水平集函数均选用一阶迎风格式;体积分数差值选择几何重建格式.
1.2.3 边界条件和初始条件
由于气体的可压缩性,因此入口边界条件设置为混合质量流量入口;边界入口压力为大气压,出口设为压力出口边界;选择标准初始化,从管道入口开始,初始管道中水的体积分数设为1,认为0时刻管道充满水;湍流参数设置选用湍流强度及水力直径项并根据入口混合质量流量的大小计算;各项残差均设为1.0×10-3.
2 模拟结果及分析
2.1 模型准确性验证
1974年曼德汉根据近6 000个试验数据归纳出一幅适用于判别内径为12.7~165.1 mm水平管中气液两相流的流型如图3所示,其中纵坐标为液相折算速度,横坐标为气象折算速度.根据模拟结果显示气相折算的速度为0.3 m/s,液相折算速度分别为5,3 m/s时的模拟结果流态图分别为泡状流和塞状流,和曼德汉流型图对应良好,可以应用到三维管道水平气液两相流的模拟计算.
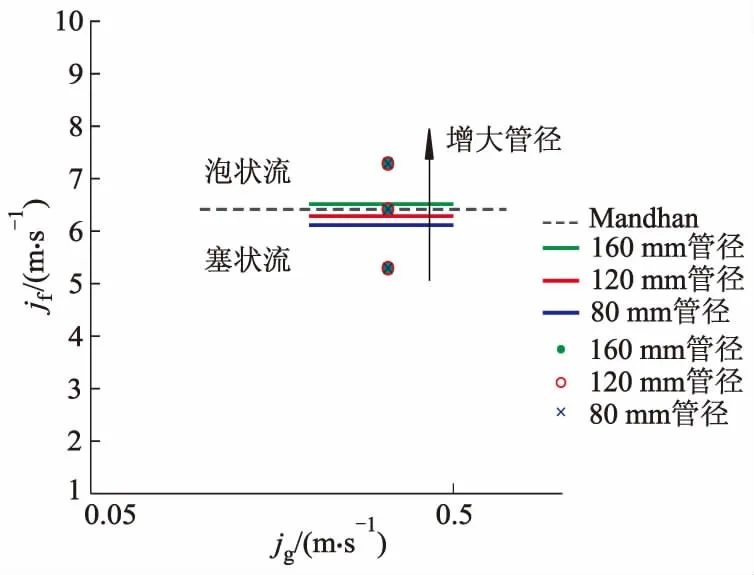
图3 曼德汉流型图
2.2 充液过程气液流动状态分析
在一定气液折算速度下,适当减小液相折算速度可得到气泡流到塞状流的过渡,随着充液时间的增长,不同流型下气泡形成过程也不同[16].以160 mm管径为例,图4为1.35 s时刻,当jf从5 m/s降低到3 m/s时,该管径下不同流型(气泡状态)的气液两相分布俯视图,图中φ为气相体积分数.

图4 jf减小时管道气液两相分布俯视图
当jf=5 m/s时,初始阶段由于气体均匀散布在液体中,两相掺混较为明显,气体没有明显的边界,此时气体主要随着液体向前运动.随时间增长,由于浮力的作用,气泡向管道顶端聚集,气液两相间相互作用增强,最终形成气泡流,如图4a所示.随着jf降低,气泡流量相同时,由于流速的降低,水对气体携带能力减弱,气体由于自身密度更快的移动到管道顶部,并聚集成大气囊,由于液相折算速度较大,大气囊被打破并形成断续的细长气囊.对比方案1,随着液体流量的降低,湍流混合作用的减弱,在管壁附近堆积的气泡更集中在顶部壁附近,并形成细长气泡,此时为气泡流-塞状流的过渡,如图4b所示.随着jf进一步减小,气泡由细长气泡过渡到塞状泡.初始阶段气液更快速分离,并形成较清晰的分界面,小气泡相互融合形成较大气泡,随着时间的推移,由于液体的作用力,大气泡逐渐变为细长气泡,多个细长气泡相互融合形成具有塞状流特性的大气泡,如图4c所示.
2.3 不同管径下的流型变化分析
图5为1.35 s,1.40 s,1.45s时刻160,120,80 mm管径下随着jf的减小,气液流动过程的流型剖面图,发现不同管径下气泡分布的演变经历了相似的过程,均产生了泡状流到塞状流的过渡,不同的是不同管径两相流型过渡时对应着不同的临界液相折算速度.

图5 不同管径气液两相剖面图
当jf=5 m/s时,对比图5a,d,g这3种管径中的流型均为气泡流,且管径越大,气体分布越均匀.当jf降低到接近过渡的状态时(jf=4 m/s),对比图5b,h,发现160 mm管径下气体更均匀地分布在管道上表面且部分相互聚集融合;而80 mm管径下的气体仍以大气泡的形式存在.进一步减小jf发现160,120 mm(见图5c,f)管径下呈明显的塞状气泡,且气泡长度较长,更贴近上壁运动;80 mm(见图5i)管径下的塞状气泡较短,且和上壁间存在小气泡.
由此得出结论:随着管道尺寸的增加,在jg=0.3 m/s时,气泡流-塞状流过渡的起始点移向更高的折算液体速度,从80 mm管道中的小于4 m/s(方案9)移到160 mm管道中的4 m/s(方案4).而同一液相折算流速下管道直径的增加时,液体雷诺数增加,此时管道湍流强度增加,认为此时流场更紊乱,与此结论不符.通过分析认为管径的增大除了增大变雷诺数,管道自身曲率也会减小,通过对比相同折算速度条件下不同直径管道的气液两相分布图时,发现大管径管道中的气泡更紧密地堆积在管道上部分,气泡之间的距离小,小气泡间更易聚合成大气泡,气泡层占据了更小的管道面积,紊流强度降低,更易形成塞状流,而小管道中的气泡分布则更加分散,不易形成塞状流.
2.4 折算速度对管道压力波动的影响研究
图6分别显示了5种方案下,不同位置测压点的压力折线图,其中L为从原点开始沿z轴正方向的距离.由图可知,由于气团具有周期性,即使在气液两相流动稳定的情况下,气泡流和塞状流运动依然为非稳态,表现为初始压力和速度变化较大,随着时间的推移,气液两相间混合均匀,压力波动逐渐平稳,其中1.0 m位置处的测压点压力波动最为剧烈,最大压力值为115 177.6 Pa,最大压差为23 132.9 Pa;1.9 m位置处的测压点压力波动略小于1 m处的压力波动,最大压力值为111 012.2 Pa,最大压差为19 842.1 Pa;2.8 m位置处的测压点压力波动最小,最大压力值为104 875.8 Pa,最大压差为9 437.1 Pa.为保证压力测量的准确性,尽量选择两相混合均匀位置处(即管道末端位置)进行压力的测量.方案3,6,9随着液相折算速度的减小,压力峰值减小,最大压差相应减小.方案7,8,9显示同一气、液折算速度下,随着管径的减小,压力波动也会相应减小.由于气团的周期性,导致压力波动,因此在设计两相流系统时必须考虑这种不稳定性.
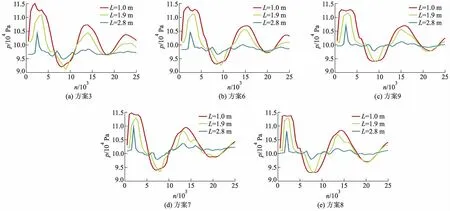
图6 不同方案下各测压点平均压力
2.5 气体对管道流体流速影响研究
将120 mm管道平均分为21层并进行各层混合流体的流速测量,所得各层平均流速如图7所示.可以明显看出,含气管道湍流速度分布不完全满足普朗特流速指数分布公式[15],但最大速度的位置保持不变,分别为3.82,4.89,6.03 m/s.相比于下半段管道,上半段管道由于存在体积更多的气体,平均液体速度向管道上部壁面急剧下降.认为相比于单相湍流,由于气泡的存在,气泡间的相互融合、分离,气体和水之间的相互作用会产生额外的湍流作用,从而使断面平均速度降低;相比于液相折算速度,气相折算速度较小,为满足流体的连续性,液相表现为更小的流速;逐渐向管道顶部移动的气泡群对液体流动产生除壁面之外的额外阻力[9].在流型转变时,靠近管顶的两相速度的差值较管底大;更大的气泡会使上、下壁面平均流速差值增多;jf越大,液体平均速度剖面图越对称.
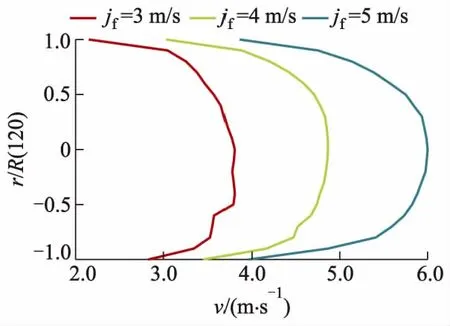
图7 液体流量对局部平均速度的影响曲线
3 讨 论
水平管道两相流在实际水利及农业工程应用中很常见,与垂直管道两相流相比,由于浮力的作用,不对称的气泡分布给水平两相流的试验和研究分析增加了复杂性.相邻气泡间、气液间、气壁间复杂的相互作用都会对整个流场的湍流结构产生影响.赵铎[16]首次运用Fluent进行二维单一管径下的VOF模型验证,通过改变气体流量和液体流量实现了流型的转变,但由于为考虑空气的压缩性导致有些模拟结果并不理想.张馨玉[14]用Fluent完成了管径对垂直上升管内气液两相流型的影响的模拟验证,通过不同管径模拟结果分析得出大管径下泡状流-塞状流转化过渡分界线都与气液两相流速呈正相关趋势,与文中得出的水平管流型转换结论一致.在水平两相流中,不同直径管道之间主要区别在于不同的流型转换条件,且管径大小差值越大,临界折算液体速度变化越大.文中运用三维VOF模型对不同管径下水平直管气液两相流进行了模拟分析,并认为较小的液相折算速度和管径时,由气团引起的压力波动随之变小,认为此时管道更为安全.
4 结 论
1) 三维Fluent模拟可以直观模拟瞬态过程中混合相的各相的运动情况及各相的存在形式,同时可得到各点的流速、压力等瞬时值、时均值等,且模拟结果可靠.
2) 随着液体流量的减小,产生泡状流到塞状流的过渡,此时浮力相对于紊流力对气泡的影响更强,气泡尺寸增大,气液两相之间的界面结构发生改变,产生更加清晰的分界面.
3) 管径越大时气泡更集中在管道顶部壁面且容易融合大气泡.jg=0.3 m/s时随着管道尺寸的增加,气泡流-塞状流过渡的起始点表现为更高的液相折算速度,从80 mm管道中的小于4 m/s转移到160 mm管道中的4 m/s.
4) 气液两相流压力波动存在周期性,随反应步数的增加,气液两相流动更加平稳,压力波动趋于平稳.且随着液相折算速度和管径的减小,压力波动减小,最大压差由9 439.2,12 826.5 Pa减小到9 136.0 Pa.
5) 最大速度位置满足单相湍流流速指数分布规律,相对于管道底部,顶部由于气泡作用使近壁面平均液体速度减小更多.

