宽垄沟灌土壤水分累积入渗特性试验研究及模拟

汪顺生，陈春来，王爱滨，傅渝亮*

(1. 华北水利水电大学水利学院，河南 郑州 450046； 2. 黄河水利科学研究院，河南 郑州 450003)

水是生命的源泉，是影响农业发展的先决性因素，是作物生长的基础，是生态环境的控制因素，具有不可替代性[1-2].作为中国第一用水大户，农业用水占用水总量的65%，而灌溉用水占农业用水90%以上[3-4].但是，中国灌溉水利用效率与发达国家水平(70%～80%)相比仍有很大的差距.因此，若要提高灌溉水利用系数，推进节水型农业的发展，创新和改进灌溉方式是一种有效可行的途径[5-6].目前，地面灌溉仍属全球应用最广、面积最大的灌溉方式.据第3次农业普查公报(第2部分)结果显示，中国灌溉耕地面积为6.189 0万hm2，其中喷滴灌等设施灌溉面积为1.001 8万hm2，占比16%，地面灌溉面积占比高达84%[7].

对于灌溉后土壤水分入渗特性，国内外专家进行了大量研究[8-10]； MOHAMMADZADEH-HABILI等[11]基于Green-Ampt模型提出了通过水分入渗试验数据对层状土水力参数进行估计的方法；LIPIEC等[12]研究了不同耕作制度条件下对土壤水分入渗的影响，结果表明常规耕作与减少耕作和免耕相比对土壤入渗能力和蓄水能力更优.聂卫波等[13]提出了沟灌累积入渗量简化计算方法，建立了忽略重力影响的理论系数与主要影响因素间的函数关系式，结果表明入渗水深对沟灌边界效应和拟合系数影响显著，沟底宽对沟灌边界效应和拟合系数影响较小，且拟合系数值可靠.马超等[14]通过室内试验研究了入渗水头对土壤水分运移的影响，结果表明相同入渗时间，累积入渗量随着入渗水头的增大而增大.王自奎等[15]利用土箱试验研究了垄沟灌溉土壤水分入渗特性，结果表明适当减小垄宽可以减少灌溉水的深层渗漏损失.

国内外学者就土壤容重、质地、土壤初始含水率等因素对沟灌土壤水分入渗的影响研究取得成果较多，对沟灌灌水沟特别是宽垄沟灌不同沟宽和沟深变化条件下的土壤水分入渗过程研究较少.基于此，文中在大田试验的基础上，结合软件和数值分析，对宽垄沟灌灌水后土壤累积入渗量进行研究，总结出宽垄沟灌土壤累积入渗量随时间变化规律，建立累积入渗量计算模型，为后续更多影响因素研究和灌区宽垄沟灌灌水技术提供科学依据.

1 试验与方法

1.1 模拟试验区概况

试验区为豫中地区华北水利水电大学农业高效用水实验场(113°48′E，34°50′N)，土壤质地为砂壤土，海拔110.4 m，北温带大陆性季风气候，多年平均降水量为637.1 mm，年平均气温14.5 ℃，日照时数为6.58 h，全年无霜期为220 d.表1为试验区土壤不同深度d的体积饱和含水率θs和干容重ρ.

表1 试验区土壤不同深度饱和含水量和干容重

1.2 试验及测定指标和方法

宽垄沟灌灌水试验在实验场裸土田间进行，灌溉水使用实验场地地下水.试验田经过整平、测量和设计，开沟起垄后，进行灌水沟尺寸校对.试验设置3种沟深、3种沟宽(沟宽均指沟顶宽)，共9个处理，各处理3次重复，同时设置沟宽55 cm、沟深27 cm的验证组.试验方案设计见表2，表中物理量分别为沟长ld、沟深H、沟宽D、沟底宽B、沟底纵坡f、垄宽L、单宽入沟流量Q.

土壤水分运动模拟：灌水沟横断面为对称梯形，取灌水沟半边为模拟区域.模拟根据试验不同处理组合尺寸进行，每个处理从沟首起每5 m取1个模拟断面.

灌水沟水深观测：灌水时利用控制阀与水表控制入沟流量，持续15 min，从沟首起5 m设标尺，灌水结束后，间隔一定时间读取标尺水面刻度.土壤含水量采用烘干法，每个模拟断面沟、坡、垄各取1个观测点，测定深度为5层1 m.

表2 土壤水分入渗试验方案设计

2 结果与分析

2.1 模型的建立和可靠性验证

土壤水分入渗过程用Hydrus软件进行模拟，忽略土壤温度等环境因素对试验的影响，试验模拟采用Van-Genuchten模型[16]，即

(1)

(2)

(3)

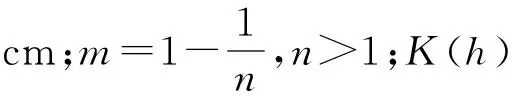
1) 初始条件为

θ(x,z,t)=θ0(x,z)，0≤x≤xB，0≤z≤zF，t=0，

(4)

式中：xB和zF为模拟区域边界在x和z方向的坐标；θ0(x,z)为体积初始含水率，cm3/cm3；t为水流最大消退持续时间，min.

图1 水分入渗试验模拟区域

2) 边界条件.宽垄沟灌灌水在田间进行，地表土壤干燥.为了便于计算，忽略地表的蒸发作用，将BF，FG，AG及BC视为零通量边界；AB视为自由通量边界；CD与DB为压力水头随时间变化的边界.边界条件具体为

BF边：

q/N=0，0≤t，

(5)

(6)

AG与BC边：

(7)

CD与DB边：

h(x,z,t)=h(t)，0≤t≤tmax，

(8)

式中：q为土壤水通量；N为土壤层数；tmax为水流最大消退结束时间，min.

利用Hydrus软件将试验所得土壤体积含水率进行反推得到土壤水分运动参数,见表3.利用验证组试验数据进行参数率定，结果如图2所示，图中θsm，θte分别为体积含水率的模拟值、实测值.实测值与模拟值拟合决定系数R2最小为0.731，证明选取参数是可靠的.

表3 土壤水力特性参数

为了验证模型精确度及是否适用试验组，将累积入渗量实测值与模拟值进行对比.取灌水沟为D=40 cm，H=20 cm处理，结果如图3所示，图中I为累积入渗量.可以看出，利用Hydrus模拟所得累积入渗量结果与试验值基本吻合，即Hydrus软件可以对宽垄沟灌灌水后土壤水分入渗过程进行模拟.

图2 土壤水分入渗参数适用性验证

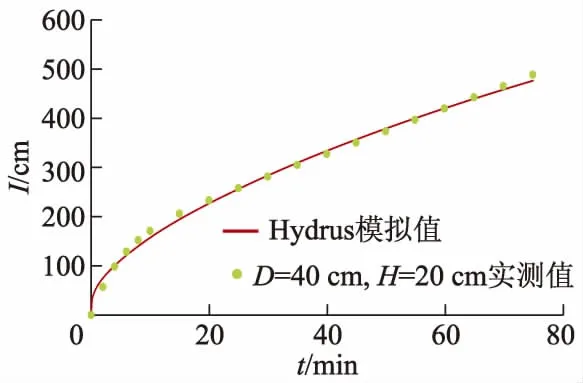
图3 D=40 cm，H=20 cm，累积入渗量实测值与模拟值对比

2.2 累积入渗量随时间变化规律

当L=110 cm，D=40 cm，H=20 cm时，距沟首15 m处沟中水深随时间变化如图4所示，横断面处的水流消退过程中以及相同条件下沟中水深变与不变累积入渗量随时间的变化关系如图5所示.

图4 灌水沟水深随时间变化关系

图5 沟中水深变与不变条件下累积入渗量随时间变化关系

对试验数据拟合后发现，水流消退过程中，沟中水深与时间为指数关系，即

(9)

式中：k为灌水结束时沟中水深，cm；g为经验参数.

由图5可知，无论沟中水深是否变化，累积入渗量随时间变化都经历快速增加阶段和稳定增加2个阶段.0～40 min时，累积入渗量随时间变化呈非线性增大关系；40～135 min时，定水头和变水头条件下累积入渗量随时间变化线性增大，但沟中水深不变时土壤水分入渗速率更快，并且随时间变化累积入渗量差值增大.这是由于水流消退前期累积入渗量受其影响存在延迟性；后期累积入渗量差值逐渐增大是因为随水流消退过程进行，灌水沟中水深降低，而灌水沟断面尺寸一定，沟中湿周减小，降低了水分侧向入渗速率.此外，水深降低造成沟底压力水头减小，降低了垂直方向水分入渗速率.

由分析结果可知，累积入渗量随时间变化经历了非线性递增和线性增加2个阶段.这是由于土壤未饱和时为非恒定入渗，饱和后处于稳定入渗状态.土壤非饱和时入渗状态可与电容充电模式比拟，因此采用电容充电模型[17-18]研究累积入渗量随时间变化规律，公式为

(10)

式中：W为电压值，V；tc为充电时间，min；E为电池充电的极限值，V；RC为电容与电阻的乘积.

图6为定水深与变水深条件下累积入渗量模拟值与实测值对比.由图可知，第1阶段非线性增加可表示为

(11)

第2阶段线性增加可表示为

I=ct.

(12)

将式(11)和式(12)相加得试验过程累积入渗量随时间变化函数关系式为

(13)

式(11)—(13)中：I为累积入渗量，a，b，c为经验参数.经分析，a为体积常数，b为时间常数，c为入渗第2阶段的水分入渗速率.

将大田所得定水深与变水深条件下累积入渗量随时间变化数据与式(13)计算所得数据进行对比，得实测值与计算值对比，如图6所示，可知实测值与计算值拟合较好，模型可以用于预测定水深与变水深条件下累积入渗量随时间变化规律.

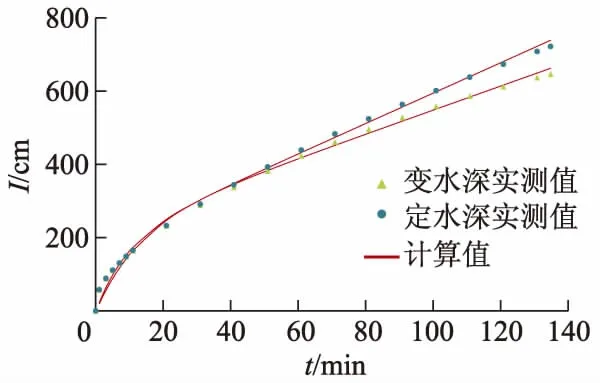
图6 定水深与变水深条件下累积入渗量计算值与实测值对比

将沟中水深随时间变化的函数关系式(9)变形得

(14)

对式(14)进行求导变形得

(15)

将式(14)代入式(15)得

(16)

(17)

式中：i为整个入渗阶段水分入渗速率，cm/min；其余参数为常数.

式(17)即为灌水沟中水深与水分入渗速率之间关系数学表达式.

2.3 沟宽对累积入渗量随时间变化规律的影响

沟宽变化条件下，L=110 cm，H=20 cm，距离沟首15 m灌水沟横断面处累积入渗量随时间变化关系如图7所示.

由图7可知，沟深一定，累积入渗量随时间变化表现为沟宽越大，累积入渗量越大：D为60和50 cm时较40 cm时I分别增加了21.88%和7.88%.这是由于沟深不变时，随灌水沟顶宽增大，灌水沟的边坡系数减小，灌水沟断面湿周增大，更有利于水分侧向入渗，增大了累积入渗量.

将图7中数据用式(13)进行拟合，得不同沟宽处理累积入渗量实测值与计算值对比如图8所示.由图可知，实测值与模拟值拟合较好，模型具有较高精确度.

图7 不同沟宽处理累积入渗量对比

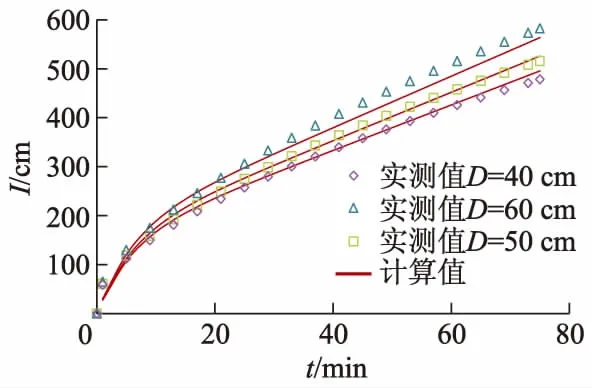
图8 不同沟宽处理累积入渗量实测值与计算值对比

2.4 沟深对累积入渗量随时间变化规律的影响

沟深变化条件下，L=110 cm，D=40 cm，距离沟首15 m处沟横断面处累积入渗量随时间变化关系如图9所示.

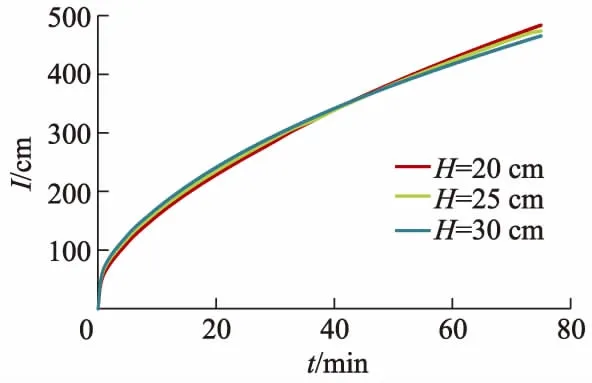
图9 不同沟深处理累积入渗量对比

由图9可知，当沟宽一定时，不同沟深处理条件下累积入渗量随时间变化关系大致可分为2个阶段，第1阶段为在40 min时间内，累积入渗量随灌水沟深度增大而增大；第2阶段为40 min后，累积入渗量随灌水沟深度增大而减小，H为30和25 cm时较20 cm时I分别减少了3.80%和2.05%.这主要是2种因素相互作用的结果，其一为灌水沟深度增大时水深也相应增大，灌水沟两侧承受的水压力增大，增大了累积入渗量；其二是当灌水沟宽度一定时，灌水沟深度越大湿周越小，降低了累积入渗量.

将图9中数据利用式(13)进行拟合，得实测值与计算值对比如图10所示.由图可知，实测值与模拟值拟合较好，模型具有较高精确度.

图10 不同沟深处理累积入渗量实测值与计算值对比

2.5 沟宽与沟深共同变化对累积入渗量的影响

利用式(13)对不同组合土壤水分累积入渗量的数据拟合得参数a，b，c值，并对结果进行方差分析，结果见表4.

表4 累积入渗量拟合参数

由表4可知，沟宽D和沟深H均对参数a和c具有统计学意义(P<0.01)，而对参数b不具有统计学意义(P>0.05)；交互项D×H对参数a，b，c不具有统计学意义(P>0.05).基于上述结果分析，仅利用Excel对表4中沟宽D与参数a和c，沟深H与参数a和c的数据之间关系进行拟合，得到参数a和c与沟宽D均呈线性增大关系，而参数a与沟深H呈线性增大关系、参数c与沟深H呈线性减小关系.

参数a和c与沟宽D的关系分别为

(18)

(19)

沟深与参数a和c的关系分别为

(20)

(21)

由表4分析结果可知，参数a和c受交互项D×H影响并不显著，利用Matlab软件对参数a和c与D和H进行拟合，得到参数a和c与D和H的关系分别为

a=1.73D+2.84H+31.43，R2=0.983，

(22)

c=0.031D-0.065H+4.714，R2=0.963.

(23)

将式(22)，(23)代入式(13)得

(0.031D-0.065H+4.714).

(24)

式(24)即为宽垄沟灌灌水后，水流消退过程中土壤水分累积入渗量随时间变化的函数关系.利用验证组测得数据与模型计算数据进行对比，结果如图11所示.由图可以看出试验观测值与模型计算值基本吻合，模型具有较高的计算精度.

图11 宽垄沟灌累积入渗量模型计算值与试验观测值对比

2.6 累积入渗量等值线分布

为了进一步研究不同沟宽与沟深条件下累积入渗量变化规律，利用Suffer软件模拟试验过程中累积入渗量随时间变化不同时刻等值线分布，如图12所示.

由图12可以发现，累积入渗量等值线随时间推移分布规律有很大变化.15 min时，无论沟宽或沟深增大，累积入渗量随之增大；35 min时，累积入渗量几乎不受沟深变化影响，而是随着沟宽增大而增大；55和75 min时，沟深变化开始对累积入渗量产生影响，即随着沟深增大，累积入渗量减小，沟宽对累积入渗量变化的影响规律不变，且当D=60 cm，H=20 cm时累积入渗量最大.

图12 不同试验组合条件下不同时刻累积入渗量等值线分布

3 讨 论

土壤水分入渗试验过程，由于累积入渗量随时间变化经历了非线性递增和线性增加2个阶段.在非线性增加阶段为非恒定流入渗，而电容充电未满之前为非恒定充电，可用电容充电状态比拟非恒定入渗状态，因此基于电容充电模型建立了累积入渗量随时间变化的函数关系，发现两者符合指数关系.将实测值与模拟值对比发现并无明显差距，表明模型具有较高的计算精度，所选模型参数适用.文中主要针对宽垄沟灌不同沟宽与沟深变化条件下的土壤水分入渗运动特性研究，所建模型参数可为以后进行更多因素分析提供基础，并在以后针对其他因素研究过程中对模型参数不断进行验证和优化，同时结果为灌区宽垄沟灌灌水技术提供科学依据.

4 结 论

1) 沟深一定条件下，随着沟宽增大，累积入渗量增大；沟宽一定条件下，随着沟深增大，累积入渗量减小.

2) 建立了累积入渗量随时间变化的函数关系，发现两者符合指数关系；建立了不同沟宽与沟深条件下的累积入渗量计算模型，并将模型计算值与试验观测值进行对比，发现两者之间吻合度较高，即模型可以比较准确预测不同沟宽与沟深条件下的累积入渗量值.

3) 累积入渗量等值线随时间推移分布规律有很大变化.在整个水流消退过程中，灌水沟顶宽增大时，累积入渗量也随之增大，而灌水沟深度对累积入渗量的影响分两个阶段.水流消退时间为15 min时，沟深增大则累积入渗量增大；35 min时，沟深变化对累积入渗量基本无影响；55和75 min时，沟深增大则累积入渗量减小.