多维建构 彰显数学思想
—— 以《三位数乘两位数》练习课为例
● 福建省福清市瑞亭小学 李 衡

《义务教育数学课程标准(2011年版)》把“双基”变为“四基”,即:基础知识、基本技能、基本思想、基本活动经验。基本思想在教学中有:数形结合思想、数学建模思想、符号化思想、转化思想等等。通过课堂实践活动的多维建构,彰显数学思想,能够让学生主动参与对知识的深入思考和加工中,从而内化成可以受用终生的思想。
《三位数乘两位数》是一节计算教学课,计算教学如何渗透数学思想,让学生形成运算能力,而不仅仅止步于计算技巧的熟练,是我们需要思考的问题。为了实现目标,本节课我没有放弃计算的基本技能,但更多的是进行数理相联、结构关联、直观演示的实践活动,其中渗透转化、类比、数形结合的思想。
一、数理相联,渗透转化思想
计算的学习源自生活,学生通过解决生活中的具体问题,把抽象的知识转化为具体的策略,在计算的过程中形成解决问题的策略意识。创设生活情境,不单单只是增强学生学习的兴趣。学习是一个认知的过程,也是一个情意过程,需要学生有学习的动力和欲望,通过生活情境的呈现,学生有了解决问题的需要,才能事半功倍地进入数学的思考过程。
四年级的学生已经学会了口算、估算、笔算三种计算方法,这三种计算方法的适用性是什么?如何在生活中自主选择运用合适的方法进行计算,这考查学生的计算能力和数学素养。因此,本节课我创设了购物猜价格的问题情境,出示三种书的单价分别是54元、109元、121元,对应的数量分别是24本、24本、43本,给出了四个总价:1296元、2616元、4783元、5203元,分别可能是哪本书的总价?这道题可以用到估算、笔算两种方法。而估算的运用不是简单地让学生把因数用四舍五入法看成整十整百的数来计算,而是要选择合适的方法进行判断。此时的方法就比较多样了。第一,看积的个位进行判断,两个因数个位相乘得到的结果的个位与积的个位是否一样,通过这种方法可以判断1296与2616是54×24与109×24的积,121×43的积可能是4783与5203中的一个。第二,看因数的大小判断积的大小,54×24的两个因数小于109×24,所以积也一定比它小,由此,学生可以得出1296是54×24的积,2616是109×24的积。第三,估成整十整百的数,121估成120,43估成40,120×40=4800,因为因数都估小了,所以积一定大于4800,那么4783就不是121×43的积。
知识只有应用了才能转化成能力,而学生只有在生活情境中通过解决问题,才能对知识进行运用,从而实现素养的转化。
二、结构关联,渗透类比思想
类比思想是根据知识的相似性,由此及彼产生的一种数学思想。数学的知识结构化在所有学科中尤为突出,知识之间联系紧密,方法也相通,所以才有了通一题会百题的说法。因此,数学的教学更关注的是知识的结构化,把所有相关的知识点联结起来形成一个体系,学生通过方法迁移把新知转化成旧知,在思考辨析的过程中,进行方法的拓展,完善知识结构,实现自我发展。
本节课教学三位数乘两位数,前期是两位数乘两位数,后续还可以拓展到多位数乘三位数,多位数乘四位数,这节课是这些知识承上启下的关键点,它们的算理和算法相同,知识结构是一样的。因此,教学这节课,我重在方法的比较迁移,通过比较迁移发现一般方法,从而总结出多位数乘法的计算方法。


第一轮比较的是两位数乘两位数和三位数乘两位数,如54×24和109×24都是把24分成20和4,先算4个54和4个109,再算20个54和20个109。由此发现,无论第一个因数是几位数,都是把第二个因数分解成几十和几,先算几个几,再算几十个几,所以第一个因数是两位数还是三位数都是一样的。
第二轮迁移,把三位数乘两位数的方法迁移到三位数乘三位数,第二个因数是三位数的时候,如168×124,怎么分呢?通过迁移得出124分成100+20+4,再与三位数乘两位数进行方法比较,发现方法是递进式的,本质是一样,都是分第二个因数,因数是两位数时,分成几个几和几十个几,拓展到因数是三位数时增加几百个几,顺着这个思路,学生很容易对方法进行拓展,第二个因数是四位数时,就增加几千个几,以此类推下去,几万个几……多位数乘法的知识结构形成了,学生对乘法计算的本质特征也就有了很好地理解。
还有一种关联是学习方法结构的关联,再以猜书本的价格为例,最后一本书,我设计了162×24,当学生一致认为只能通过笔算得出结果时,就引导学生观察,这个算式与前面的54×24、109×24、121×43这三个算式中的哪个算式有关联。通过观察能发现:54×24与109×24都与162×24有关联,都有一个因数24,其中54×24中的54的3倍是162,因此,本题不用列竖式计算162×24,只需要根据这种方法推理得出,用54×24的积1296×3就能算出162×24的积。
寻找关联形成结构,能够让数学的学习不再是碎片化,运用类比的思想能做到学一个知识,会一片知识,学生主动学习的积极性和解决问题的能力将得到很大的提升。
三、情理相融,渗透集合思想
集合就是把确定的、彼此可以区分的、具体的以及想象的对象看作是一个整体。集合思想是很重要的思想之一,现代数学的很多概念都是在它的基础上建立的,因此,小学数学中渗透集合思想显得尤为重要,它可以帮助学生深刻地理解知识,培养学生对事物进行辨析和归类的能力,有助于提高学生思维的条理性。
表示三位数乘两位数的积的范围时,我设计了在数轴上表示积的范围。首先出示一个开放式的算式: □□□× □□=?让学生猜测积是多少?学生得出的结果各不相同,有的开始猜测积的数量,认为积有无数个。教师接着追问:一直数都数不完吗?学生又产生质疑:似乎也不会数不完。数到哪里才到头呢?学生想到999×99,就是用最大三位数乘最大两位数得到的是最大的积。有了终点自然就想到了起点,那就是100×10,最小三位数乘最小两位数是最小的积,这样积的取值范围就找到了:大于1000小于98901,怎样才能直观地看到这些数呢?此时出示数轴,学生用大括号把1000和98901连接起来,三位数乘两位数的积就在这两个数之间,可能是四位数,也可能是五位数。
四、枚举验证,渗透数形结合思想
数形结合是将抽象的数学语言和直观的图形结合,既能借助数的精确性来阐述形的某些属性,又能借助形的直观性来阐述数量之间的关系。小学阶段,学生的形象思维占据主导,是形象思维向抽象思维过渡的重要阶段,数形结合符合小学生的思维方式,能有效地将数学思考过程直观化,从而帮助学生形成数学思维。
本节课在课后练习中有一道题是132×43和131×44,怎样快速地判断这两个积哪个比较大?这道题,学生通过观察发现,每道算式两个因数的和都是175,看第一个因数左边多了一个43,右边少了一个44,看第二个因数,左边少了一个132,右边多了一个131,这样对比下来,第二个算式的积比较大。但是这样的比较学生不容易理解,如果运用数形结合就会简单很多。可以让学生选择小点的数字,比较容易观察,学生选择了因数的和是10的算式,例如1×9、2×8、3×7 …… 9×1。用正方形来代替数据,1×9就是1个9相加,2×8是2个8相加,以此类推展示图形,学生逐次进行观察,例如1×9与2×8,少了一个9,但是却多了1个8……到了5×5达到最多,再往下又开始逐次减少。通过图形展示,很容易得出“两个因数和相同,因数之间的差越小,积越大”。
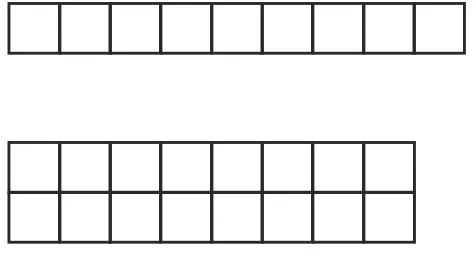


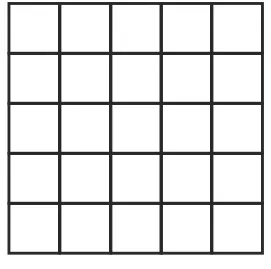
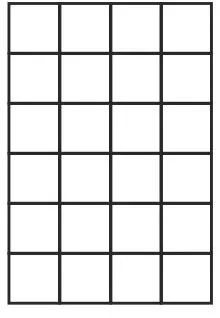
直观的图形把抽象的数据形象化,可以帮助学生更好地理解算式中的道理,直达数学的本质,提升了学生的学习能力。
数学的学习就是一个个实践活动过程的组成,这个活动需要学生主动参与,通过观察、操作、思辨、表达,把抽象的知识内化成素养,进而让数学的学科价值得以彰显。


