成长（增值）评估的具体操作研究

● 北京语言大学 谢小庆

进行成长评估，可以有两种思路：一是高起点、高水平，一步到位；二是低起点、低水平，第一步先“做起来”，第二步再力争逐步“做得好”。如有条件，当然可以选择第一种思路。本文介绍的“等值”和“残差”两种方法，属于第二种思路。

一、 从“达标（结果）评估”到“达标+成长（增值）评估”

2020年6月30日，由习近平总书记主持召开的中央全面深化改革委员会第十四次会议审议通过了《深化新时代教育评价改革总体方案》。10月13日，中共中央和国务院印发了这一总体方案。《深化新时代教育评价改革总体方案》的“总体要求”中提出：“改进结果评价，强化过程评价，探索增值评价，健全综合评价”。《深化新时代教育评价改革总体方案》已经为未来教育评价改革指明了方向，理清了思路。这就是：以“倡四评（结果、过程、增值、综合）”实现“破五唯（分数、升学、文凭、论文、帽子）”。未来，教育评价改革的一个重要思路就是，以成长（增值）评估来完善和补充原有的达标（结果）评估。

所谓成长评估模型是指一组定义、计算方法和规则，可以根据学生两个或多个时间点的表现，做出与学生、班级、教师和学校有关的解释。（王晓平，齐森，谢小庆《美国学校“成长测量”的7种主要方法》，2018年刊于《中国考试》第6期）进行成长评估，不仅可以更准确地了解学生实际的学习成效（outcome），同时还可以更准确、更清晰地了解教师、学校对学生成绩提高所产生的实际影响。

新的“达标+成长”的教育评估模型体现了一种新的教育理念。学习，不仅要追求“达标”，更要追求“成长”。对于一些基础好的学生，实现“达标”并不一定能够实现“成长”；对于一些基础薄弱的学生，即使暂时“达标”有困难，但仍然可以通过学习获得“成长”。

二、几个常用的成长评估模型

今天，在美国各州应用的成长测量模型主要有：基于纵向量表的增分模型（gain score）、轨道模型（trajectory）和分类模型（categorical）；基于回归方法的残差模型（the residual gain）、投射模型（projection）和学生成长百分等级模型（student growth percentile，简称SGP模型）；基于多变量分析的增值模型（value added）。

基于纵向量表的增分、轨道和分类等三种模型，目前在我国暂时不具有可行性，可以暂不考虑。今天，在美国应用最广泛的两个纵向量表是《智者平衡评估联盟测试系统（The Smarter Balanced Assessment Consortium, 简称SBAC）》（SBAC官网：http://www.smarterbalanced.org/）（维 基 百 科SBAC词 条：https://en.wikipedia.org/wiki/Smarter_Balanced_Assessment_Consortium）和《大学学习和就业准备联合测试》（Partnership for the Assessment of Readiness for College and Career，简 称PARCC）（PARCC官 网：https://parcc-assessment.org/）（维基百科PARCC词条：https://en.wikipedia.org/wiki/PARCC）。从2010年到2014年，SBAC和PARCC测试系统的开发分别获得了联邦政府1.78亿和1.86亿美元的资助。这仅仅是研发投入的一部分，此外，还有40多个州政府的投入，还有承担研发任务的培生等大公司的研发投入。目前，在我国尚难以进行这样规模的投入。

三、两种思路

进行成长评估，可以有两种思路：

1.高起点、高水平，一步到位；

2.低起点、低水平，第一步先“做起来”，第二步再力争逐步“做得好”。

有条件的时候，当然可以选择第一种思路。我这里介绍的“等值”和“残差”两种方法，属于第二种思路。

四、等值方法

为了对学生的成长进行评估，需要在特定时段（如一学期或一学年）的开始时和结束时，进行两次测试，即“入口”和“出口”的两次测试。由于练习效应，两次测试不能用同一张试卷。

尽管测试的编制者在命题过程中总是尽量保持难度的稳定性，但不同试卷之间在难度、分数分布方面的差别很难完全避免。两次测试的难度不同，分数的增长可能归因于学生的成长，也可能归因于试卷偏容易。如果第二次测试的分数提高明显，我们无法知道分数的提高是由于学生获得了“成长”，还是因为第二次测试的试卷比较容易。只有两次测试的成绩可以进行合理的转换，可以排除掉试卷难易度变化的影响，两次测试才具有可比性。

这样，就需要在不同难度的两份试卷之间建立可比性。这一建立可比性的过程，就是等值(equating)。

等值的具体做法是：首先编制试卷1和试卷2两份试卷。如果计划将试卷应用于对A校（或A学区、A地区）的学生进行成长评估，则将两份试卷在B校（或B学区、B地区）的一组学生中施测。根据施测结果，对两份试卷进行等值连接。之后，将试卷1作为A校的“入口”试卷，将试卷2作为A校的“出口”试卷。（见图一）

图一

在B校施测的方式可以有两种：第一种，上午测试一份试卷，下午测试一份试卷。这时，我们假设同一组学生在一天之内水平不会出现变化。第二种，将两份试卷合并为一份试卷，施测于B校的一组学生。（见图二）

图二

在试卷1与试卷2之间建立分数等值的方法是：

例如：

试卷1施测于B校的平均分=21.75。

试卷2施测于B校的平均分=19.25（试卷2比试卷1难一些）。

李萍的试卷2得分为27分。

李萍的试卷2相对于试卷1的等值分数=27+（21.75-19.25）

=27+2.5

=29.5

又如：

试卷1施测于B校的平均分=20.25。

试卷2施测于B校的平均分=22.55（试卷2比试卷1容易一些）。

李萍的试卷2得分为27分。

李萍的试卷2相对于试卷1的等值分数=27+（20.25-22.55）

=27-2.3

=25.7

成长分数的计算方法是：

例如：

李萍的试卷1（入口）得分26分。

李萍的试卷2（出口）卷面得分27分。

李萍的试卷2相对于试卷1的等值分数29.5分。

李萍的成长分数=29.5-26=3.5分（获得了成长）。

又如：

李萍的试卷1（入口）得分26分。

李萍的试卷2（出口）卷面得分27分。

李萍的试卷2相对于试卷1的等值分数25.7分。

李萍的成长分数=25.7-26=-0.3分（没有成长）。

以上介绍的是最简单、最粗糙的“平均数等值”方法。在有条件的学校（学区、地区），可以采用更精致的等值方法。在等值数据资料的收集方面，既可以采用以“人”为媒介的共同被试组设计，也可以采用以“题”为媒介的“锚测验”设计。在等值数据资料处理的数学模型方面，可以依据基于真分数假设之上的经典测验理论（classical testing theory，简称CTT），也可以依据基于潜在特质假设之上的题目反应理论（item response theory，简称IRT）。在两种理论模型的框架内，区别于数据收集的方式不同、所采用的计算方法不同等，又存在着多种不同的等值方法。（谢小庆《对15种测验等值方法的比较研究》 《HSK和MHK的等值》 《考试分数等值的新框架》分别于2000年、2005年、2008年刊于《心理学报》第2期 《考试研究》 第1期、 《考试研究》 第2期） （见图三）。

图三

五、残差方法

残差（the residual gain）方法也需要编制两套试卷，一套用于入口，一套用于出口。残差方法不需要对两套试卷进行等值连接。

残差方法所要回答的问题是：与根据入口成绩估计的预期出口成绩相比，某一学生的实际出口成绩如何？是高于预期成绩还是低于预期成绩，或者基本与期望成绩相一致。如果实际成绩明显高于预期成绩，我们就可以认为学生获得了成长。

残差方法所采用的是一种很容易理解的回归方法，基本计算方法是：在入口和出口成绩之间建立线性回归方程，根据回归方程和某同学的入口成绩，计算出该同学预期的出口成绩。之后，计算该同学预期出口成绩与实际出口成绩之间的“残差”。如果实际成绩高于预期成绩，该同学就取得了比较满意的“成长”；相反，则成长的情况不理想。

获得了一组学生（如一个年级的全体同学）的入口成绩（X）和出口成绩（Y）之后，很容易利用统计软件（如SPSS等）计算出回归系数，建立起回归方程。

例如：

Y=1.02X+1.2

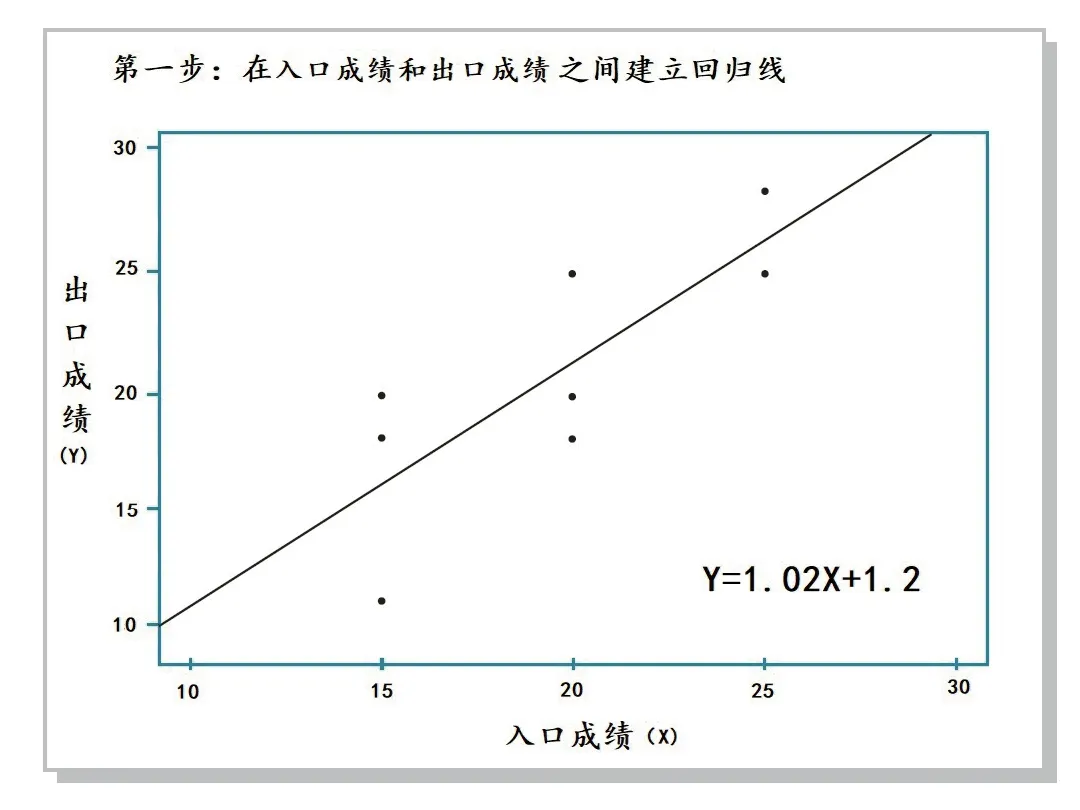
图四

根据一位同学的入口成绩和回归方程，很容易计算出其预期的出口成绩。

例如，李萍的入口成绩为20分，根据回归方程

Y=1.02X+1.2。

可以计算出：

李萍的预期出口成绩=1.02×20+1.2=21.6。

如果李萍的实际出口成绩是25分，那么李萍的成长分数

=残差

=实际出口成绩 – 预期出口成绩

=25-21.6

=3.4

图五

在残差方法中，包含着两个较强的假设：1.线性假设；

2.方差齐性假设。

在学生成长百分等级（SGP）方法中，不包含这两个假设，更为精致，是今天美国使用最广泛的一种成长评估模型，有20多个州使用，占所有使用成长模型的州一半以上。

SGP方法的计算较残差方法复杂一些，在有条件的时候，可以进一步采用更精致的SGP方法。（谢小庆《用于成长评估的学生成长百分等级模型：来自美国的经验》，2019年刊于《教育测量与评价》第6期；符华均等《基于学生成长百分等级模型的学业进步评价》。2019年刊于《中国考试》第2期；王帅鸣等《基于成长百分等级模型开展增值评价的实证研究》，2020年刊于《中国考试》第9期）

六、成长分数的应用

成长分数可以应用于学生、教师、学校（学区、地区）、学材、教法的评估。

学生：在向学生、家长报告“结果评估分数（达标成绩或期末成绩）”的时候，可以同时报告“成长分数”，可以使结果评估成绩处于高端、中断和低端的学生都能够受到激励、提醒和鼓励。

教师：计算和报告不同教师所教学生的平均成长分数，使任教于不同基础班级的教师，都可以看到自己在帮助学生获得成长方面所取得的实际效果。

学校（学区、地区）：计算和报告不同学校学生的平均成长分数，使学生基础不同的学校，都可以看到自己在帮助学生获得成长方面所取得的实际效果。

学材：计算和报告使用不同学材学生的平均成长分数，为不同学材的优劣比较，提供实证的参考依据。

教法：计算和报告采用不同教法学生的平均成长分数，为不同教法的优劣比较，提供实证的参考依据。