盲管段对原油管道顺序输送的影响因素分析与研究

杨军 孙艳 古丽努尔·牙哈甫 赵方强

1大庆油田设计院有限公司

2中国石油冀东油田勘察设计研究院

3新疆油田公司油气储运分公司

4青海油田格尔木炼油厂

随着油田开发进入中后期，开发的重点逐渐从整装油气田向边远小断块转移，为最大限度地降低运输成本，常将不同物性的原油采用顺序输送的方式进行储运[1]。但在顺序输送阶段，会产生一定的混油量，影响混油的因素有油品黏度、油品流速、输送顺序、输送距离、温度变化、地形起伏等，其中因沿途站场内工艺管道不可避免地存在旁通管汇，在替换油品的时候，这些位置的前行油品会混入主管中增大混油量，影响混油长度的计算[2-3]。加拿大至美国Keystone 管道的一个泵站有四根盲管，经实测，混油段长度较无盲管时增加了37.5%；赵海燕[4]利用Fluent 模拟了盲管对主管混油的影响，但计算模型中盲管长度较短，对主管的影响很小；GB 50235—2014《输油管道工程设计规范》中也指出设置副管后，在副管与主管交汇处会形成强烈的混油。目前，盲管段对主管混油的影响研究尚有不足，在此采用CFD方法[5]，结合多相流VOF和湍流RNGk-ε模型计算油品流速、主管管径、盲管长度等因素对混油段长度的影响，并对GB 50235—2014 中的混油段长度公式进行修正，以期为原油管道顺序输送安全运行提供理论依据和实际指导。

1 数值模拟方法

1.1 数学模型

基于VOF 模型对多相流问题进行求解[6]，在某个控制体S内，存在一种流体则体积分数判断为1，不存在则判断为0，如该空间内存在两种流体，则满足以下方程

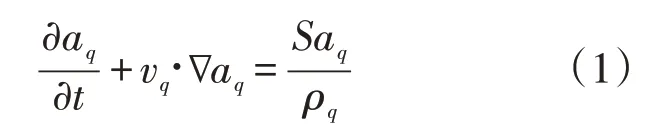
式中：aq为单元体积中第q相流体的体积分数，%；vq为第q相流体的流速，kg/s；ρq为第q相流体的质量，kg；Saq为控制体中第q相流体的体积分数，%。

计算中考虑重力因素影响

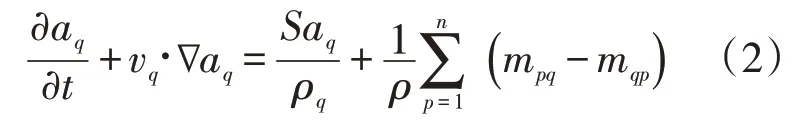
式中：mpq为第p相流体和第q相流之间的传质过程，kg；mqp为第q相流体和第p相流之间的传质过程，kg。

对于湍流求解问题，受涡旋黏性各向同性假设限制，采用对分离流、二次流、旋流等适应性较好的RNGk-ε模型进行求解。

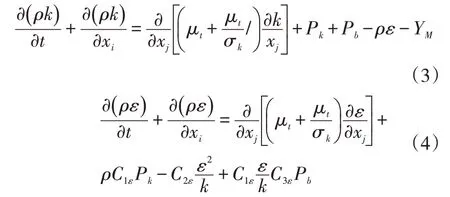
式中：ρ为各个节点的密度，kg/m3；k为湍动能，m2/s2；μt为湍动黏度，Pa·s；σk为由湍动能计算的普朗特常数，取1.0；xi和xj分别为第i个坐标和第j个坐标的方向；Pk、Pb分别为由速度梯度和浮力产生的湍流动能；ε为湍流耗散率，m2/s3；YM为扩散作用产生的波动；C1ε、C2ε、C3ε取值分别为1.44、1.92、0.09。

1.2 模型建立及网格划分

以某站场工艺管道为例，主管段管径508 mm，长度12 m，盲管段管径168 mm，长度2 m，盲管接口位于主管段4 m 处，设置6 个截面作为监测面，1号、2号、3号、4号截面分别位于主管段2、6、8和10 m处，5号、6号截面分别为主管段和盲管段沿流动方向对称剖面，7号截面位于盲管段1 m处（图1）。油品物性如表1所示，为了减少混油量和交替阶段雷诺数对混油的影响，采用黏度较大的1 号油品（后行油品）推黏度较小的2 号油品（前行油品），初始阶段主管段和盲管段内全为2 号油品。采用Workbench Mesh 进行非结构网格划分，由于混油尾部的形成受壁面黏性影响较大，计算y+作为第一层网格的高度，层数为8 层，生长因子1.1，对主管与盲管连接处进行网格加密，结果见图2。

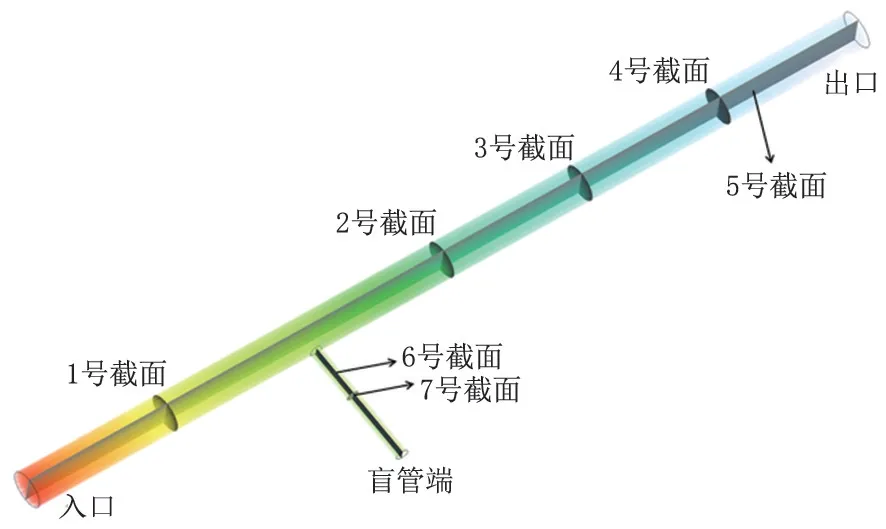
图1 模型及截面示意图Fig.1 Schematic diagram of model and setion

表1 油品物性参数Tab.1 Oil physical property parameters

图2 局部网格划分Fig.2 Local meshing division

1.3 求解方法

入口采用速度入口，出口采用压力出口，盲管闭端和管壁均为无滑移壁面。采用标准壁面函数对近壁面进行处理，PISO 求解瞬态问题，采用二阶迎风离散方法。考虑到动量方程中，压力梯度与两相表面张力之间的平衡，采用隐式体积力求解方式增加求解精度。迭代步长0.01 s，每一步的最大迭代次数为50，残差设定10-3。

2 结果与讨论

2.1 结果验证

在无盲管的情况下，5 s 时前行油品的体积分数随主管段轴线的变化趋势见图3。将混油段体积分数为1%～99%的长度定为混油长度，为6.7 m。将管径、油品物性和油品流速，代入一维扩散理论推导的计算公式中。

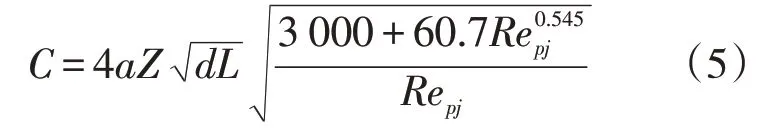
式中：C为混油长度，m；a为修正系数，无量纲；Z为综合变量，无量纲；d为管道直径，m；L为管道长度，m；Repj为混合黏度下计算得到的雷诺数，无量纲。

经计算，Repj=1.65×105，a=1.25，d=0.508 m，Z=1.645 m，L=12 m，得到混油长度C=7.1 m，比模拟运行结果偏大。这是由于一维模型假定混油浓度曲线为对称分布，忽略了混油径向扩散的影响，同时顺序输送过程中油品物性受到管道参数及温度、压力的影响，这些变化均会影响混油的浓度分布及混油段长度。相对误差5.63%，满足工程精度需求，说明采用数值模拟对顺序输送混油过程进行模拟是可行的。

2.2 混油机理分析

输油管道经济流速范围为1～2 m/s，在此取1.8 m/s，得到不同时间下6号截面的混油浓度分布（图4）。由于两种油品密度和黏度的差异，后行油品在t=5 s 时进入盲管段，此时后行油品在主管中已行进9 m，越过了盲管段。这是由于流经盲管时，贴近壁面处会形成涡流区主管具有一定的携带作用，偏流作用减弱。在t=17 s时，后行油品第一次到达盲管闭端，t=35 s时，后行油品由盲管闭端返回接口处，此时由于重力作用两种油品在接口处形成封闭交换流，混油机理为对流传递作用，流体特征高度接近管径的一半；35 s后，混油机理为湍流扩散作用，前行油品在盲管中被逐渐替换，这一时间远大于对流传递所需要的时间。图5 为7 号截面前行油品体积分数随时间的变化曲线，在t=5 s时，前行油品的体积分数开始下降，在35 s 之前，体积分数下降较快，35 s 之后，体积分数下降缓慢，曲线斜率变缓且较之前更加平稳，表明混油机理了发生改变，与图4的浓度分布一致。

图3 5 s时主管轴线上的前行油品体积分数Fig.3 Forward oil volume fraction on the main axis at 5 s

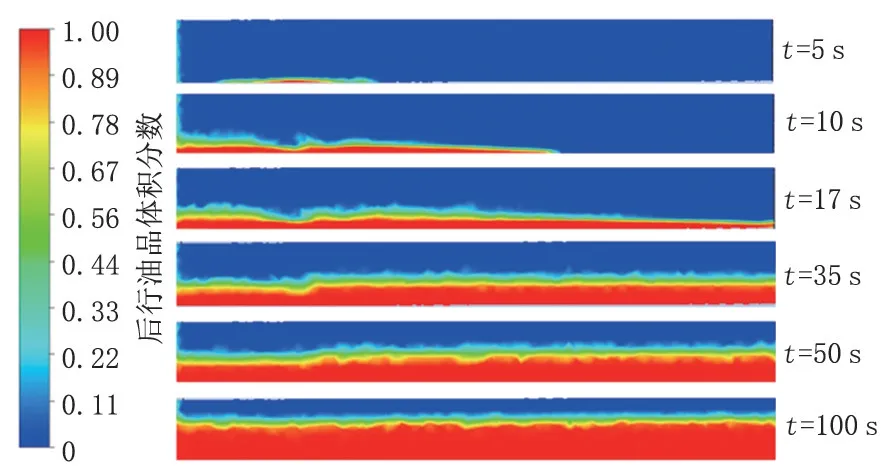
图4 不同时间盲管段混油浓度分布Fig.4 Mixed oil concentration distribution in blind pipe section at different time

图5 7号截面前行油品体积分数变化Fig.5 Forward oil volume fraction change of Section 7

不同时间下5 号截面的混油浓度分布（图6）。两种油品在交界处出现了明显的分层现象，径向浓度分布不一致，后行油品的混油头以楔形方式从管道下方混入前行油品，随着时间的延长，混油段长度逐渐增加，两种油品的接触区域不断变大。在经过盲管后，由于主管流速较大（1.8 m/s），盲管流速较小（对流传递阶段为0.12 m/s，湍流扩散阶段速度更小），沿着盲管接口处会形成较长的混油拖尾。在主管段中，油品受湍流扩散、重力及浮力的影响，重力作用使混油段更长，浮力作用使拖尾分割成多个独立的混油段（图7）。

图6 不同时间下5号截面的混油浓度分布Fig.6 Mixed oil concentration distribution of Section 5 at different time

图7 50 s时后行油品的体积分数Fig.7 Trailing oil volume fraction at 50 s

2.3 流速对混油的影响

输油管道的输量会根据实际工况发生改变，导致油品流速不一致，对不同流速下3号截面前行油品的体积分数进行统计（图8）。主管段混油变化分为三个阶段：第一阶段，后行油品还未到达截面位置，前行油品的体积分数为1，当流速为0.5 m/s和2 m/s时，此阶段的持续时间分别为4 s和2 s；第二阶段，前行油品体积分数呈直线下降，曲线斜率较大，且流速越大曲线斜率越大，当流速为0.5 m/s和2 m/s 时，此阶段前行油品体积分数分别下降到38%和4%；第三阶段，前行油品体积分数呈缓慢下降，曲线斜率较小，且流速越大曲线斜率越小。因此，流速越大，雷诺数越大，油品的替换速度越快，后行油品对管壁残留混油的携带冲刷作用越强，产生的混油量和拖尾越少，混油段长度越短。

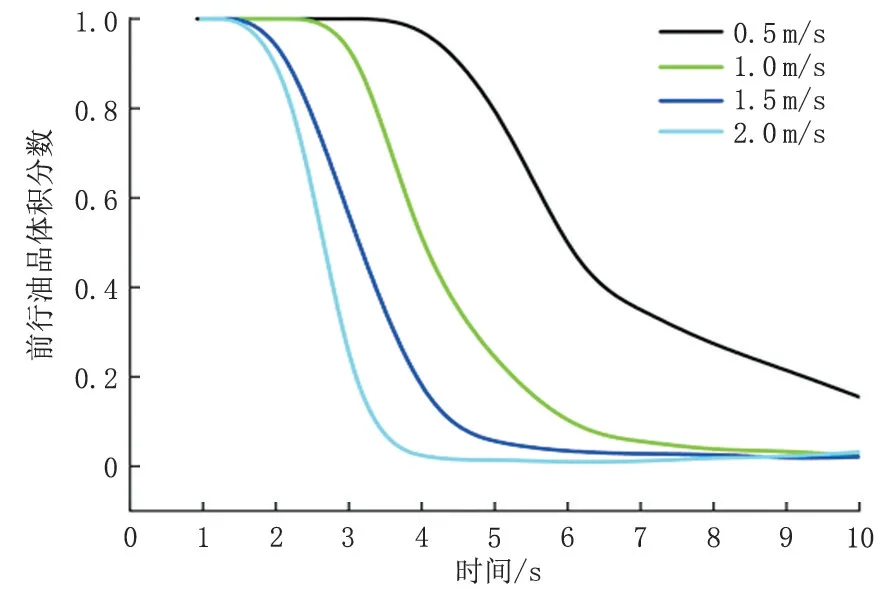
图8 3号截面前行油品体积分数变化Fig.8 Forward oil volume fraction change of Section 3

流速不仅会影响主管段的混油量，也会对盲管段的油品替换速度和拖尾长度产生影响，图9 为7号截面在不同流速下的混油浓度分布（50 s）。随着流速的增加，在相同时间内，盲管中后行油品的体积分数越来越小，前行油品的体积分数越来越大，说明油品替换速度越来越慢，与主管段的混油变化相反。这是由于在盲管与主管连接截面不变的情况下，尽管单位流量的油品携带能力没有变化，但因流速的增加，携带前行油品的时间变少，与盲管段进行湍流扩散的时间减少，油品替换速度减慢。

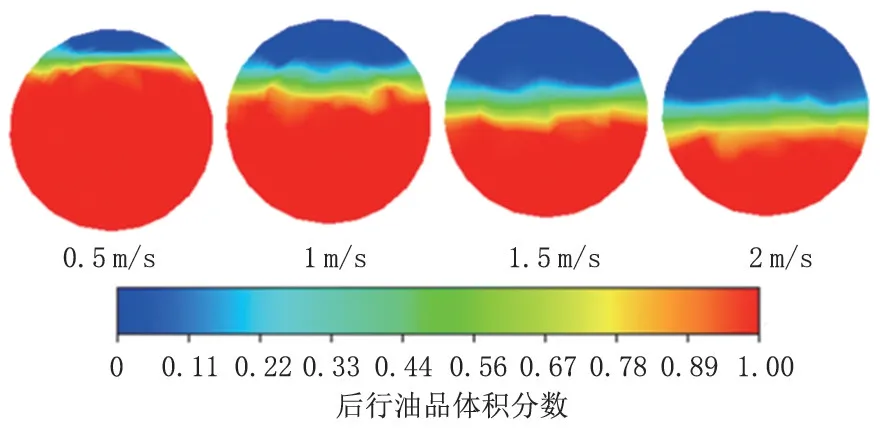
图9 7号截面在不同流速下的混油浓度分布（50 s）Fig.9 Mixed oil concentration distribution of Section 7 at different flow rates（50 s）

将盲管中前行油品的体积分数小于1%视为置换合格，对流速和油品替换时间进行敏感性分析，结果见图10。当流速超过1.5 m/s 时，盲管中油品替换速度大幅减小，替换时间大幅增加，在主管中会形成很长的混油段和拖尾。

2.4 主管直径对混油的影响

在油气站场中，较多使用DN400～500 mm 管道，对应管道直径分别为0.406 m、0.457 m 和0.508 m，流速为1.5 m/s，模拟主管管径变化对7号截面前行油品体积分数的影响，结果见图11。主管管径越大，混油在径向方向上的速度越大，前行油品体积分数下降得越快，但对盲管段油品替换速度的影响有限。

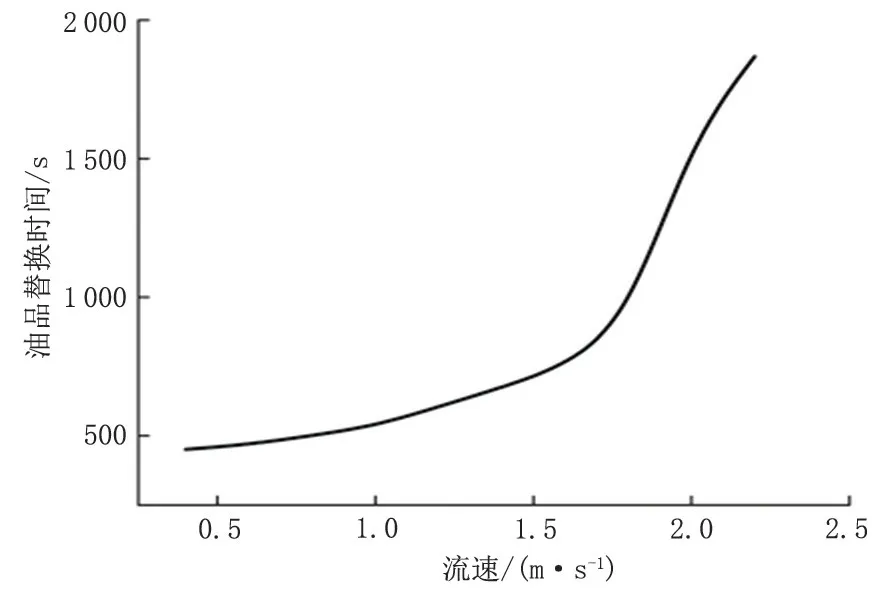
图10 流速与油品替换时间的关系Fig.10 Relationship between flow rate and oil replacement time

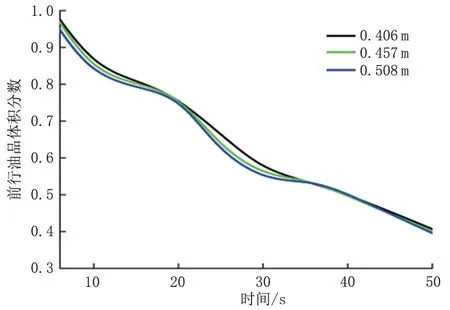
图11 7号截面前行油品体积分数变化Fig.11 Forward oil volume fraction change of Section 7

2.5 盲管长度对混油的影响

在旁通管路中设置单流阀，单流阀与主管之间的距离则为盲管段长度，设计中通常取1～10 倍的主管直径长度，流速为1.5 m/s，盲管中前行油品的体积分数小于1%视为置换合格，敏感性分析见图12。当盲管超过4倍的主管管径时，油品替换时间大幅增加，通过统计，后行油品第一次到达盲管闭端的时间见表2。从表2 可以看出，对流传递阶段的流速均为0.13～0.16 m/s，变化不大，但后行油品替换盲管前行油品的时间却不断增加，说明盲管长度超过4d时，涡流区顶部的速度分量沿轴向和径向方向分解，使涡流区不断扩大，湍流扩散作用对油品替换的影响减弱，此时越靠近盲管闭端前行油品越难与后行油品发生湍流扩散。

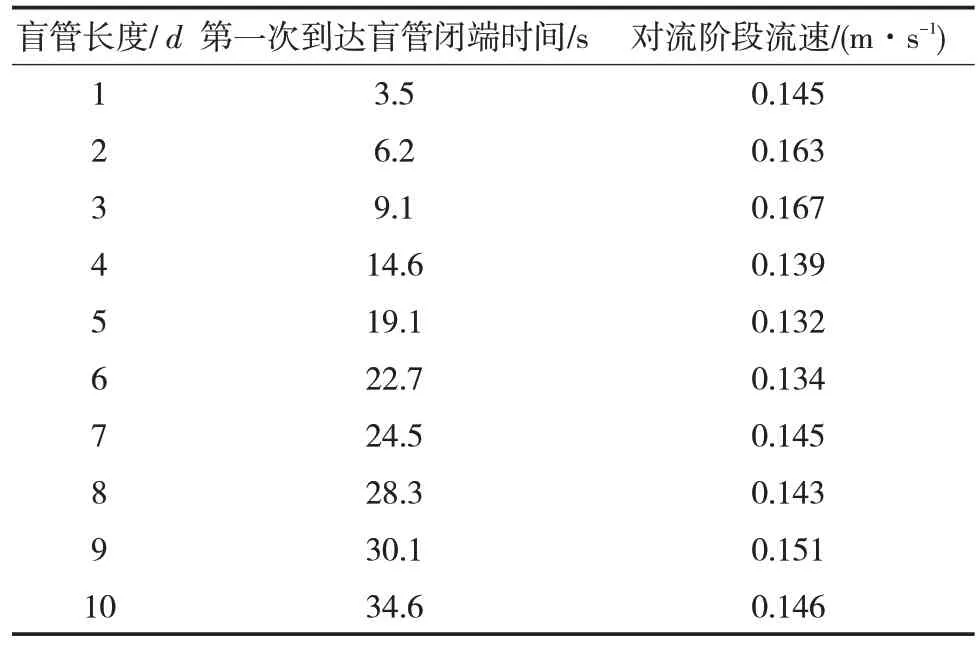
表2 后行油品第一次到达盲管闭端的时间Tab.2 First time of trailing oil reaches the closed end of the blind pipe

2.6 数据拟合

根据上述模拟，流速和盲管长度对混油长度的计算影响较大，主管直径对混油长度的计算影响有限，图10、图12 曲线均呈幂指数分布。在此，考虑量纲的和谐性，结合量纲齐次定理，确定函数关系式为

式中：T为油品替换时间，s；v为油品流速，m/s；d为主管管径，m；A、B、C分别为拟合参数。

采用Origin 软件对替换时间、盲管长度、流速进行多元非线性拟合，拟合后的三维曲面见图13，相关系数R2=0.979 6，说明拟合程度较好，相关公式为

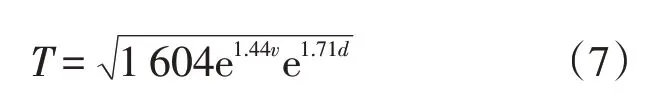
根据油品替换时间与流速可计算真实混油长度。GB50235—2014《输油管道工程设规范》中采用了Austin的经验公式计算混油长度，但条文说明也提到该公式没有考虑分输或管径变化引起的混油量。虽然在盲管段中的油品替换时间较长，但根据图8 结果，除低流速（0.5 m/s）外，其余流速下主管中前行油品的体积分数在9 s后均小于1%，即9 s后虽然盲管中还有前行油品不断流出，但对于混油切割及油品质量的影响可忽略[7-9]。

因此，对Austin的经验公式进行修正，当混油雷诺数Re大于临界雷诺数Relj时

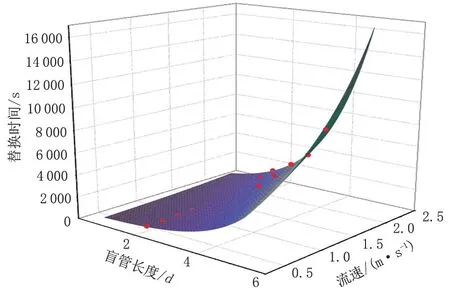
图13 拟合后的三维曲面Fig.13 3D curved surface figure after fitting

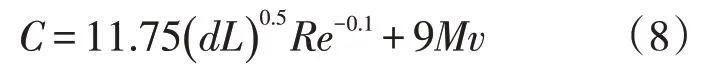
当混油雷诺数Re小于临界雷诺数Relj时

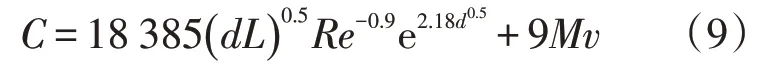
式中：C为混油长度，m；d为管道直径，m；L为管道长度，m；Re为混油雷诺数，无量纲；v为油品流速，m/s；M为盲管数量。

3 结论

（1）采用CFD 的方式对原油顺序输送进行了数值模拟，盲管段的混油机理为对流传递和湍流扩散作用，其中前者作用时间较短，流体特征高度接近管径的一半；后者作用时间较长，在主管中形成较长的混油拖尾。

（2）流速和盲管长度对混油长度的计算影响较大，主管直径对混油长度的影响有限。

（3）流速越大，主管段中油品的替换速度越快，混油量越少，盲管段与主管段的混油变化相反。为减少盲管段对混油的影响，流速不应超过1.5 m/s，盲管长度不应超过主管直径的4倍。