天然气携砂在90°弯管中的冲蚀磨损数值分析
史晶莹 陈燕才 蔡晓明 高翔 徐恒元 梁昌晶
1大庆油田设计院有限公司
2河北华北石油工程建设有限公司
3渤海钻探第四钻井工程分公司
4河北华北石油港华勘察规划设计有限公司
随着油气田的深入开发,气藏的出砂量越来越大,高压高流速的天然气携带固体颗粒以固定的冲击角度不断磨损管道内壁、阀门和弯头等部件,长时间的冲刷腐蚀会对管道造成侵蚀或刻蚀破坏,其中弯头因涉及到二次流问题,冲蚀磨损最为严重[1]。因此,研究不同流动参数对弯管的冲蚀规律及固体颗粒的运动轨迹对于预防输气管道携砂冲蚀具有重要意义[2-3]。
国内外诸多学者采用旋转圆柱电极、管流试验装置以及喷射试验装置进行了冲蚀磨损试验,并根据试验结果总结了大量的冲蚀模型[4-8],但试验的可重复性不高,且试验设计具有盲目性,因此目前多采用Fluent、Comsol 等流体力学软件进行冲蚀数值模拟。张孟昀等[9]通过加入DPM离散相模型,研究了相同条件下盲管与弯管的流场分布与冲蚀情况,发现弯管的耐蚀性远小于盲管;李沧等[10]采用Fluent 软件对输气管道气-固两相流进行了模拟计算,发现最大冲蚀速率随入口流速和固体颗粒质量流量呈正比关系;曹学文等[11]分别研究了砂粒参数、流动参数对冲蚀速率的影响,发现流速与冲蚀速率呈正相关,出口压力变化对冲蚀范围及冲蚀速率影响不大;YAP Y J[12]采用计算流体力学软件研究了颗粒直径、管径比对弯管的冲蚀影响,得到管径比的增加会减小冲蚀区域的结论。以上研究对弯管冲蚀规律的研究具有重要意义,但均基于特定工况且采用单一变量控制法,对不同流动参数之间的变化规律认识不足,且未见对最大冲蚀位置的预测和不同重力方向对冲蚀的影响。因此,采用Fluent软件进行气-固双相耦合,选用E/CRC 冲蚀模型对固体颗粒的流场分布、冲蚀速率及冲蚀位置进行模拟,以期为管道的冲蚀预测提供理论依据和实际参考。
1 理论模型
1.1 连续相方程
甲烷作为连续相,在Eulerian 坐标系下求解N-S方程得到流场分布,其中连续性方程和动量方程为
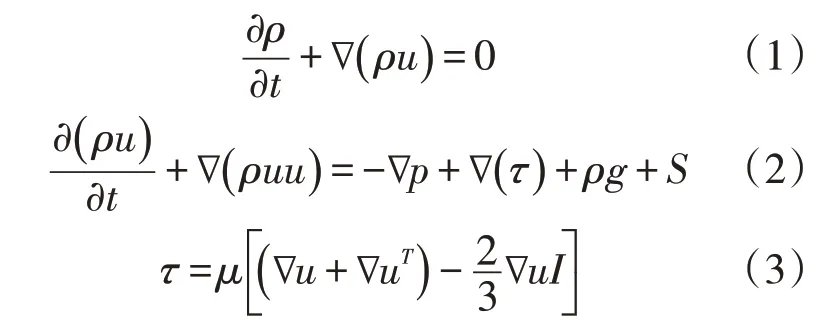
式中:u为流体流速,为x、y、z三个方向的分量,m/s;ρ为甲烷密度,kg/m3;t为运行时间,s;p为压力,Pa;τ为应力张量;g为重力加速度,m/s2;μ为甲烷黏度,Pa·s;S为离散相相对于连续相的附加源相;I为单位张量。
1.2 离散相方程
固体颗粒作为离散相,在Lagrangian 坐标系下通过牛顿第二定律确定颗粒的运动轨迹,公式为
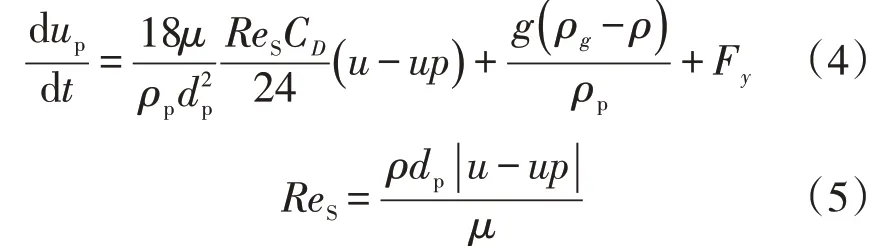
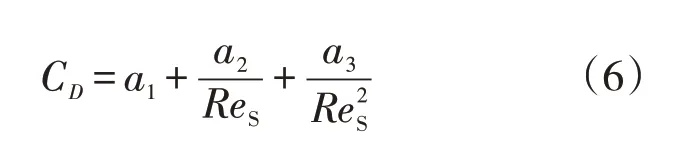
式中:up为固体颗粒速度,m/s;ReS为相对雷诺数;ρp为颗粒密度,kg/m3;dp为颗粒直径,m;CD为曳力系数;Fy为y轴方向其他的作用力;a1、a2、a3为离子光滑常数,可参考文献[13]。
1.3 冲蚀模型
Fluent 中内置了多种经验及半经验的冲蚀模型,其中E/CRC模型计算二次流弯管壁厚减薄的精度较高,且该模型充分考虑了冲击角度、材料粗糙化对壁面的影响,因此采用该模型计算冲蚀速率,公式为
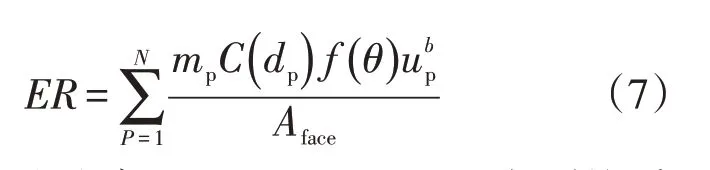
式中:ER为冲蚀速率,kg/(m2·s);mp为颗粒质量,kg;C(dp)为粒径函数,取1.8×10-9;b为速度指数,取2.6;Aface为壁面面积,m2;f()θ为冲击角函数,采用分段线性的方式进行定义,在冲击角0°、20°、30°、45°、90°时的函数值分别为0、0.8、1、0.5、0.4。
1.4 壁面回弹模型
固体颗粒在与壁面撞击过程中会有能量损失和传递,反弹速度会小于冲击速度,因此通过建立回弹模型预测动量变化趋势,采用恢复系数表征固体颗粒在碰撞前后动量的变化。输气管道大多为碳钢管线,Forder等[14]利用铁介质建立的回弹模型公式为
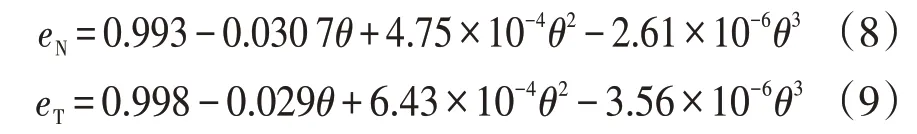
式中:eN和eT分别为法向恢复系数和切向恢复系数。
2 数值模型
2.1 弯管模型
弯管模型直径D=60 mm,为了避免回流对精度的影响,水平和竖直管段长度均为10D=600 mm,曲率半径为1.5D=90 mm(图1)。
2.2 网格无关性分析
网格质量和数量直接影响模拟计算的精度和速度,在流速6 m/s、颗粒直径100 μm、颗粒质量流量0.2 kg/s 的条件下,对不同网格数量下的冲蚀速率进行适用性分析(图2)。当网格数量小于1 002 567 时,冲蚀速率呈无规律上下波动趋势,当网格数量大于1 662 882 时,冲蚀速率基本保持稳定,因此在保证计算精度的前提下,选用网格数量为1 662 882。对入口和出口壁面进行膨胀层设计,划分5 层,生长因子1.2,同时对弯曲部位进行网格加密(图3)。

图1 弯管示意图(流动方式1)Fig.1 Schematic diagram of elbow(flow mode 1)
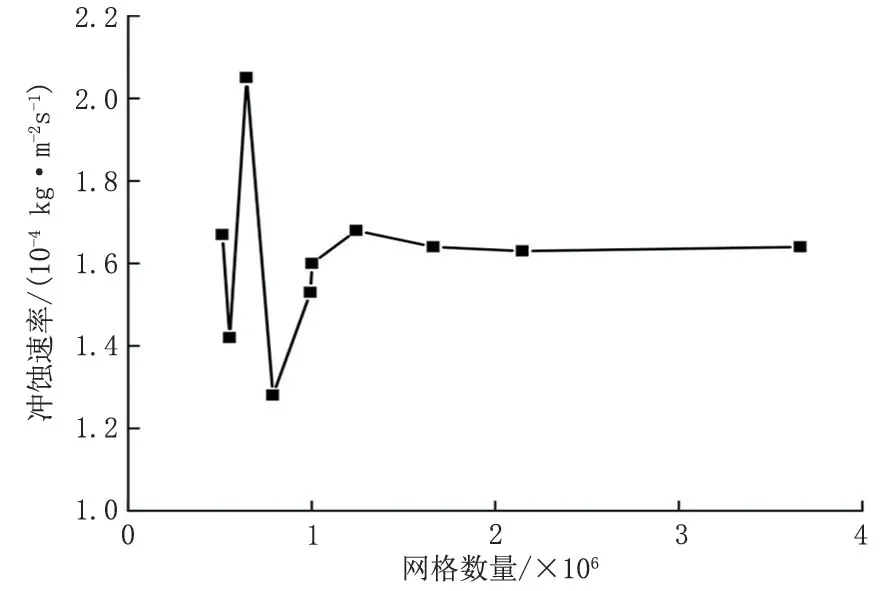
图2 网格无关性分析Fig.2 Grid independence analysis
2.3 边界条件和求解方式
对固体颗粒属性进行简化处理,假设颗粒为密度均匀的球形,且在射入后无旋转运动,同时忽略颗粒受到的虚拟质量力、压力梯度力和升力等。模型及边界条件设定见表1。入口及出口的湍流强度和水力半径分别为5%和60 mm,常温常压下甲烷密度0.668 kg/m3,固体颗粒密度2 650 kg/m3。

图3 弯头处的网格划分Fig.3 Mesh division at the elbow

表1 模型及边界条件设定Tab.1 Model and boundary condition setting
选用压力-速度稳态求解器对边界条件进行求解,利用SIMPLE 算法,为了得到较好的收敛效果,压力、动量、湍动能采用二阶迎风算法,设置监视器中残差范围为10-5。
3 结果与讨论
3.1 流场分布
在流速4 m/s,颗粒直径100 μm,颗粒质量流量0.6 kg/s 的条件下,弯管的轴向截面分布云图见图4。水平管道的压力和速度分布基本稳定,受流体黏滞力的影响,速度在近壁面处的数值较小,流体经过弯头时固体颗粒发生直接碰撞并反弹,二次流、速度场和压力场发生变化。其中压力较大处出现在弯管外侧,此时流体在弯管处产生离心力,对弯管内侧的牵引作用使流动方向发生改变,内侧出现负压,从内侧到外侧压力值呈递增趋势,内侧的压力转化为动能;速度较大处出现在弯管内侧,因此颗粒在弯管外侧和竖直管道内发生碰撞和滑动,故只有弯管外侧和沿竖直管道方向发生冲蚀,内侧不发生冲蚀。
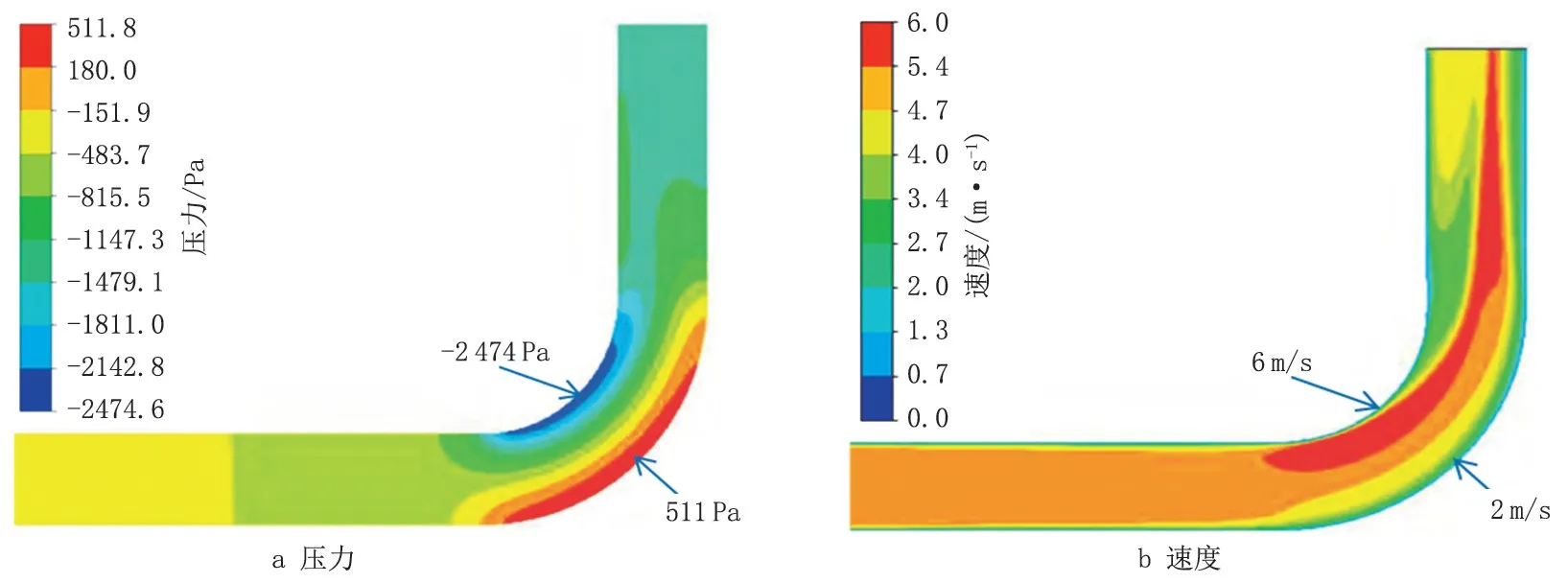
图4 轴向截面分布云图Fig.4 Distribution cloud map of axial section
3.2 流速对冲蚀的影响
在颗粒直径100 μm,颗粒质量流量分别为0.2、0.4、0.6、0.8、1.0 kg/s 的条件下,对不同流速下的冲蚀速率进行模拟,结果见图5。在颗粒质量流量一定的条件下,冲蚀速率随流速的增大而增大,且在小于4 m/s 时,质量流量的变化对冲蚀速率影响不大,而大于4 m/s 时,冲蚀速率提升较快,故4 m/s 为临界流速,在实际生产中尤其是颗粒质量流量较大时应避免超过此流速。在颗粒质量流量较小时,冲蚀速率随流速呈线性变化,此时流体所携带的颗粒数量有限,即使初始动能较大,对管壁的损伤依然有限;在颗粒质量流量较大时,颗粒与壁面之间碰撞的概率变大,冲蚀速率随流速呈指数变化。

图5 流速对冲蚀的影响Fig.5 Effect of velocity on erosion
颗粒质量流量0.6 kg/s 的条件下,流速2、6 和10 m/s 的冲蚀云图见图6。在低速情况下,颗粒动能较小,形成的冲蚀区域较小且集中在水平管段底部,随着流速的增大,连续相对离散相的作用力增加导致颗粒的动能增大,冲蚀区域变大且逐渐向竖直管线两侧扩展。其中流速为2、4、6、8、10 m/s 时的最大冲蚀角度分别为18°、32°、43°、51°、55°,颗粒与管道壁从直接碰撞转为滑动碰撞,二次碰撞的区域变大,与图6云图中的高亮冲蚀区域相符。

图6 不同流速下的冲蚀云图Fig.6 Erosion cloud map at different flow rates
3.3 颗粒直径对冲蚀的影响
在流速6 m/s,颗粒质量流量分别为0.2、0.4、0.6、0.8、1.0 kg/s的条件下,对不同颗粒直径的冲蚀速率进行模拟,结果见图7。在颗粒质量流量一定的条件下,随颗粒直径增大,冲蚀速率先增大,在颗粒直径超过100 μm 后,逐渐呈平稳趋势。这是由于气-固两相耦合作用时,小颗粒与壁面之间的碰撞更充分,而大颗粒转移到气体中的动能更多,流体的携带能力下降,颗粒之间的有效碰撞增多,大颗粒与壁面之间的碰撞机会和强度均减少,同时大颗粒因重力造成的停滞作用对后续颗粒的冲蚀影响较大,因此冲蚀速率保持平稳。
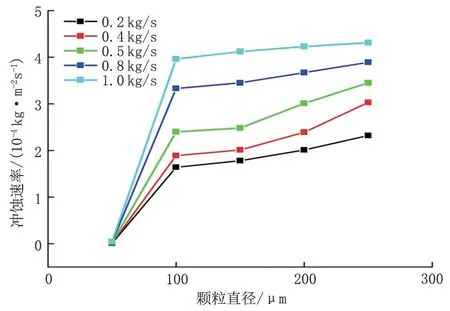
图7 颗粒直径对冲蚀的影响Fig.7 Effect of particle diameter on erosion
在颗粒质量流量0.6 kg/s 的条件下,随着颗粒直径的增大,最大冲蚀速率和冲蚀面积均有所增加,但最大冲蚀位置基本不变。其中颗粒直径为50、100、150、200、250 μm 时的最大冲蚀角度分别为47°、46°、46°、45°、45°,均在45°~47°之间,由于曳力作用使小颗粒的碰撞角增大,导致大颗粒的最大冲蚀角度略小于小颗粒,但总体上颗粒直径对最大冲蚀位置的影响不大。图8为颗粒直径50、150、250 μm的冲蚀云图。

图8 不同颗粒直径下的冲蚀云图Fig.8 Erosion cloud map of different particle diameters
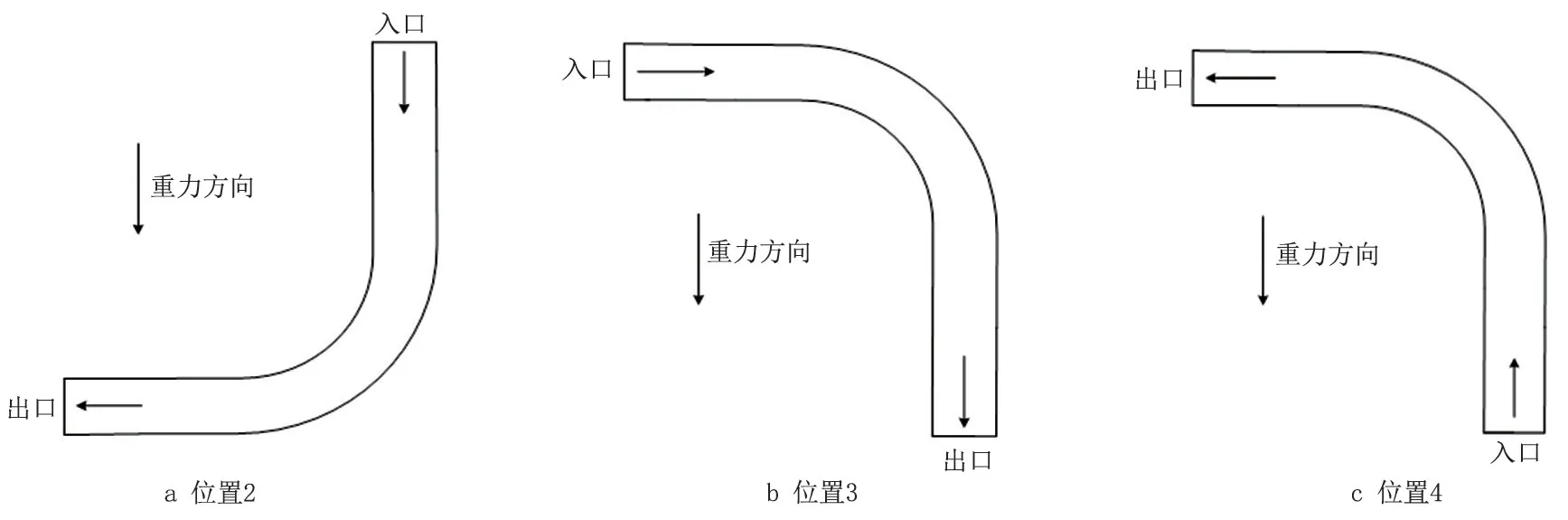
图9 不同流动方式示意图Fig.9 Diagram of different flow modes
3.4 重力方向对冲蚀的影响
在实际工况中,管道的布置形式及重力场的方向直接影响冲蚀区域。分别对4种重力场的的弯管冲蚀进行模拟,其中一种携砂气体流动方式如图1所示,定义为流动方式1,其余3 种携砂气体流动方式见图9。

图10 不同位置的冲蚀云图Fig.10 Erosion cloud maps at different locations
在流动方式1 和流动方式4 中,重力对颗粒运动起减速作用;流动方式2 和流动方式3 中,重力对颗粒运动起加速作用,冲蚀云图见图10。流动方式2 和流动方式3 对弯管的冲蚀程度远大于流动方式1 和4,其中流动方式4 受到的冲蚀磨损最轻微。位置3流体携带颗粒撞击弯管后,由于重力作用,势能增大,二次流能量较大;流动方式2流体先沿重力方向竖直向下运动,势能较大,撞击弯管后将损失一部分能量,故二次流能量减小;流动方式1流体在撞击弯管后为克服重力作用,二次流能量更小;流动方式4流体需先克服重力作用,然后再撞击弯管,二次流能量最小。因此,当入口或出口方向与重力方向起正向叠加作用时,冲蚀较严重,冲蚀严重程度由大到小依次为流动方式3、流动方式2、流动方式1、流动方式4。
重力场的方向不仅会影响最大冲蚀速率,也会影响冲蚀区域。对比流动方式1 和流动方式3,在入口水平流动的过程中,由于重力作用,在靠近弯头入口区域的管道下方存在一定的轻微磨损,但迎角较小,主要以切削作用为主;流动方式1在进入弯头区域后立刻造成了较大的冲蚀,而流动方式3在进入弯头区域的后方才造成较大冲蚀,这与重力方向带来的颗粒偏流有关,且颗粒的动能越大,差异越明显。对比流动方式2 和流动方式4,在入口竖直流动的过程中,无论重力与弯管布置方向的关系以及携砂天然气的流动方向如何,因无偏流,入口直管段几乎没有冲蚀损伤,但流动方式2与重力方向相同,因此在进入弯头区域后立刻造成了较大的冲蚀,冲蚀区域集中在弯头及出口管道上。
4 结论
通过对弯管内携砂气体流速、颗粒质量流量、颗粒直径等进行模拟分析,发现颗粒质量流量较小时,冲蚀速率随流速呈线性变化且变化幅度不大,颗粒质量流量较大时,冲蚀速率随流速呈指数变化;对比了不同流速、不同颗粒直径的最大冲蚀位置,其中最大冲蚀位置随流速的增加而增大,而颗粒直径对最大冲蚀位置的影响不大;分析了4种不同重力场条件下的冲蚀情况,当入口或出口方向与重力方向起正向叠加作用时,冲蚀较严重。

