哈夫曼编码方法的选择及其Python的实现
西北民族大学电气工程学院 冯兴民
随着人们对图像和视频的压缩存储和传输的要求越来越高,如何提高传输速率和如何节省存储空间显得更加重要,解决这两个问题的最根本途径就是采用图像压缩技术。本科课程《信息论与编码》中指出图像压缩的具体实现技术就是压缩编码,通过编码可以减少信息的冗余度从而提高传输速率和节省存储空间。在音视频编解码技术快速发展的今天,其实已经有很多的编码方法。通过实际应用发现,哈夫曼编码在编码效率与平均码长方面都是较好的。本文主要研究哈夫曼编码及其Python的实现。
1 哈夫曼编码
哈夫曼编码是一种典型的无失真编码,哈夫曼编码所采用的编码原理是最佳编码定理。最佳编码定理指出,在信息编码的过程中对于信源符号,如果分配短字长的码字给出现概率小的信源符号,分配长字长的码字给出现概率大的信源符号,那么编码结束之后所得到的平均码长一定是小于其他任何一种编码方法所得到的平均码长的,也就是每个信源符号所得到的码字长度是严格按照符号概率大小的相反顺序所排列。
哈夫曼编码具体步骤如下:
(1)将n个信源符号按其概率大小进行降序排序,即:

(2)取两个概率最小的信源符号分别配以1和0两个码元,然后将这两个信源符号概率相加作为一个新符号的概率,与未分配的二进符号重新进行降序排序。
(3)对重排后的序列重复(2)过程,直到只有两个信源符号为止,再把这两个信源符号分别配以1和0即可。
(4)最后得出各个符号的码字。
2 哈夫曼编码方法的选择及Python的实现
哈夫曼编码方法的选择和Python的实现看似是两个分离的部分,但其实两者是有机结合的,因为要对哈夫曼编码方法做出选择就要通过Python的实现来分析各种方法的平均码长和编码效率。由哈夫曼编码的具体步骤可以看出来:哈夫曼的编码结果其实是不唯一的。这是因为:其一,对两个概率最小的信源符号0和1的分配是任意的;其二,当两个概率最小的信源符号的概率相加时,所得的概率值有可能与原序列中的其他概率值相等。而这个相加的概率值可以在任意位置放置:放置在概率相同序列的最前端、最末端或者中间都是可以的,那么哪一种方法最好呢?这里主要分析在最前端和末端的情况。
首先进行哈夫曼编码的Python实现,因为只有用Python实现了哈夫曼编码才可以通过运行代码比较上面提到的两种哈夫曼编码方法的效率。由于哈夫曼编码的Python实现较于繁琐,因此在这里只给出部分核心代码。采用递归思想通过哈夫曼树来生成哈夫曼编码的核心代码如下:
def iscoding(self,tree,length):
node=tree
if (not node):
return
elif node._name:
print (node._name + ‘ encoding:’,end=’’),
for i in range(length):
print (self.Buffer[i],end=’’)
print (‘ ’)
return
self.Buffer[length]=0
self.iscoding(node._left,length+1)
self.Buffer[length]=1
self.iscoding(node._right,length+1)
def get_code(self):
self.iscoding(self.root,0) #采用递归方法来生成哈夫曼编码
哈夫曼编码用Python实现之后,用下面这个概率空间为例来进行分析和解释。已知概率空间,如表1所示。

表1 概率空间
表1所示的概率空间已经按照信源符号概率大小的降序进行排序,因此直接进行上面所提到的两种哈夫曼编码。
第一种:将概率最小的两个信源符号概率相加后排在其
如表3所示的这一种编码方法,是将概率最小的两个信源符号的概率相加所得的概率排在最末端的情况。
那么这一种方法的编码效率如何呢?还是和第一种方法一样通过运行Python代码,这儿的代码要进行一下修改以达到让两个信源符号概率和排到末端的目的。运行之后可以得到:其平均码长为2.2码元/符号,编码效率为96.5%,并且由Python代码运行出来的码字和表3的码字严格吻合。他相同概率序列的前面,其编码过程如表2所示。

表2 编码方法一

表3 编码方法二
如表2所示的这一种编码方法,是概率最小的两个信源符号概率相加之后排在最前端的情况;并且,从图中也可以看出信源符号出现的概率和码长是严格对应的,即概率大的符号配以短码长、概率小的符号配以长码长。这样做的原因是既然一个信源符号出现的概率大,也就是说在统计意义上这个信源符号在信息中出现的次数多,那我们就给他短的码长,这样既可以节省空间还可以提升传输速率。
那么这个方法的编码效率如何呢?通过运行上面的Python代码可以得到:其平均码长为2.2码元/符号,编码效率为96.5%,并且由Python代码运行出来的码字和表2的码字严格吻合。平均码长和编码效率的理论计算如下:
平均码长:
编码效率:
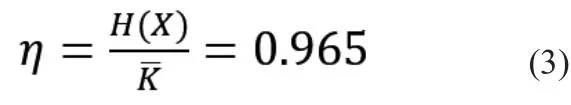
第二种:将概率最小的两个信源符号概率相加后排在其他相同概率序列的后面,其编码过程如表3所示。
由上面的分析可以得出:这两种方法的平均码长和编码效率是完全一样的,因此不能由平均码长和编码效率来区分出这两种编码的优劣。因此,通过码方差来判断这两种编码方法的优劣,码方差的理论计算公式为:
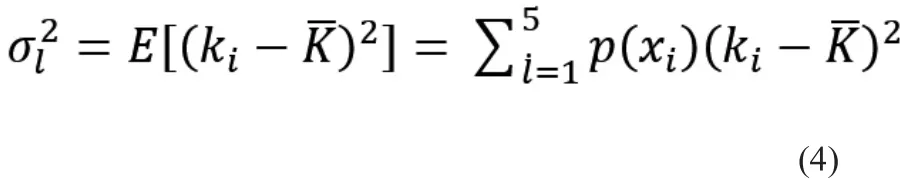
计算得到:第一种方法的码方差为0.16,第二种方法的码方差为1.36。由此可见,第一种编码方法的码方差较小,因此第一种编码方法更好。
总结:通过对上面这个概率空间的分析可以发现:在编码的过程中,在两个最小的概率符号相加之后,得到一个新的概率。而在实际应用和理论计算之后发现,这一个新的概率应该尽量放在相同概率的前面,这样才能保证这次编码有较好的平均码长、编码效率以及码方差。

