基于马尔科夫链模型的小金川河流域径流形势预估分析
陈仕军,王 亮,陈 刚,韩晓言
(1.四川大学水利水电学院,四川 成都 610065;2.国网四川省电力公司电力科学研究院,四川 成都 610041;3.国网四川省电力公司,四川 成都 610041)
0 引 言
径流预估一直是水文水资源利用研究领域的难点,准确可靠的径流预测是水资源规划调配、防洪减灾、防涝抗旱等重大决策的数据基础[1]。因此,研究一种精度较高且适用性强的径流形势预估方法具有重要的理论意义和实际意义。目前中长期径流预测的方法较多,传统的统计模型包括时间序列分析模型[2]、小波分析模型[3]、多元线性回归模型[4]等。由于大数据挖掘、人工智能的兴起,一些新的机器学习方法在径流预测中得到广泛的应用,主要包括人工神经网络模型[5-7]、支持向量机模型[8-10]、最近邻抽样回归模型[11-12]等。然而,这些方法对于研究区域的历史资料系列长度要求较高,在实际应用中往往受制于资料系列问题难以推广应用,因此希望通过运用水文领域经典的马尔科夫链模型对小金川河径流形势预估分析提供一种切实可行的思路和方法。
1 马尔科夫链模型基本原理
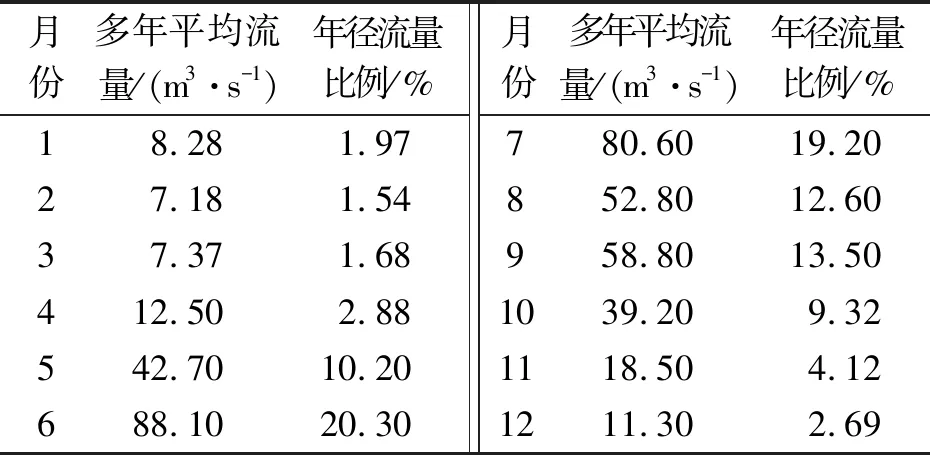
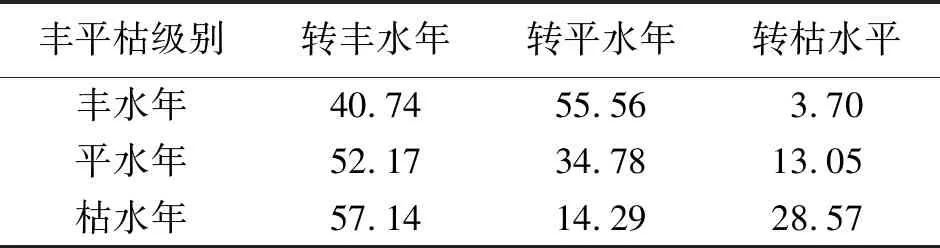
马尔科夫过程[13]的主要思路:当过程在时刻t0所处的状态为已知时,过程在t(>t0)所处的状态与过程t0时刻之前的状态无关,这种特性称为无后效性。用分布函数描述就是:如果对时间t的任意n个数值t1 F(xn;tn|xn-1,xn-2,…,x1;tn-1,tn-2,…,t1) =F(xn;tn|xn-1;tn-1 (1) 式中,n=3,4,…,则称X(t)为马尔科夫过程或简称马氏过程。式(1)右端的条件分布函数为F(x;tn|x′;t′)=P(X(t)≤x|X(t′)=x′),t>t′,称为马氏过程的转移概率。 式(1)等价于 f(xn;tn|xn-1,xn-2,…,t1) =f(xn;tn|xn-1;tn-1) (2) 式中,n=3,4,…。并由此证明X(t)的n维概率密度为 fn(x1,x2,…xn;t1,t2,…tn) (3) 式中,n=1,2,…。当取t1为初始时刻,f(x1;t1)为初始分布(密度)。式(3)表明马氏过程的统计特性由它的初始分布和转移概率所确定。 最简单的马氏过程是马氏链,即状态和时间参数都是离散的马氏过程。把状态转移时刻记为t1,t2,…,tn,在tn时刻发生的转移称为第n次转移;并假设在每一个时刻tn(n=1,2,…),Xn=X(tn)所可能取的状态(即可能值)为a1,a2,…,aN。这时,相应于式(1)有 (4) 如果进一步假设“在Xn-1=ai的条件下,第n次转移出现aj,即Xn=aj成立”的概率与n无关,那么可以把这个概率记为pij,即 (5) 由转移概率pij构成的矩阵,即 (6) 称其为马氏链的转移概率矩阵。该矩阵决定了X1,X2,…状态转移过程的概率法则。 小金川河是大渡河的一级支流,流域面积5275 km2,北源为抚边河,在猛固桥处与东源沃日河汇合后,始称小金川河。猛固桥往下,河谷逐渐拓宽,水流趋缓,水量增大。两岸集镇、耕地、人口增多。小金川河总长60.8 km,落差472.6 m,平均比降7.8‰,流经小金县、丹巴县。 小金川流域共规划了13级电站。支流抚边河上有5级,分别为焦家、美卧、木坡、杨家湾、猛固桥水电站,其中美卧为龙头水库;支流沃日河上有4级,分别为日尔、中马厂、官寨、春厂坝水电站;小金川干流上有4级,分别为马桑寨、小金、三叉、太平水电站。结合小金川河流域水电站建设和地理位置情况,选取木坡水电站进行径流形势预估分析的实例研究。 小金川流域径流在年内的变化与降雨基本相应。每年4月起径流随降水的增加而逐渐增加,6、7两月水量最充沛,9月次之,11月以后由于降水量的降低,径流开始以地下水补充为主,稳定退水至次年3月。径流年内分配极不均匀,主要集中于汛期。 木坡水电站丰水期(5月至10月)流量约占年径流量的85.0%,多年平均流量为60.2 m3/s,其中最丰的6、7两个月多年平均流量为84.3 m3/s,约占年径流量的39.4%。枯水期(11月至第2年4月)流量约占年径流量的15.0%,多年平均流量为10.9 m3/s,最枯段(1月至3月)多年平均流量为7.62 m3/s,约占年径流量的5.3%,最枯的2月份,多年平均流量为7.18 m3/s。年最大流量出现在5月下旬至7月,实测最大流量261 m3/s(1964年6月30日)。年最小流量一般出现在2、3月,最小月平均流量5.82 m3/s(1968年2月)。 木坡水电站多年平均流量及其年内分配如表1所示。径流年际间变化不大。木坡水电站最大年平均流量为48.2 m3/s(1965年),最小年平均流量为29.8 m3/s(1967年),分别为多年平均流量的1.35倍和0.83倍,最大与最小之比是1.62。 表1 木坡水电站月平均流量统计 根据马尔科夫链原理,对小金川流域径流形势进行预估的具体步骤如下: 1)排频分析:对历史资料中木坡水电站1959—2016年的年平均流量按照从大到小的顺序进行排列,并计算对应的频率,确定木坡水电站年平均流量的频率曲线。 2)丰平枯水电划分:在木坡水电站年平均流量的频率曲线,以频率30%及70%为界(木坡水电站Q70%=30.5 m3/s,Q30%=36.8 m3/s),将长系列径流过程划分成3种情况,确定每年的径流丰枯情况。其中,Q>Q30%为丰水年,Q 3)流量丰枯变化统计:按照年份从小到大的顺序,分别统计上一年为丰水年且下一年为丰水年、平水年、枯水年的年数,上一年为平水年且下一年为丰水年、平水年、枯水年的年数,上一年为枯水年且下一年为丰水年、平水年、枯水年的年数。 4)丰枯转换概率计算:计算出木坡水电站历史径流系列中丰水年、平水年、枯水年相互转变的马尔科夫一步转移概率,如表2所示。 5)根据表2中的木坡水电站年平均流量转移概率表,可以结合当年来水丰枯情况,对木坡水电站下一年来水丰枯形势进行预估。 以2018年木坡水电站的丰枯形势预估为例,2017年木坡水电站的平均流量为37.91 m3/s,属丰水年,根据木坡站年平均流量转移概率表,2018年为平水年的概率最大,为0.555 6;2018年实测年平均流量为36.01 m3/s,为平水年,与预测结果一致。由此可见,所建立的木坡水电站年平均流量转移概率表可用于指导小金川河流域的径流形势预估。 表2 木坡水电站年平均流量转移概率单位:% 基于马尔科夫链模型进行年径流形势预估,建立了小金川河流域木坡水电站年平均径流丰枯转换的马尔科夫一步转移概率表,并以2018年木坡水电站的丰枯形势预估为例进行实例分析,验证了运用马尔科夫链模型预测小金川河流域径流形势的可行性,该方法可为径流形势预估分析提供一种切实可行的思路和方法。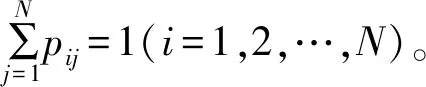
2 径流形势预估实例研究
2.1 研究区域概况
2.2 流域径流特性分析
2.3 径流形势预估及结果分析
3 结 语

