复杂电网级联事故下的重要线路辨识

曾阳阳，关翔友，徐 昆，刘闻博，姜婷菡，范珺阳

(1.四川大学电气工程学院，四川 成都 610065；2.国网哈尔滨供电公司，黑龙江 哈尔滨 150036)

0 引 言

近年来，世界范围内频繁发生的由级联事故造成的大范围电力供应中断事件，给全社会造成了巨大的经济损失甚至人员伤亡，也给网络安全研究人员敲响了警钟[1-2]。研究表明，级联事故往往是由电网中某一元件故障引起系统中其他元件连锁失效造成的。例如在2003年发生的美国和加拿大地区的大停电事故，其触发因素是树枝意外与一回高压线路接触后造成线路接地短路后断开，潮流转移引起的诸多突发事故造成连锁效应累积后的大范围停电。文献[3-5]中均指出，电网中存在重要元件(节点或线路)，其故障后引起电网潮流大范围的重新分配和诸多电气量的振荡变化，在级联事故的发生和扩散过程中起到关键作用。因此，准确识别电力网络中退出运行后能造成大范围级联事故的线路，并按照其造成事故危害程度对线路重要度进行排序，对电力系统级联事故控制有着重要意义。

基于此，全世界研究学者围绕电力系统关键线路识别展开了相关研究，当前主要研究方法可分为两大类[6]。第一类研究是基于还原论和电网动态特性等传统方法，以潮流计算和系统暂态稳定分析等为主要手段，通过级联事故仿真推演出系统状态的发展趋势，有针对性地进行电力系统状态评估和脆弱性辨识；第二类研究应用复杂网络理论，以电网拓扑结构为研究对象，借助节点(或线路)的度和介数等指标，对电网元件的重要程度进行评估。

电网是内部包含大量动态原件构成的复杂非线性动力学系统，电网级联事故扩散过程中往往伴随着功率振荡、潮流转移和电压波动等诸多复杂现象。但是在第一类研究方法中大多选取上述电气量中单方面因素作为扩散依据，例如经典OPA模型[7-8]仅以线路有功潮流转移越限为级联事故扩散依据，忽略了电压和功角等诸多关键电气量的振荡波动，过于片面，其仿真结果与电网事故扩散特征有较大差别。基于此，文献[9]在分析电网级联事故脆弱性时，将潮流转移、电压波动和电压相角等诸多电气量变化在能量函数计算表达式中统一表达，即实现了电网级联扩散关键驱动力的同一性建模。由于其全面性和有效性，能量函数在电网级联事故的分析当中得到广泛应用[10-12]。第二类研究方法中，若仅从电网拓扑结构角度对网络元件的重要度进行评估，即其结果在网络任何运行方式下重要线路辨识结果一致。这类方法只在意系统中的内在结构短板，却忽略了外在运行风险。而在运用能量函数构造出的复杂网络模型中，除运行状态外，网络拓扑结构也对网络元件间能量关系起到关键作用。即该模型综合考虑了电力系统级联事故扩散过程中各类电气量之间的关联方式和电网本身的拓扑结构特性。

综上，运用能量函数和直接法的建模思想，全面量化网络线路之间的关联关系，构造出以线路为基本结构单元、以线路间能量关联关系为权重的适用于电网级联事故分析的复杂网络模型；然后，对复杂网络理论中的网络能力(net-ability，NT)指标进行适应性改良，在所提的复杂网络模型环境内，提出线路重要度评估指标；最后，通过基于OPA模型的电网级联事故仿真对所提出的指标有效性进行了验证，并结合试验结果为电网级联事故预防及控制提出新的研究思路和意见。

1 基于能量函数的复杂网络模型

1.1 能量转移冲击

对于稳定运行中的电网，短路、断线等大扰动除了会严重威胁其暂态稳定性以外，还会进一步触发连锁效应造成大范围停电事故。潮流重新分配可能会出现有功功率越限且伴随诸多电气量的波动振荡现象。电网调度人员会通过多类技术手段保证电网各项电气指标不越限，维持电力系统可靠运行。一般情况下，通过直流优化计算来表述上述调整过程，如式(1)所示。

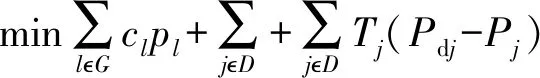
(1)

式中：目标函数为当系统受到大扰动后调度部门改变发电机出力并且切负荷措施造成的经济损失之和最小；pi为电网中所有节点的注入有功功率；D和G分别为电网中负荷节点和发电机节点的集合；cl和pl分别为调整后发电机产生单位出力的所需费用和调整后发电机的有功出力；Pdj为节点j的负荷需求；Pj为调整后节点j的实际负荷；Tj为切除单位负荷对系统造成的经济损失，一般情况下要求Tj≫cl；最后3个约束是为保证调整措施执行后节点负荷不超过实际负荷需求的上限，各发电机出力和各线路潮流不超越其上下限。该模型求解为混合整数规划问题(mixed integer linear programming)，需利用Cplex求解。

在稳定运行状态下，电网支路k(其首末端节点为i和j)的初始有功潮流和无功潮流分别为Pij，s、Qij，s。电力网络拓扑结构改变引起支路上的电气量发生变化，系统中可能某些线路受能量冲击过大，系统安全受到威胁。采用直接法的建模方式[13-14]，若线路l断开，经直流潮流优化过程处理后，导致线路k所受能量冲击为

(2)

式中：fpij和fqij为线路l断开后，经过直流优化过程后的线路k上的有功潮流和无功潮流的变化量。根据线路之间的有功和无功功率传输关系可知：

fpij=Pij-Pij，s

(3)

(4)

将式(3)、式(4)带入式(2)中，得出线路l断开后，线路k所受能量转移冲击为

(5)

式(3)至式(5)中：δi和δj是对应端点电压的相角，δij=δi-δj；Uij为节点i和j之间电压幅值差，Uij=Ui-Uj；下标s代表初始值。

El→k的物理意义为线路l断开后线路k上各类电气量变化，电气量偏离初始值越大，支路k所受到的能量冲击越大。

1.2 线路间能量关联关系

线路意外断开导致其他线路电气量改变，形成能量冲击；但另一方面，若受冲击线路承载能量冲击极限足够大，该线路也不会因为过载而级联断开。综合上述两个因素，线路l(k)断开对线路k(l)运行稳定性的影响可定量描述为Rl→k(Rk→l)。由此，定义线路间能量关联关系为：

(6)

(7)

(8)

其中：

(9)

(10)

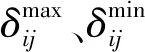
如式(6)所示，当线路l意外断开对线路k的能量作用越接近线路k的承载极限，则线路l所发生事故对线路k造成的影响越大，该式函数值越小，从级联效应来说，两者关联作用影响越大。以线路之间的相对能量传递作用关系Rlk为关联关系权重，可构造出以线路为基本结构单元的加权无向的复杂网络模型。该模型的状态关联矩阵是由Rlk为元素组成的“复杂网络系统作用关系相对矩阵”R为

(11)

式中，矩阵为对称矩阵，Rlk=Rkl，对角线元素为0。在该矩阵的基础上，可构建出线路为基本结构单元、线路之间能量关联关系为权重的加权无向网络模型，为线路重要度指标提取提供执行环境。

2 线路重要度指标

2.1 网络能力

为量化描述电力网络中每条线路在潮流输送中的贡献，文献[15-16]定义了功率传输分布因子(power transmission distribution factors，PTDF)矩阵F，反映了网络潮流对一对发电机节点和负载节点之间传输功率变化的灵敏度。对于确定的网络结构，可由矩阵F推导出的网络能力(net-ability，NT)指标从网架拓扑结构的角度量化网络整体性能。若一条线路断开后网络NT值下降的幅值越大，从结构上讲，这条线路对电网运行越重要。为实现网络能力对电网运行影响的评估，在综合考虑电网内在结构短板和外部运行风险后，文献[17-18]结合了通信网络中流量和有效性能的概念，定义了适用于电网状态分析的网络能力。

(12)

式中：Ng和Nl分别为电力系统中发电和负荷节点的数目；Sg和Sl分别为发电机和负荷节点的集合；Tgl为节点g和l之间的有功传输极限；Zgl，equ为节点g和l之间的电气距离。数值上：

Zgl，equ=(Zgg-Zgl)-(Zgl-Zll)

(13)

式中，Zgg、Zgl、Zll为网络节点阻抗矩阵中对应位置元素。

由此，给出电网中节点流量概念，用以评估网络中节点重要程度，其物理意义为节点i故障移除后，网络能力下降越多，节点在电网稳定运行中越关键。

(14)

式中，PY和PY-i分别为电网正常运行和节点i故障移除后的网络能力大小。

2.2 线路重要度指标

如前所述，在以线路为基本结构单元、线路之间能量传输关系为权重的复杂网络的执行环境内，对网络能力进行适应性改良，提出网络能量传输能力CY概念，用以评估网络整体性能。

(15)

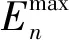
关于权重，根据网络结构单元之间关联关系赋予方式和物理意义的不同可分为两大类：1)相似权，其特征为权重越大则结构单元之间的关联越紧密；2)相异权，其特征为权重值越大则结构单元之间关联越弱，例如线路阻抗、节点之间距离等。根据网络能量关联关系定义可知，Rmn值越小，表征线路m、n之间关联关系越强，属相异权。由文献[19]可知，式(12)中电气距离同属相异权。因此，从关联关系角度，线路间能量关联R矩阵中元素与线路阻抗有相同物理意义。因此，在所定义的复杂网络模型下，线路m、n之间的电气距离定义为

Zmn=Rmn

(16)

基于此，将线路移除后，将电网能量传输能力变化量定义为输电线路的重要度指标判据，网络线路能量流量Li计算公式为

(17)

式中：CY为电网Y正常运行时的网络能量传输能力；CY-i是电网Y移除线路i后网络能量传输能力。Li值越大，表示线路i在电网运行中的地位越关键。

3 算 例

3.1 构造复杂网络模型

以matpower数据包中的IEEE-39系统作为算例执行环境，系统中共有39个节点，共有线路46条，将储存线路数据的mpc.branch矩阵中线路所在行数作为网络中线路序号，如图1所示。

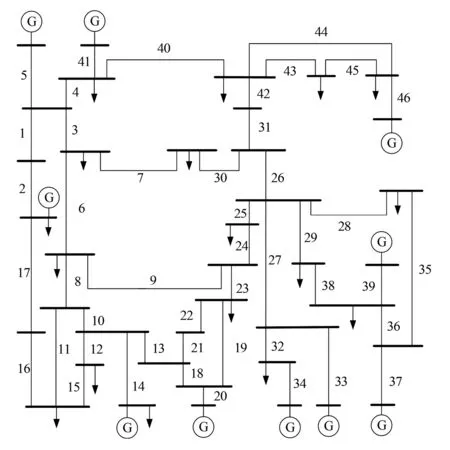
图1 IEEE-39节点电力系统拓扑分布

依次断开网络中所有线路，并求取该线路断开后受冲击线路的冲击能量大小，并按照式(6)至式(10)计算两线路之间的能量关联关系。由此求取线路之间作用关系相对矩阵，矩阵元素分布如图2所示。

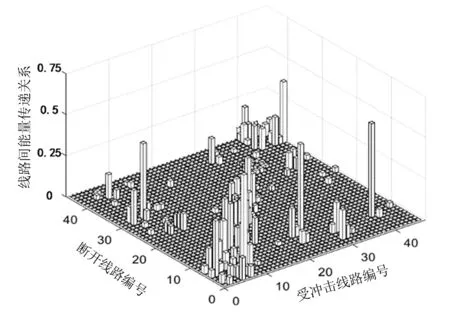
图2 线路间能量传输分布

可见，矩阵中元素主要集中在对角线，表示线路断开对临近线路的能量冲击最大，并以断开线路为中心向外逐渐减弱。说明能量函数能够很好表示实际线路之间的能量关联关系，且能定量描述拓扑关系上距离较远的线路间能量关系。由此，可构建出以线路为基本结构单元、线路之间能量关联关系为权重的加权无向网络模型。

3.2 线路能量流量指标提取

首先，计算出电网初始运行状态下网络能量传输能力CY。依次断开网络中线路，计算线路i断开后网络的能量传输能力CY-1。由式(17)计算每条线路的能量流量Li结果，如表1所示，所有数据保留3位小数。

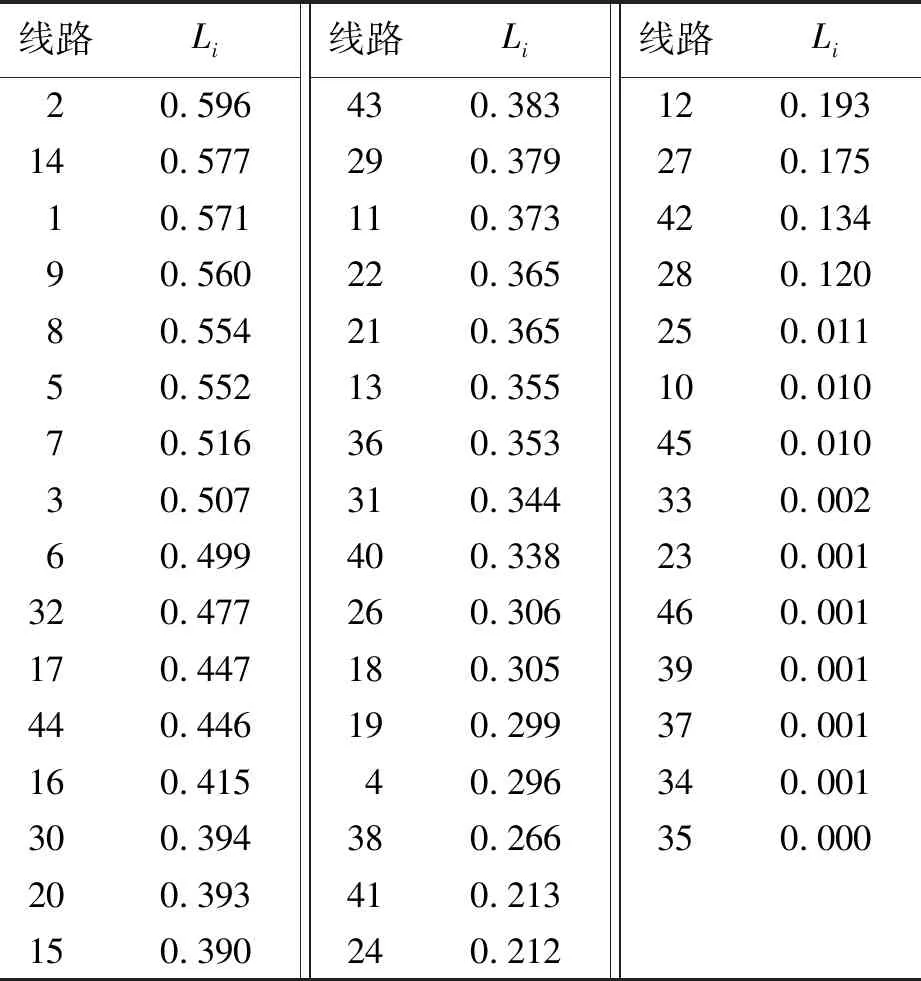
表1 各线路的能量流量

按上述线路重要度指标物理意义可知，该指标数值越大，其故障后引起的级联事故范围越大。以级联事故结束后网络中的负荷损失百分比作为级联事故规模的评估指标，遍历各线路断线后的电网级联事故规模，并通过求取与各线路重要度指标的相关系数，验证重要度指标的有效性。

3.3 重要度指标有效性验证

2002年，D. E. Newman 和Dobson I等人[7]建立了OPA 模型，用于仿真电网级联事故，推演事故扩散规律，并已得到广泛应用。该模型包含两个时间维度：外层是慢动态过程，用于仿真电网中负荷需求不断增加和电网的升级改造；内层为快动态过程，用于模拟电网级联事故的扩散过程。然而，如前文所述，OPA原模型存在不足，以基于能量函数的能量转移冲击作用为判据，结合直流优化模型，通过更改级联事故驱动因素对OPA模型进行适应性改进，具体操作流程如图3所示。

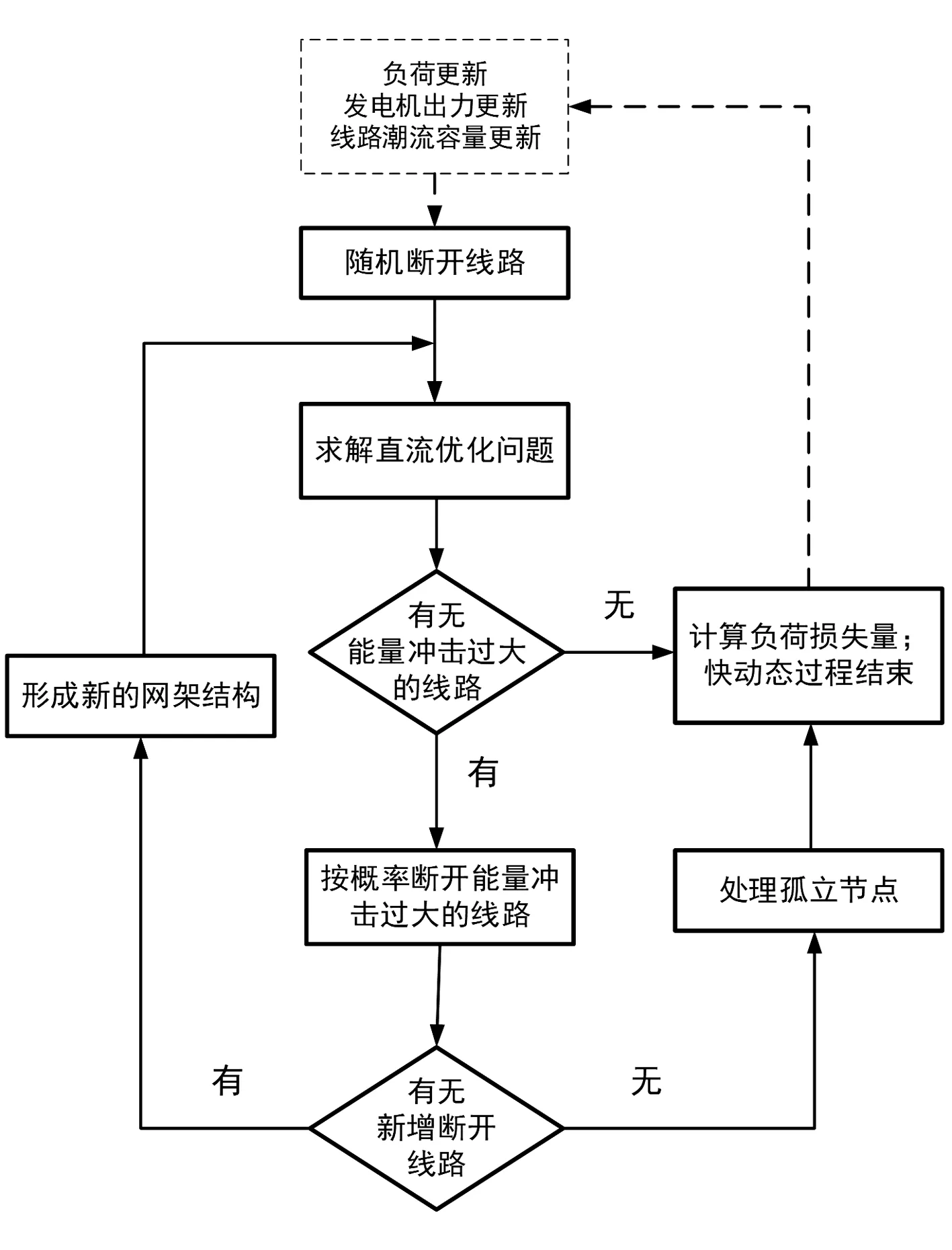
图3 改进OPA模型流程

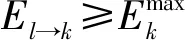
图4 线路重要度指标与平均事故规模的拟合直线

图中虚框内的点为重要度指标很小的线路在其断线后所造成的级联事故规模，可见这些线路造成的负荷损失很小。对能造成一定规模级联事故的线路，求取其平均事故规模与其能量流量的相关系数为0.872 7，属强正相关。因此，线路能量流量可有效量化线路在级联事故发生过程中的关键程度。

4 结 语

以能量函数为基本数学工具，结合直接法建模方式，准确量化网络线路之间的能量传输关系后，建立了以线路为基本结构单元的复杂网络模型；在PTDF网络能力的启发下，在上述复杂网络模型的执行环境内，提出线路能量流量的概念，用于评估网络线路在级联事故发生过程中的关键程度；最后，在IEEE-39节点系统内进行的级联事故仿真证明了所提的线路关键指标的有效性，对电网级联事故的预防分析与控制有积极意义。