移动型数据与静态型数据的混合聚类算法

何云斌, 董 恒, 万 静

(哈尔滨理工大学 计算机科学与技术学院, 哈尔滨 150080)

0 引 言

聚类分析是数据挖掘与机器学习中十分重要的一个研究领域，是在没有先验知识的情况下对数据进行分类，并以此分析数据的特点。经典聚类算法K-means算法[1]，简单高效、适用范围广，但是对聚类中心较为敏感，只能识别出球形簇。后来，科研工作者提出基于密度的聚类算法，克服了K-means的缺点，比如Huang等[2]提出了一种基于网格和基于密度的混合聚类算法GRPDBSCAN，该算法可以有效处理噪声点，且运算速率较高，自动生成邻域参数(ε,MinPts)。文[3]针对DPC算法在寻找聚类中心的过程时，计算复杂度高，无法在大规模数据集中应用的问题，提出基于网格筛选的SDPC算法。文[4]提出两步操作的改进K-means算法，将算法在MapReduce模型上进行实现。

这些聚类算法是针对静态型数据的聚类分析，在对静态型数据进行处理时，可以产生比较良好的聚类效果，但是对于移动型数据却难以奏效。这主要因为移动型数据具有移动特性，因此对于移动型数据的聚类处理，传统聚类算法处理效果较差，研究人员转向对移动型数据的聚类研究。

Kalnis[5]基于连续快照模型，提出了Moving Cluster模式，通过使用空间聚类算法对每张时间快照上的移动数据进行聚类处理，然后通过对比连续时间快照上簇之间Jaccard系数是否超过给定阈值，以判断移动数据是否组成Moving Cluster模式。在Moving Cluster基础上，科研工作者进行了改进，提出了Convoy[6]模式，并进一步提出了Swarm[7]模式。文[8]提出在开始先对快照上的移动对象进行聚类，然后在已有的聚类簇上使用KDS[9](动态数据结构)进行维护和修改。文[10]也是以连续快照模型，将DBSCAN算法改进并应用到移动对象上面，并提出基于时空图的移动对象聚集检索算法。文[11]提出一种并行算法RDD-Gathering来发现大规模轨迹数据中的聚集模式。文[12]提出了一种新型的群体模式，称为进化群体，它模拟在不断变化的流动轨迹中密度连通群集内一起行进的移动物体的异常群体事件。

在经过大量的文献查询和分析，发现目前已有针对混合数据类型的聚类算法中，经典的k-prototypes聚类算法,虽然针对同时具有数值属性和分类属性的混合数据简单高效,但是算法易受初始聚类中心影响[13]。文[14]针对兼具数值属性与分类属性的不完备混合数据，提出三种完备化处理方法，并采用k-prototypes算法进行聚类处理。文[15]也是针对同时具有数值属性和分类属性的混合数据聚类，提出了基于信息熵的混合数据属性加权聚类算法。文[16]针对k-prototypes算法无法自动识别簇数以及无法发现任意形状的簇的问题,提出一种针对混合型数据的新方法。虽然这些研究是针对混合数据属性，但是并非从数据的状态混合出发，因此针对包含静态型数据与移动型数据的混合聚类问题也无法有效处理。本文针对包含静态型数据与移动型数据的混合数据的聚类问题，进行讨论和分析并给出相应的聚类算法。

本文的主要贡献：针对目前没有包含移动型数据与静态型数据的混合数据聚类问题的算法，本文根据已有的处理静态型数据的聚类算法和移动型数据的聚类算法的优缺点，基于“分而治之”的思想，提出针对混合数据的聚类算法。在具体方法上则提出将处理移动型数据的连续快照模型结合处理静态型数据的密度化处理方法，以时间为主线，对混合数据进行聚类分析。

1 相关概念与定义

给定欧式空间中，移动数据集M={m1,m2,…,mp}，静态数据集S={s1,s2,…,sq}，基于以上概念，进一步给出如下定义。

定义1(时间快照) 设混合对象数据库是ODB={M,S}，与它相对应的时间数据库TDB，时间快照Pi={(ai,ti)|ai∈ODB,ti∈TDB}，其中Pi是对应时间ti的时间快照，是时间快照集合P的子集。

定义2(移动对象聚类[10]) 令集合ci={m1,m2,…,mp}是对应于每一个时间i(1≤i≤k)的移动对象集合，对于两个给定的阈值nc和kc，当满足以下条件时，ci是一个移动对象聚类：

1)ci中的成员数量size(ci)≥nc;

2)ci存在一段时间，即生存时间time(ci)≥kc;

3)ci包含的任意两个移动对象mk和mr的距离不大于δ，可以表示为dist(mk,mr)≤δ，其中，∀mk,mr∈M。

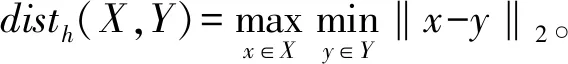
2 算法描述

目前已有的聚类算法研究都是围绕单一数据类型的聚类问题展开，对于包含移动型数据与静态型数据的混合数据聚类问题，则没有相应的讨论和研究，下面首先从单个的移动型数据与静态型数据集的聚类问题开始分析。

2.1 一个移动型数据与静态型数据集的聚类算法

问题描述：若在给定欧式空间中，有一个随机移动的移动型数据m和位置随机分布的静态型数据集S构成的混合数据H，如何对混合数据H进行聚类处理，本节进行讨论和分析，并给出相应的聚类算法。

混合数据最大的特点就是不同的数据类型交织在一起，如果直接对其进行聚类处理，则会比较困难。因此提出应用“分而治之”的思想，将不同的数据分开处理，然后再合并处理。在本文中就是先将静态型数据与移动型数据分开进行聚类处理，然后再进行合并聚类处理。

为了便于对混合数据进行聚类分析，采用时间快照的方法，因为时间快照可以完整将数据间的相对位置和移动物体的历史移动轨迹记录下来。为了能对记录下来的数据类型进行区分，以便于后续分析，在采集时间快照时，对不同的数据类型进行标记，以作区分。聚类的准确性和精确度可以通过缩短时间快照的间隔时间进行提高。

对于静态型数据集内随机分布的静态型数据，为了能够发现任意形状的静态簇，提高聚类效果，本文选择基于密度的DBSCAN[2]算法。由于静态型数据的位置不再发生变化，因此只需进行一次聚类处理即可，对静态型数据处理完毕之后，可以得到一组静态簇SC。然后对移动数据进行处理分析，由于本节研究的问题只涉及一个移动型数据，因此从单个移动型数据与静态型数据集的聚类问题就转变成一个移动型数据归属哪个静态簇的问题。

在每张时间快照下移动数据的位置都是不一样的，因而对移动数据与静态数据之间的相似度判断不能简单应用处理静态数据之间相似度关系的方法进行处理。而是基于“共现”思想，采用定义3的Housdorff距离作为移动型数据与静态簇之间的相似性度量标准并且结合时间属性，根据判断规则1综合判断移动型数据归属于哪个静态簇。

判断规则1给定一个移动数据m，对静态数据集聚类处理过后的静态簇集合SC={sc1,sc2,…,sck}，距离阈值δ，时间阈值kt，当移动数据m与∃sc∈SC满足以下条件时，则移动数据m∈sc，否则移动数据m为离群点。

1)在静态簇集合SC中有一个静态簇sc与移动数据m的距离不大于δ，表示为distH(sc,m)≤δ，其中∃sc∈SC；

2)若满足条件1)中移动数据m和静态簇sc的持续时间不小于时间阈值kt，则将移动数据m归属于静态簇sc。

判断规则1中的时间阈值由人工设置，阈值设置的过长或过短都会导致错误的判断，比如阈值取整个时间范围的值，那么只有从开始到结束，在距离上一直相近的数据才能划分为一类，那就失去了聚类分析的意义。假如阈值取为单位时间，每个单位时间内，距离相近都被划分一类，不符合对混合数据聚类的划分规则。

图1 单移动数据与静态数据集聚类示意图Fig.1 Schematic diagram of single mobile data and static data set clustering

下面给出包含一个移动型数据与静态型数据集的混合数据聚类的示例。如图1所示，给定混合数据H，H包含有静态型数据集S和一个移动型数据m，时间阈值设置为3，此处时间阈值为人工设定。首先对静态型数据集S进行聚类处理后得到静态簇集合SC={sc1,sc2}，然后对每张时间快照进行扫描，移动型数据m与各个静态簇之间应用Housdorff距离进行相似性度量，图中虚线代表了移动数据与静态簇之间的距离小于距离阈值，并且持续时间不小于3个时间快照，因此在t3时刻，用实线将静态簇sc1与移动数据圈在了一起，移动数据被划分入了静态簇sc1。

基于以上讨论和分析以及判断规则1,现在给出SMPSP(一个移动型数据与静态型数据集)算法的主要思想：首先对静态型数据集应用DBSCAN算法，对应算法第3～4步，当得到静态簇SC={sc1,sc2,…,sck}之后，扫描每张时间快照，获得每张时间快照上所有数据的位置分布和数据的类型，使用Housdorff距离度量移动型数据m与每个静态簇sc之间的距离，若出现某个静态簇sc与移动型数据m之间的距离小于给定距离阈值δ时，将其记录下来，对应算法6～16步。然后重复上述步骤处理接下来的时间快照，并记录下移动型数据与已有静态簇之间的距离distH(sc,m)，并根据判断规则1，对应算法的第7～11步，进行判断移动型数据m与静态簇sc之间的关系。

算法1 SMPSP

输入：移动型数据m，静态型数据集S={s1,s2,…,sz}，距离阈值δ，时间阈值kt，邻域参数(ε,MinPts)，时间快照的张数p

输出：聚类结果hc

//tmp的结构为(簇；簇出现次数,初值为0)

1.tmp←∅

2.hc←∅ //最终结果簇集合

3.SC←∅ //静态簇集合

4.SC←DBSCAN(S,ε,MinPts)

5.fori:=1top//从头至尾遍历时间快照

6. forj:=1tok// 遍历每个静态簇

//判断静态簇与移动型数据m是否满足距离

//阈值的限制和与上一张时间快照内的静态

//簇是否相同

7. if(distH(scj,m)≤δand

previous(tmp·sc)==scj) then

8.tmp←(scj,times+1)

9. if(tmp·times≥kt) then

10.hc←hc(i,(scj,m))

11.hc←hc(i,(SCscj))

12. end if

13. end if

14. else

15.tmp←∅

16.hc←hc(i,SC)

17.end for

18.end for

19.returnhc

算法时间复杂度分析：根据文[18]得到步骤4调用DBSCAN算法的时间复杂度为O(z2)，z为静态点的个数，步骤5～16之间为判断移动型数据m的归属问题，只有一个for循环，因此步骤6～16的时间复杂度取决于静态簇的个数k(k≪z)，在整个算法中，还有步骤3的一个for循环遍历整个时间快照。综上所述，算法1的总时间复杂度为O(z2+pk))。

2.2 移动数据集与静态数据集的聚类算法

当移动型数据不再单一时，包含一个移动型数据与静态型数据集的混合数据聚类问题也就变成了包含移动型数据集与静态型数据集的混合数据聚类问题，具体可描述为：给定一组包含移动型数据集M={m1,m2,…,my}，静态数据集S={s1,s2,…,sz}的混合数据H，对混合数据H进行聚类分析。

由于移动型数据的增多，聚类问题复杂化，在整个聚类思想上依然与一个移动型数据与静态型数据集一样，采取“分而治之”的思想，但是在后续具体的聚类处理方法上有所不同。首先，针对移动型数据与静态型数据同时存在的问题，采取对不同类型的数据进行标记的方法，以便后续的聚类处理。对于混合数据中的静态数据集，采用基于密度的DBSCAN聚类算法，理由与2.1节中相同，在此不再赘述，通过对静态型数据集的聚类处理，可以获得一组静态簇SC。对于混合数据中的移动数据集，不再采取对一个一个移动型数据和所有的静态簇进行相似性度量，然后把一个一个移动型数据划分到不同簇中的模式，因为在大量的移动型数据下，这么做计算量实在过于庞大，而且各种情况比较复杂，不便处理。本文提出下述方法，首先采取定义2的移动聚类方法对移动型数据集进行处理，获得一组移动簇MC，然后通过对静态簇与移动簇进行相似性判断，进而获得聚类划分。

至此，在整个针对包含移动数据集与静态数据集的混合数据的聚类问题处理中，我们得到了一组静态簇和一组移动簇。因为移动簇由移动数据组成，因此移动簇必然也是随着时间而进行移动的。所以在簇的层面上，移动簇与移动簇，移动簇与静态簇之间发生聚集也是很有可能的。从移动数据集与静态数据集的聚类问题转变成了簇与簇的聚集问题，具体可描述为：给定欧式空间中，移动簇集合MC={mc1,mc2,…,mck}，静态簇集合SC={sc1,sc2,…,scl} ，距离阈值δ，时间阈值kt，若满足判断规则2，则称两个簇发生了聚集。

判断规则21)两个簇之间的距离不大于距离阈值δ，即distH(mca,scd)≤δordistH(mca,mcb)≤δ，其中∀mca,mcb∈MC，∀scd∈SC。

2)满足条件一的两个簇的存在时间不小于时间阈值kt，即time(mca,mcb)≥ktortime(mca,scd)≥kt，其中∀mca,mcb∈MC，∀scd∈SC。

如图2所示，设置时间阈值为3，在t1～t66张时间快照中，有3个移动型数据在t1～t3的3张时间快照中，距离相近，在t3时刻，这3个移动型数据组成了1个移动簇，虚线圈变成了实线圈，而在t4～t6时，移动簇与静态簇sc2距离相近，并且持续时间一直到t6，所以在t6时刻，移动簇与静态簇sc2，聚集成1个新簇。

基于以上讨论和分析，给出算法MMPSP的主要思想：首先对静态型数据集S应用DBSCAN算法，得到静态簇，然后对每张时间快照上的移动型数据集M应用定义2的移动聚类方法，得到移动簇，对应算法的第8步。使用存储结构HTMP用于存储移动簇与静态簇，存储结构MTMP存储移动簇与移动簇的出现聚集次数的情况，聚集次数的初始值为0。应用判断规则2对移动簇与静态簇之间的关系判断，并将结果存储到hc中，对应算法的第9～22步。再对移动簇与移动簇之间的关系做判断，并将结果存储到hc中，对应算法的第23～35步，最后返回聚类结果hc。

图2 移动数据集与静态数据集的聚类示意图Fig.2 Clustering diagram of mobile datasets and static datasets

算法2 MMPSP

输入：移动数据集M={m1,m2,…,my}，静态数据集S={s1,s2,…,sz}，距离阈值δ，时间阈值kt，邻域参数(ε,MinPts)，时间快照的张数p

输出：聚类结果hc

1.MC←∅ //移动簇集合

2.HTMP←∅

3.MTMP←∅

4.hc←∅ //最终结果簇集合

5.SC←∅ //静态簇集合

6.SC←DBSCAN(S,ε,MinPts)

7.fori:=1top//遍历每张时间快照

//定义2

8.MC←moveCluster(δ,kt,M)

9. fora:=1 toSC.length

10. forb:=1 toMC.length

//判断两个簇距离和前一张时间快照内是否

//为这两个簇

11. if(distH(sca,mcb)≤δand

previous(sc,mc)==(sca,mcb)) then

12.HTMP←

htmp((sca,mcb),times+1)

13. elseHTMP←

htmp((sca,mcb),0)

14. end for

15. end for

//筛选出HTMP中符合判断规则2的簇

16.forj:=1 toHTMP.length

17. if(htmpj.times≥kt) then

18.hc←hc(i,(htmpj.(mc,sc))

19.hc←hc(i,(MChtmpj.mc))

20.hc←hc(i,(SChtmpj.sc)

21. end if

22.end for

23.fora:=1 toMC.length

24. forb:=1 toMC.length

//pervious()表示与上一张时间快照的数据

25. if(distH(mca,mcb)≤δand

previous(sc,mc)==(sca,mcb)) then

26.MTMP←

mtmp((mca,mcb),times+1)

27. elseMTMP←

mtmp((mca,mcb),0)

28. end for

29. end for

//筛选MTMP中符合判断规则2的簇

30. forj:=1 toMTMP.length

31. if(mtmpj.times≥kt) then

32.hc←hc(i,mtmpj(mc1,mc2)

33.hc←hc(i,(MCmtmpj.(mc1,mc2))

34. end if

35.end for

36.end for

37.returnhc

算法时间复杂度分析：在第7步调用DBSCAN算法，根据文[18]可知，时间复杂度为O(z2)，z表示静态型数据的个数，在利用定义2对移动型数据集的聚类问题上，根据文[10]应用的针对移动型数据的改进DBSCAN算法，时间复杂度也为O(y2)，y表示移动点的个数，在后续应用判断规则2对簇之间的关系进行判断时，用到了双层for循环遍历，因此时间复杂度度也为O(kl+k2)，其中k表示的是形成移动簇的个数，l表示的是形成的静态簇的个数。最后加上遍历整个时间快照。因此，总时间复杂度为O(z2+p(y2+kl+k2))。

3 实验结果与分析

本文研究的是包含静态型数据与移动型数据的混合聚类问题，将这些数据抽象在二维空间下进行研究，使用Housdorff距离度量数据之间的相似度，并结合“共现”思想，判断是否相似而划分为一类。

本文的数据是指包含移动型数据与静态型数据的混合数据，目前已有的处理混合数据研究，是针对数值型数据和分类型数据的混合数据，而没有针对数据状态的混合，即对静态型和移动型数据的混合。因此本文的对比实验算法选择了处理静态型数据的SDPC[3]聚类算法和处理移动数据的TAD[19]聚类算法，作为对比算法进行对比实验。

在对一个聚类算法进行评价时，通常会从F-meature指标和Silhouette指标进行评价，它们的取值范围均为[0,1]，并且越接近1，说明效果越好。本文从F值指标与S值指标以及运行效率等方面评价算法聚类效果。

实验的数据集采用真实的GPS轨迹数据(http://www.ccf.org.cn/sites/ccf/dashuju.jsp?contentId=2756825351305#大赛赛题)，选择的是2012年11月1日北京市12 408辆出租车的GPS数据，每条数据包含了车辆标识、纬度、经度、海拔等信息，对于时间快照的粒度，本文设置为1 min，选取经纬度信息进行试验。由于该数据集收集的仅为移动物体的信息，为了能够实现对混合数据的处理，需要对数据集进行一些处理，生成静态型数据，其过程如下：1)读取数据集中的移动型数据的信息；2)随机选取一些移动型数据；3)筛选出这些移动型数据的经纬度属性信息；4)将这些刚开始移动时的经纬度信息作为其整个聚类过程的经纬度信息，不再发生变化，以代表静态型数据。将这样处理过后的数据作为实验所用的混合数据。

此外，为对比算法性能，构造一组人工模拟数据集。人工模拟数据集的构造过程如下：1)在二维空间[0,l]×[0,l]，随机生成一组ns个静态数据；2)在二维空间中随机添加nm个移动数据，并记录下这时的二维空间中数据的位置分布，然后删除移动数据；3)重复步骤2)n次，以模仿移动数据的移动状态和采集n次时间快照数据。

经过以上步骤，在二维空间[0,l]×[0,l]中构造一个包含nsnm个混合数据集。

首先使用真实数据集进行实验，将数据集中的出租车抽象为二维数据点，随机选择在数量上相等的移动型数据与静态型数据，作为混合数据集，其中静态型数据从移动数据转化而来。实验参数设置为：邻域参数ε设置为100 m，MinPts=5，时间阈值kt=5 min，距离阈值δ=1 000 m。从真实数据集中随机选取5组出租车24h的运行时间快照，这5组数据分别是2 000,4 000,6 000,8 000,10 000，其中每组数据由50%的移动型数据和50%的静态型数据组成。然后各算法运行100次，取各算法的最短运行时间和最好的F指标值以及S指标值，如图3、表1、表2所示。

图3 运行时间对比图Fig.3 Comparison of running time

从各算法的运行时间对比中，本文所提算法MMPSP算法和其他算法相比，运行时间要高于SDPC算法与TAD算法，但没有高出很多。原因是MMPSP算法在识别数据的聚类方面，需要先分别对静态型数据和移动型数据进行聚类处理形成聚类簇，然后再判断形成移动簇与静态簇，是否形成混合簇。通过观察表1的F指标值数据对比表与表2的S指标值数据对比表，得出本文所提算法要好于只处理一种状态类型的聚类算法，因为在本文的混合数据中移动数据与静态数据各占一半，而SDPC算法与TAD算法只能识别出其中一半类型的数据，另一半类型数据无法进行识别和聚类处理，所以聚类效果较差，得到的各个指标值低于本文所提算法。

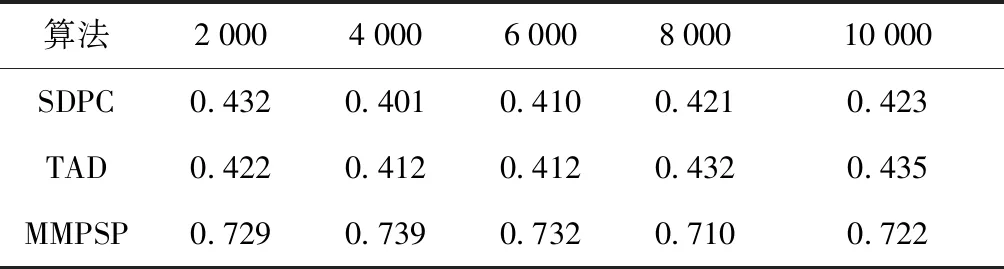
表1 真实数据集F指标值对比表Tab.1 Comparison of real dataset F indicator values

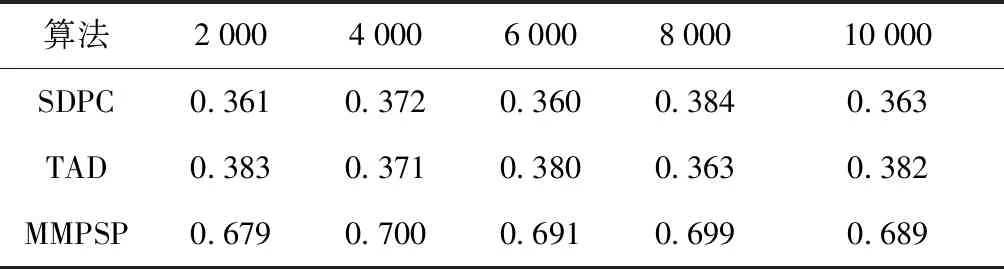
表2 真实数据集S指标值对比表Tab.2 Comparison of real dataset S indicator values

再使用人工模拟生成仿真混合数据集进行实验，仿真混合数据包含1 000张时间快照的数据，一共有5组数据，每组有1 000，2 000，3 000，4 000，5 000的数据量，并且移动型数据与静态型数据各占50%，测试仿真混合数据与真实数据集对聚类效果的评价标准相同，也是从F指标与S指标等方面进行实验对比。从图4的仿真数据运行时间对比图，可以得出与真实数据相似的结论，即本文所提算法运行时间要略高于对比实验算法。从表3的F指标值对比表和表4的S指标值对比表，也可以看出本文所提算法相对于只能处理一种数据类型的算法，聚类效果要好一些。

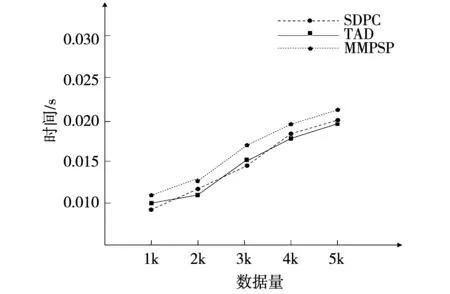
图4 人工仿真数据运行时间对比图Fig.4 Simulation data running time comparison chart

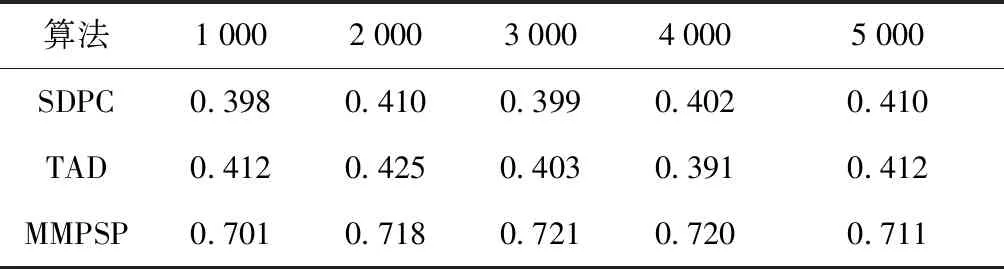
表3 仿真数据F指标值对比表Tab.3 Comparison of simulation data F indicator values

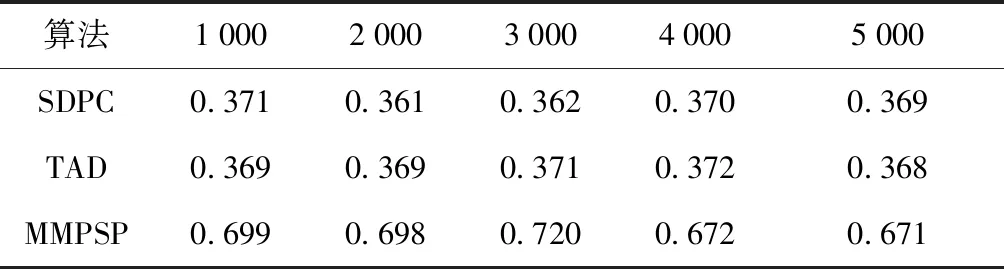
表4 仿真数据S指标值对比表Tab.4 Comparison of simulation data S indicator values

在前述实验中，显示出了本文所提MMPSP算法比只能处理单一类型数据的算法，在处理混合数据时取得的聚类效果要好。在实验开始处已经提到目前还没有针对混合数据进行聚类处理的研究，为了进一步证明MMPSP算法的合理性和有效性，本文提出一个新的可以处理混合数据的实验算法RG算法进行对比实验，该算法由一个处理静态数据的算法RNN-DBSCAN[20]算法和一个处理移动数据的算法GR+[10]构成。在实验过程中，每张时间快照内的静态型数据使用RDD-DBSCAN算法处理，移动型数据则使用GR+方法进行处理。

此外，为更好的衡量聚类效果，增加一个聚类评价指标，即聚类精度Accuracy。

在真实数据集上进行实验，实验参数设置与之前相同。选取5组数据进行对比实验，实验数据信息与前述的真实数据实验数据信息相同，为避免冗余，不再赘述。将这5组数据分别进行多次实验，取MMPSP算法与RG算法的最好聚类结果进行比较。为更加清晰地对比实验结果，将各指标值列于同一个表格中，如表5～8所示。表5～8展示了MMPSP算法与RG算法在不同的数据量下F指标值，S指标值和聚类精度Acc的对比结果。通过观察可以发现，随着数据的增多，本文所提MMPSP算法与RG算法不论是在F值、S值以及聚类精度Acc值方面都基本趋于稳定。在F值方面，MMPSP算法稳定在71%～74%，RG算法则稳定在70%～73%，具体到每组数据时，MMPSP算法均高于RG算法。S值方面，MMPSP算法大致稳定在67.9%～70.0%，RG算法则大致稳定在65.1%～68.0%，在每组数据对比下，MMPSP算法要高于RG算法。在Acc值上也呈现出与F值和S值相同的情况。结合表8的时间可知，虽然本文所提MMPSP算法时间消耗上要略高于RG算法，这是因为MMPSP算法需要处理不同类型数据之间的关系，所以导致时间消耗略有升高。虽然时间上消耗要多一些，但是在聚类效果上好于RG算法。

表5 真实数据集F指标对比Tab.5 Comparison of real dataset indicator

表6 真实数据集S指标对比Tab.6 Comparison of real dataset S indicator

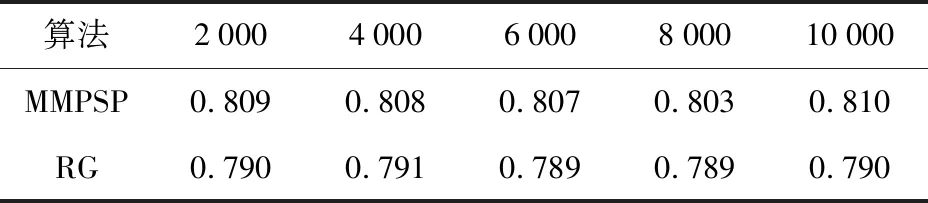
表7 真实数据集多组数据各指标对比Tab.7 Comparison of real dataset Acc indicator

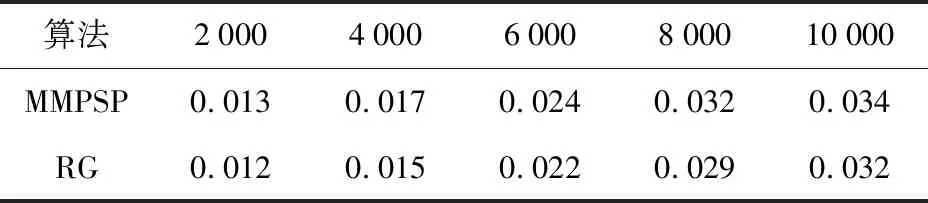
表8 真实数据集耗时(秒)对比Tab.8 Comparison of real dataset time(s) indicator

综上所述，本文所提MMPSP算法与只能处理单一数据类型的SDPC算法与TAD算法进行了多组实验对比，显示出了MMPSP算法可以有效针对混合数据进行处理。为进一步证明本文所提算法的合理性和有效性，提出了对比实验算法RG算法。此外，增加新的聚类评价指标聚类精度Acc值，多方面衡量聚类效果，实验结果表明，本文所提算法对混合数据的聚类处理具有良好的效果。

4 结 语

现有的聚类算法对单一数据类型的数据进行聚类处理可以得到良好的聚类效果和准确率，对混合数据类型的聚类效果则较差。本文通过对包含移动型数据与静态型数据的混合数据的分析和讨论，提出MMPSP算法，并通过实验证明其处理混合数据的聚类时具有良好的效果。但时间复杂度略高，下一步将从寻求既可以有效记录数据信息，又不会导致时间复杂度升高进行优化。