基于小波包全频带分析和OS-ELM的小电流单相接地故障选线

嵇文路，赵晓龙，张 明，杨红磊，翁嘉明

(1.国网江苏省电力有限公司 南京供电分公司，南京 210019；2.中国电力科学研究院有限公司，北京 100192；3.上海交通大学 电力传输与功率变换控制教育部重点实验室，上海 200240)

0 引 言

我国配电网具有点多面广的特点，配网故障也以单相接地故障为主[1]，然而在小电流接地系统发生单相接地故障时，由于中性点接地方式与大电网的不同，产生的短路电流信号微弱，不利于准确可靠地检测出故障线路，如何提高小电流单相接地故障选线的成功率，对配网可靠运行具有重要意义。

目前，国内外学者已开展的传统单相接地故障研究方法主要包括基于暂态零序电流突变信号、能量信号、幅值信号的方法等[2-4]。文[5]用小波变换的方法提取故障后的行波信息，构造判据以实现故障线路的判定。文[6]利用小波变换的方法提取出各馈线零序电流的暂态量，通过比较电流极性实现故障选线。在配电网单相接地故障中，由于暂态信号受到过渡电阻等多种噪声因素的干扰，易造成误选的情况，严重影响了算法的准确性。由于小波变换具有对信号局部提取和滤除噪声信号的良好性能，因此更适应于暂态信号杂乱、故障状态复杂的配网单相接地故障分析[7]。

在配电网单相接地故障分析中，具有分布并行处理、非线性映射、自适应学习和鲁棒容错等特性的神经网络方法尤为适用。国内外学者利用不同的神经网络分析方法，开展了小电流单相接地故障选线分析的研究，并取得了显著进展[8]。传统的神经网络分析方法存在学习速度慢、泛化能力不强、易陷入局部最优等缺陷，文[9]提出一种新型单隐层前馈神经网络算法，称为极限学习机(extreme learning machine, ELM)，其具有学习速度快、泛化性能优良等特点，已被应用于电力系统优化分析求解当中。在ELM基础上，文[10]提出了一种在线序贯ELM(online sequential-ELM, OS-ELM)算法，其特点是历史数据分批进行训练并且支持可变化的样本数，每一轮训练过程中训练算法仅输入当前批次数据并更新网络权值，无需重复扫描历史数据，使得该方法具有更强的泛化能力。考虑到实际配电网单相接地故障选线系统中所有的数据可能不是一次性添加到网络中，且实际配网数据存在错误或缺失，因此OS-ELM算法更能满足配电网单相故障接地选线的需要。基于极限学习机的众多优点，本文提出了一种小波包全频带分析和OS-ELM相结合的配电网单相接地故障选线新方法。

2 单相接地故障特征提取

2.1 配电网单相接地故障暂态分析

谐振接地配电网发生单相接地故障时，非故障相电压升高，故障相电压降低，故障相电容通过故障线路向故障点放电，由于线路具有分布电容和电感参数，使得故障电流具有衰减震荡特性[11]。暂态电容电流是由故障相电压突然降低而引起的放电电流和非故障相电压突然升高而引起的充电电容电流之和。在故障点有两个暂态分量电流流过，其中暂态电容电流衰减较快，暂态电感电流衰减较慢。流过。配电网谐振接地系统模型如图1所示，由文[12]知故障接地电流表达式为：

id=(ICm-ILm)cos(ωt+φ)+ICm[(ωfsinφsinωt)/ω-

cosφcosωft]e-t/τC+ILmcosφe-t/τL

(1)

式中：ICm为电容电流稳态幅值；ωf为暂态自由分量振荡分量的角频率；τC为电容回路的时间常数；ILm为电感电流的稳态值；τL为电感回路的时间常数。

图1 10 kV 谐振接地系统模型Fig.1 Model of a 10 kV resonant grounding system

故障暂态能量主要集中在故障零序电流的首半波，因此故障信息主要从故障后首半波获得。故障发生瞬间，零序电流的暂态特征明显，但持续时间较短。暂态电流大小在很大程度上取决于暂态电容电流的大小，频率大小亦是如此。其幅值跟初始相位角相关，故障出现在相电压处在峰值时刻时，暂态电容电流幅值达到最大值，而故障出现在相电压处在过零位置时，暂态电容幅值很小，衰减直流分量幅值、能量较大。

2.2 基于小波包全频带分析的故障特征提取

在谐振接地配电网的单相接地故障中，其故障信号的暂态特征受故障发生时刻、接地点过度阻抗、线路参数等随机条件的影响很大。为反映故障条件的随机性及其对故障暂态信号特征的影响，利用小波包良好的时频局部化能力与能量无损性特点，对故障暂态电流信号做小波包全频带分析。

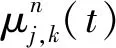
(2)

式中：n=0,1,2,…为振荡参数，j∈Z和k∈Z分别是尺度参数和平移参数。

当n=0,1;j=k=0时，初始的2个小波包函数定义为

μ0(t)=φ(t),μ1(t)=ψ(t)

(3)

式中：φ(t)和ψ(t)分别是正交尺度函数和正交小波函数。初始小波函数满足以下双尺度方程：

(4)

式中：h(t)和g(t)分别为对应的多尺度分析中低通滤波系数和高通滤波系数。则当n=2,3…时，其他的小波包函数满足：

(5)

那么，由式(5)所决定的函数集合{μn(t)},n=0,1,2,…，就称为关于正交尺度函数φ(t)的小波包。对于一组离散信号x(t)，小波包分解重构算法如式(6)和式(7)：

(6)

(7)

利用上述小波包过程进行单相接地故障特征提取，对各线路零序电流进行小波包分解。第i个频带对应的能量值为

(8)

通过对暂态信号的故障特征的分析可知:

在电压相角φ=0附近发生任意过渡电阻大小的接地故障和在任意电压相角大小发生过渡电阻较大的接地故障两种情况下，各线路的零序暂态信号能量集中频带都是在低频带上。因此可以统一在低频带上按照各线路暂态信号的能量大小来确定故障选线。在低频带上，故障线路所具有的能量要大于其他线路所具有的能量值。

在电压相角φ=π/2附近发生过渡电阻较小的单相接地故障情况下，各线路能量集中的频带可能不同，能量集中的频带也可能有多个，依特征频带选线较困难，但此时过渡电阻较小，暂态零序电流的幅值较大，谐波的五次分量相对也较大。因此，可以按照各线路暂态信号在五次谐波所在频带的能量大小来判别出故障线路。

因为故障接地线路的暂态零序电流信号的幅值为系统网络内的其他所有健全线路的暂态零序电流信号的幅值总和，零序暂态信号在各频带的信号能量表示为小波包系数的平方和，所以，综合考虑各线路在全频带上的能量统计和分布特性，在绝大多数子频带上满足故障线路所具有的能量大于其他线路所具有的能量值。

据此，定义线路Li在(j,k)频带上的故障权重因子为：

(9)

其中：N为线路的总条数；j为小波包的分解层数；Ei,(j,k)为线路在(j,k)子频带上所具有的能量；E(j,k)为所有线路在(j,k)子频带上所具有的能量总和。

在式(9)的基础上，定义Li线路的综合全频带故障权重因子为

(10)

其中：Ci为线路Li在所有的子频带当中故障权重因子为最大的子频带的个数；C为子频带的总个数。

故障权重因子的大小反映了各线路的故障的可能性大小，故障线路的故障权重因子大于健全线路的故障权重因子，据此可以作为选线的判据。

3 OS-ELM理论

与传统神经网络参数调整机制不同，在极限学习机理论中，由线性方程求解出参数权值，进而随机生成权值、偏差等隐层学习参数。这使得极端学习机的训练速度、泛化性能均较传统神经网络法有大幅提升。

在线序贯极限学习机算法对于单隐层神经网络输出权重的学习过程主要分为两个部分，第一部分为初始步骤，通过少量样本得到单隐层前馈神经网络的输出权重β，第二部分为在线学习步骤，即利用单个样本或样本数据块更新在初始阶段学习到的单隐层前馈神经网络的输出权重β。

3.1 初始化阶段

(11)

随机生成输入层与隐藏层的连接权值wj和隐含层阈值bj，βj为是连接第j个隐层神经元和输出神经元的权值。

(12)

已知目标输出：

(13)

计算初始权值β0也就是计算‖H0β-T0‖最小值问题。

常规条件下，隐层节点数目比起训练样本数目可以忽略，即N0>>L，此时H0是非方阵，根据广义逆引理，上述线性系统的最小范数最小二乘解为

β0=H†T0

(14)

(15)

3.2 在线学习阶段

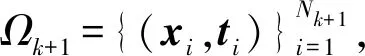
(16)

式中Tk+1=[t1,…,tNk+1]T。

当逐个获得训练数据时，Nk+1=1，式(16)由如下简化形式：

(17)

式中hk=[G(w1,b1,xk+1),…,G(wL,bL,xk+1)]。

4 小波包全频带分析和OS-ELM故障诊断

在某些故障情况(故障时电压初相角在峰值附近且故障接地电阻较小的情况)下，各线路的特征频带不同，能量较集中的频带也不止一个，此时如果仅仅依靠各线路在其特征频带上的故障特征信息进行选线，就不能有效的利用该线路的暂态故障特征，甚至会出现误判的情况(健全线路在其特征频带上的能量大于故障线路，健全线路的小波包系数模极大值大于故障线路)，降低了选线的可靠性；实际配电网单相接地故障选线问题中，仍存在数据非一次性添加、实际配网数据存在错误或缺失等问题。针对小波选线存在的上述问题，论文给出一种小波包全频带分析和OS-ELM网络相结合的故障选线新方法。

先用小波包对暂态零序电流进行适当频带宽度的分解，然后分别计算各线路在低频带(4,0)、五次谐波所在频带(4,1)、综合全频带上的故障权重因子作为各线路的故障表征值构造故障特征向量Z，再将Z输入到OS-ELM神经网络进行智能融合，输出一个由各线路的故障权重因子构成的故障特征向量T，综合故障权重因子最大的线路即为故障线路；同时在线选线得到的在线样本更新到样本集中，更新OS-ELM神经网络的输出权值。该方法综合利用了全频带的故障信息，可有效地解决小波选线存在的能量集中频带不同引起误判的问题；利用了选线系统的历史信息和在线信息，提高了故障选线算法的鲁棒性，流程图如图2所示。

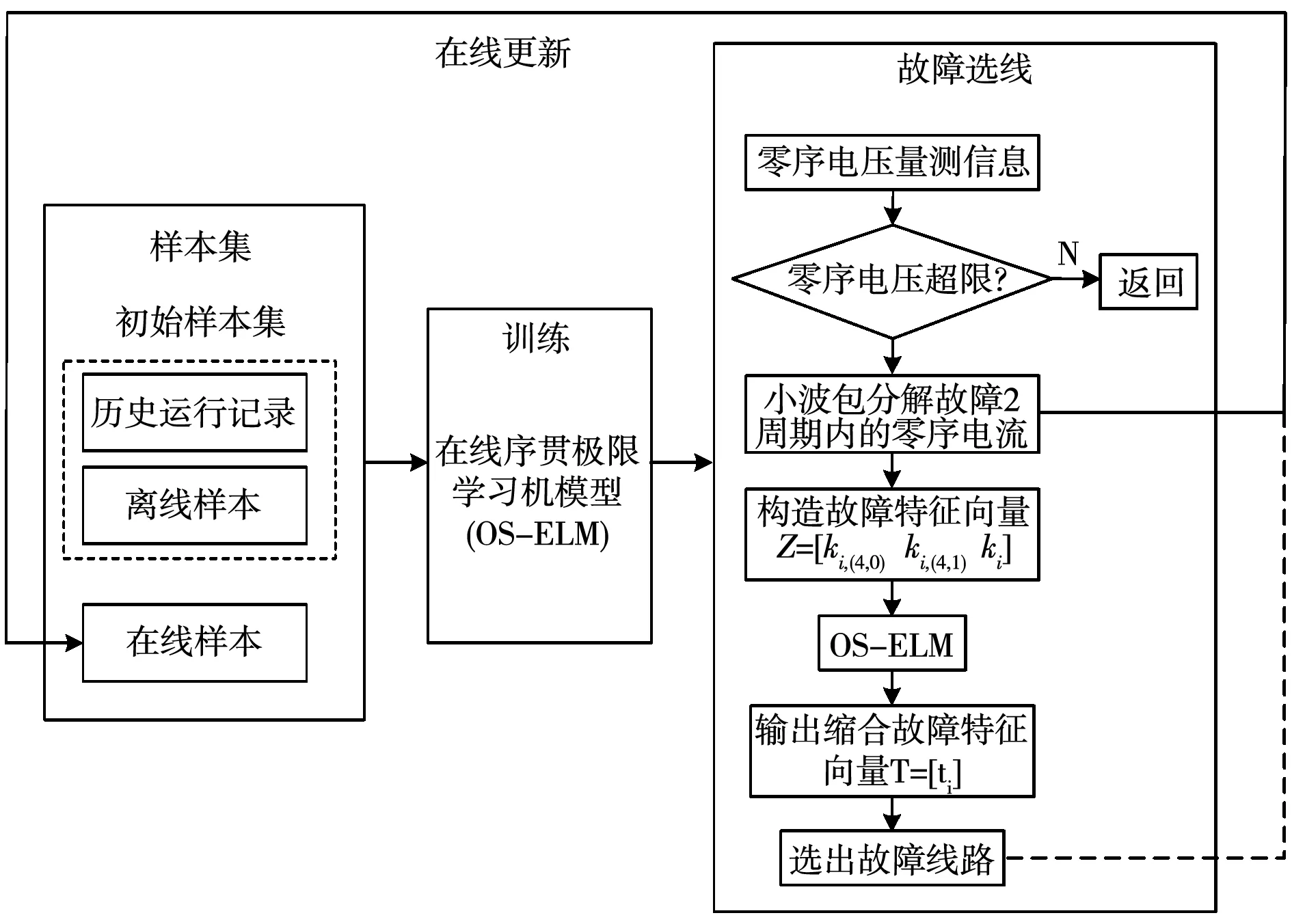
图2 小波在线序贯极限学习机诊断流程图Fig.2 Diagnosis flow chart of wavelet OS-ELM

5 诊断实例

5.1 仿真模型

利用MATLAB软件搭建图1消弧线圈接地配电网系统的故障选线的仿真模型，如图3所示。

图3 仿真模型Fig.3 Simulation model

该配电仿真系统具有4条主馈线，架空线路长度分别为L1=8 km，L2=10 km，电缆线路长度为L3=5 km，L4=3 km架空线路、电缆线路参数如表1所示。消弧线圈接地系统的补偿度设为p=10%，由线路参数求出系统对地分布电容C∑，进而计算出消弧线圈等效电感L=(1/1.1)×1/(3ω2C∑)=0.742 1 H。

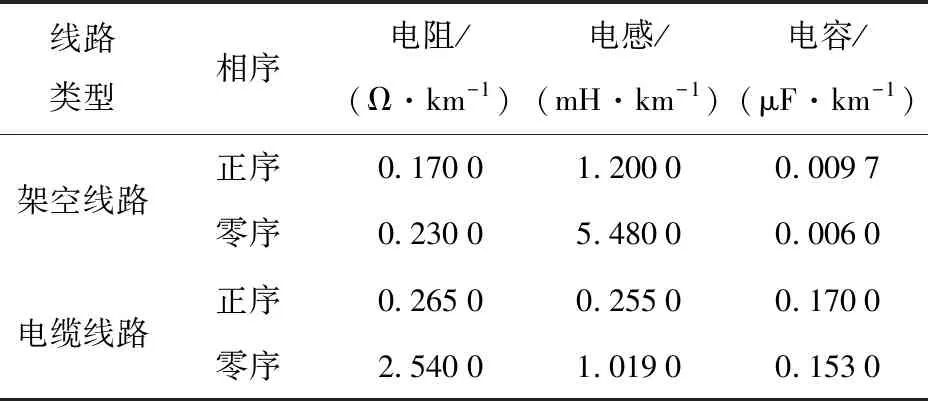
表1 线路参数Tab.1 Line Parameters

利用上述建立的10 kV接地配电网系统的故障选线的仿真模型，分别对4条线路在电压初相角为0°、15°、30°、45°、60°、75°、90°，故障位置为线路距离母线的15%、30%、45%、60%、75%、90%长度处，过渡电阻为0 Ω、20 Ω、100 Ω、500 Ω、1 000 Ω、3 000 Ω时的不同故障情况做单相接地仿真试验，总共得到4×7×6×6=1 008组样本，随机选取600组样本进行训练样，其中300组用于初始化阶段训练样本，300个进行增量学习，剩余408组样本作为测试样本。

本文选取dB10小波包来分析，信号的采样频率取为4 kHz，即有效频率为2 kHz，选线的频带宽度定为125 Hz，即分解的层数为4层，暂态信号分解为24=16个子频带，其中(4,0)代表0～150 Hz频带，(4,1)代表125～250 Hz频带，即五次谐波所在频带，以此类推，(4,15)代表1 875～2 000 Hz频带。

5.2 实例分析

5.2.1 故障合闸角为0°时的仿真验证

算例1：线路L4故障，故障合闸角0°，过渡电阻20 Ω，故障点距离母线80%长度处。

系统发生上述条件下的单相接地故障后，仿真可得线路L1～L4的零序电流的波形，如图4所示。

图4 各线路零序电流波形Fig.4 The zero sequence current waveform of each line

将暂态零序电流信号经dB10小波包4层分解后，可按照式(8)计算得到线路L1～L4的暂态零序电流信号在各子频带上的能量比，如图5所示。图中横轴坐标表示子频带的编号，纵轴坐标表示小波包分解在各子频带的能量所占所有频带总能量的比值。

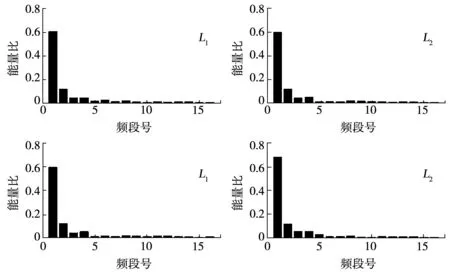
图5 暂态零序电流频谱能量分布图Fig.5 Transient zero-sequence current spectrum energy distribution

由图5可知，线路L1～L4的特征频带相同，均为(4,0)频带，线路L1～L4在特征频带上的能量比大约都在60%左右，因此，线路L1～L4的暂态零序电流的主要故障特征都集中在低频带0～50 Hz范围。利用式(9)计算线路L1～L4在16个子频带上的故障权重因子，如图6所示。图中的横轴坐标表示4条线路的编号，纵轴坐标表示故障权重因子的大小。

图6 各子频带的故障权重因子分布图Fig.6 Fault weighting factor distribution for each subband

由图6可知，在14个子频带上满足线路L4的故障权重因子最大，其中包括频带(4,0)和频带(4,1)。按本文故障选线算法，首先计算线路L1～L4在低频带的故障权重因子(4,0)，五次谐波所在频带的故障权重因子(4,1)，以及综合全频带的故障权重因子，见表2。

表2 各线路的故障权重因子Tab.2 The fault weight factor of each line

由表2可知，线路L4在特征频带(4,0)、频带(4,1)和综合全频带上的故障权重因子均大于其他线路，因此，初步判断线路L4为故障线路。然后将各线路故障权重因子构成的故障特征向量Z=[0.096 4 0.067 8 0.062 5 0.182 6 0.208 5 0 0.241 4 0.275 9 0.062 5 0.479 4 0.447 6 0.875 0]作为输入样本输入到训练好的OS-ELM神经网络进行智能融合，输出融合故障特征向量T=[-0.039 8-0.032 4 0.053 2 1.019 1]。线路L4的综合故障权重因子最大，因此可以判断线路L4为发生故障的线路，判别结果与实际的故障情况相同，选线正确。

5.2.2 故障合闸角为90°时的仿真验证

算例2：线路L1故障，故障合闸角90°，过渡电阻100 Ω，故障点距离母线30%长度处。

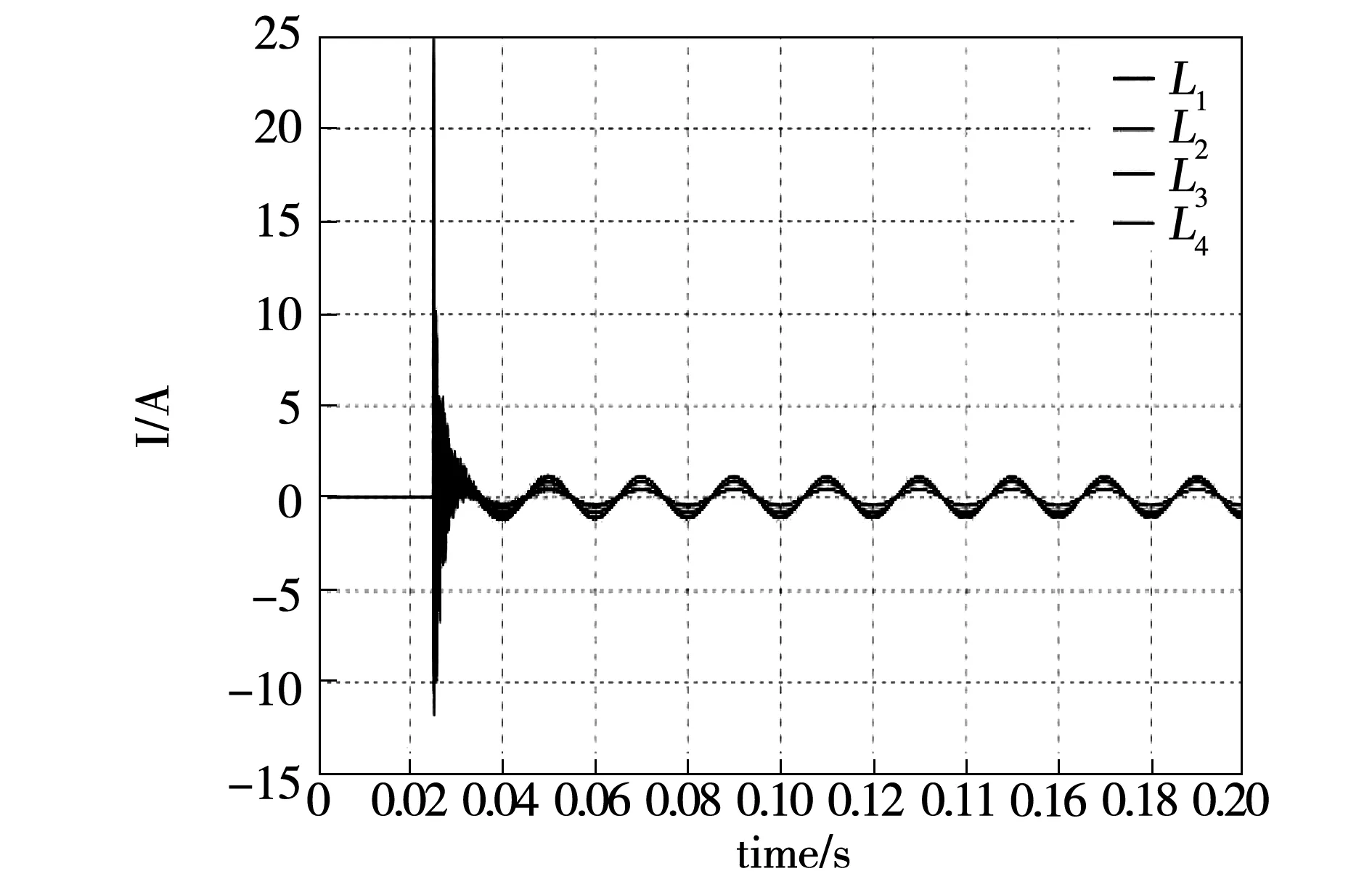
图7 各线路零序电流波形Fig.7 The zero sequence current waveform of each line

图8 暂态零序电流频谱能量分布图Fig.8 Transient zero-sequence current spectrum energy distribution

按照案例1的处理方法，得到暂态零序电流信号小波包分解的能量图和各子频带的故障权重因子分布图，如图6～9。可知，线路L1～L4能量最为集中的特征频带为(4,0)、(4,4)、(4,9)，此时若只利用特征频带(4,0)进行选线，就会出现误判的情况。计算线路L1～L4的故障权重因子，见表3。可知，在频带(4,0)上，线路L2的故障权重因子最大，在频带(4,1)上，线路L1和L2的故障权重因子比较接近，线路L1和L2均可能是发生故障的线路，选线失效。

表3 各线路的故障权重因子Tab.3 The fault weight factor of each line

依本文的故障选线算法，将故障特征向量Z=[0.309 6 0.355 7 0.437 5 0.329 0 0.349 4 0.187 5 0.125 4 0.100 6 0.125 0 0.235 4 0.194 1 0.250 0]作为输入样本输入到训练好的OS-ELM神经网络进行智能融合，输出融合故障特征向量T=[0.693 8 0.341 0-0.054 7 0.020 4]。线路L1的综合故障权重因子最大，因此可以判断线路L1为发生故障的线路，判别结果与实际的故障情况相同，选线正确。

为与在线小波极限学习机的结果进行比较，另外选择BPNN、RBFNN、SVM以及ELM分别对样本进行故障选线，ELM的隐层神经元数目、BPNN的隐层节点数以及RBF的扩展系数取值利用交叉验证方法获得，SVM中核函数为高斯核函数，正则化参数γ及核函数参数σ2通过交叉验证获得，多类分类问题采用1对多方法。

5种方法得到的诊断结果如表4所示。从诊断结果看，OS-ELM和ELM的诊断精度明显高于其他3种方法，且训练时间和测试时间明显少于另外3 种方法，利用OS-ELM进行单相接地故障选线能够取得精度最高的结果，且由于其需要人工干预参数只有一个，通过求解线性方程的方式获得输出权值，相比其他3种方法，更适合将其用于在线故障诊断，这也是下一步需要研究的内容。

表4 5种方法诊断结果Tab.4 Diagnosis results for five methods

6 结 论

本文选取dB10小波包对故障信号进行多分辨率分析，综合考虑故障暂态信号特征在全频带上的表征情况，使用故障权重因子评价了各线路故障信号特征，进行单相接地故障选线；针对传统人工智能方法在进行单相接地故障选线时存在训练时间过长、人工参与调节参数过多等问题，将在线序贯极限学习机(OS-ELM)引入故障选线中，提出了一种小波包和线序贯极限学习机结合的诊断方法。该方法有效地解决了传统基于小波分析的故障选线方法存在的各线路能量集中频带不同导致选线困难或失效的问题，选线准确性高。仿真结果表明，提出的小波在线序贯极端学习机单相接地故障诊断精度达96.76%，而仿真用时在5 ms之内，比 3种传统常用故障诊断方法有更高的速度和准确性。鉴于其良好的性能，下一步将利用其开展实际单相接地故障系统中的在线故障选线相关研究。