地铁轮对复合故障对车辆动力学性能的影响*

2021-05-21 01:54崔晓飞姚德臣杨建伟夏志成陈小英

铁道机车车辆 2021年2期

崔晓飞，姚德臣，杨建伟，夏志成，陈小英

（1 北京建筑大学机电与车辆工程学院，北京100044；2 北京建筑大学城市轨道交通车辆服役性能保障北京市重点实验室，北京100044；3 北京锦鸿希电信息技术股份有限公司，北京100071）

如今，地铁正逐渐成为人们理想的日常出行方式，给人们带来舒适、快捷、方便的同时，地铁车辆也在发生损伤，这些损伤不仅造成了振动冲击的加剧，还会大大缩短车辆的使用寿命，甚至危害行车安全。例如，地铁车辆车轮在运行中发生的沟槽、擦伤、剥离、扁疤和多边形等异常磨耗现象，这些异常磨耗致使车辆产生轮轨匹配关系恶化，车辆动力学性能降低，维修运营费用增加等众多不利影响，给地铁正常运行带来巨大的挑战［1-2］。

国内外对轮对踏面磨耗影响车辆动力学性能的研究成果显著。黄育斌等［3］建立地铁车型的动力学模型，仿真发现车轮踏面异常磨耗使轮轨接触点分布改变，对车辆动力学性能降低明显。张合吉等［4］建立了车轮/辙叉接触有限元模型，分析结果表明车轮踏面出现的凸台异常磨耗使轮轨接触应力增大，对车轮辙叉接触不利。胡志柯等［5］利用多体动力学分析软件UM 建立地铁拖车模型，分析发现椭圆轮对不仅使轮轨力增大，同时磨耗率也大于标准轮对。孙宇等［6］基于车辆—轨道耦合动力学理论，分析认为高速动车轮对的凹形磨耗会增大轮轨横向力的振动幅值，不利于行车安全。宋志坤等［7］通过建立柔性轮对的车辆动力学模型，研究认为车轮多边形引起轮轨垂向力较大的波动，并受多边形幅值和阶数的影响。综上，轮对踏面磨耗故障对车辆动力学性能的影响不容小觑，对这方面不断进行深入的分析具有重要现实意义，而以往研究中多是考虑轮对所产生的一种异常磨耗故障对车辆动力学性能的影响，由于受线路和车辆等因素的影响，轮对产生的异常磨耗具有随机性和难以预测性。另外，实际检测中对于待旋修的轮对经常会有多种故障存在的问题，因此要考虑轮对踏面产生复合故障的情况下，对车辆动力学性能所产生的影响。

文中针对地铁车辆利用多体动力学仿真软件SIMPACK 构建车辆动力学分析模型，由于多边形与沟槽（尤其是拖车）两种异常磨耗普遍存在于地铁车辆中［8-9］，故这里选取多边形化和沟槽这两种故障作为轮对踏面的复合故障，并仅施加于车辆模型的一位轮对踏面上，根据试验结果，分析LM型标准踏面、单一故障踏面以及复合故障踏面使地铁车辆动力学性能产生的变化。

1 模型建立

1.1 动力学模型

在开始建立整车前，构建拓扑结构图是利用SIMPACK 软件仿真分析必不可少的环节，拓扑图可以清晰描述出模型中部件的数目、相互作用的力元类型及参考界面等，并反映出各物体之间相互连接的关系，如图1 所示。

图1 车辆系统动力学模型拓扑图

根据系统拓扑结构建立某型地铁车辆拖车动力学模型，模型中主要由1 个车体、2 个转向架、4组轮对、8 个轴箱以及一系悬挂、二系悬挂等组成，整个车辆系统一共包含50 个自由度，地铁车辆整车模型如图2 所示，其主要参数见表1。其中车辆主要部件例如车体、轮对等的弹性变形相比悬挂装置很小，故均视为刚体［10］，一系悬挂采用圆锥橡胶弹簧，二系悬挂采用空气弹簧并配有垂向、横向减振器以及横向止档等装置，轮对采用地铁车辆上广泛应用的LM 磨耗型踏面，车轮名义滚动圆半径为420 mm，钢轨踏面选用60 kg/m 的标准截面钢轨，轨距为1 435 mm，轨底坡1∶40。

1.2 模型验证

由于铁路车辆的轮对踏面本身具有一定斜度，其在直线轨道上滚动前进的同时还会产生一定的横向位移，这种运动形式称为蛇行运动，随着运行速度的提高轮对产生的横向移动逐渐增大，当速度达到某一数值时，轮对左右摆动幅度过大以至于车辆不能够稳定运行，出现蛇行失稳的现象，对应这一速度值可用非线性临界速度来衡量［11］。在车辆系统模型建立完成后，应首先对车辆的非线性临界速度进行验证，该速度应该大于车辆设计的最高运行速度，以保证车辆稳定运行。

文中测量非线性临界速度值采用的是减加速度法，即开始时在轨道上施加一段不平顺，使车辆振动起来，再以较高的运行速度及恒定减加速度作用下在无不平顺的直线轨道上运行，通过观察轮对横移量收敛情况来判断非线性临界速度的大小［12］。车辆非线性临界速度的测量结果如图3 所示，轮对横移量收敛于速度为114 km/h 的点，文中所建立的地铁车辆设计最高运行速度为80 km/h，临界速度须在此基础上留有一定余量，此时非线性临界速度值高于最高运行速度40%，故能够满足车辆稳定运行的条件［13］。

图2 车辆系统动力学模型

表1 地铁车辆主要参数

1.3 轮对踏面处理

地铁车辆在运行过程中所产生的复杂轮轨相互作用，使轮对踏面不能保持初始外形而不断磨损，甚至会产生异常磨耗情况。例如，在拖车车轮上频繁采用空气制动后，闸瓦与踏面的接触表面就容易产生沟槽异常磨耗［14-15］，依据实测沟槽踏面参数，对其进行拟合，得到了深度约为2 mm 的沟槽故障踏面，沟槽踏面外形及其轮轨接触关系如图4 所示，此时，车轮踏面与60 kg 钢轨匹配的轮轨接触几何关系产生了明显的变化，在发生沟槽位置处轮轨之间出现了2 点接触，这势必会对车辆动力学性能产生不小的影响。

图3 车辆非线性临界速度

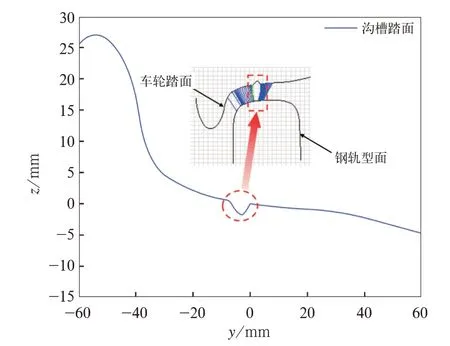
图4 沟槽下的车轮踏面与轮轨接触

受线路条件、车辆结构等因素的影响，轨道车辆的车轮还经常会产生多边形异常磨耗情况［7］，车轮多边形是由车轮圆周方向发生的不均匀磨耗造成的，也称为车轮谐波磨耗或车轮周期性非圆化，具有一定的阶数和波深。在SIMPACK 中采用简谐波函数来描述多边形车轮的变化趋势，使车轮半径实现周期性的变化，见式（1）：

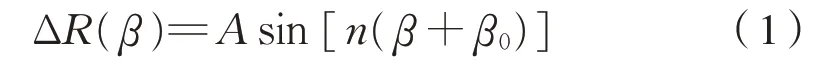
式中：ΔR为轮径差，mm；β为车轮旋转角度，rad；β0为初始相位偏移量，rad；A为多边形波深，mm；n为车轮多边形阶数。

根据文献中地铁车辆实测数据下车轮多边形参数［16-18］，设置谐波阶数为9，波深为0.08 mm 的车轮多边形故障，此时踏面圆周状态可拟合为如图5 所示。

图5 车轮踏面圆周状态

最后，将沟槽踏面数据导入一位轮对中，并以此踏面为基础对其设置多边形故障，从而实现车辆在线路上运行过程中沟槽踏面车轮的半径同时发生着周期性变化，即形成轮对的复合故障踏面，分析其引起车辆动力学性能的变化趋势。

2 结果分析

2.1 平稳性分析

地铁车辆运行过程中受车辆自身部件结构以及轨道线路不平顺等激扰作用，会产生各种振动，影响乘客的乘坐舒适感，评价车辆乘坐舒适性最直接的指标就是车体的振动加速度［19］。根据地铁的线路条件，轨道不平顺激励的输入可采用德国高干扰轨道谱［10，20］。文中对车辆系统模型设置恒定速度为50 km/h，在车体前端转向架中心一侧1 m处设置传感器，测量此时车体的横向和垂向振动加速度随时间历程的变化情况，并统计得到其有效值如图6 所示，垂向振动加速度的有效值呈现复合故障＞多边形＞沟槽＞LM 踏面的状态，在横向振动加速度中沟槽踏面的横向振动要比多边形踏面更强，且复合故障踏面在横向上的有效值仍是最大的，可见踏面上2 种故障复合后可使车体振动加速度叠加，并较单一故障时更大。

由于复合故障踏面使车体的振动加速度在垂向和横向上均增大，且加速度值具有叠加效应，如图7 所示，对比复合故障和单一故障输出的振动加速度的时间历程，也可以明显看出2 种故障对车体振动的影响是不一样的，沟槽踏面在横向振动中与复合故障的重合度更高，多边形踏面在垂向振动中与复合故障踏面的重合度更高。可见，车轮踏面的沟槽故障引起的轮轨接触状态的转变主要是对车体的横向振动产生影响，而多边形故障的车轮踏面会产生较大的轮轨冲击，故对车体的垂向振动影响更大。

按照GB/T 5599-1985《铁道车辆动力学性能评定和试验鉴定规范》中规定，为更准确的评价车辆的运行平稳性，还应考虑振动加速度的频率。于是，用平稳性指标来评价车辆运行性能得到广泛应用［19］，在我国一般可采用Sperling 指标评价客车车辆的运行平稳性。

Sperling 指标Ws可以表示为式（2）：

工程教育的发展必须以产业需求为导向才能具有持久的生命力，产教融合这一育人模式能够有效将产业发展与人才培养相结合，是未来高等教育发展的重要支撑。在建设新工科的大背景下，产教融合面临着新的挑战，主要是来自产业转型升级对学科专业布局的挑战、高校与企业融合度急需加深的挑战以及政府行业协会等第三方加强协调指导的挑战。这些挑战也是促使产教融合深入发展的机遇，因此，应当迎难而上，抓住机会，构建新时期的产教融合育人新模式。

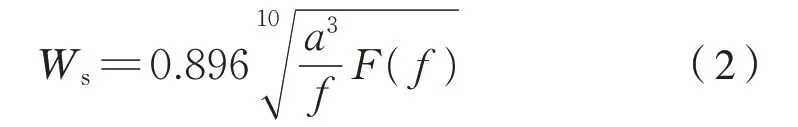
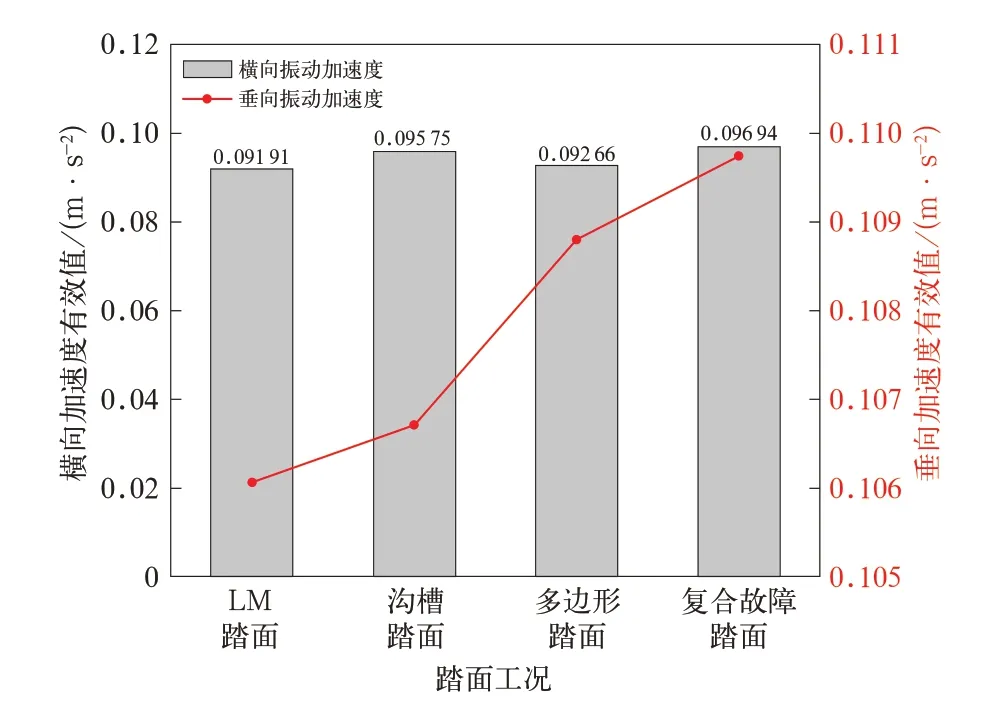
图6 振动加速度有效值

图7 振动加速度时间历程

式中：a为车体振动加速度，cm/s2；f为振动频率，Hz；F(f)为考虑人体对各种频率振动敏感程度的修正系数。垂向和横向平稳性采用相同评定等级，当Ws≤2.5 为优秀等级、Ws≤2.75 为良好等级、Ws≤3.0 为合格等级。我国新造客车的运行平稳性要求应不低于2 级标准，即横向和垂向平稳性指标应不大于2.75。

在测量平稳性指标时，先对50 km/h 的振动加速度数据进行处理得到平稳性指标，再使车辆系统模型以地铁列车常见的运营速度60 km/h 和70 km/h 通过直线线路，统计得到的车体平稳性指标值见表2，根据表中数据分析，各轮对踏面工况的平稳性指标值都随着速度的增加而逐渐增大，且均小于2.5，处于优级范围内，但数值上具有一定差异，沟槽踏面在不同速度下的横向平稳性指标相比LM 踏面时增加明显，这与以上分析的振动加速度情况相吻合，且在速度为50 km/h 时与LM踏面横向平稳性指标的差值约为0.011，60 km/h约为0.021，到70 km/h 时差值约为0.041，可见随着速度的增大沟槽故障对横向平稳性指标的影响有增大趋势，在复合故障的数据中同样符合此规律，数据显示沟槽踏面对垂向平稳性改变不大；而多边形踏面的表现相反，其对垂向振动平稳性影响更强些，在振动加速度分析中也有体现出来，对比数据发现，其垂向平稳性指标与LM 踏面的差值在速度为50 km/h 时约为0.016，而到70 km/h 时的差值仅约为0.004，可见随着速度的增大多边形故障对垂向平稳性指标影响是逐渐变小的，复合故障数据也同样具有此规律；当2 种单一故障踏面复合后，平稳性指标变化规律能够表现出与单一故障之间的联系，而且数据中的垂向和横向的平稳性指标值均大于其他各踏面工况的值。

综上，结合振动加速度的对比和平稳性指标的变化规律，可以得出轮对踏面所产生的类似复合故障使车辆的横向和垂向振动作用增强，不利于车辆的运行平稳性，且较单一故障的影响更大，同时能体现出单一故障下的某些规律，如：在沟槽故障中，横向平稳性随着速度的增大而更加恶化，在多边形故障中，较高的运行速度对车辆的垂向平稳性影响减弱。

表2 车辆平稳性指标

2.2 安全性分析

车辆通过曲线时，特别经过缓和曲线时，轮轨间会发生非常复杂的作用力，容易造成轮轨磨耗及车辆脱轨等现象的发生［11］，所以分析车辆通过曲线时的动力学性能变化对确保列车运行安全、降低轮轨磨耗有重要意义。根据GB/T 5599-1985规定客运列车常采用脱轨系数、轮重减载率等作为评价车辆运行安全性指标。

脱轨系数为某时刻作用在车轮上的横向力Q和垂向力P的比值（Q/P），脱轨系数的第1 限值1.2 为评定车辆运行安全性的合格标准，第2 限值1.0 为增大了安全裕量的允许标准。

脱轨系数是评价车辆脱轨安全性的最基本指标，但实践表明，轮重减载率过大时也会造成车辆脱轨，因此，轮重减载率作为衡量车轮减载量的重要指标有必要对其进行限定，其限值为式（3）和式（4）：

式中ΔP为轮重减载变化量，kN；为增载和减载侧车轮平均轮重，kN。为方便分析比较，在计算安全性指标时，对脱轨系数及轮重减载率均取最大值。

根据地铁线路特点，文中设置了计算半径分别为300 m、500 m、700 m 以及1 000 m 曲线轨道，并按照GB 50157-2013《地铁设计规范》规定设置超高、缓和曲线长度以及运行速度，测量车辆在上述轨道不平顺下通过这些曲线线路的安全性指标，具体的线路参数，见表3。

表3 曲线线路参数

根据以上线路的设置，测得车辆在不同曲线半径下的安全性指标如图8 所示，图中故障踏面的脱轨系数和轮重减载率在各曲线半径下均大于LM踏面的指标值，且轮重减载率相差较大。其中，沟槽异常磨耗与正常状态的踏面差值较小，对于两种安全性指标均呈一定的恶化趋势；而多边形异常磨耗对轮重减载率的改变是非常明显的，这主要是由于多边形引起强烈的轮轨冲击作用，使得轮轨垂向力相比于正常状态踏面异常增大，从而导致减载率的异常，这同样也可引起脱轨系数的增加；将2 种故障复合后这些趋势也进一步恶化，在各半径曲线中的脱轨系数和轮重减载均达到最大，并且受多边形故障的影响在轮重减载率中也表现出异常增大，不过，此时各工况下的安全性指标均位于限值之内。

综上所述，轮对踏面发生异常磨耗故障会明显降低车辆运行安全性，不同曲线半径线路下，存在多边形故障的踏面对轮重减载率的影响很大，而轮重减载率又是衡量车辆脱轨非常重要的参考指标，所以当轮对踏面形成类似复合故障后，对车辆运行安全性的影响不容小觑。

2.2.2 变速工况

由于地铁运行的线路区间较短，故会存在频繁的加减速运行，而且曲线线路在地铁中的占比可达30%～50%［21］，导致部分曲线线路上也会有车辆的加减速运行，特别是离车站较近的曲线轨道上，车辆在进出站时，不可避免加速或减速通过这些曲线线路，曲线线路上速度的不断变化，将引起车辆重力产生的离心力不断变化，使其与由外轨超高形成的向心力差值也不断变化，就会产生不断变化的未被平衡的力，此时轮轨间的动态相互作用较为复杂。文中设置400 m 计算半径的曲线在变速工况下通过具有轨道不平顺的线路，线路参数见表4。

图8 不同曲线半径的安全性指标

表4 线路参数

在变速工况下，分别设置了加速和减速运行，加速工况下，初始速度为5 m/s（即18 km/h），加速度为1 m/s2；减速工况下，初始速度为22.2 m/s（约为80 km/h），减速度为1 m/s2；2 种工况下车辆运行速度随位移之间的变化过程如图9 所示。

对上述2 种工况进行安全性分析，测量不同踏面状态通过400 m 半径曲线线路的脱轨系数和轮重减载率，测得数据见表5，以及各工况下指标值随时间的变化历程如图10 和图11 所示。加速工况下，各种踏面的轮重减载率最大值发生在出曲线时段，由于加速通过曲线线路，驶出曲线时要经过半径不断变化的缓和曲线，且通过速度也较高，故轮轨之间的相互作用力激烈，导致在此处的指标值比进入曲线时明显增大，脱轨系数的最大值出现在曲线中，距离第二段缓和曲线较近，各踏面的指标变化趋势仍符合上述规律，复合故障踏面的指标值最大，对轮重减载率影响更加明显；在减速工况中，刚进入曲线时的速度较大，驶离曲线时速度低于50 km/h，LM 和沟槽踏面的轮重减载率最大值出现在驶出曲线时段，但受到多边形故障的影响，复合和多边形踏面的轮重减载率最大值出现在进入曲线时速度较高的位置，轮重减载率的变化规律与前述相同，脱轨系数最大值出现在驶出曲线段位置，由于此时运行速度较小，各踏面的指标值重合度也较高，相差很小。对比加减速工况的指标发现，加速工况不同踏面之间的脱轨系数平均增量约为0.004，减速工况约为0.001，加速工况轮重减载率的平均增量约为0.053，而减速工况约为0.024，可见该类故障的轮对踏面加速通过曲线线路对安全性指标的改变要更大。