基于灰色GM(1,1)残差修正模型的动车组故障率预测*

杜文然，陆 航，杨涛存，徐贵红

（1 中国铁道科学研究院 研究生部，北京100081；2 中国铁道科学研究院集团有限公司 机车车辆研究所，北京100081；3 中国铁道科学研究院集团有限公司 电子计算技术研究所，北京100081）

随着我国高速铁路的迅速发展，动车组保有量逐年增多。动车组安全运营是保障铁路安全运营的必要条件之一。对动车组一定周期内的百万公里故障率进行预测，对于宏观掌握动车组运行状态，分析动车组运行安全规律，了解动车组安全裕度具有重要意义。

我国动车组具有大范围跨线开行、运行环境复杂多变等特点。动车组故障的形成是多种复杂因素共同作用的结果，除了设备自身的状态恶化外，还受人为因素、自然因素等多种复杂因素的影响，这些因素有多种多样的表征形式，并且很可能耦合交叉共同作用。在影响动车组百万公里故障率的各种因素中，诸多因素的不确定性较强，难以量化分析。灰色系统理论是处理不确定性半复杂问题的有效方法，在一些影响因素难以定量分析的领域得到了广泛应用［1］。灰色系统理论已成功地应用于医学、图像处理、机器人、工业技术等方面并取得实效［2］。在水上交通运输领域，灰色系统理论被用来预测船舶交通事故，揭示船舶交通事故与其相关影响因素之间的规律性，对船舶交通事故短期预测有较好的效果［3］。在轨道交通领域，采用灰色系统理论预测铁路客、货运量未来发展趋势［4-6］，应用灰色GM（1，1）非等时距修正模型模拟轨道质量指数的趋势成分与波动成分［7］。对于动车组运行故障趋势的预测目前未见相关文献。文中利用灰色理论，以某分析类别动车组百万公里故障数据为原始时间序列，深入挖掘动车组故障数据的特点，研究建立了用于动车组百万公里故障率预测的灰色GM（1，1）残差修正模型。

1 动车组百万公里故障率数据特点

随着中国铁路运营里程的增加，投入运行的动车组也不断增多。为了更加清晰地分析相同的速度级或者相同修程条件下动车组的安全规律，考虑我国动车组既有的修程设置（主要是相同检修周期的不同走行公里的规定）和速度等级（主要考虑200～250 km/h、300～350 km/h 这2 个速度级），将不同车型动车组划分为4 个分析类别，具体划分方法见表1。

文中以某分析类别动车组百万公里故障率数据为例，研究建立灰色GM（1，1）残差修正模型。该分析类别动车组百万公里故障率数据变化趋势如图1 所示。

图1 呈现出该分析类别动车组百万公里故障率数据具有如下特点：

（1）非线性；

（2）数据波动变化具有动态随机性。

灰色预测模型是预测理论中的一种重要方法，是一种研究少数据、贫信息不确定性问题的方法［8］。它的突出优点是可以有效地处理系统内部信息的不确定性因果关系，通过对时间序列的累加，弱化其随机性［9］。文中采用灰色系统理论，建立灰色GM（1，1）残差修正模型，对动车组百万公里故障率进行研究。

表1 动车组自定义分析类别划分说明

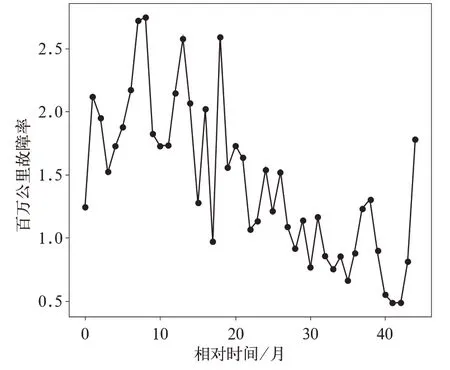
图1 某分析类别动车组百万公里故障率变化趋势图

2 GM(1,1)模型的建立[7-10]

由文献［7］可知，灰色GM（1，1）模型可分为等时距模型和非等时距模型。文中建立的模型为等时距模型，时间间隔为1 个月。

（1）设某分析类别动车组的百万公里故障率数据序列为X(0)={ x(0)(1)，x(0)(2)，…，x(0)(n)}，对原始序列构造一次累加生成（1-AGO）序列，得：X(1)={ x(1)(1)，x(1)(2)，…，x(1)(n)}，令 x(1)(1)=x(0)(1)；式中：

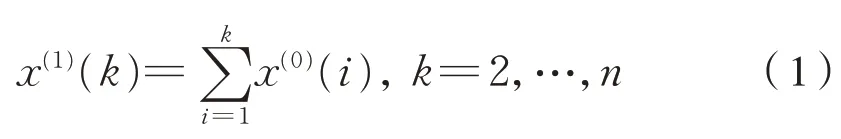
（2）由生成序列X（1）建立白化形式的微分方程为式（2）。

式中：a 为发展系数，用以控制灰色系统发展态势的大小；u 用以反映数据变化的不确切关系，又称为灰色作用量［7］。

对式（2）在区间[k-1，k]上积分，得到式（3）：

GM（1，1）模型的拟合精度与参数a^ =[a，u]T有关，而a^ =[a，u]T的取值又依赖于原始序列和背景 值 Z(1)=(z(1)(2)，z(1)(3)，…，z(1)(n)) 的 构 造 形式［7］，为了提高模型精度，减小误差，文献［7，10］提出了一种基于积分重构GM（1，1）模型背景值的方法，按照该方法，对Z(1)进行优化的计算方法为式（9）：

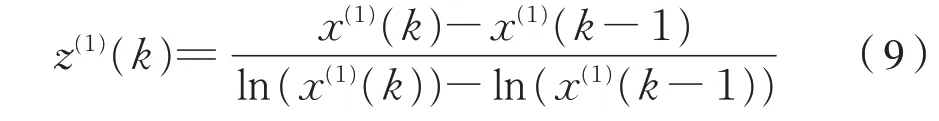
式中：k=2，…，n。文献［7，10］证明按照式（9）构造的背景值更接近实际。

3 残差修正

为进一步提高模型的拟合度，对残差序列进行修正，修正方法如下：

设残差数列为式（10）：

设 样 本 集D={(x1，q1)，(x2，q2)，…，(xn，qn)}，回归问题就是找到一个函数f(x)，使得f(xi)与真实值qi的误差能够尽可能小。以支持向量机SVM（Support Vector Machine）为理论基础建立的回归模型，在准确度、收敛速度和风险控制等方面都有很好的性能［11］。因此用支持向量回归机SVR（Support Vector Regression）对残差数列Q进行回归拟合。

对 于 训 练 集D={(x1，q1)，(x2，q2)，…，(xn，qn)}为非线性的情况，支持向量回归机的基本思想是通过一个非线性函数Φ，将数据x映射到高维特征空间F，并在这个特征空间进行回归［12］。

为了提高预测精度，在用支持向量回归机对残差进行回归拟合时，把t-k，t-（k-1），…，t-1 时刻的残差作为输入，t时刻的残差作为相应的输出。经参数调整，把t-3，t-2，t-1 时刻的残差作为输入，t时刻的残差作为输出时，拟合的精度较高。核函数选择高斯核函数时，对残差的拟合精度较高。

对 残 差 数 列Q={q(1)，q(2)，…，q(n)} 用 支 持向量回归机进行回归拟合，得到残差的拟合数据序列，见式（11）：

根据式（8）、式（10）和式（11），得到最终优化的灰色GM（1，1）修正模型为式（12）：

4 模型实例应用检验

采用某分析类别动车组在相对时间0～44 个月的百万公里故障率数据。用文中给出的优化背景值后的灰色GM（1，1）模型对该分析类别动车组在该时间段内的百万公里故障率数据进行拟合，原始百万公里故障率数据及其拟合结果对比如图2所示。

图2 表明该分析类别动车组百万公里故障率总体上呈现出下降的趋势。由真实值减去优化背景值后的灰色GM（1，1）模型拟合值得到的残差如图3 所示。

图3 显示出该分析类别动车组百万公里故障率数据的残差呈现非线性的正负交替的情况，这说明原始百万公里故障率数据中含有一定的随机成分。动车组故障形成是多种因素共同作用的结果，且动车组行车环境复杂，得到的残差具有随机波动性，符合实际意义。图3 呈现的残差变化波动趋势与图1 原始百万公里故障率数据的变化波动趋势相似，进一步说明优化背景值后的灰色GM（1，1）模型能够较好的呈现该分析类别的动车组在该时间段内的百万公里故障率的趋势成分。为了提高模型的拟合精度，用支持向量回归机对残差 进 行 修 正，将t-3，t-2，t-1 时 刻 的 残 差 作 为输入，t时刻的残差作为输出，核函数选用高斯核函数。经过超参数调整后，原始百万公里故障率数据与经过残差修正后的百万公里故障率拟合数据的对比如图4 所示。

图2 百万公里故障率及其拟合结果对比

图3 残差变化趋势图

用平均相对误差作为检验指标时，图4 中的灰色GM（1，1）残差修正模型得到的百万公里故障率拟合值与真实值的平均相对误差为0.076；用统计学中的后验差C和小概率P检验法［7，9］进行模型精度检验，得到后验差比值C=0.150，小误差频率P=1.00；由文献［9，15］可知，一般根据C、P的值将预测精度分为4 级，见表2。

对照上表可以看出文中给出的灰色GM（1，1）残差修正预测模型的精度属于好的范畴，可以用于外推预测。

用图4 得到的灰色GM（1，1）残差修正模型对相对时间45 个月的百万公里故障率数据进行预测，得到预测值为0.85，相对时间45 个月的百万公里故障率数据的真实值为0.81，相对误差为4.94%。

将相对时间45 个月的百万公里故障率数据加入模型，删除原始百万公里故障率数据中的第一个数据，进行模型更新，得到新的等维灰色GM（1，1）残差修正模型，用此模型对相对时间46 个月的百万公里故障率进行预测。依次类推，得到相对时间47～49 个月的故障率预测模型。相对时间46～49 个月的原始百万公里故障率数据与模型拟合值的对比如图5 所示。

图4 原始百万公里故障率与残差修正后的拟合结果对比

表2 精度检验等级参照表

图5 相对时间46～49 个月的原始百万公里故障率与残差修正后的拟合结果对比

相对时间46～49 个月的故障率预测模型的各项评价指标见表3。

由表3 可知，残差修正后的等维灰色GM（1，1）模型能较好地拟合百万公里故障率数据的变化趋势以及波动大小。

用等维灰色GM（1，1）残差修正模型对相对时间45～49 个月的百万公里故障率的预测值与真实值的对比见表4。

表3 各预测模型指标值

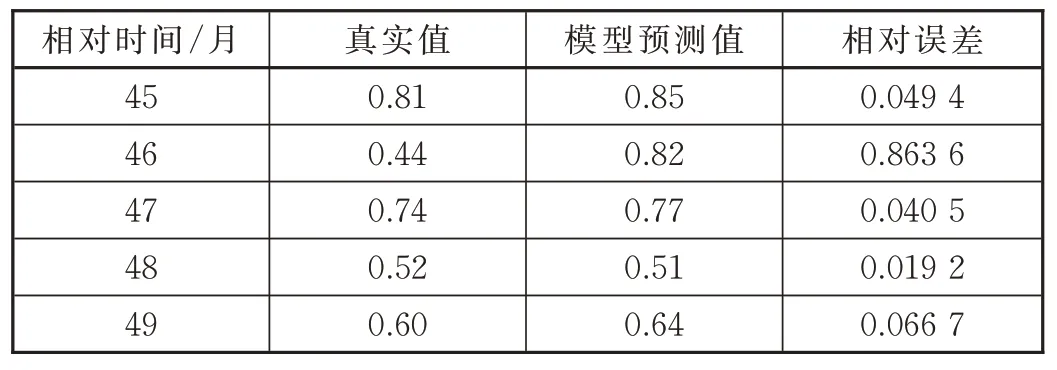
表4 模型预测值与真实值的比较

5 结 论

（1）根据灰色系统理论的时间序列处理原则，在等时距灰色GM（1，1）模型的基础上，通过优化背景值的方法，建立了预测动车组百万公里故障率变化趋势的模型，利用支持向量回归机对优化背景值后的灰色GM（1，1）模型的残差进行修正，拟合了某分析类别动车组百万公里故障率数据的波动大小，并通过等维信息灰色GM（1，1）模型来对建模数据进行更新。计算实例表明，等维灰色GM（1，1）残差修正模型能够较好的拟合动车组百万公里故障率的变化趋势与波动程度，且有较好的预测精度。

（2）由于用来建模的原始百万公里故障数据波动较大，给长期预测带来了挑战。计算实例表明，该模型能够较好地拟合历史数据，却无法预测出现较大波动的数据，如何进一步处理原始数据，减小原始数据波动性对模型性能的影响以及挖掘更多影响百万公里故障率的因素是下一步研究的内容。