铝蜂窝在准静态压入下的尺寸效应

焦萌学，邱 吉，金 涛，王志华

(太原理工大学 机械与运载工程学院，太原 030024)

铝蜂窝作为一种典型的多孔材料具有密度小、比强度高、比刚度高等优点，在工程中被广泛应用于承载或吸收冲击能量的结构中。有关铝蜂窝在准静态及动态的面内外压缩等力学行为，前人已经进行了十分详尽的研究和建模[1-4]。然而在工程运用中，铝蜂窝经常要承受多种类型的复杂载荷，研究在复杂载荷下多孔材料的力学响应是当前的一个热点。ASHAB et al[5]在准静态和动态压入实验中探究了应变率对铝蜂窝平台应力和能量吸收的影响，并提出了一个撕裂能关于应变率的经验公式。ZHOU et al[6]使用Arcan加载装置完成了组合的剪压应力状态，并提出了相应的破坏准则。此外他们还研究了平面定向角对组合载荷作用下蜂窝结构屈服行为的影响。

多孔材料的力学性能与其基体材料属性、胞孔的几何特征等多种因素有关。由于多孔材料结构的特殊性，其力学行为在特定尺寸范围内经常表现出与试样尺寸相关的尺寸效应。ANDREWS et al[7]通过单轴压缩、剪切、压痕等实验证明了泡沫铝试样的材料力学行为有强烈的尺寸依赖性。JIN et al[8]通过铝蜂窝的面外和面内单轴压缩实验，发现了随着面内尺寸的增加，面外方向的宏观刚度降低，而面内方向的宏观刚度增加。而且随着尺寸的持续增大，宏观刚度趋于稳定，由此得到测量蜂窝铝力学性能的最小尺寸为胞元数N=13×13.

有关以上两个研究方向已有大量的研究和文献发表，而将两者结合的在复杂载荷下铝蜂窝材料的尺寸效应研究却十分匮乏。铝蜂窝在防撞结构中作为芯层材料，经常要承受压入载荷。ZHOU et al[9]在其研究中定义了撕裂强度来描述铝蜂窝在压入实验中压头四周撕裂的情况。本文采用3种不同密度的蜂窝试件进行面外单轴压入实验，通过设计一种压入位置可控的压入实验得到单层胞壁和双层胞壁在压入实验中的撕裂力，分析了压入实验中铝蜂窝的变形模式，并最终得到压头尺寸对铝蜂窝压入实验中平台应力、撕裂强度力学参数的影响。

1 实验方案

1.1 实验材料

实验采用3种不同密度的商用六边形铝蜂窝。铝蜂窝的基体材料均为5052铝，以不同的相对密度分别命名为H12，H21，H41.其中对于铝蜂窝的相对密度ρr有：

式中：ρ*为铝蜂窝样品的密度，kg/m3；ρs为铝蜂窝基体材料的密度，kg/m3；t为蜂窝单层胞壁厚度，mm；D为六边形蜂窝胞元的边长，mm；θ为蜂窝胞元的拓展角。3种铝蜂窝详细的规格参数见表1.铝蜂窝常用的制造方法有拉伸法和成型法两种[10]，实验所用的铝蜂窝均采用拉伸法制成，每个蜂窝胞孔由4个单层胞壁和2个双层胞壁围成，其中双层胞壁通过两个单层胞壁胶合而成。实验所采用的3种六边形商用铝蜂窝及其结构示意图如图1所示。

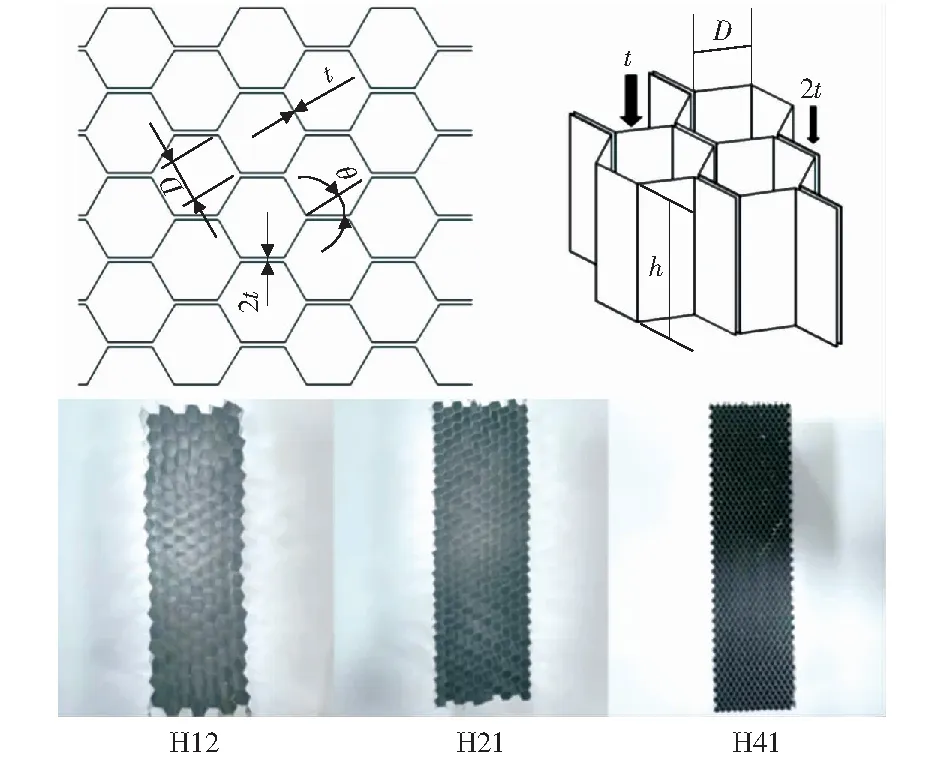
图1 实验所用铝蜂窝及其结构示意图Fig.1 Aluminum honeycomb specimens used in the experiment and their structure diagram

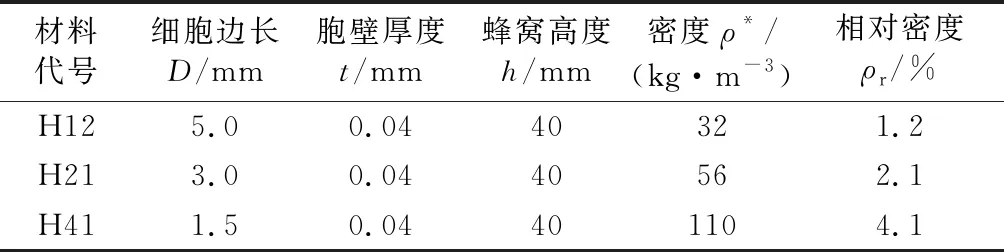
表1 铝蜂窝的规格Table 1 Specification of aluminum honeycomb specimens

1.2 压缩实验

本实验采用万测万能材料实验机(100 kN传感器)对3种密度的铝蜂窝试件进行准静态面外单轴压缩，设定恒定的加载速率为6 mm/min.在XU et al[11]的实验研究中提到，为了获得蜂窝结构稳定的力学参数，蜂窝试样面内尺寸(六边形胞元数目)至少应大于 9×9.因此，本文压缩实验所选试样胞元数均大于9×9.整个加载过程直至蜂窝完全密实化。加载装置及典型蜂窝材料的压缩应力-应变关系如图2所示。

图2 (a)加载装置及(b)蜂窝材料在压缩下的典型应力-应变关系图Fig.2 Loading device (a) and typical stress-strain relationship diagram of honeycomb material under compression(b)

1.3 压入实验

为了测量铝蜂窝在不同几何构型压头的准静态压入作用下的力学响应，实验采用了具有不同面积的正三角形、正方形、圆形3种不同形状的压头。其中不同的压头面积分别设置为400，900，1 600，2 500 mm2.部分实验所用压头如图3所示。为了简化描述对不同形状和尺寸的压头进行了如表2所列的命名。为了保证压入实验和压缩实验的可对比性，压入实验同样采用与压缩实验相同的加载速度。

图3 实验所用的部分压头Fig.3 Some indenters used in the experiment

ZHOU et al[9]的研究发现除了压头尺寸外，被压入的试样的几何尺度同样会影响压入的力学响应。为了确定压入试样的大小，加入一个简单实验探究在相同压头形状和面积下，不同试样尺寸(面外横截面面积)的压入情况。实验选用面积为2 500 mm2的方形压头，试样材料为H41，分别制作一个试样尺寸为压头尺寸5倍大小的试样和一个试样尺寸远大于压头尺寸(大于10倍)的试样。实验方法与普通压入相同。实验所得到的力位移图如图4所示。从图中可以看出随着试样尺寸的增大，实验所得的峰值力和平台力都会减小，尤其是峰值力。产生这种现象的原因是随着试样尺寸的增大，被压入的蜂窝周围的束缚增强，使蜂窝更容易进入撕裂和压缩复合的平台阶段。当试样面积小时，周围束缚不足，试样四周有翘起的趋势，整个试样产生了更多的变形区域，从而加大了进入平台阶段所需的力。

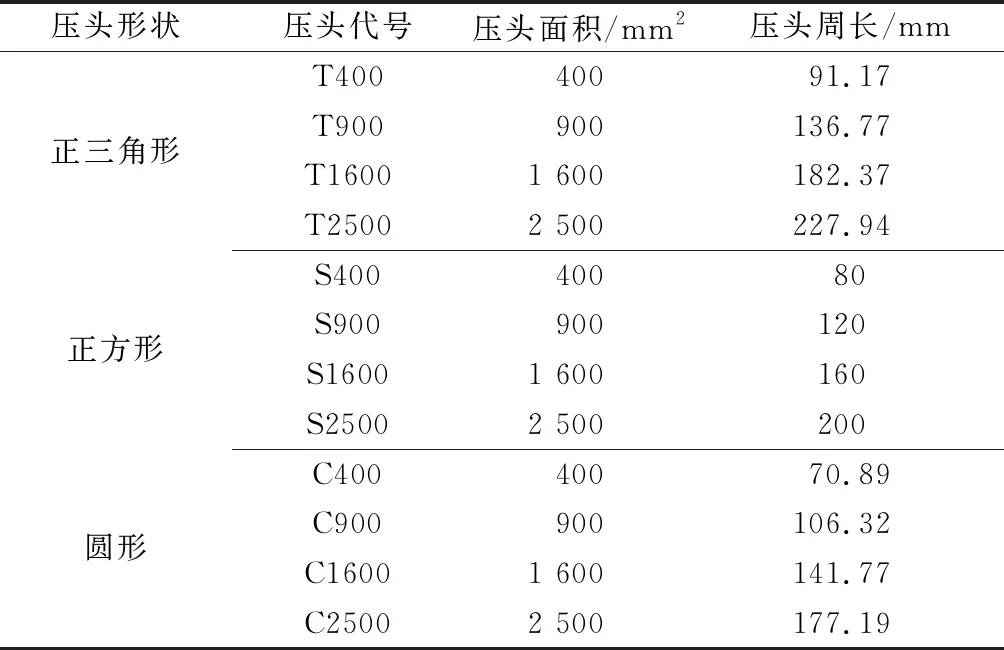
表2 压头的规格Table 2 Specification of indenters

图4 不同试样尺寸的压入力位移曲线与实验图Fig.4 Indentation force-displacement curves and experimental diagrams of different model sizes

1.4 单、双层胞壁压入实验

在普通压入实验中发现，蜂窝的撕裂集中在压头边缘，但压头在撕裂单层胞壁和双层胞壁时，产生了明显不同的变形模式(详见2.2).同时在实验过程中，因为压入区域被样品包围，无法观测到整体的变形模式，在此引入一个新的压入实验来观察和分析压入实验中蜂窝的变形模式，并比较在撕裂单层胞壁和双层胞壁时的力学特征。

新的压入实验采用与上述两个实验相同的万能实验机和铝蜂窝实验材料。六边形蜂窝的面外结构示意图如图5所示，对于正方形和三角形压头，其直线边缘在撕裂蜂窝胞壁时存在如图中所示的4种典型状况，其中D代表压入边与双层胞壁垂直的状态，S代表压入边与单层胞壁垂直的状态，SS代表压入边与D垂直且全部压在单层胞壁上，DS代表压入边与S垂直间隔压在双层和单层胞壁上。

图5 压入实验压入位置示意图Fig.5 Schematic diagram of the press-in position of press-in experiment

本实验采用正方形压头，通过切割样品、控制压头大小和压入位置可以保证正方形压头对称两边处于相同的撕裂位置，另外两边不参与撕裂，这样就可以测量每种典型状况的撕裂力学性能。之前提到试样尺寸对压入实验结果的影响，在普通压入实验条件下，选用了足够大的样品以消除这样的影响。由于本实验中压头下方区域相比普通压入缺少两个方向上的约束，采用长度大于压头边长3倍的实验样品，并在样品两端加入固定约束，来模拟足够大的样品在压入实验中的状态。本实验方法示意图如图6所示。与普通压入实验相同，加入一组试样两端为自由约束的实验进行对比。实验及结果对比如图7所示。从实验现象及结果可以看出，与普通压入实验类似，拥有固定约束的实验组平台力与峰值力都小于自由约束实验组，在压入过程中由于缺少了两个方向的约束，自由约束实验组试样两端有了更明显的翘起。与普通压入实验对比可见，选择两端加

图6 压入实验设计示意图Fig.6 Schematic diagram of press-in experiment design

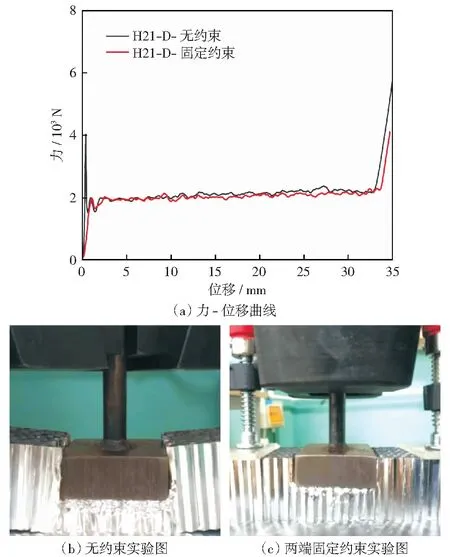
图7 不同约束下D类压入实验及结果对比Fig.7 Type D indentation experiment and comparison of results under different constraints

入固定约束来模拟足够大的样品是可靠的。

2 实验结果与讨论

2.1 实验结果的重复性

在本文中，为了保证实验结果的可靠性，所有的测试都重复了3次。图8显示了蜂窝试样压缩和压入实验结果的重复性。对于H41蜂窝压缩实验，H41-1，H41-2，H41-3试样的平均平台应力分别为2.16，2.12，2.08 MPa.最大差异约为3.77%.对于H12在S900压头下的压入实验，H12-S900-1，H12-S900-2，H12-S900-3平均平台力分别为318.51，319.97，336.44 N.最大差异约为5.62%.对于H21在T1600压头下的压入实验，H21-T1600-1，H21-T1600-2，H21-T1600-3平均平台力分别为1 562.760，1 600.040，1 599.484 N.最大差异约为2.39%.对于H41在C1600压头下的压入实验，H41-C1600-1，H41-C1600-2，H41-C1600-3平均平台力分别为2 271.72，2 290.52，2 274.52 N.最大差异不足1%.可以看出，在相同加载条件下，3条曲线非常接近。因此，实验产生的误差可以忽略不计，即本文实验数据是可靠的。

2.2 变形模式

对于蜂窝压入实验，图9所示为典型的压入实验曲线和相同尺寸的压缩曲线。从图中可以发现，面外单轴压入曲线与面外单轴压缩类似，可以分为典型的3个阶段：初始弹性阶段、平台阶段、密实化阶段。两者的主要差别在于初始弹性阶段的峰值力与平台阶段的平台力。

图8 铝蜂窝在各类实验中的重复性Fig.8 Reproducibility of aluminum honeycomb in various experiments

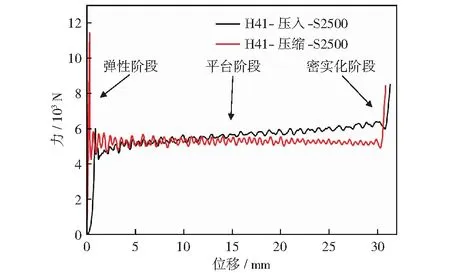
图9 相同尺寸的H41压入和压缩实验的力-位移曲线Fig.9 Force-displacement curve of H41 indentation and compression experiments of the same size

对于准静态压缩实验，在初始弹性阶段首先整体单元壁发生弹性变形，应力快速上升以达到足够使整体发生屈曲的水平，即峰值应力。在经历屈曲变形后，细胞壁最终进入周期性的塑性折叠阶段，即第二阶段平台阶段。对于样品足够大的准静态压入实验，变形区域周围有很强的约束与支撑，使得初始变形只限制在压头下方很小的区域范围内，不需要整体发生屈曲变形，就可以进入压头边缘撕裂，同时伴随着蜂窝周期性折叠的复合平台阶段。此时的细胞壁折叠从压头下部开始发生。因此准静态压入实验中峰值力明显小于准静态压缩实验。

同时，在图中可以明显发现，准静态压缩实验中，平台阶段是基本处于平稳状态，而准静态压入实验中，平台力却有缓慢上升的趋势。在XU et al[2]的研究中提到了蜂窝孔中的空气对蜂窝的增强效应。他们发现，在平面外动态压缩实验中，尤其在较高应变速率和孔百分比下，由于蜂窝孔夹带的空气无法及时溢出，空气压力导致了蜂窝强度增加。然而本实验采用了较低的准静态范围内的应变率，显然空气压力不是造成平台力上升的主要因素。

ZHOU et al[9]将铝蜂窝压入实验中超过弹性区域的4种主要变形机制分类为剪切、撕裂开始、撕裂传播和压缩。在本实验中，同样观察到类似的现象。如图10所示是H41在两种压入实验压入后的实验样品的典型情况。图10(a)和10(b)所示为D类撕裂情况，即压头边缘与双层胞壁垂直。图10(c)和图10(d)为SS类撕裂情况，即压头边缘间隔压在单层胞壁和双层胞壁上。从图10中可看出通过普通压入实验得到的样品与本文设计的区别单双层胞壁的压入得到的实验样品在相同的一侧有类似的变形模式。这证明了本文设计的实验对于分别测量单双层胞壁撕裂情况是可行的。对于D类撕裂，撕裂开始后，裂纹有向周围扩展的趋势，并且随着压入深度的增大，裂纹扩展越明显，甚至侵入了周围的胞元。在蜂窝完全密实化后，压坑会略大于压头面积。而对于SS类撕裂，与D类撕裂形成明显对比的是撕裂十分整齐，从撕裂开始到完全密实化，并没有出现裂纹的扩展和压坑尺寸增大的现象。

图10 H41在两种压入实验压入后的实验样品的典型情况Fig.10 Typical situation of the test sample H41 after two press-in experiments

对于图10中H41单一情况的压入实验结果如图11(c)所示，从图中可以看出，D类撕裂状态下，撕裂力明显大于SS类撕裂，同时SS类撕裂中，平台阶段的斜率明显下降并趋近于平稳。结合图11(a)和图11(b)可以发现，在H12和H21蜂窝中，同样含有双层胞壁的压入方式其撕裂力大于只含单层胞壁的撕裂方式。因为H12和H21在相同压入面积下所包含的胞元数明显少于H41蜂窝，不同压入方式的撕裂力之间差别相对较小。在H41实验结果中发现，明显出现撕裂力D>DS>S>SS的现象。D类撕裂情况中，直接撕裂双层胞壁，同时与之相连的是较弱的两个单层胞壁。SS类撕裂中，直接撕裂单层胞壁同时与之相连的是较强的双层胞壁。结合实验现象分析，当蜂窝撕裂时，撕裂的胞壁本身强度越高，所需的撕裂力越大。同时与被撕裂胞壁相连的胞壁越弱，越容易出现裂纹扩展的现象，裂纹的扩展会进一步加大撕裂所需的力。根据以上实验现象与结果推测，在准静态压入实验中，引起平台力上升的主要原因是双层胞壁撕裂时产生的裂纹扩展。

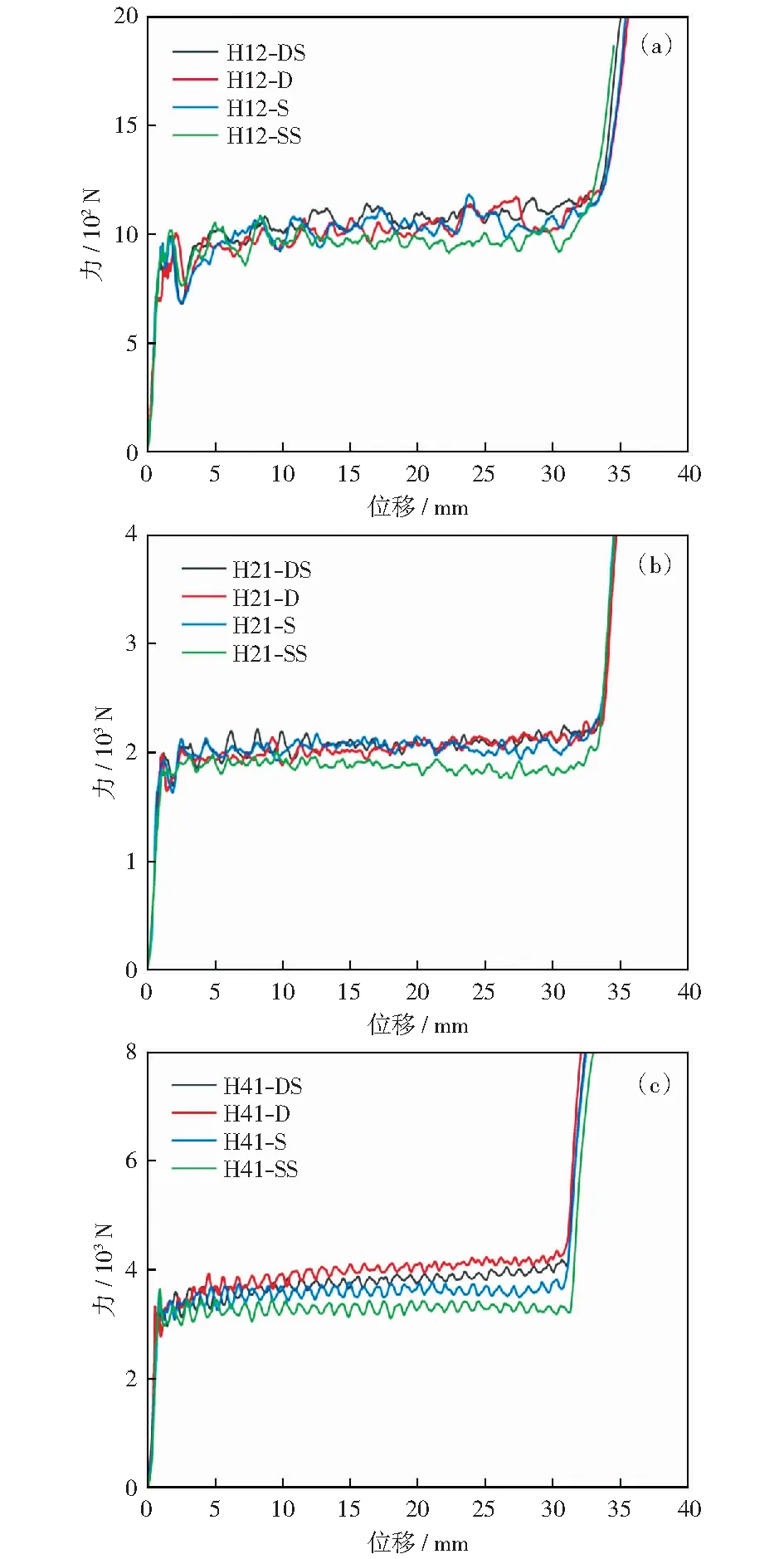
图11 不同压入方式的实验结果Fig.11 Experimental results of different indentation methods

2.3 撕裂强度的尺寸效应

蜂窝压入是一种涉及多种失效模式的响应行为，为了衡量压入实验中的力学参数，通常将蜂窝压入实验简化为压缩与撕裂的复合：

Ft=FT-Fc.

(1)

式中：FT是总压入力，Fc是压缩力，Ft是撕裂力。

蜂窝压缩的力学参数可以简单地通过压缩实验获得，在JIN et al[8]的研究中，压缩过程中的平台应力不具有尺寸效应，所以压入实验中的压缩力可计算为：

Fc=σcAc.

(2)

式中：σc是材料的平均平台强度，Ac是压入截面面积。

由于无法通过直接测量得到蜂窝压入的撕裂力，因此在式(1)计算过程中，保持压缩力Fc的准确性显得至关重要。如图12所示，蜂窝结构作为一种周期性结构，其最小的周期结构单元是Y型单元。本文采用Y型结构单元来衡量蜂窝在压缩实验中的受力面积。此时在计算蜂窝压缩的应力σ时有公式：

(3)

式中：F为压缩实验测得的压缩力，NY为试样所包含的Y型单元数，SY为单个Y型单元所占的面积。

图12 Y型结构单元示意图Fig.12 Schematic diagram of Y-type structure unit

对于平台应力，很多研究者[8，11-12]采用能效法计算密实化应变和平台应力。但在之前的研究中发现试样尺寸大小对峰值力有很大影响，因此，在本研究中，采用ASHAB et al[5]的计算方法，将压缩与压入实验的平均平台应力计算为位移5 mm～30 mm(应变0.125～0.750)的平均应力。

在压缩实验中，3种不同密度蜂窝结构的平均平台应力分别为0.323，0.695，2.108 MPa.压缩与压入实验的平均平台应力如图13所示。

图13 压缩与压入实验的平均平台应力Fig.13 Average platform stress of compression and indentation experiments

从图13中可以看出，对于压入实验，不同密度的蜂窝结构在不同形状和尺寸的压头下，均表现出平均平台应力随着压入面积的增大而减小，并有趋近于压缩平均平台应力的趋势。因此平均平台应力不能作为一个具有统计意义的衡量压入实验平均强度的力学参数。其中，同样的面积下，平均平台应力一般为三角形压头大于正方形压头大于圆形压头。由实验观察到，蜂窝的撕裂主要集中在压头边缘，而同样的面积下，压头的周长也是三角形压头大于正方形压头大于圆形压头，认为撕裂力应该是与压头周长相关。ZHOU et al[9]基于能量平衡方程提出了一种撕裂强度概念，其计算公式为：

Ft=ftlt.

(4)

式中：ft定义为蜂窝被压入时的撕裂强度，lt为撕裂长度(即压头横截面周长)。

用撕裂强度来衡量蜂窝压入实验中的撕裂强度在现今是被广为接受的。通过式(1)-式(4)可以得到3种不同密度蜂窝在不同压头尺寸下的平均撕裂强度ft，其结果如图14所示。

图14 蜂窝在不同压头尺寸下的撕裂强度Fig.14 Tear strength of honeycomb under different indenter sizes

由图14所示，对于密度最小的H12蜂窝，不同压头形状和不同压头尺寸下的撕裂强度呈现出稳定的波动状态。正方形、圆形、三角形压头的平均撕裂强度分别为2.34±0.17，2.33±0.19，2.09±0.14 kN/m.对于H21蜂窝，正方形和圆形压头的撕裂强度随着压头尺寸的增大具有缓慢上升的趋势，三角形压头依然呈现出波动趋势。正方形、圆形、三角形压头的平均撕裂强度分别为3.13±0.3，2.51±0.28，2.59±0.32 kN/m.对于H41蜂窝，正方形和圆形压头的撕裂强度随着压头尺寸的增大具有很快下降的趋势，三角形同样呈现出波动趋势。正方形、圆形、三角形压头的平均撕裂强度分别为3.48±1.14，3.24±1.24，3.72±0.7 kN/m.从整体分析来看，圆形和正方形压头在不同的密度下具有相同的变化趋势，而三角形压头的变化趋势比较混乱。在单双层胞壁压入实验中，设计了单层胞壁和双层胞壁的压入结果。实验证明，不同的撕裂情况之间的实验结果相差很大，也就是说压头撕裂的单双层胞壁的数量和比例，会影响压入的实验结果。理论上三角形比正方形和圆形更容易出现单双胞壁数量和比例的极端情况，其自身的实验误差也就越大。推测这就是引起三角形压头变化趋势混乱的主要原因。

对于圆形和正方形压头来说，在H12和H21蜂窝样品的实验中，尽管变化趋势不同，但实验所测得的撕裂强度误差很小，考虑到不同压入情况可能带来的自身实验误差，笔者认为在实验尺度中，平均撕裂强度可以作为衡量压入的撕裂的统计性参数。然而对于H41蜂窝样品，圆形和正方形压头产生了明显的撕裂强度随压头尺寸增大而减小的趋势，不同尺度之间的误差也很大，此时撕裂强度无法准确衡量压入的撕裂情况。

由于压缩力与面积成正比，而在本实验中认为撕裂与压头周长成正比，可以预见的是在压入实验中，随着压头尺寸的增大，撕裂力所占总力的比重会越来越小。当压缩力远大于撕裂力时，蜂窝的撕裂对于压入实验结果的影响会减弱。随着蜂窝密度的增大，相同面积下蜂窝的压缩强度明显提高，但单位长度内的胞元数并没有显著增长，撕裂力所占比重随着蜂窝密度的增大而显著减小，所以在H41蜂窝样品的实验中，撕裂对于压入成为了“弱影响”因素，此时撕裂强度失去稳定性，出现了明显的下降。因为撕裂强度通过计算总压入力与压缩力的差值得到，当撕裂力占比很小时，压缩力上微小的波动有可能造成撕裂强度产生巨大的误差。图15所示为不同密度的压入实验中撕裂力与总压入力的比例。对应实验所得的撕裂强度可提出经验性结论：当计算撕裂力占比小于总压入力的20%时，撕裂强度会失去稳定性，所测得的撕裂强度不能代表材料的强度参数。

3 结论

在本实验研究中，使用万能实验机在6 mm/min的恒定速度下对不同密度的铝蜂窝进行面外压入和压缩实验。通过改变压头的形状大小和压入的位置，测得压入实验中单层和双层胞壁的撕裂情况。对实验中由计算机记录的力-位移数据进行分析计算，得到了压缩和压入实验中的峰值力、平台应力、撕裂强度等参数。结合实验现象发现，在压入实验中，试样尺寸对压入的峰值力有明显影响，试样尺寸的增大使得压入区域周围有了更强的支撑，使峰值力显著降低。同时发现双层胞壁的撕裂力明显大于单层胞壁，被撕裂的胞壁本身强度越强，与之相连的胞壁强度越弱，所需要的撕裂力越大。双层胞壁撕裂时的裂纹扩展是引起压入实验中平台应力上升的主要原因。在保证试样尺寸足够大的条件下，通过改变压头的形状和大小发现，压入实验中3种不同密度的铝蜂窝的平台应力都随着压头尺寸的增大而减小并趋近于压缩实验的平台应力。H12和H21在实验范围内的撕裂强度基本保持稳定，而H41则表现出撕裂强度随压头尺寸的增大而减小的趋势。这是因为一般认为压缩的平台应力与面积成正比例关系而撕裂力与压头的周长(即撕裂长度)成正比例，随着蜂窝密度的增大，铝蜂窝压缩的平台应力显著增大，但单位长度上的胞元数并没有明显增长。撕裂力在总压入力中所占比例越来越小，逐渐成为弱影响因素，此时撕裂强度出现了不稳定现象，不能再作为衡量蜂窝撕裂情况的稳定力学参数。可以预见，对于H12和H21，随着压头尺寸的持续增大，撕裂强度也会出现相同的趋势。 在本实验中，当撕裂力占比小于总压入力的20%时，撕裂强度失去稳定性，因此建议在测量撕裂强度时，应保证撕裂力占比大于总压入力的20%.

图15 撕裂力与总压入力的比例Fig.15 Ratio of tearing force to total pressing force