基于地震均匀损伤的钢筋混凝土框架结构新型侧向力模式

白久林，刘明辉，孙博豪，陈辉明

(重庆大学 山地城镇建设与新技术教育部重点实验室；土木工程学院，重庆 400045)

传统结构抗震设计是根据作用在其上的侧向力进行内力分析和能力设计来获得结构沿高度的强度和刚度分布，因此，结构在强震下的抗震响应与结构的设计侧向力模式密切相关。目前，各国规范均建议了结构抗震设计时的侧向力模式。以规范体系为代表的侧向力模式，主要基于结构弹性振动状态时的楼层惯性力分布获得，其表达式相对简便，在实际设计时工程师便于应用，能很好地满足结构在小震弹性状态下的抗震性能要求。然而，当结构在大震下进入非线性状态后，基于弹性状态的设计侧向力不能确保结构在强震下的非线性抗震响应，常出现非预期的破坏模式[1-2]。

基于此，为确保结构在大震下的抗震性能，诸多学者发展了新型侧向力模式。Moghaddam等[3]基于层剪切模型，在对结构动力特性进行均匀损伤优化设计的基础上，提出了能考虑结构周期和设计目标延性的新侧向力模式。Chao等[4]根据实体钢框架结构在多条地震下的最大层间剪力分布，发展了基于结构非线性状态的新侧向力模式。为使结构获得各楼层变形相同的均匀损伤模式，Park[5]根据层模型结构的层间剪力需求，分别发展了适用于远场地震和近场地震作用的新侧向力模式。Hajirasouliha等[2]基于均匀损伤思想，对剪切结构模型进行优化设计，研究了基本周期、目标延性要求、层数、阻尼比、材料屈服后性能和地震动激励对优化侧向力分布模式的影响，并提出了一种参数范围更广泛的新型侧向力模式。此外，为考虑土-结构动力相互作用效应(SSI)，Ganjavi等[6]提出了弹性层剪切结构的新型侧向力模式。Lu等[7]对考虑SSI的多层剪切模型的抗震性能进行了综合参数研究，研究了不同侧向力模式对结构抗震参数的影响。孙国华等[8]和李慎等[9]分别对钢框架-钢板剪力墙结构和高强钢组合K形偏心支撑钢框架在近场和远场地震下的层剪力分布进行了研究，发现按照规范模式的拟合形式具有更高的精度。Li等[10]、Ganjavi等[11]也对侧向力模式进行了相关研究。

当前对新型侧向力模式的研究，主要基于双线性层剪切模型或钢框架结构在大震均匀损伤状态时的楼层剪力分布获得，并不能完全反映结构的非线性特性，特别是混凝土结构。对于RC框架结构，系统地考虑结构体系形成均匀损伤状态、土-结构动力相互作用、非线性滞回模型等多因素的新型侧向力还未见报道。基于此，笔者构建了RC框架结构均匀损伤优化设计，发展了基于中国规范格式的新型侧向力模式，可为结构抗震设计提供依据。

1 地震均匀损伤优化设计

优化准则法是土木工程结构诸多优化设计方法中的一种，其预先规定一组优化设计所必须满足的准则，然后根据这些准则建立达到优化设计的迭代公式，求出满足全部约束条件并使目标函数取最小值的设计变量近似解[12]。优化准则法简便、易于操作，不需要计算梯度，且优化过程与优化变量的数目无关，一般通过数十次迭代便能达到收敛条件[13]。考虑到地震均匀损伤优化设计需要计算结构的非线性响应，计算量大，且优化的变量较多，笔者采用优化准则法来进行设计。

优化设计基于两个假设：1)构件具有足够的箍筋可确保不发生剪切破坏；2)梁柱节点为刚性连接，节点不会发生破坏。这两个假设便是结构抗震设计时“强剪弱弯、强节点弱构件”的设计准则。

1.1 目标函数

优化设计基于均匀损伤的思想[14-17]，将结构损伤分布的均匀程度作为优化目标函数。层间位移角作为衡量结构抗震性能最重要的参数之一，其竖向分布的均匀性是均匀损伤抗震设计的核心。因此，目标函数可采用

(1)

式中：covIDR0和covIDR分别为优化前后结构最大层间位移角分布的变异系数。随着优化的进行，目标函数越来越小，层间位移角分布逐渐趋于均匀，最终实现均匀损伤设计的目标。

1.2 优化变量

对于RC框架结构，在结构高度和跨度一定的情况下，影响结构抗震性能的主要参数是梁柱的截面尺寸和截面配筋。由于RC构件截面尺寸与小震下结构的弹性刚度有关，一般要提前确定。因此，仅选取截面配筋作为优化变量，梁柱的截面尺寸则保持不变。对于框架柱，由于截面采用对称配筋，柱截面配筋仅有一个设计变量。对于框架梁，设计变量为梁上部钢筋和梁下部钢筋两部分。

1.3 约束条件

1)梁柱构件需满足最大和最小配筋率要求。最小配筋率和最大配筋率可根据规范要求获得。

ρcmin≤ρc≤ρcmax

ρbtmin≤ρbtop≤ρbtmax

ρbbmin≤ρbbot≤ρbbmax

(2)

式中：ρc、ρcmin和ρcmax分别为柱端截面配筋率、最小和最大配筋率；ρbtop、ρbtmin和ρbtmax分别为梁端上部截面配筋率、最小和最大配筋率；ρbbot、ρbbmin和ρbbmax分别为梁端下部截面配筋率、最小和最大配筋率。需注意的是，优化设计针对平面框架结构开展，优化时仅能优化柱单边的配筋。中国抗震规范规定了框架柱的最大配筋率[18]，要求柱的最大配筋率不超过5%。考虑到柱角筋有一定重复，取单边最大配筋率为1.5%。同时，规范中框架梁端截面底部和顶部纵向受力钢筋截面面积的比值也在优化中考虑(即一级抗震等级不小于0.5，二级抗震等级不小于0.3)。

2)梁构件需满足正常使用极限状态的要求，在竖向荷载下需保持弹性状态。当某些梁在竖向荷载下屈服时，可根据钢筋应变按式(3)进行迭代，使其满足弹性状态。

(3)

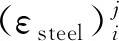
3)结构优化前后，材料成本保持不变。由于优化变量为梁柱钢筋，因此，在优化过程中，梁柱的总钢筋用量保持不变。

1.4 收敛条件

收敛条件为：连续两步目标函数之差的绝对值小于误差限制时则判定为收敛，如式(4)所示。在优化的过程中，可能会出现不收敛的情况。此时规定超过30步仍未达到收敛时则在30步时停止。

|fi-1-fi|≤e0

|fi+1-fi|≤e0

(4)

式中：fi为第i次迭代的目标函数；e0为误差限值，取值为0.01。

1.5 优化设计

地震均匀损伤优化设计基于优化准则法来开展，主要包括“分析→重新设计”的基本过程，具体优化步骤如下：

1)确定初始的结构配置参数，并建立结构的非线性有限元模型。

2)选择合理的地震输入，并对结构进行大震作用下的非线性分析。地震动的选取可根据“所选多条地震动的反应谱与规范设计谱在周期附近最大程度的拟合”原则来选取，地震动条数一般不少于10条。记录每条地震动下结构的最大层间位移角(IDR)分布和梁柱转角(θ)分布，并对其进行统计分析，获得整个结构的层间位移角平均值IDRave、结构柱端转角平均值(θc)ave和梁端转角平均值(θb)ave。

3)根据收敛准则进行判断。若收敛，则停止优化，此时的结构为最优设计，实现了均匀损伤的目标。否则按步骤4)继续运行优化程序。

4)对结构进行重新设计。当收敛准则不满足要求时，结构的层间位移角一般是不均匀分布的。根据“均匀损伤”的基本定义，梁柱截面钢筋将从层间位移角较小的楼层转移到层间位移角较大的楼层。此外，结构的层间变形还与梁柱构件的局部变形有直接关系。因此，在构建优化设计时，同时考虑结构的宏观(层间位移角)和微观(梁柱转角)损伤指标。梁柱截面新的配筋可根据式(5)～式(7)获得。

(5)

(6)

(7)

根据式(5)～式(7)可以发现，当梁柱构件所在楼层的层间位移角比其平均值大、梁柱构件的转角也比转角平均值大时，梁柱构件的配筋将会得到加强，此时梁柱构件的地震损伤有望降低。反之，当层间位移角和梁柱转角较小时，梁柱钢筋将会减少，梁柱构件地震损伤将会变大。通过对“损伤大的构件加强、损伤小的构件削弱”的优化设计，结构的地震损伤实现均匀分布。

5)在得到新的梁柱截面配筋之后，按式(2)～式(4)进行材料成本、配筋率等约束条件限制，获得优化后的结构模型。

整个优化流程如图1所示。

图1 优化设计流程图Fig.1 Optimization the flow chart

2 结构分析模型

为检验所提出均匀损伤优化设计方法的有效性，分别选取5层和8层的考虑了土-结构相互作用(SSI)影响的RC框架结构进行分析和验证。

2.1 结构基本参数

两个RC框架结构的立面图和梁柱构件的截面尺寸如图2所示。初始结构设计根据中国抗震设计规范进行[18]。5层结构为3跨，跨度为5 m；8层结构为4跨，跨度为6 m。两个结构均采用C30混凝土、HRB400钢筋，且都位于场地类别为Ⅱ类、设计地震分组为第一组的场地上。5层结构抗震设防烈度为8度(0.2g)，8层结构抗震设防烈度为8度(0.3g)。

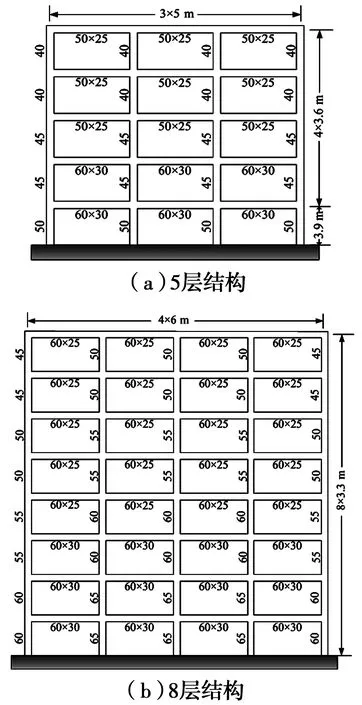
图2 RC框架结构立面和梁柱尺寸(cm)Fig.2 Structural elevation and beam and column configurations of RC frames (cm)

2.2 结构分析模型

采用OpenSees软件来建立结构的有限元分析模型[19]。上部梁柱构件采用基于力的集中塑性铰单元(beam with hinges)，其中，塑性铰长度取截面高度。为考虑混凝土开裂等对构件刚度的影响，对单元中间弹性部分的刚度进行一定的折减。截面采用可考虑轴力-弯矩耦合效应的纤维截面模型。混凝土采用Concrete 01模型；钢筋采用Steel 02模型。下部浅基础采用非线性Winkler地基梁模型(BNWF)来模拟土-结构相互作用的影响[20]，如图3所示。BNWF模型由竖向的多个q-z弹簧(模拟基础的沉降、摇摆和隆起)和水平的p-x弹簧(模拟被动土压力)和t-x弹簧(模拟基础与地基之间的摩擦力)组成，目前其已成为土-浅基础-结构相互作用体系地震分析的首选模型。

在OpenSees模型中，q-z、p-x和t-x弹簧均采用零长度单元来连接刚性地基与表征基础的弹性梁柱单元(Elastic Beam Column Element)。土体性能通过具有不同滞回性能的弹簧来模拟，其中q-z弹簧采用QzSimple2材料来模拟，其具有不对称的滞回响应，即受压强度高、拉伸强度较低。在基础端部水平布置的p-x和t-x弹簧分别选用PxSimple1材料和TxSimple1材料来模拟。PxSimple1材料具有捏缩的滞回曲线，能考虑卸载时基础与地基之间的间隙和被动土压力的影响。TxSimple1材料具有饱满的滞回性能，可较好地模拟与基础滑动相关的摩擦行为。BNWF模型的参数可根据基础数据和地基土参数计算确定。

图3 BNWF模型示意图Fig.3 BNWF model schematic diagram

2.3 地震输入模型

从PEER强震地震数据库中选取了10条天然地震动[21]，地震动的详细信息可参考文献[22]。10条地震动的选取是基于PEER的调幅方法，即将所选地震动反应谱的中位值与中国抗震设计规范反应谱最大程度的吻合。结构分析时，阻尼采用Rayleigh阻尼(阻尼比为5%)，考虑结构的重力P-Δ效应。将10条地震动调幅到大震水平，即对5层和12层结构，将地震动的加速度峰值调整到400 cm/s2，8层结构调幅到510 cm/s2。然后，对3个结构进行非线性动力分析，根据抗震响应参数进行结构的优化迭代。

3 优化设计结果

在建立的优化设计程序中，收敛参数α和γ的取值将直接影响优化速度和收敛效果，因此，需对收敛参数进行敏感性分析。图4给出了不同收敛参数对8层优化结构的影响。从图4可知，随着优化的不断进行，目标函数有减小的趋势，且随着收敛参数数值的增加，收敛速度加快，所需要的迭代步数较少。当α=γ=1.0时，结构均不能收敛。此外还可发现，当收敛时，无论收敛参数的取值为多少，目标函数的最终收敛值是大致相同的。这表明结构的最终优化结果和损伤分布的均匀程度大致相同，与收敛参数的取值关系不大。综合考虑收敛的稳定性、收敛速度，建议在地震均匀损伤优化时，收敛参数α和γ取值均为0.2。

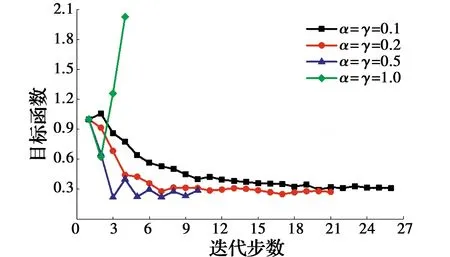
图4 收敛参数对8层结构优化结果的影响Fig.4 Influence of different converging parameter on the final solution of 8-story frame

图5给出了8层结构在优化过程中梁柱钢筋的变化情况。由图5可以看出，随着优化的进行，各层梁柱钢筋均发生了变化。对于梁构件，在整个优化过程中，2～5层梁的配筋先逐渐增加后保持不变；6层梁配筋总体上未发生变化；4层配筋先减小后又轻微地增加；1、7、8层梁的配筋先逐渐降低，后保持近似不变。对于柱构件，1层柱配筋一直稳步增加，5层柱配筋也略微有些增加；2～7层柱钢筋有略微降低，而8层钢筋降低较多。5层结构也有类似的分析结论。需指出的是，正是由于结构梁柱构件配筋的相互转移，才使得结构的损伤逐渐趋于均匀。

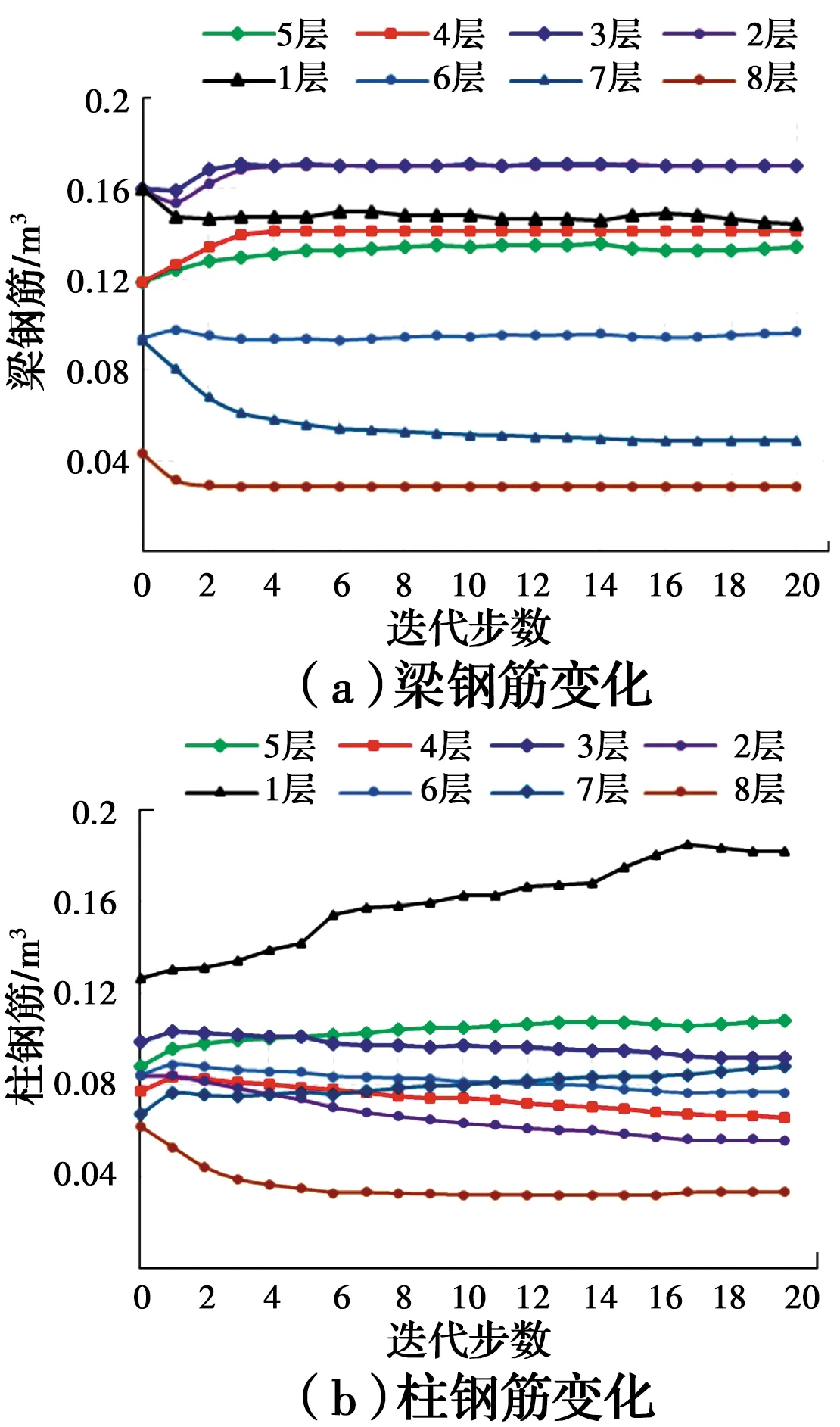
图5 8层RC框架优化过程中各楼层钢筋变化情况Fig.5 Variation of story reinforcements of 8-story RC frame in the optimization process

需注意的是，梁柱转角作为构件的局部损伤指标，被用来建立均匀损伤优化设计程序。为量化分析优化前后结构的梁柱转角大小，以5层结构为例，图6给出了等造价优化结构与原始结构的梁柱转角中位值的对比。从图6(a)中可以看出，优化设计使得梁端转角分布更加均匀，同时，降低了梁端转角的最大值。对于柱端转角(图6(b))，在优化前后的转角值均较小，表明结构柱主要处于弹性状态，确保了结构的“强柱弱梁”破坏机制；同时，通过优化设计，结构柱在强震作用下将获得更小的柱端转角。

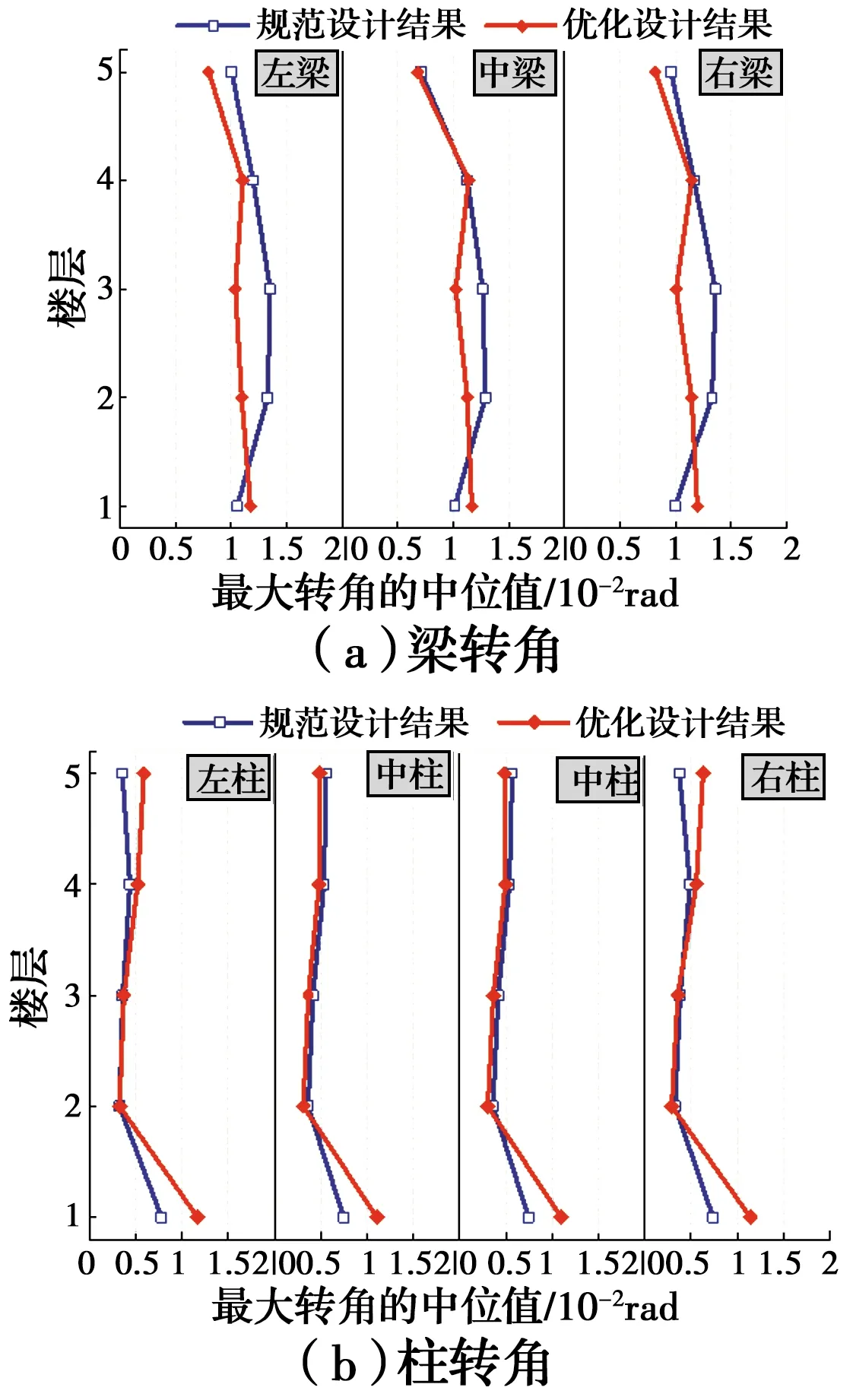
图6 5层结构梁柱最大转角中位值分布及对比Fig.6 Comparison of median beam and column maximum rotation for 5-story frame

为验证优化前后结构的均匀损伤分布情况，图7给出了结构在多条地震动下层间位移角分布及其平均值的分布情况。由图7可以看出，原始结构的层间位移角呈现出不均匀分布的情况，表明结构各楼层的材料并未得到充分利用。经过均匀损伤优化设计后，各楼层的材料得到了充分利用，结构的层间位移角均趋向于均匀化。此外，优化设计降低了结构的最大层间位移角，提高了结构的抗震性能。

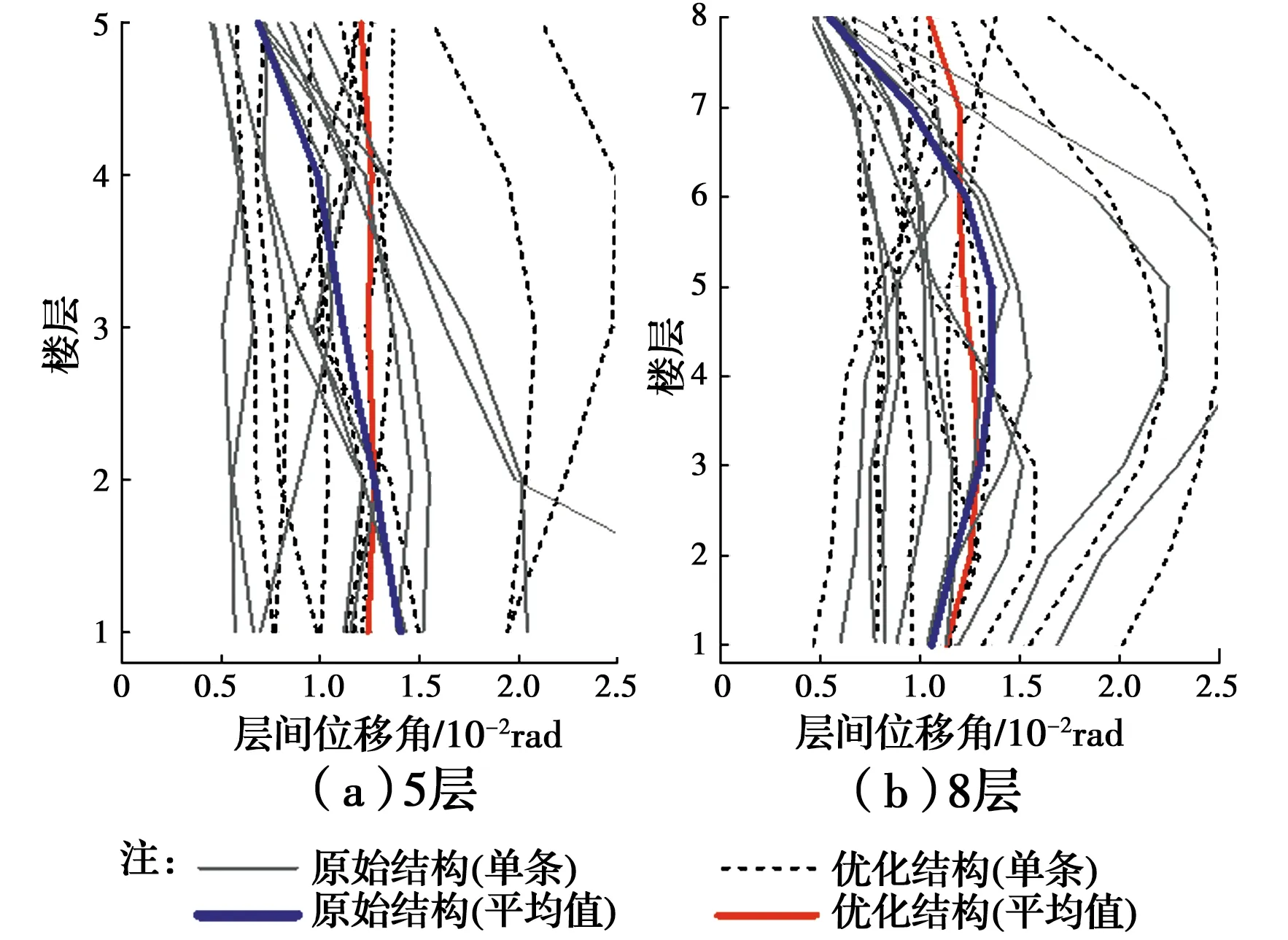
图7 优化前后结构的最大层间位移角对比Fig.7 Comparison of maximum interstory drift ratio for original and optimized structures

4 新型侧向力模式

优化设计后的结构能实现均匀损伤分布，根据结构在均匀损伤状态时的楼层剪力分布，可获得新型的侧向力模式并用于结构抗震设计。对于3个优化设计结构，其层剪力分布系数βi(βi=Vi/Vn)如图8所示。需说明的是，讨论的层剪力分布系数是多条地震输入分析获得的结果。由图8可以看出，地震动对层剪力分布系数的结果有较大影响，不同地震动下得到的层剪力分布系数差异较大。为减小地震动对层剪力分布系数结果的影响，最终的层剪力分布系数取10条天然地震动计算结果的平均值。

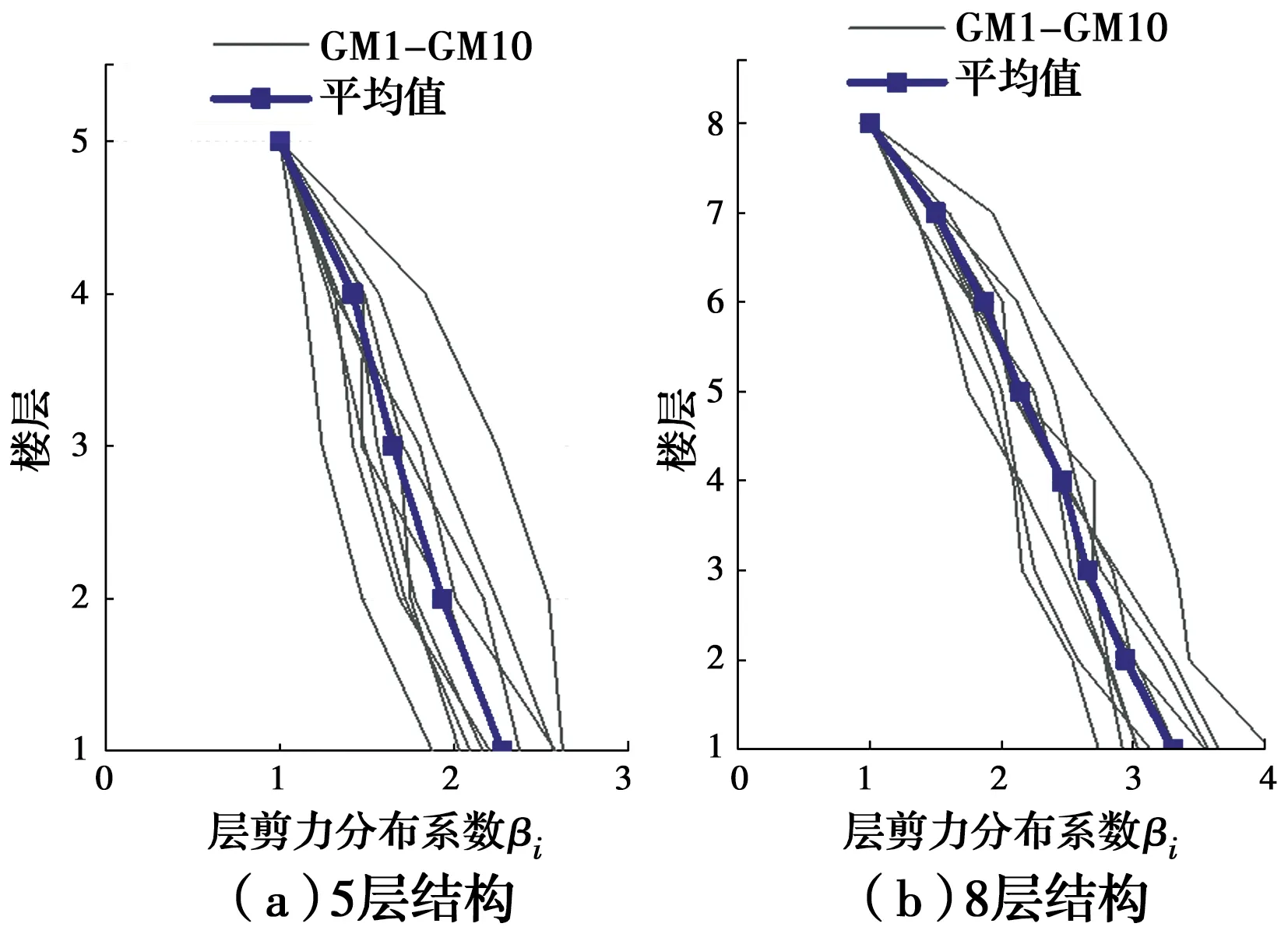
图8 不同地震动下层剪力分布系数及平均值Fig.8 Shear force distribution coefficient and average value under different ground motions

为将从优化结构提取的层剪力分布系数更好地应用于工程实践，需将其进行合理表征。不失一般性并使公式保持较好的简便性，以《建筑抗震设计规范》中的侧向力分布模式为基础[18]，对顶点附加地震作用系数δn进行重新标定，给出适用于RC框架结构抗震设计的层剪力分布简化公式。δn考虑为式(8)所示形式(a和b为系数)。

δn=aT+b

(8)

根据新的侧向力模式，可获得层剪力的计算表达式，进而获得层剪力分布系数βi的计算表达式。βi的表达式中仅有a、b两个系数需确定。基于优化结构的层剪力分布系数，采用一元线性回归方法，确定出了a=-0.238 4、b=0.506 5，最后获得δn=-0.238 4T1+ 0.506 5。为验证拟合公式的精确性和有效性，将层剪力分布系数的拟合值和优化结构的计算值作对比分析，结果如图9所示。由图9可以看出，采用新公式的拟合值整体上与计算值相近，特别是在楼层的中上部，两者的结果非常接近。8层结构的下部楼层，计算值和拟合值有一定的偏差，其主要原因在于侧向力拟合公式是基于规范格式，其拟合形式并未最优。尽管如此，拟合公式的相关系数在0.85以上，仍然具有较好的精度，能满足工程应用需求。

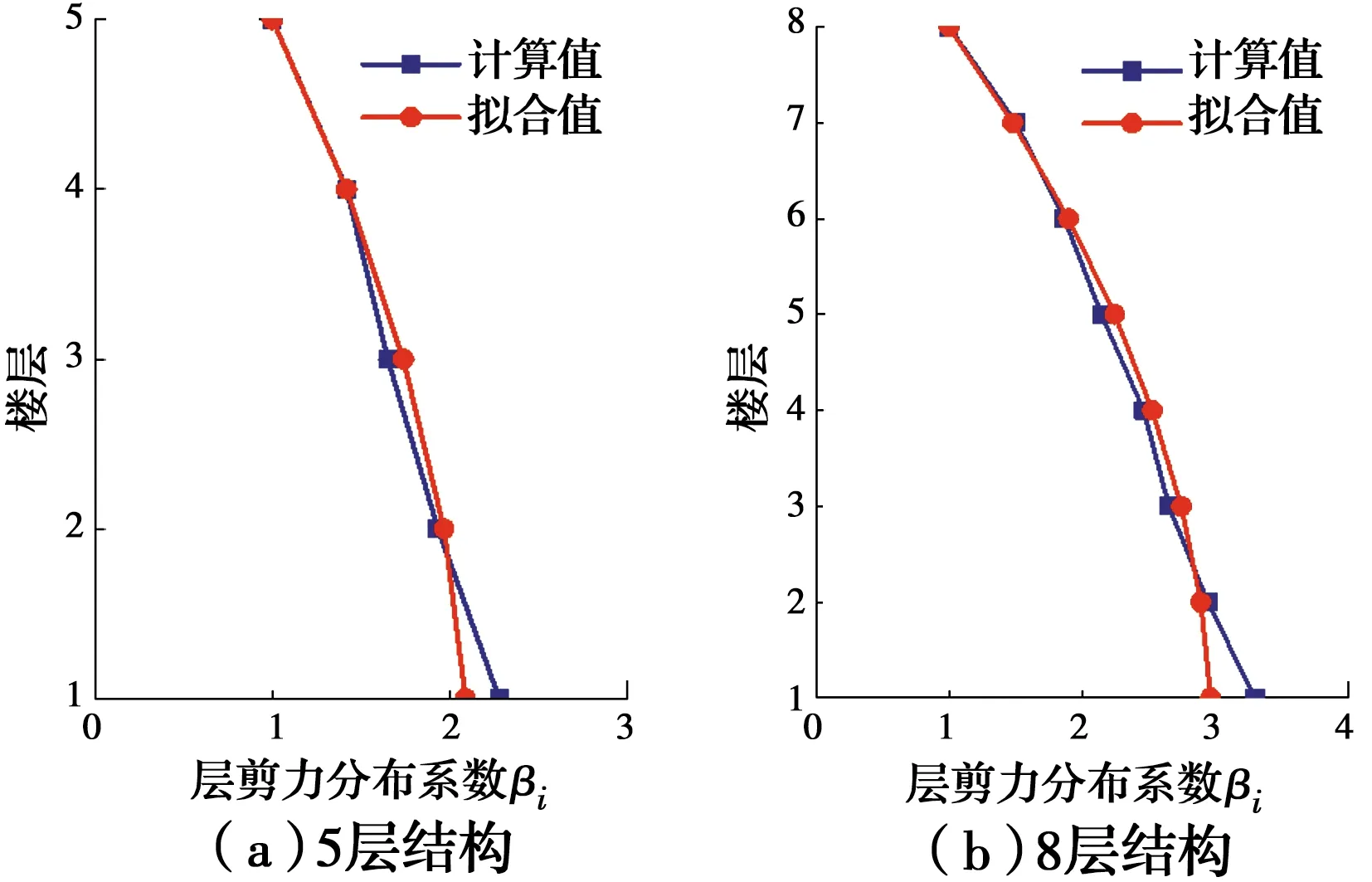
图9 层剪力分布系数计算值与拟合值对比Fig.9 Comparison of calculated values and fitted values of shear force distribution coefficient

为了解采用新型侧向力获得的层剪力分布与中国规范设计中底部剪力法获得的层剪力分布的差别，图10给出了两个结构的对比分析。由图10可以看出，由于计算公式与规范公式的形式相同，两者的曲线性状相同。此外，对于两个结构，拟合值比规范值整体偏小。需要说明的是，新型侧向力模式是针对特定结构类型、特定场地类型获得的，对于其他结构类型和计算模型，其适用性需要进一步深入研究。

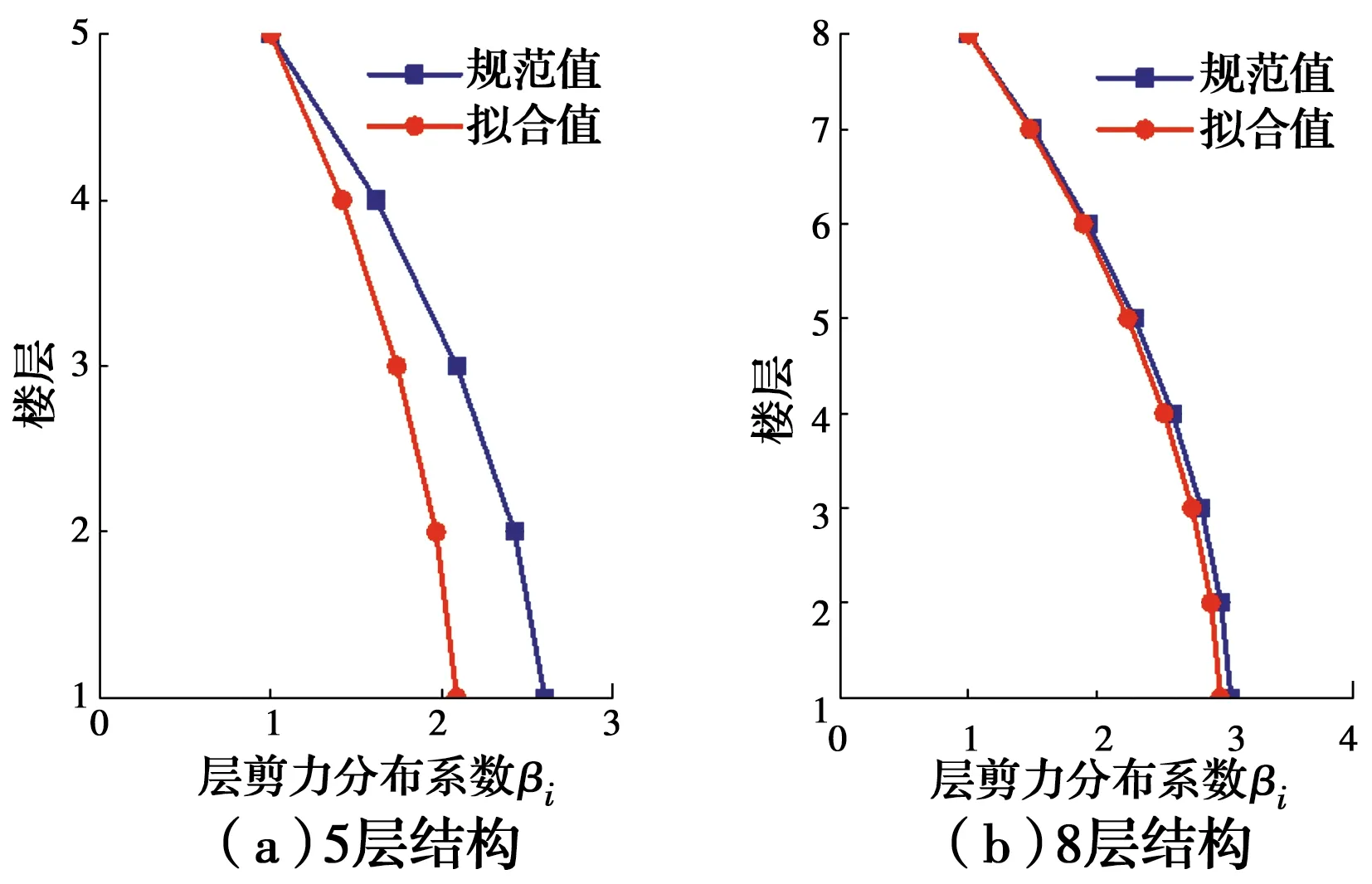
图10 层剪力分布系数规范值与拟合值对比Fig.10 Comparison of code values and fitted values of shear force distribution coefficient

5 结论

在结构均匀损伤抗震设计的基础上，提出了钢筋混凝土框架结构抗震设计的新型侧向力模式。构建了实现RC框架结构地震均匀损伤的优化程序，并以3个考虑了土-结构动力相互作用的RC框架结构为例，通过优化设计和分析，获得了结构层剪力的分布模式，并给出了新型侧向力模式的表达式。得到以下主要结论：

1)提出的均匀损伤优化算法，能直接考虑结构损伤大小(包括局部损伤与整体损伤)与结构变形模式之间的关系，且优化程序简便、易于操作。优化程序中收敛参数α、γ从收敛稳定性和收敛速度考虑，建议取值为0.2。

2)结构在均匀损伤分布时，由于实现了耗能全局化、变形均匀化，结构易于形成“强柱弱梁”的整体屈服机制，层间位移角分布更加均匀，结构的抗震性能明显提升。

3)提出的基于规范格式的RC框架新型抗震设计侧向力模式，具有良好的精确性和简便性，便于工程实际应用。