正确理解概率公式

文 王玉珍

我们在解决概率问题时，常常会因为对一些概念把握不到位，而与正确答案失之交臂。

一、使用概率公式的前提

一般地，设一个试验的所有可能发生的结果有n个，它们都是随机事件，每次试验有且只有其中的一种结果出现。如果每种结果出现的机会均等，那么我们说这n个事件的发生是等可能的，也称这个试验的结果具有等可能性。

这个概念比较抽象。细读之后我们能发现，等可能性需要同时具备三个条件：（1）n表示试验的结果是有限个；（2）都是随机事件；（3）每次试验有且只有其中的一种结果出现，并且每种结果出现的机会均等。这三个条件缺一不可。下面，我们一起来看看苏科版数学教材九年级上册第128页的例题：

一只不透明的袋子中装有1个白球和2个红球，这些球除颜色外都相同，搅匀后从中任意摸出1个球。摸到白球与摸到红球的可能性相同吗？

小明同学说：摸到的球不是白球就是红球，所以摸到白球和摸到红球这两个事件是等可能的。

小丽同学说：摸到每一个球的可能性相同，而红球有2个，白球只有1个，摸到红球的可能性大。

小明、小丽的说法哪一个正确？

【分析】我们从题目中的关键词“不透明”“这些球除颜色外都相同”“搅匀”等不难发现，摸到白球和摸到红球都是随机事件；3个球中任意摸出1个球说明试验的结果是有限种。根据试验的结果具有等可能性的定义，本试验已经具备两个条件，还缺一个条件，即每种结果出现的机会均等。因此，我们只要把2个红球编号：红球1和红球2，这样从中摸到每一个球的机会就均等了。搅匀后从中任意摸出一个球会出现3种等可能的结果：白球、红球1、红球2，所以摸到红球的可能性大。综上可见，小丽对概念的理解是到位的。

细心的同学还会发现，摸球这个典型的试验贯穿了概率的整个章节。

二、等可能条件下的概率公式

一般地，如果一个试验有n种等可能的结果，当其中的m种结果之一出现时，事件A发生。那么事件A发生的概率是P（A）=（其中m表示事件A发生可能出现的结果数，n表示所有等可能出现的结果数）。

在对月相的变化进行讲解时，单纯的依靠教材中的图片和教师的讲解，对缺乏空间思维能力的小学生而言，并不能很好的理解月球运动的特点，也就无法发现月相变化的规律，导致教学效果不明显。如果应用信息技术，教师可以从网上下载一些模拟月球运动的视频或自己动手制作演示动画，通过反复播放能将月相的变化更清晰地展示在学生面前。

细读之后，我们能发现使用概率公式的前提条件是：一个试验有n种等可能的结果，也就是试验的结果必须具有等可能性。

【拓展1】上面的例题，继续问你：摸到红球的概率是多少？

【分析】这属于一步摸球试验。我们可以先做出判断：这个试验的结果具有等可能性，然后列出所有等可能的结果，直接代入公式求解。

解：把2个红球编号为红球1和红球2。搅匀后从中任意摸出一个球会出现3种等可能的结果：白球、红球1、红球2。摸到红球1、摸到红球2这两种结果之一出现时，“摸到红球”这一事件发生，所以P（摸到红球）=。

【拓展2】我们将上面的例题改编如下：

一只不透明的袋子中装有1个白球和2个红球，这些球除颜色外都相同。搅匀后从袋中任意摸出1个球，记录颜色后放回。搅匀后再从中任意摸出1个球。求两次都摸到红球的概率。

【分析】这属于两步摸球试验。我们要先做出判断：这个试验的结果具有等可能性，然后列出所有等可能的结果，再直接代入公式求解即可。这个试验的所有等可能结果不能一眼看出，需要借助列表或画树状图进行分析。当然要想做对，还需仔细读题，“放回”是这个问题的关键词。

解：把2个红球编号为红球1、红球2，用表格列出所有可能的结果：

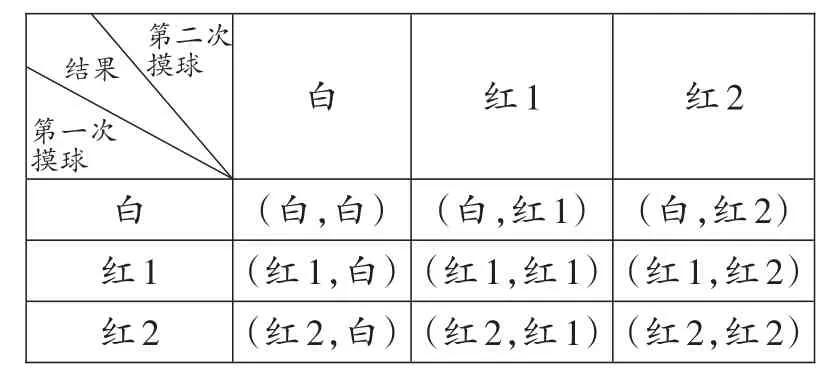
白红1红2白（白，白）（红1，白）（红2，白）红1（白，红1）（红1，红1）（红2，红1）红2（白，红2）（红1，红2）（红2，红2）结果第二次摸球第一次摸球

由表格可知，共有9种等可能出现的结果，“两次都摸到红球”的结果有4种，所以P（两次都摸到红球）=。

【拓展3】将【拓展2】的“放回”前加一个字“不”，你还能正确求出结果吗？

【分析】解答过程与【拓展2】类似，唯一不同的是第一次摸出白球，不放回，第二次摸时袋子里只有红球1和红球2，不可能摸出白球了，所以列表如下：

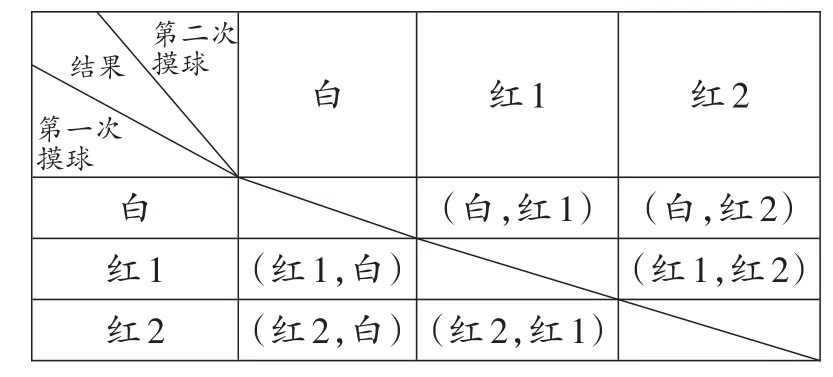
白红1红2白（红1，白）（红2，白）红1（白，红1）（红2，红1）红2（白，红2）（红1，红2）结果第二次摸球第一次摸球

【拓展4】又按照之前【拓展3】的方法再摸一次，求前两次都摸到红球，最后一次摸到白球的概率。又应该怎么做呢？

【分析】这属于三步摸球试验。我们还是要先做出判断：这个试验的结果具有等可能性，然后列出所有等可能的结果代入公式求解。我们尝试列表发现，第三步不便于书写，所以本题应借助树状图来完成。

解：把2个红球编号为红球1、红球2，用树状图列出所有可能的结果。

由上图可知，共有6种等可能的结果，其中“前两次都摸到红球，最后一次摸到白球”的结果有2种，所以P（前两次都摸到红球，最后一次摸到白球）=。