基于NSGSA的DC-DC变换器无源控制器参数多目标优化

王 康，王久和，张雅静，李 萍，陈启丽

(北京信息科技大学 自动化学院，北京 100192)

0 引言

目前，DC-DC变换器得益于直流微网、电动汽车、电气化轨道交通的发展而得到更多的应用。Boost变换器因其具有升压功能而被广泛应用于微电网中，并得到一些学者的关注[1-7]。由于Boost变换器是非线性被控对象，采用传统的线性控制方法对其进行控制具有较大的局限性[8-9]。因此，多采用反馈线性化控制、滑模控制和PBC等非线性控制方法使Boost变换器输出电压在受到内、外扰动时保持稳定。与其他非线性控制方法相比，PBC是一种本质的非线性控制方法，可实现系统大范围稳定[10-11]。该控制方法的核心思想为，在控制策略中注入合适的阻尼以控制系统能量渐进收敛到期望值，从而使系统的状态迅速达到期望平衡点，达到快速、精确跟踪的目的。目前，将PBC应用于带恒功率负载的DC-DC变换器使其输出电压得到稳定控制的研究较多，且控制效果显著[12-15]。

但是，目前对于PBC控制器参数确定方法的研究较少。文献[16]以Buck变换器和Boost变换器为例，提出了通过Brayton-Moser (BM) 方程所表示的系统稳定约束条件[17]，得到控制器参数调整范围。该方法需要将系统的EL模型转换为BM方程，所采用的稳定约束条件比较保守，只能得到参数调整范围的下界。文献[18]以PBC控制的Buck变换器为研究对象，提出了一种通过数值计算确定控制器最优参数的方法。该方法在静态工作点处建立系统传递函数，通过校正电感电流超调量得到注入阻尼值取值范围，并基于此取值范围将输出电压误差作为优化目标，使用遗传算法确定最优注入阻尼值。该方法不足之处在于使用小信号分析法来研究非线性控制问题且未考虑扰动工况对系统的影响。

因此，本文以基于EL模型的PBC控制的Boost变换器为例，通过增加一个能量控制外环获得一个实时的期望电感电流，使Boost变换器在受扰工况下的输出电压依然保持稳定，从而使PBC具有一定鲁棒性。由于该控制器内环有注入阻尼、外环有比例和积分系数这3个参数，它们相互影响，仅依赖经验无法得出最佳参数值。对此，本文提出在Boost变换器闭环系统中加入改进的LSINSGSA优化控制器参数，改进算法的收敛性与最优解集均匀分布性在原算法NSGSA基础上得到进一步提升，最终取得了满意的参数优化效果。该方法的适用对象不只限于Boost变换器，也可推广到其他DC-DC变换器中。

1 Boost变换器EL模型

Boost变换器主电路如图1所示。E为直流输入电源电压，L为电感器电感，C为输出电容器电容，R为负载电阻，VD为二极管，VT为开关管，u为输入控制量，iL为一个开关周期内流过电感器的平均电流，uC为一个开关周期内输出电容器两端的平均电压。

图1 Boost变换器主电路Fig.1 Power circuit of boost converter

假设图1中的元器件均为理想器件，并考虑该电路工作在连续导通模式，可得电路的动态方程

(1)

式中，μ为占空比。

式(1)的EL模型为

(2)

2 无源控制器设计

2.1 无源性定义

考虑一个m输入m输出系统

(3)

式中，x∈Rn为状态，u∈Rm为输入，y∈Rm为输出且关于x连续，f是局部Lipschitz的。

对于系统(3)，若存在连续可微半正定函数H(x)，使得不等式

(4)

对∀(x,u)∈Rn×Rm成立，则系统是无源的[19]。

下面对带电阻负载的Boost变换器的无源性进行研究。

对于式(2)，取正定函数为

(5)

则H(x)对时间的导数为

(6)

由于RB为正定矩阵，由式(6)可得

(7)

当取Boost变换器的状态变量x为输出y时，由无源性定义可知式(2)所示的Boost变换器是无源的，可对其进行无源控制器设计。

2.2 无源控制器设计

(8)

Step1：注入阻尼Ra

(9)

Step2：能量成型

令式(9)等号右边为零可得无源控制律

u=(J+RB)x*-Raxe,

(10)

取误差能量存储函数为

(11)

则H(xe)对时间的导数为

(12)

由式(10)可得

(13)

(14)

(15)

本文内环采用PBC控制，可通过选取适当的注入阻尼值来抑制起动阶段的冲击电流，因此无须额外的滤波装置，易于工程实现。

结合式(14)和式(15)，可得改进的PBC控制器框图如图2所示。图中rL、rC分别为电感器的等效电阻和输出电容器的等效串联电阻。

图2 PBC控制器框图Fig.2 PBC controller block diagram

改进的PBC控制器包含Ra1、k1和k2这3个参数，由于内、外环控制的关系，这3个参数相互耦合，仅依赖经验公式法并不能得到最佳整定参数值。因此，本文对NSGSA算法进行改进，并用改进的NSGSA算法优化PBC控制器参数。

3 无源控制器参数多目标优化

NSGSA算法具有比非支配排序遗传算法Ⅱ(Non-dominated Sorting Genetic Algorithm，NSGAⅡ)等多目标优化算法更快的收敛速度、更均匀的最优解集分布[21-22]。对于含3个及以上目标函数的多目标优化问题，NSGSA解的收敛性与均匀分布性能仍有很大的提升空间。本文基于NSGSA算法提出一种改进的NSGSA，即LSINSGSA。该算法能够有效求解含3个及以上目标函数的多目标优化问题。改进的NSGSA算法可显著提升原有算法的收敛速度与最优解集的均匀分布性能。

3.1 改进的NSGSA算法

3.1.1 改进的存档维护策略

距离帕累托前沿较近的粒子加入到移动粒子列表中可加快其他粒子向帕累托前沿收敛的速度，因此在维护存档长度时需要同时考虑到粒子的收敛性与分布性。而NSGSA的存档维护策略仅依赖最优解集均匀分布指标，这往往会删除收敛性较好的粒子。文献[23]考虑将粒子收敛性与分布性二者融合成为一个指标，即双性能测度指标，对存档长度进行维护。受文献[23]启发，本文提出类似的收敛性与均匀分布性融合指标，将全局损害与粒子势能[24]的动态加权和作为粒子收敛性评价指标，将粒子的拥挤距离作为粒子均匀分布评价指标，二者比值即为平衡粒子收敛性与均匀分布性的融合指标。相关公式定义如下：

假设优化目标个数为M，存档中的实时粒子个数为K，则存档中第i个粒子pi的势能PT计算方法为

(16)

存档中粒子pi的全局损害GD为[23]

(17)

式中，fj,m为粒子pj的第m个目标函数值。GD指标反映了粒子对全局收敛性的损害程度，GD越大表示粒子对于当前所有粒子总体收敛情况的损害程度越大。

存档中粒子pi的收敛度CD为

(18)

式中，Tg表示第g次迭代，Th为迭代前期与后期分界标志。由CD指标计算公式可知，迭代早期更注重粒子加速向势能低的方向运动，接近迭代后期时由于粒子已经接近真实帕累托前沿，因此逐渐增加GD指标的权重以淘汰全局损害较大的粒子，增加粒子的收敛精度。此外，粒子的收敛度CD越小，表明粒子当前的收敛性越好，反之，则收敛性越差。

考虑到存档中粒子在多维目标空间中均匀分布，本文采用距离粒子pi最近的S个粒子到该粒子的欧氏距离之和的平均作为粒子pi的拥挤距离，拥挤距离LD计算公式如下

(19)

上式表明，粒子的拥挤距离LD越大，则粒子在多维目标空间中越不拥挤。

平衡粒子收敛性与均匀分布性的融合指标CED为

(20)

由上式可知，当粒子的收敛度CD越小、拥挤距离LD越大，融合指标CED就越小，即表明粒子的综合性能越优越，在多维目标空间中越接近真实的帕累托前沿且在该空间中分布越均匀。当存档中的粒子个数超出存档长度时，从CED最大的粒子开始依次删除多余的粒子对存档进行维护。对比NSGSA算法仅依赖均匀分布性指标维护存档，本文提出的兼顾粒子收敛性与均匀分布性的融合指标CDE在保持粒子均匀分布性的同时能够对收敛性较好的粒子进行保留，如果将其加入到移动粒子列表中，将有益于提高全局收敛速度。

3.1.2 改进的位置更新策略

NSGSA采用符号变异与坐标变异策略更新移动列表中粒子的位置，以防止粒子陷入局部最优。但是，经符号变异与坐标变异后的粒子可能会退化。针对该问题本文提出退步策略，即位置更新后的粒子如果被位置更新前的粒子支配，则保持该粒子当前位置为更新前的位置，否则，粒子当前位置为经符号变异与坐标变异更新后的位置。粒子退步公式如下:

(21)

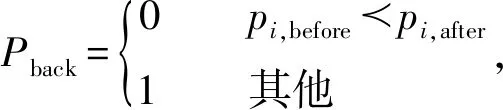
(22)

3.1.3 改进的KBEST策略

为了避免陷入局部最优情况，NSGSA沿用GSA中的KBEST策略，即移动粒子列表中只有Kbest个粒子对其他粒子有引力作用，且Kbest是一个初始值为最大移动粒子列表长度的并随迭代次数增加而递减的函数，最终只有一个粒子对其他粒子有引力作用。该策略的不足在于，在最后几次迭代中的少数Kbest粒子会破坏全局收敛程度以及非支配解的均匀分布性。对此，本文提出在迭代后期Kbest由M个极端粒子和M个最不拥挤粒子组成，以保持迭代后期最优的全局收敛程度以及最优的非支配解均匀分布性。Kbest表达式如下

(23)

式中，Nmov为实际的移动粒子列表个数，且Nmov不大于最大移动粒子列表个数。

3.1.4 改进的精英策略

NSGSA采取精英策略随机选取存档中的粒子加入到移动粒子列表中吸引其他粒子运动。为了加快全局收敛，本文提出在迭代前期将势能小的粒子加入到移动粒子列表吸引势能大的粒子向帕累托前沿加速靠近，后期则将势能大的粒子加入到移动粒子列表中让其受到极端粒子和最不拥挤粒子的吸引，加快迭代后期的全局收敛速度并提高最优解集均匀分布水平。此外，由于陷入局部最优的情况发生在迭代早期，为了加快后期的收敛速度，故在迭代后期对非极端粒子和非最不拥挤粒子的位置更新不采取符号变异和坐标变异策略；为了实际帕累托前沿接近理论上的帕累托前沿且获得最优解集分布均匀最大化，对极端粒子和最不拥挤粒子仍采取符号变异与坐标变异策略。

改进算法的操作步骤如下：

1)初始化LSINSGSA算法的迭代次数、粒子个数、存档长度等参数，随机初始化所有粒子的位置并将所有粒子的初始速度和加速度都设置为零，将初始位置代入到多目标函数中得到粒子的初始多目标函数值。

2)对移动粒子列表中的粒子进行非支配排序，并采用改进的融合指标维护外部存档长度。

3)基于改进的精英策略与最不拥挤粒子选取方法更新移动粒子列表。

4)基于粒子等级计算移动粒子的适应度值。

5)计算移动粒子的质量，并基于改进的KBEST策略计算移动粒子受到的引力和加速度。

6)计算移动粒子的速度并基于退步策略更新移动粒子的位置，该步骤包括计算更新后粒子的多目标函数值。

7)如果当前迭代次数未达到最大迭代次数，则依次重复步骤2)～6)；否则，退出循环，返回存档中的粒子信息。

LSINSGSA算法流程如图3所示。

图3 LSINSGSA算法流程图Fig.3 Algorithm flowchart of LSINSGSA

以三维目标测试函数DTLZ2为例，对改进的NSGSA算法进行测试，并与原有的NSGSA算法、NSGAII算法比较。算法实验平台：Windows10操作系统，Intel Core i7 8700K CPU，32G内存台式机，采用MATLAB语言编程。算法参数设置为：三者的种群大小与外部存档长度均为100，终止迭代次数为250次；Th=220，S=3，LSINSGSA的其他参数设置与NSGSA相同，NSGAII算法参数同文献[25]。LSINSGSA、NSGSA、NSGAII三者在DTLZ2测试函数下的测试结果如图4所示。

图4 LSINSGSA、NSGSA、NSGAII的DTLZ2测试结果Fig.4 DTLZ2 test results of LSINSGSA, NSGSA, NSGAII

从图4可知，LSINSGSA的粒子很好地收敛于帕累托最优前沿且分布均匀，其收敛性与最优解集均匀分布性均优于NSGSA和NSGAII算法。因此，LSINSGSA在收敛速度得到提高的同时其最优解的多样性也获得明显地提升，实现了最优解不遗漏，保证了有效求解含有3个及以上目标函数的多目标优化问题。

3.2 多目标函数定义

为了使优化后的参数能够让控制器具备所期望的良好性能，需要对多目标函数进行相应的定义。对于DC-DC变换器的控制，主要关注其起动阶段的电流与电压的超调量、上升时间、调节时间和静态时输出电压误差与纹波大小等性能指标。

对于一个控制系统的性能优劣，常用误差积分准则来评价。目前，误差积分准则主要有平方误差积分准则(Integral of Squared Error，ISE)、时间乘平方误差积分准则(Integral of Time Weighted Squared Error，ITSE)、绝对误差积分准则(Integral Absolute Error，IAE)、时间乘绝对误差积分准则(Integral of Time Weighted Absolute Error，ITAE)。其中，ITAE的瞬态响应能力优于其他误差积分准则，可作为表征系统上升时间和调节时间的目标函数[26]。在一组最优解中，输出电压的超调量、静态误差与纹波大小可统一由一个目标函数来表征。电流超调量由最大电感电流值函数表征。因此，可设定3个目标函数表征以上各性能指标，目标函数定义如下：

(1)ITAE

(24)

式中，D为设定的仿真时长。

(2)综合输出电压的超调量、静态误差与纹波大小的目标函数|ΔuC|

(25)

式中，uC,i为D时间内的实际输出电压，N为D时间内总采样点数。

(3)最大电感电流iLmax

iLmax=max{iL,i}i=1,2,…,N

，

(26)

式中，iL,i为D时间内的实际电感电流。

因此，控制器参数多目标优化函数为

(27)

式中，aj、bj、cj(j=1,2)为常量。

3.3 最优参数确定

基于LSINSGSA的PBC控制系统参数优化结构如图5所示。LSINSGSA参数见表1，主电路参数见表2。

图5 参数优化框图Fig.5 Parameter optimization block diagram

表1 LSINSGSA参数表Tab.1 Parameters of LSINSGSA

表2 主电路参数表Tab.2 Parameters of power circuit

按表1及表2 所给参数，优化控制器参数。最大迭代次数设为100，可得到一组Pareto最优解集，如图6所示。依据灰色关联分析法[27]及电感电流超调量取值应在1.5%～25.4%内，得到部分最优解如表3所示。

由表3可知，第2组的ITAE值最小，表明其动态响应速度最快，但同时它的|ΔuC|值最大，表明其电压超调最大。第1组和第2组的iLmax值相近且都较大，表明它们的电感电流超调较大，但都在合理范围内。相较于第1组和第2组，第3组的iLmax值较小，表明其在起动阶段的电感电流超调较小。由灰色关联分析法可知，如果某组可行方案的灰色关联度越大，则表明该组方案的综合实施效果最好。表3中的第1组目标函数的灰色关联度最大，则采用该组参数的控制器其综合控制效果最好，该结果符合上述分析。

图6 最优解集Fig.6 Optimal solution set

表3 最优解列表Tab.3 Optimal solution list

4 仿真验证

为了验证参数优化后的无源控制器的优越控制性能，对表3中前三组的参数进行仿真验证。仿真在两种工况下进行，即工况1和工况2，其定义分别如下：

工况1：Boost变换器在输入电压与负载都不存在扰动情况下其输出电压达到期望值后，在0.3 s时刻，输入电压下降10%，由100 V下降为90 V；之后，在0.6 s时刻，负载电阻增加25%，由20 Ω增加至25 Ω。

工况2：Boost变换器在输入电压与负载都不存在扰动情况下其输出电压达到期望值后，在0.3 s时刻，输入电压上升10%，由100 V上升为110 V；之后，在0.6 s时刻，负载电阻减少25%，由20 Ω减少至15 Ω。

采用前三组参数的Boost变换器在工况1、工况2下的仿真结果分别如图7、图8所示。相应工况下的各组性能指标见表4、表5，表中Δuc为各工况下各阶段的期望输出电压与实际输出电压的最大值或最小值的差值，其符号“+”、“-”分别表示电压上升或下降，ts为调节时间。

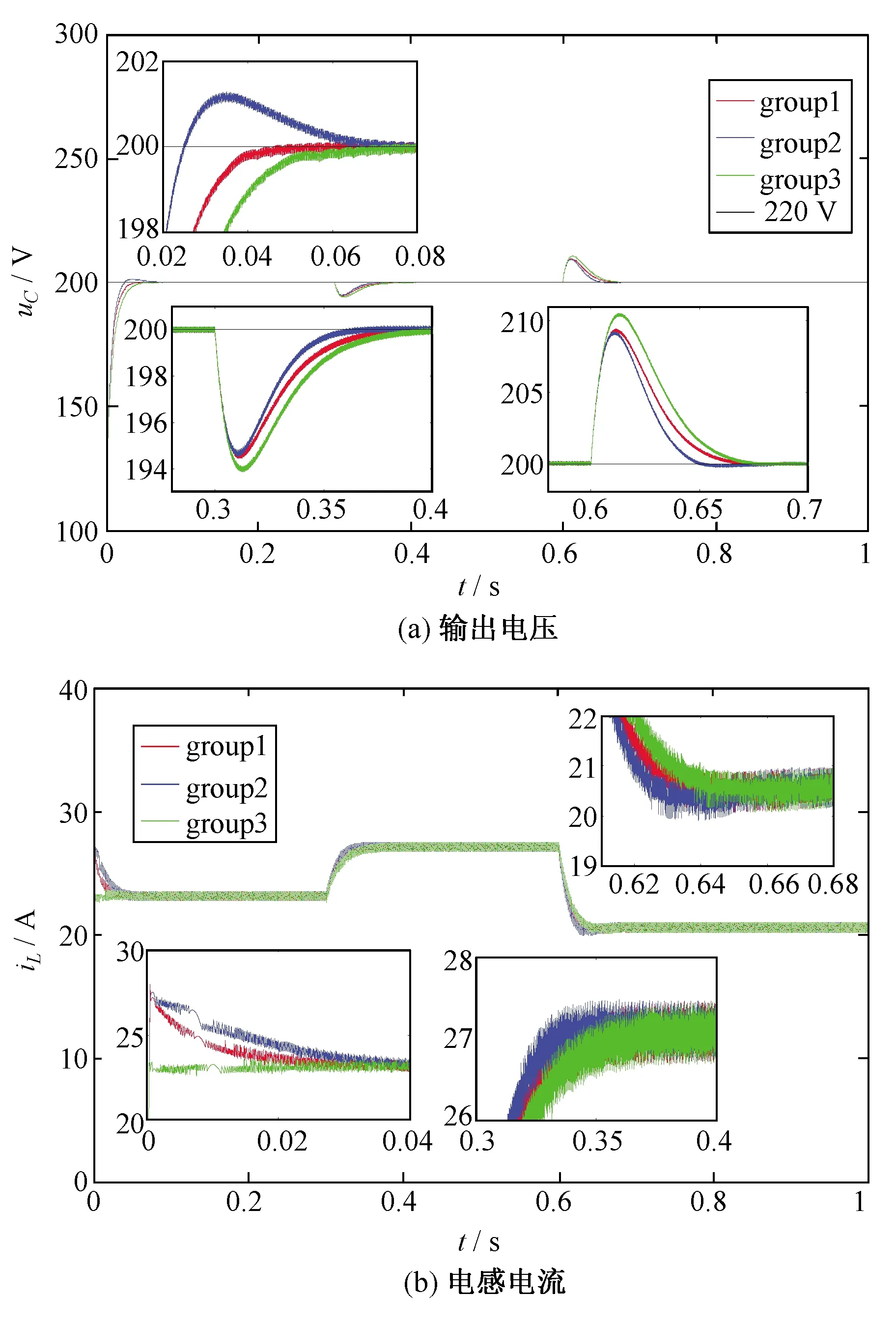
图7 工况1下的输出电压与电感电流Fig.7 Output voltages and inductor currents under working condition 1

图8 工况2下的输出电压与电感电流Fig.8 Output voltages and inductor currents under working condition 2

由图7、图8并结合表4、表5可知，在起动阶段第1组的控制器的控制性能优于其他两组，在扰动阶段第1组与第2组的抗扰能力与电压恢复能力相近且明显优于第3组。同时可得，ITAE越小，系统受扰后的电压恢复能力越强，但是在起动阶段其输出电压可能会超调，这与本文3.3部分的分析一致。

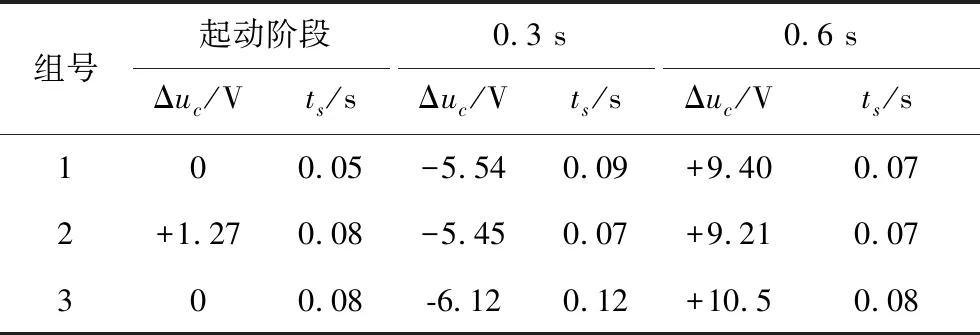
表4 工况1下各组性能指标Tab.4 Performance indicators of each group under working condition 1

表5 工况2下各组性能指标Tab.5 Performance indicators of each group under working condition 2

综上，第一组的控制器的综合性能是最优的，这也表明本文所提出的参数优化方法是可行且有效的，易于从众多可行方案中选取综合性能最优的方案，能够很好地解决无源控制器参数不易整定的问题。

5 结论

本文对PBC控制器参数不易整定的问题，提出了使用改进的NSGSA算法，即LSINSGSA算法优化控制器参数的方法。基于定义的能够表示超调量、静态误差、上升时间以及调节时间的三个目标函数，在Boost变换器闭环系统中加入改进的LSINSGSA算法进行参数寻优。同时，采用多种策略对NSGSA算法进行改进，进一步提高了原算法NSGSA的收敛速度与最优解集均匀分布水平，克服原有算法不能有效求解三维及以上的多目标优化问题。通过仿真验证，经LSINSGSA算法寻优得到的控制器参数可使变换器输出电压在起动阶段无超调、响应快速，在稳态阶段无静差，在扰动工况下电压恢复能力强，验证了本文所提出的基于改进的LSINSGSA算法优化PBC控制器参数方法的可行性和便捷性。