基于笛卡尔积构造时频二维部分周期低碰撞区跳频序列集
许成谦,李伟杰,徐 琪,惠 中
(1.燕山大学 信息科学与工程学院,河北 秦皇岛 066004;2.秦皇岛鸿泰科技股份有限公司,河北 秦皇岛 066000)
0 引言
跳频通信系统自诞生至今,通过使用一组性能良好的跳频序列(Frequency Hopping Sequence,FHS),实现了抗干扰和反拦截功能,被广泛应用于信号传输等领域。通过跳频通信系统进行信号传输时,时延和多普勒频移会导致信号的错位、频率色散等,使得接收端获取错误的信息。所以需要考虑序列时频移位不等价性以及考虑频域非周期移位的时频二维部分周期(Two-Dimensional Partial Period of Time-Frequency,TF-TDPP)Hamming相关函数,并将其应用于衡量新构造的笛卡尔积跳频序列集(Frequency Hopping Sequence Set,FHSS)的性能。
为了提高信号检测速度,常常分析跳频序列的部分相关性。对相关跳频序列的研究主要包括理论界和构造方法两个方面。文献[1-6]给出了传统一维的理论界,为评判后续研究生成序列的性能提供了标准。文献[7]证明了区组与单一FHS之间的关系,给出了几种FHS的直接构造方法。文献[8]构造了部分周期相关FHSS,通过一维部分周期Hamming相关函数的分析,满足Lempel-Greenberger 界,得出其Hamming相关性最优。文献[9]借助笛卡尔积的数学思想,提出了构造周期低碰撞区(Low Hit Zone,LHZ )FHS的理论,将多个Solomon FHSS进行笛卡尔积或多个Solomon FHSS、Kumar FHSS进行笛卡尔积得到Hamming相关性最优的FHSS。文献[8-9]是将满足构造方法的原始FHSS通过交织、进行笛卡尔积间接构造出FHSS。由于注意到多普勒频移带来的影响,人们开始研究既有时延又有频移的时频二维Hamming相关FHSS。文献[10]导出了FHSS的LHZ TF-TDPP Hamming相关函数的理论界。文献[11]通过将Welch Costas FHS和Golomb Costas FHS采样得到了时频二维Hamming相关性能最优的两类FHSS。文献[12]将传统的笛卡尔积数学思想应用到了时频二维非周期FHSS的构造方法中,得到了近似最优的笛卡尔积LHZ FHSS。文献[13]针对先前一维Hamming相关性最优的Cai FHSS进行了TF-TDPP Hamming相关性分析,得到了Cai FHSS达到性能最优的条件。
将笛卡尔积数学理论应用于FHSS已有很多成果。早期的文献[9]构造了性能最优的笛卡尔积LHZ FHSS。随后,文献[14]给出了构造传统一维部分周期笛卡尔积LHZ FHSS,并通过原始FHSS的参数限制衍生出3种新的构造步骤。文献[15]构造了传统一维的在最大部分周期性能最优的笛卡尔积LHZ FHSS。文献[16]通过将两类FHSS笛卡尔积得到了一类一次碰撞的笛卡尔积LHZ FHSS。
本文首先证明多个频隙集上FHS笛卡尔积具有的性质,然后提出一种构造笛卡尔积FHSS的方法。最后分析Cai FHSS的频域非周期移位TF-TDPP Hamming相关性,将Cai FHSS用于新构造方法中得到数量更多、长度更长的笛卡尔积LHZ FHSS。
1 相关概念

定义2设S是跳频序列集,Ha,Hc,TA,VA为非负整数,令
LPAHt(S)=max{TA|Ha,a(τ,f;k|W)≤Ha,∀a∈S,0≤τ≤TA,0≤f≤VA,(τ,f)≠(0,0)},
LPAHf(S)=max{VA|Ha,a(τ,f;k|W)≤Ha,∀a∈S,0≤τ≤TA,0≤f≤VA,(τ,f)≠(0,0)},
LPCHt(S)=max{TA|Ha,b(τ,f;k|W)≤Hc,∀a,b∈S,0≤τ≤TA,0≤f≤VA,a≠b},
LPCHf(S)=max{VA|Ha,b(τ,f;k|W)≤Hc,∀a,b∈S,0≤τ≤TA,0≤f≤VA,a≠b},
LPHt(S)=min{LPAHt(S),LPCHt(S)},
LPHf(S)=min{LPAHf(S),LPCHf(S)}。
若(LPHt(S),LPHf(S))≠(0,0),则[0,LPHt(S)]×[0,LPHf(S)]称为S的频域非周期移位的TF-TDPP Hamming相关LHZ,[0,LPAHt(S)]×[0,LPAHf(S)]、[0,LPCHt(S)]×[0,LPCHf(S)]分别称为S的频域非周期移位的TF-TDPP Hamming自相关LHZ和互相关LHZ,则LHZ 跳频序列集S的参数为(N,M,q,LPHt,LPHf,W,Ha(S),Hc(S))。当Hm(S)=max{Ha(S),Hc(S)}时,S的参数也记为(N,M,q,LPHt,LPHf,W,Hm(S))。
定义3设有I个非空集合B0,B1,…,BI-1,称集合B0×B1×…×BI-1={(x0,x1,…,xI-1):x0∈B0,x1∈B1,…,xI-1∈BI-1}为B0,B1,…,BI-1的笛卡尔积。
定义4设a,b是任意选取的两个长度为N的跳频序列,且a≠b,若满足Ha,b(τ,f;0|N) 引理1[18]设跳频序列集S的参数为(N,M,q,LtLf,W,Hm),Hm=max{Ha,Hc},Ha,Hc分别是S最大的TF-TDPP Hamming自相关值和互相关值,则有 若S的各参数使得上式等号成立,则S是最优的。 引理1中的TF-TDPP Hamming相关函数为频域周期移位。本文定义1中的TF-TDPP Hamming相关函数为频域非周期移位。 推论1设Hmax为定义1意义下频域非周期移位的TF-TDPP异项Hamming自相关值和互相关值的最大值,Hm为引理1中要求的值,则 Hmax≤Hm。 下面给出笛卡尔积的TF-TDPP Hamming相关函数性质。 a(t)=(a1(t1),a2(t2),…,aI(tI)), b(t)=(b1(t1),b2(t2),…,bI(tI)), 当且仅当gcd(N1,N2,…,NI)=1时,等号成立。Wi为选取ai,bi的窗长度,W为选取的新构造的跳频序列a,b的窗长度,W=lcm(W1,W2,…,WI);ki为ai,bi的窗的起点,k为a,b的窗起点,ki=kmodNi,i=1,2,…,I。 证明首先,I=2,W1=n1d,W2=n2d,gcd(W1,W2)=d,W=W1n2,0≤W1≤N1,0≤W2≤N2,i=1,2,则笛卡尔积跳频序列a,b的频域非周期移位TF-TDPP Hamming相关函数描述如下: Ha,b(τ,f;k|W)= b2(t2+τ))+f]= b2(t2+τ)+f)]。 由于Ha,b(τ,f;k|W)的数值等于方程(a1(t1),a2(t2))=(b1(t1+τ)+f,b2(t2+τ)+f)的解的个数,(a1(t1),a2(t2))=(b1(t1+τ)+f,b2(t2+τ)+f)等价a1(t1)=b1(t1+τ)+f且a2(t2)=b2(t2+τ)+f,所以有 Ha,b(τ,f;k|W)= b2(t2+τ)+f)]= (a2(t1+t2W),b2(t1+t2W1+τ2)+f2)]= 由于n2≤W2,所以 当gcd(N1,N2)=1时,等号成立。 其次,假设i=1,2,…,I-1时,有 当gcd(N1,N2,…,NI-1)=1时,等号成立。 最后,当i=1,2,…,I时,有 Ha,b(τ,f;k|W)= (b1(t1+τ),b2(t2+τ),…,bI(tI+τ))+f]≤ 当gcd(N1,N2,…,NI)=1时,等号成立。 证毕。 下面给出笛卡尔积跳频序列集的构造方法,并给出构造方法结果的证明。 构造方法: 步骤2: 设N=lcm(N1,N2,…,NI),M=M1·M2…MI,对于t=0,1,…,N-1,ti≡tmodNi,i=1,2,…,I,j=1,2,…,M,ji≡jmodMi,取 cj(t)=(a1j1(t1),a2,j2(t2),…,aI,jI(tI)), 定理1跳频序列集C的参数为(N,M,q,W-1,q-1,W,λ),其中N=lcm(N1,N2,…,NI),M=M1·M2…MI,q=q1·q2…qI,W=lcm(W1,W2,…,WI),λ=λ1·λ2…λI。 证明显然N=lcm(N1,N2,…,NI),M=M1·M2…MI,W=lcm(W1,W2,…,WI)。由于跳频序列集C所在频隙为F1×F2×…×FI,所以q=q1·q2…qI。对序列集C中任意跳频序列cj,cj′,当j=j′且(τ,f)=(0,0)时,Hcj,cj′(τ,f;k|W)=W。 当j≠j′时,由引理2可得,当(τ,f)∈[0,W-1]×[0,q-1]时,TF-TDPP互相关Hamming相关函数值为 。 即 Hcj,cj′(τ,f;k|W)≤λ1·λ2…λI, 又由于λ=λ1·λ2…λI,所以Hcj,cj′(τ,f;k|W)≤λ。 当τ=W时,Hcj,cj′(τ,f;k|W)=W。 所以选取低碰撞区为(τ,f)∈[0,W-1]×[0,q-1],则得TF-TDPP互相关Hamming相关函数值为Hcj,cj′(τ,f;k|W)≤λ。 证毕。 下面对Cai跳频序列集的频域非周期移位的TF-TDPP Hamming相关性进行分析,为使用上述构造方法构造笛卡尔积跳频序列集提供了支持。 定理2设α为有限域GF(q)的本原元,q=pn,p为素数,n为正整数,β0,β1,…,βpn-1-1为GF(q)中pn-1个元素,则将跳频序列集描述如下: Hdi,di(τ,f;k|W) D中di和dj的频域非周期移位TF-TDPP Hamming互相关值为 证明对于di,dj∈D,由定义1知 Hdi,dj(τ,f;k|W)= 首先,当i=j时,对D的频域非周期移位的TF-TDPP Hamming自相关性分析如下: Hdi,di(τ,f;k|W)= 当τ=0,f=0时,显然Hdi,di(τ,f;k|W)=W。 当τ=0,f≠0时,显然Hdi,di(τ,f;k|W)=0。 当τ≠0,f=0时,此时为传统的一维Hamming自相关函数,由文献[17]知此时Hdi,dj(τ,f;k|W)≤「W/q⎤。 当τ≠0,f≠0时,有以下两种情况: 2) 当τ2=0时,由于τ=τ1+pτ2,所以τ=τ1,则有 当τ1=f时,显然得Hdi,di(τ,f;k|W)=W。 当τ1≠f时,显然得Hdi,di(τ,f;k|W)=0。 综上所述,D中FHSdi的频域非周期移位TF-TDPP Hamming自相关值为 Hdi,di(τ,f;k|W) 其次,当i≠j时,对D的频域非周期移位的TF-TDPP Hamming互相关性分析如下: Hdi,dj(τ,f;k|W)= 当τ=0,f=0,显然为传统一维Hamming互相关值,Hdi,dj(τ,f;k|W)=0。 当τ=0,f≠0,显然当βi-βj-f≠0,Hdi,dj(τ,f;k|W)=0,反之Hdi,dj(τ,f;k|W)=W。 当τ≠0,f=0,此时为传统的一维Hamming互相关函数,此时Hdi,dj(τ,f;k|W)=「W/q⎤。 1)τ2=0,若βi-βj-f-τ1=0,Hdi,dj(τ,f;k|W)=W;若βi-βj-f-τ1≠0,Hdi,dj(τ,f;k|W)=0。 2)τ2≠0,若βi-βj-f-τ1=0,Hdi,dj(τ,f;k|W)=0;若βi-βj-f-τ1≠0,Hdi,dj(τ,f;k|W)=「W/q⎤。 综上所述,D中di和dj的频域非周期移位的TF-TDPP Hamming互相关值 由于Hdi,dj(τ,f;k|W) 证毕。 构造实例: 步骤1: 取有限域F32,由定理2得到序列长为24,频隙数为9,序列数为3的跳频序列集为 d1=(7,2,8,4,1,4,3,3,1,5,4,0,6,0,2,2,6,3,0,8,7,8,5,5), d2=(0,7,5,3,8,3,6,6,8,1,3,2,4,2,7,7,4,6,2,5,0,5,1,1), d3=(2,0,1,6,5,6,4,4,5,8,6,7,3,7,0,0,3,4,7,1,2,1,8,8), 令汉明相关窗长度为5,频域非周期移位的TF-TDPP Hamming相关值为2。 选取有限域F5,由定理2得到序列长度为20,频隙数为5,序列数为1的跳频序列集为 z=(0,4,1,3,3,0,3,2,1,1,0,1,4,2,2,0,2,3,4,4)。 令汉明相关窗长度为4,频域非周期移位的TF-TDPP Hamming相关值为2。 步骤2: 将步骤1的两个跳频序列集进行笛卡尔积,得到的跳频序列集C如下: c1=((7,0),(2,4),(8,1),(4,3),(1,0),…),c2=((0,0),(7,4),(5,1),(3,3),(8,0),…),c3=((2,0),(0,4),(1,1),(6,3),(5,0),…), 由定理1知,得到的序列集C是序列长度为120,序列个数为3,低碰撞区为[0,19]×[0,44]的跳频序列集。在汉明相关窗长度为20时,Hcj,cj′(τ,f;k|W)≤3,小于步骤1中两个跳频序列集的频域非周期移位的TF-TDPP Hamming相关值的乘积2×2=4。由引理1和推论1知跳频序列集C没达到最优,但是跳频序列集C的Hamming相关性还是比较好的。 本文提出了时频移位不等价和频域非周期移位的TF-TDPP Hamming相关函数的概念,给出了一种笛卡尔积LHZ跳频序列集的构造方法。通过分析一些跳频序列集的频域非周期移位的TF-TDPP Hamming相关性找出了一类可用于该构造方法的Cai跳频序列集。2 基于笛卡尔积构造低碰撞区跳频序列集



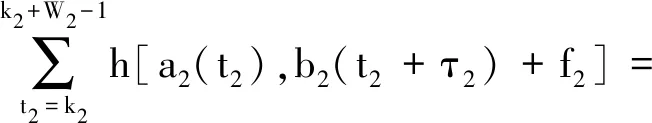
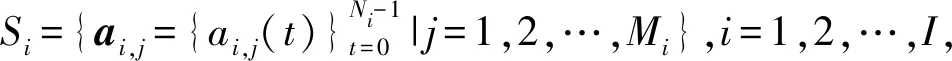




3 Cai跳频序列集的频域非周期移位的TF-TDPP Hamming相关性分析




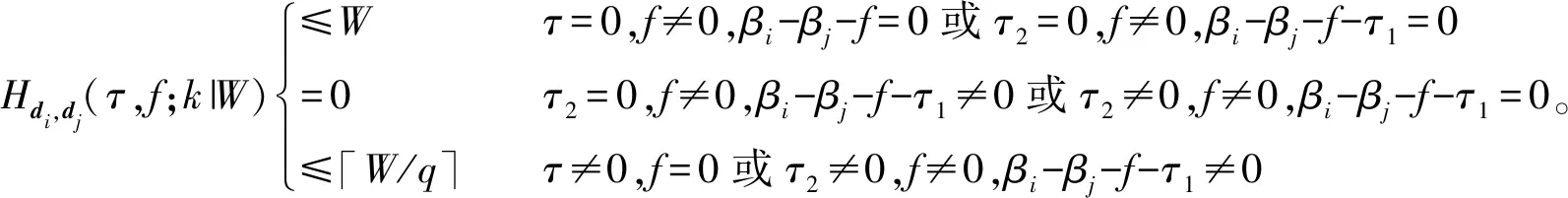
4 结论

