推挽式双向DC/DC变换器建模与控制器设计
张纯江,赵 策,谢季芳,AHMAD Waseem,乔玉玺,阚志忠
(燕山大学河北省电力电子节能与传动控制重点实验室,河北秦皇岛066004)
0 引言
在储能系统中,双向DC/DC变换器作为储能单元和直流母线的接口,发挥着重要的作用[1-2]。储能单元对电流纹波比较敏感,若输入电流纹波较大,会在一定程度上影响储能单元的使用寿命[3]。同时,储能电池的电压等级通常低于直流母线,这就要求接口变换器具有一定的升压能力,另外,储能用隔离DC/DC变换器需要具有功率双向传输的功能。电流型双向DC/DC变换器由于输入侧电感的存在,可以在减小输入电流纹波的同时提高电压增益,在储能场合中应用很广[4-5]。常见的电流型DC/DC变换器包括不对称半桥变换器、有源箝位双Boost变换器、推挽式双向DC/DC变换器[6]等。本文将重点对推挽式双向DC/DC变换器展开研究。
值得注意的是,学者们关注的重点往往是变换器的工作原理和稳态特性,而对变换器的动态特性和闭环控制的研究比较少。在实际的储能系统中,无论是负载的扰动、储能单元端电压的变化,还是传输功率的正反向切换,都需要良好的闭环系统进行控制。因此,对变换器建立准确的小信号数学模型,并设计相关闭环控制器就显得尤为重要。
常见的电路建模方法包括状态空间平均法、扩展描述函数法和离散时间法等。状态空间平均法是最常见的电路建模方法,通过对不同模态的状态方程进行加权平均,得到系统整体的状态空间平均模型,在变换器稳态工作点引入扰动量并进行线性化处理,最终得到变换器的小信号数学模型。文献[7]采用状态空间平均法对交错并联磁集成三电平双向DC/DC变换器建立了数学模型,并设计了闭环控制器。
扩展描述函数法主要应用在谐振式电路建模中。由于谐振式电路中开关频率与谐振频率非常接近,开关频率的纹波不能进行忽略,状态空间平均法不再适用。扩展描述函数法的核心是将非线性环节在正弦信号下的输出,通过傅立叶分解只保留基波特性,从而得到线性环节的等效近似频率特性,完成线性化处理。文献[8]通过扩展描述函数法完成了对双向LLC谐振变换器的数学建模,并设计了控制环路反馈补偿器。
离散时间法是以变换器的工作模态为基础,在时间域内对不同工作模态的状态变量进行分析[9],并反复迭代,直接获得时间域内数学表达式的一种方法。文献[10-11]应用离散时间法对双有源桥电路做了相关研究,在考虑输出电容等效串联电阻(Equivalent Series Resistance,ESR)和数字延迟的基础上,建立了双线性离散时间模型,并分析了变压器漏感、输出电容ESR对控制参数稳定性边界的影响。
对于推挽式双向DC/DC变换器而言,传输电感电流一个开关周期内的平均值为零,无法用传统的状态空间平均法直接描述。扩展描述函数法主要解决谐振电路的建模问题,不适合本电路。而离散时间法中迭代次数随电路工作模态数量增加,过程比较复杂,并且不能直接指导控制器的设计,应用起来比较困难[12]。
本文在研究推挽式双向DC/DC变换器工作原理的基础上,提出一种模态平均分级建模方法,通过模态平均电流代替周期平均电流,解决了状态空间平均法无法直接描述传输电感电流状态变量的问题。同时,为了达到合理降阶,将原电路解耦为前、后两级,建立了低阶非耦合的小信号数学模型。由于变换器有箝位电容电压和输出电压两个变量需要控制,分别设计了以控制箝位电容电压为目标的电压电流双闭环控制器和以控制输出电压为目标的移相环控制器,从优化系统动静态性能出发对控制器参数进行了详细的分析和设计。对所建立的双闭环控制系统进行了仿真研究,获得了良好的静动态性能,验证了所设计控制器参数的合理性。
1 变换器拓扑及工作原理
1.1 拓扑结构
推挽式双向DC/DC变换器拓扑结构如图1所示。低压侧开关管S1、S2为主控管,S3、S4为有源箝位管,连接箝位电容Cs。升压电感L与低压侧变压器原边中心抽头直接相连,构成Boost升压电路,从而构成了推挽电路结构。中间隔离级采用推挽变压器,完成高压侧与低压侧的隔离,并通过传输电感Ls实现功率的传输。高压侧采用倍压整流电路,S5、S6为同步整流管,C1、C2为倍压电容,R为负载电阻。图中,V1为低压侧端口电压,V2为高压侧端口电压,vab为原边折算电压,vcd为副边折算电压。分析变换器的工作过程,可以对变换器实现如下拆分:①升压电感L、低压侧全桥电路、变压器T构成升压电路,输入电压V1经过升压后变为箝位电容电压VCs;②低压侧全桥电路、变压器T、传输电感Ls和高压侧倍压整流电路构成了类双有源桥电路,不同之处在于高压侧用半桥电路代替了全桥。箝位电容电压经过此电路实现功率传输。拆分后的等效原理图如图2所示,两个电路共用功率开关管S1-S4和变压器T。

图1 拓扑结构图Fig1 Topological structure diagram

图2 拆分后的等效原理图Fig.2 Equivalent schematic diagram after split
1.2 工作原理
低压侧S1和S2是主控管,占空比为D,并且驱动信号的相位差为π。S1和S3、S2和S4的驱动信号分别互补。高压侧S5和S6的占空比固定为0.5并且互补。推挽变压器匝数比为N1∶N2∶N3=1∶1∶n。定义S5驱动信号对于S1驱动信号的移相比为φ,移相比φ为移相角与2π的比值。在以下分析中,忽略各开关管之间的换流时间,且遵循以下假设:①变换器所有功率器件均为理想器件;②箝位电容Cs和倍压电容C1、C2无限大,电容电压纹波可以忽略不计;③推挽变压器为理想变压器;④忽略线路寄生参数的影响。
变换器采用PWM+移相控制实现原、副边电压的匹配即幅值相等,在实现功率传输的同时,可以减小系统的回流功率,其调制策略和关键波形如图3所示。通过控制主控管S1的占空比来控制箝位电容平均电压VCs,控制移相比φ来调节输出电压V2,进而控制系统的功率传输。

图3 变换器的关键波形Fig.3 Key waveform of the converter
根据升压电感L在一个开关周期内的伏秒平衡原理,可以得到箝位电容平均电压VCs和输入电压V1的关系如下:
(1)
此变换器中原、副边折算电压的幅值Vab和Vcd表达式如下:

(2)

(3)
变换器的调制策略中遵循了原、副边折算电压幅值相等的原则,所以由式(2)、式(3)可以得到输出电压V2和输入电压V1的静态关系如下:

(4)
变换器的功率传输关系为

(5)
2 数学模型
本电路中储能元件较多,若采用整体建模的方式,得到的数学模型阶次较高,不利于控制器设计。并且传输电感电流一个开关周期内平均值为零,无法用状态空间模型直接描述。对此,本文提出一种模态平均分级建模方法,通过将模态平均电流代替周期平均电流,将电感电流交流量用各模态直流量进行描述,并按照功率守恒、电压等级匹配的原则,根据图2将其等效为前、后两级电路,建立电路的数学模型。
2.1 前级建模
前级为Boost升压电路,建模时不考虑后级的影响,整个后级系统用等效电阻替代。根据功率守恒的原则,等效电阻R0的表达式为
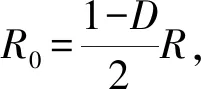
(6)
其他参量的取值保持不变。
前级等效电路如图4所示,共有4种工作模态,分别对应图4(a)~(d)。
1) 阶段1,3

(7)
2) 阶段2,4
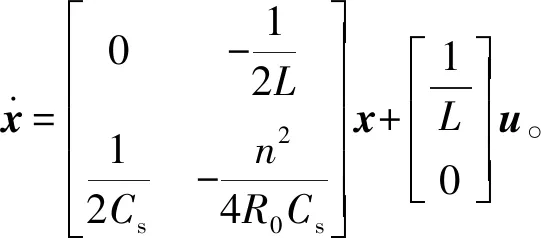
(8)
对上述表达式进行加权平均,得到等效状态方程:

(9)

(10)

图4 前级等效电路图Fig.4 Front stage equivalent circuit diagram
对小信号线性表达式做拉普拉斯变换并计算,可得升压电感电流与占空比、箝位电容电压的关系如下:

(11)

(12)
2.2 后级建模
后级为类双有源桥电路,建模时不考虑前级Boost升压电路的影响。将箝位电容Cs等效为电压源,后级等效电路如5所示,共有6种工作模态,分别对应图5的(a)~(f)。各工作模态的状态方程如下:

(13)
其中,vc12为倍压电容C1、C2的电压之和,C为倍压电容C1、C2的电容值。
需要注意的是,传输电感电流iLs一个开关周期内的平均值为零,不能直接用状态空间平均模型描述,而不同工作模态中,传输电感电流平均值不再为零。所以,本文提出一种模态平均的处理方法,用不同模态下电流平均值来替换开关周期平均值代入各模态状态方程中,传输电感电流模态平均值表达式如下:
式中,〈vc12〉Ts和〈vCs〉Ts为其在一个开关周期Ts中的平均值。
将式(14)代入式(13)并进行时间加权,得到等效状态方程为

(15)
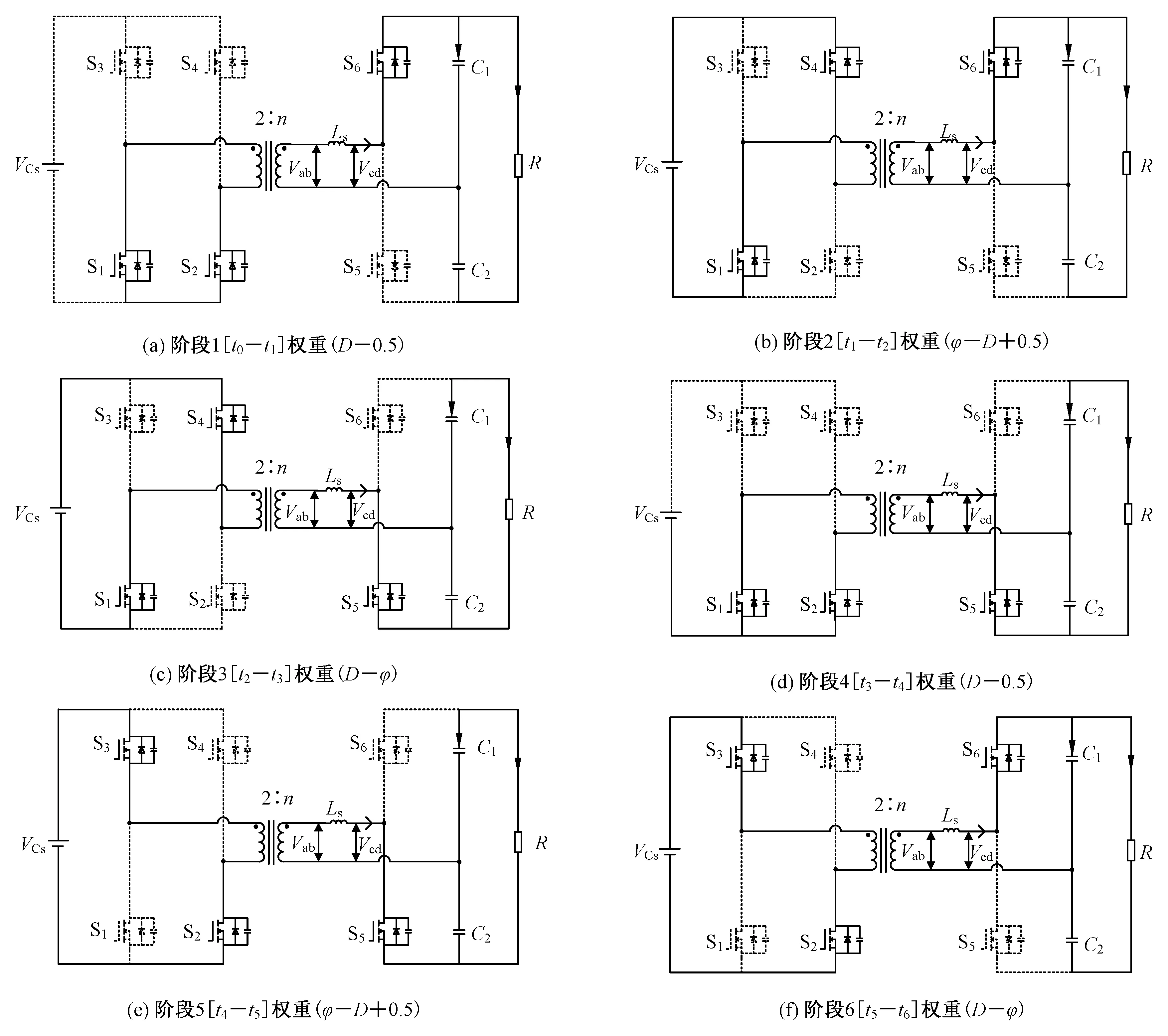
图5 后级等效电路图Fig.5 Backstage equivalent circuit diagram

(16)
对小信号线性表达式做拉普拉斯变换并计算,可得倍压电容电压之和vc12(即输出电压v2)与移相比φ的传递函数为

(17)
3 控制器设计
根据推挽式DC/DC变换器的工作原理,原电路进行了如图2所示的等效拆分,针对拆分后的电路提出如下闭环控制策略:以控制箝位电容电压为目标的电压电流双闭环控制和以控制输出电压为目标的移相环控制。箝位电容电压vCs和输入电感电流iL与参考值比较后,经过电压、电流双闭环调节生成占空比D控制原边开关管。输出电压v2与参考值进行比较后,经过移相调节器生成移相比,以S1驱动信号的相位为基准对S5驱动信号进行移相,控制副边开关管。闭环控制示意图如图6所示。

图6 控制示意图Fig.6 Control diagram
参数设置:输入电压V1=96 V,输出电压V2=700 V,传输功率P=3 kW,升压电感取200 μH,传输电感取40 μH,箝位电容、倍压电容均为220 μF,推挽变压器匝比为1∶1∶3,开关频率为50 kHz。
3.1 前级控制器
前级Boost升压电路采用电压电流双闭环控制,控制框图如图7所示。其中Gv(s)为电压PI控制器,其表达式为Gv(s)=Kvp+Kvi/s;Gi(s)为电流PI控制器,其表达式为Gi(s)=Kip+Kii/s;Fm(s)为调制环节的传递函数,α、β为电压、电流环的反馈系数。这里取Fm(s)=1,α=1,β=1。

图7 前级电路的双闭环控制框图Fig.7 Block diagram of double closed-loop control of pre-stage circuit
校正前电流内环的开环传递函数为
Gio(s)=Gid(s)·Fm(s)·β
,
(18)
代入具体数值得校正前电流环的开环传递函数为

(19)
根据计算结果绘制伯德图,如图8所示。校正前剪切频率高于100 kHz,低频段幅频特性曲线斜率为0,这都不利于系统保持稳定。采用PI控制器对其进行校正后,低频段幅频特性曲线斜率变为-20 dB/(°),剪切频率为2 920 Hz,相角裕度74.8°,稳定性良好。电流PI控制器比例系数Kip=0.015,积分系数Kii=75。
校正后的电流闭环传递函数为

(20)
代入具体数值得电流内环的闭环传递函数为
Hid(s)=

(21)

图8 电流环伯德图Fig.8 Bode diagram of current loop
在进行双闭环设计时,电流内环的带宽要远远大于电压外环的带宽,为了简化计算,可以将电流内环的闭环传递函数等效为一阶惯性环节,做如下降阶处理:

(22)
校正前电压外环的开环传递函数为
Gvo(s)=Hid(s)·Gvi(s)·α,
(23)
代入具体数值得校正前电压环的开环传递函数为

(24)
电压外环同样采用PI控制器进行校正,校正前低频段幅频特性斜率近乎于0,系统稳态精度不高。校正后低频段幅频特性曲线斜率变为-20 dB/(°),剪切频率为623 Hz,相角裕度66.8°,稳定性良好。校正前后的电压环伯德图如图9所示。电压PI控制器比例系数Kvp=2.09,积分系数Kvi=2 090。
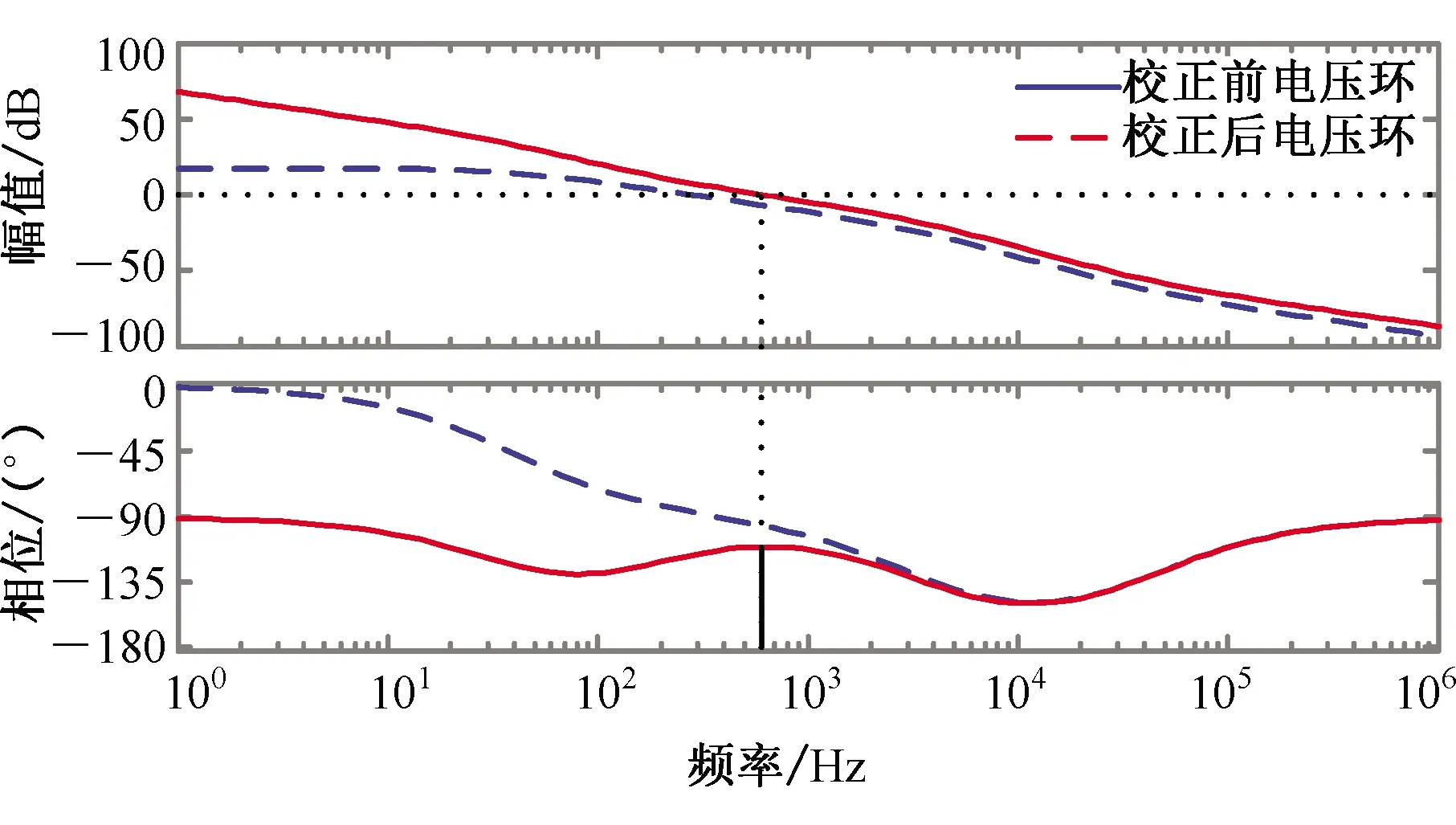
图9 电压环伯德图Fig.9 Bode diagram of voltage loop
3.2 后级控制器
后级类双有源桥电路为一阶系统,采用单移相环进行控制,控制框图如图10所示。其中Gφ(s)为移相PI控制器,其表达式为Gφ(s)=Kφp+Kφi/s;Fm(s)为调制环节的传递函数,γ为移相环的反馈系数。这里取Fm(s)=1,γ=1。

图10 后级电路的移相环控制框图Fig.10 Block diagram of the phase-shift loop control of the post-stage circuit
校正前移相环的开环传递函数为
Gv2o(s)=Gvφ(s)·Fm(s)·γ,
(25)
代入具体数值得校正前移相环的开环传递函数为

(26)
移相环采用PI控制器进行校正,并绘制伯德图如图11所示。校正前剪切频率接近100 kHz,低频段幅频特性曲线斜率为0,不利于系统稳定。采用PI控制器对其进行校正后,低频段幅频特性曲线斜率变为-20 dB/(°),剪切频率为3 010 Hz,相角裕度48.7°,稳定性良好。移相PI控制器比例系数Kφp=0.023 3,积分系数Kφi=388.33。

图11 移相环伯德图Fig.11 Bode diagram of phase shift loop
4 仿真验证
仿真参数与上述设计参数一致,图12为升压电感电流iL和推挽变压器绕组电流in1、in2的波形图。推挽变压器原边两个绕组工作方式是对称的,实现了电流均分。升压电感电流纹波为1 A,脉动频率为开关频率的2倍。

图12 电感电流和推挽变压器电流波形Fig.12 Inductor current and push-pull transformer current waveforms
图13是折算后的原边电压vab、副边电压vcd和传输电感电流iLs的波形图。通过PWM+移相控制,系统实现了原、副边电压匹配,vab、vcd的幅值均为输出电压的一半即350 V,在电压匹配时间内iLs保持不变,可以减小传输电感电流的峰值,降低电流应力。

图13 原、副边折算电压和传输电感电流Fig.13 Converted primary and secondary voltages and transmitted inductor current
图14为系统负载突加减的闭环仿真波形。在0.05 s时,负载功率由3 kW突变为1 kW,输入电感电流由31.25 A变为10.42 A,输出电压v2、箝位电容电压vCs在3 ms内完成跟踪,波动在10 V以内。在0.075 s,负载功率由1 kW突变为3 kW,输入电感电流由10.42 A变为31.25 A,输出电压v2、箝位电容电压vCs在3 ms内完成跟踪,跌落在10 V以内。系统具有良好的跟随性和稳定性。
图15为系统正反向切换运行的闭环仿真波形。在0.1 s时,传输功率由正向3 kW变为反向3 kW,系统在4 ms内实现了平滑切换,输入电流iL由+31.25 A变为-31.25 A。输出电压v2、箝位电容电压vCs波动均在合理范围内。在0.15 s,传输功率由反向3 kW变为正向3 kW,系统在4 ms内实现了平滑切换,输入电流由-31.25 A变为+31.25 A。输出电压v2、箝位电容电压vCs波动均在合理范围内,系统具有良好的跟随性和稳定性。

图14 负载突加减仿真波形Fig.14 Load sudden addition and subtraction simulation waveform
5 结论
本文提出了一种新型的模态平均分级建模方法,该方法解决了传输电感电流一个开关周期平均值为零,无法直接用状态空间平均模型描述的问题,并将电路解耦成两级并分别进行建模,得到了推挽式DC/DC变换器的低阶非耦合小信号数学模型。根据所得小信号模型,设计了以控制箝位电容电压为目标的前级电路的电压电流双闭环控制器和以控制输出电压为目标的后级电路的单移相环控制器,从系统的稳定性和动静态性能角度对控制器参数进行了设计,通过负载突加减、变输入电压、正反向切换运行等仿真验证了小信号模型的准确性和控制器的有效性。

图15 正、反向切换运行仿真波形Fig.15 Forward and reverse switching simulation waveform

