理论力学教学中的土力学算例设计与实践

卢玉林，陈晓冉，林 玮

(1.防灾科技学院 土木工程学院，北京 101601；2.防灾科技学院 地质工程学院，北京 101601)

0 引言

理论力学是土木类专业的一门重要基础课，是从抽象力学到实用力学转变的伊始，更是专业知识和专业素养提升的重要基石[1]。如何更好地突出理论力学在专业人才培养中的作用，是当前力学教师思考的热点问题之一。

在“双创”教育背景下，理论力学面临学时压缩的严峻挑战，更有部分学生和专业课教师对理论力学在专业人才培养中的作用认识不深，加剧了基础力学课程与专业课程学时分配的矛盾。根据多年的基础力学教学经验，分析和总结了产生这一矛盾的主要原因有：(1)理论力学的授课教师专业多以力学背景为主，或理论力学课程归属在各高校的理学院或基础部，教师在讲授过程中偏向基础理论讲解，而缺乏必要的专业工程背景介绍和应用；(2)理论力学教材中的案例设置偏向机械、航空类专业，运动学和动力学部分的例题和习题多以传动机构为主，与土木、交通类专业中以“静”为主的工程案例截然不同，抑制了理论力学的学习动力；(3)理论力学教学中的力学思维模式和解析方法的思想未能建立，造成了专业课中涉及计算的问题，还要回顾和重复已学的知识，降低了理论力学的核心作用[1-4]。

如何保持理论力学的青春活力，在讲授过程中引入一定的工程案例是值得提倡的。选取案例必须慎重，既要保证理论力学和专业课程的契合度，又要减轻专业课程中力学计算的负担。笔者授课的对象有土木工程、城市地下空间工程和地质工程等专业，而土力学是3个专业后续共有的基础课，在理论力学教学中引入土力学算例，直面算例的工程性，可丰富理论力学的吸引力和创造力[5-8]。通过连续2年的跟踪调查，实践表明这一教学设计在教学效果中发挥了重要的积极作用，缓解了土力学授课教师讲授工程案例计算的压力，提高了理论力学在学生中的地位，助力了土木类专业的人才培养。

1 土力学算例设计

1.1 一道例题引发的思考

哈尔滨工业大学理论力学教研室编写的《理论力学》第8版中例2-6描述了平面力系的简化问题，如图1所示[1]。由此例题思考了这样一个问题，例题中的F1=300 kN和F2=70 kN是一个集中力，显然F1和F2描述的应该是重力坝两侧静水压力的合力，用合力代替分布力是该题的简化措施，目的是使学生易懂，遗憾的是静水压力通常以分布力来表示，这与土力学中给出工程算例不符。

值得注意的是F1距坝底的高度是3 m，恰作用在蓄水高度的1/3处，这与静水压力的合力所在位置是重合的。然而，如果按照合力计算公式得到F1=0.5ρgh2=0.5×1000×9.8×92=396.9 kN，这与例题给出的已知量又不符，出现了矛盾。如何解释这一矛盾？是因为例题并未完全考量自身的工程性。

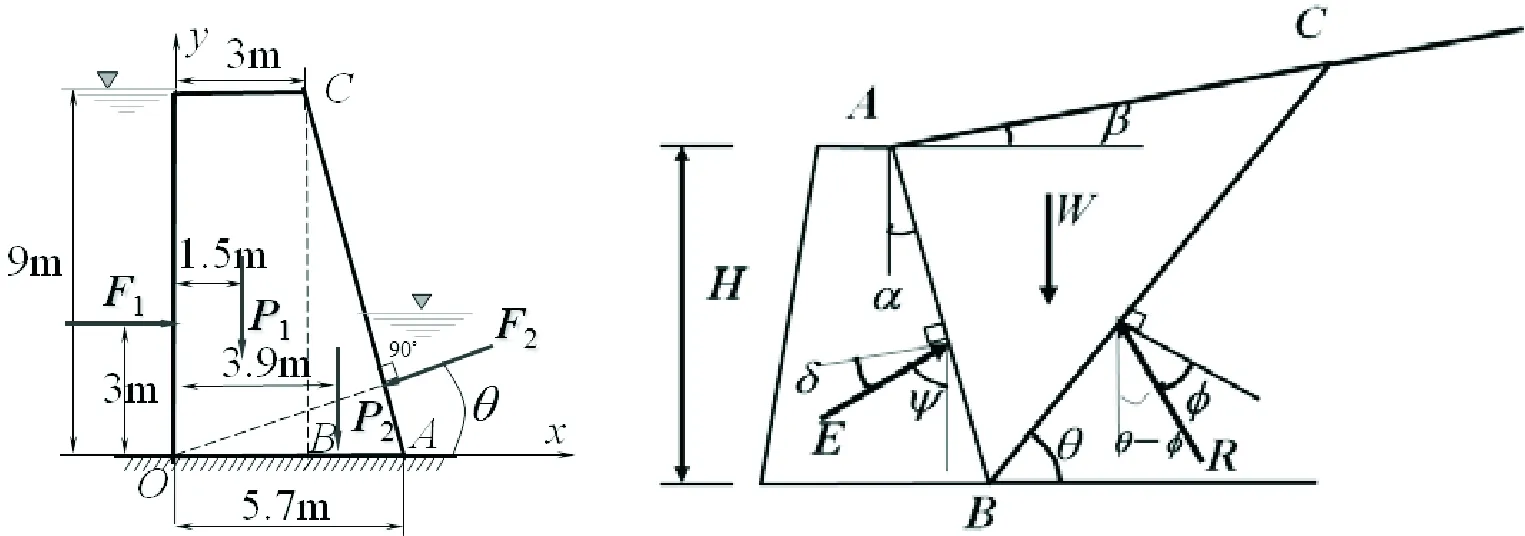
图1 例题2-6示意图 图2 库伦土压力计算模型示意图

基于例题的工程性和与后续课程衔接性的考量，在理论力学教学中，根据授课内容设计和引入土力学相关算例，用理论力学的思维方法思考、分析和求解，用以建立统一的课程闭环。以下分别从静力学、运动学和动力学三部分列举土力学中的例题设计。

1.2 静力学中的算例设计举例

土压力是土力学中的主要计算内容之一，分为静止土压力、主动土压力和被动土压力。法国科学家库伦(Coulomb)于1773年提出了主动土压力和被动土压力的概念和计算方法，他在滑动土体上建立力系的平衡条件求解土压力，见图2所示[5]。可以看出，图2与例题2-6的本质是一样的，都是平面力系下的简化和平衡问题，求解思路完全一致，只需交代一下相关计算参数就可实现求解，但该算例已成功过渡到了土力学问题，对土木类专业而言是非常有吸引力的。

朗肯土压力是英国科学家朗肯(Rankine)于1857年根据半无限空间体的应力状态和土体单元的极限平衡所得出的，本部分内容在引入时并不涉及应力状态的概念，而是从应力分布函数讲起，并结合合力矩定理和平面力系的简化来分析、求解。

朗肯土压力分布和例题2-6中的静水压力分布有着密切的联系，都是压力随深度的增加而线性增加，因此距地面任意位置处的土压力可用土体的重度与深度之积表示，再根据压力类型乘以相关系数即可得到相应的土压力值。这一点在授课中主要强调压力的计算方法，对压力系数的由来以及推导过程不做重点介绍。对于无黏性土，由于黏聚力为零，无黏性土的三种土压力分布都是表现为随深度的三角形函数，即土压力的合力位于深度的1/3处，见图3所示[5]。如果将土压力向挡土墙底部简化，还可以可得到挡土墙的倾覆力矩，为挡土墙的安全性评价提供基础。

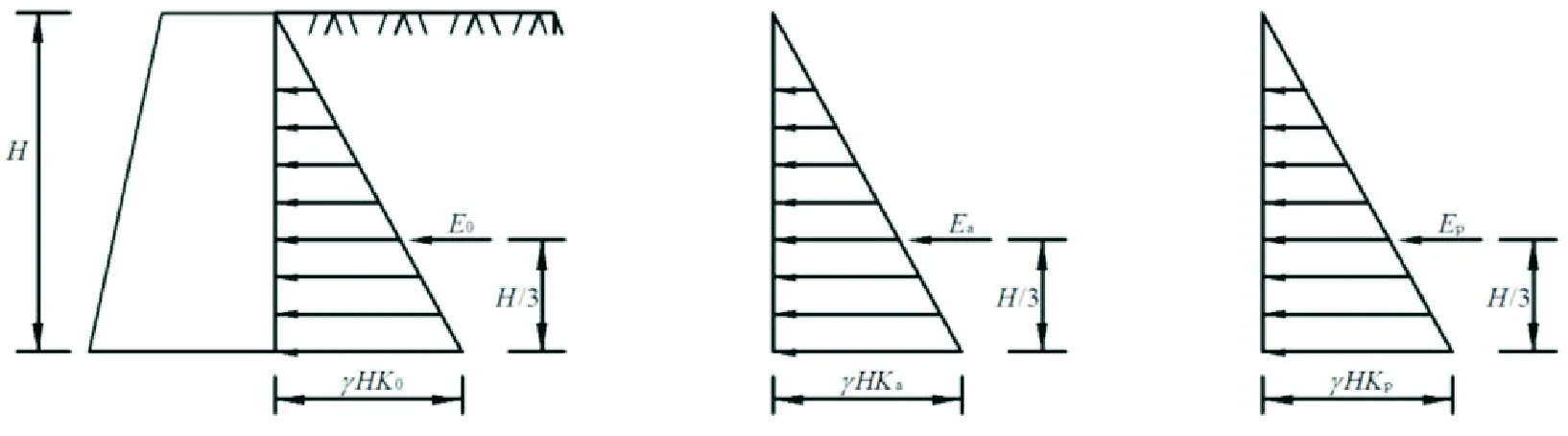
(a)静止土压力分布 (b)主动土压力分布； (c)被动土压力分布

对于黏性土，土压力分布见图4所示，其主动土压力和被动土压力分布并不相同，主动土压力的计算仍可以简化为三角形荷载问题处理，但被动土压力需简化为梯形荷载处理。由平面力系的合力矩定理即可计算出相应的土压力合力以及所在位置，运用的分析方法仍然是平面力系的基本知识，但例题已具有了较强的实用性[5]。

(a)主动土压力分布； (b)被动土压力分布

在静力学部分，理论力学教材上还有很多涉及梁的问题，与土木工程专业联系密切，也是授课过程中重点要讲授的算例，此处不再赘述。

值得注意的是土力学中重要的砂土强度理论表示为τf=σtanφ，即抗剪强度与破坏面上法向应力之比为内摩擦角的正切值，该公式与理论力学中的库伦摩擦定律非常相似。

1.3 运动学中的算例设计举例

运动学是理论力学中贯穿静力学与动力学的基础，这部分中点的合成运动和刚体的平面运动是学生早前未接触的新知识点，教材中列举的大部分例题是围绕机械运动展开的，如何将这部分知识点化解为土力学的算例是个难点。

防灾科技学院是以防灾减灾教育为主的特色院校，《自然灾害》是本科生的一门通识课，讲授内容包括地震、海啸、滑坡、泥石流等常见的自然灾害知识。以下举例用合成运动分析土力学中边坡受振动运动的案例，如图5所示。边坡受振动后出现滑坡灾害，运动的滑体与山体之间产生了相对运动，而滑体与远处不动山体构成了绝对运动，振动的山体与静止的大地构成了牵连运动，由此可以从滑坡运动中解释点的合成运动中的三个基本概念。点的合成运动的关键是动点的选取，然而在土力学中针对某一点的研究非常罕见。土力学以平面滑体为研究对象，而举例中的滑坡运动分析似乎与点的合成运动在概念上又是不统一的。如果把滑坡的运动分析进一步精化为力学模型，实质上滑坡运动就是点的合成运动的具体化。

圆弧法是边坡稳定分析的基本方法之一，是瑞典教授彼得森(Petterson)在1916年提出的条分法的改进形式，它的基本思想是将边坡失稳简化为绕某一圆心的滑动。基于上述理论，滑体自身是刚体，则滑体可看作一质点系，精细化为质点；滑动面的位置是固定的，不随时间和振动的强弱发生改变，则滑动面可等效一圆弧状的滑槽。经过简化，滑坡的运动力学模型是符合点的合成运动的，简化模型如图6所示。

图5 边坡滑体滑动示意图 图6 点合成运动下的边坡滑动简化图

以上讲解时要特别注意简化的思想以及铰支座与滑体之间二力杆的由来，重点是理解运动学中的基本概念，以此来扩展分析思路，为合成运动的求解提供基础。

1.4 动力学中的算例设计举例

动量矩定理是动力学中的重要定理之一，质点系的动量矩定理可描述为：质点系对于任意点的动量矩对时间的导数，等于作用于质点系的外力对同一点矩的矢量和，对平面内取固定点或固定轴，则可以用投影式来表示，即

(1)

以下举例说明利用动量矩定理的投影式来求解土力学中边坡失稳的运动学参数。土力学中瑞典圆弧法计算的核心是滑体绕某一空间位置产生整体滑动，滑动面犹如一圆柱面，如图7所示。为了方便计算，可将三维滑动投影至平面得到滑坡整体失稳的平面计算模型，如图8所示。

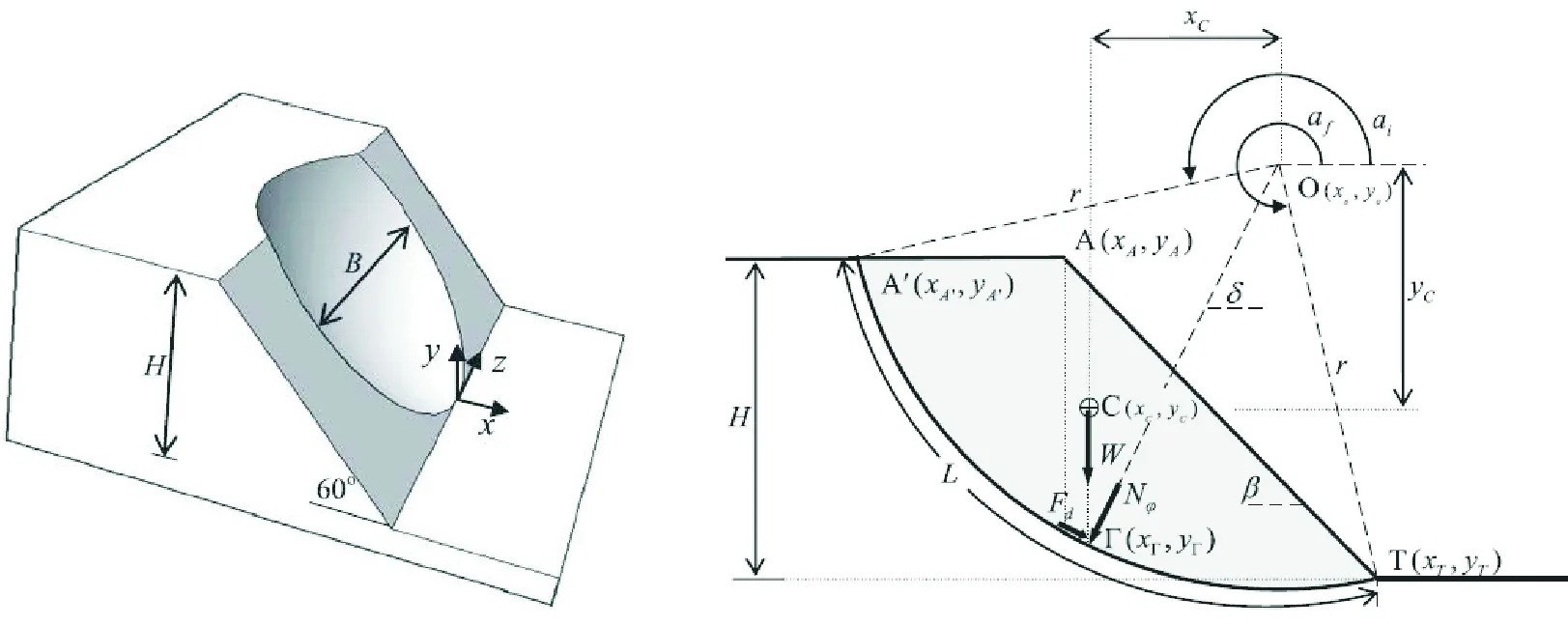
图7 边坡整体失稳示意图[9] 图8 边坡失稳计算示意图[10]

通过滑体运动学分析可知，滑体在滑动过程中表现为平面运动，如9所示。基于刚体平面运动的瞬心法，通过滑体不同位置的速度可以确定出滑体的矩心就是滑体的速度瞬心，且滑体质心与速度瞬心的距离保持不变，由此可以推断出滑体相对于速度瞬心的动量矩对时间的导数，就等于作用在滑体的外力系对速度瞬心的主矩。而土力学中瑞典圆弧法计算的力矩与动量矩定理等式右端出现的力矩表达式是一致的，边坡稳定性系数可通过滑动面上抗滑力矩与下滑力矩之比来表示，即

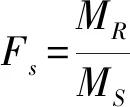
(2)

取滑体为研究对象，滑体上所有外力对O点之矩，就归类为下滑力矩和抗滑力矩，而二者的合即为动量矩定理等式右端的力矩项。通过上述分析，在瑞典圆弧法中应用动量矩定理就可以确定滑体在下滑时滑动面上的角加速度。角加速度确定后，再建立滑体整体临界条件下的加速度，这对分析失稳具有重要参考价值。

此外，该例题计算过程中还要涉及滑体的质心位置、转动惯量、平行移轴公式等知识点，是一道综合性强的算例。

以上举例可以说明，在理论力学教学中可以有效地穿插土力学算例，从静力学、运动学到动力学，设计有关算例对理解理论力学的基本概念和核心公式有极大地启发作用。另外，在讲解案例时，可结合理论公式的历史背景展开，点题深思、扩展广度和深度，为继续深入学习和掌握土力学的相关理论提供帮助[11]。

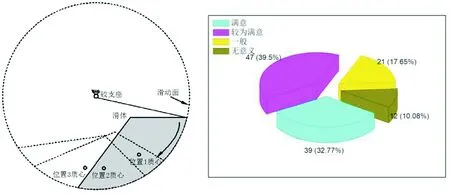
图9 滑体滑动示意图 图10 结果总体分布

2 教学效果调查与反思

理论力学开设学期为大一春季，土力学开设学期为大三秋季，连续跟踪了2015级和2016级土木工程专业2个教学班和2016级城市地下空间专业1个教学班的学习情况，在土力学的教学中通过匿名问卷调查了两门课程的衔接度和满意度，最终将调查结果概化为四级，即满意、较为满意、一般和无意义，如表1所示。

表1 跟踪班级调查结果

通过表1可以看出，引入案例的教学设计总体效果令人满意，大多数学生认为理论力学中的一些算例对土力学的学习有积极的作用，能够较为熟练地对算例进行受力分析和计算，虽然初次计算结果不理想，但能自主利用已学知识完成纠错。

3个班级的整体调查结果分布如图10所示，较为满意的学生人数最多为39%，认为一般和无意义的学生总占比为33%，即2/3的学生都认可此类教学设计，对学习有一定的积极作用。图10也反映出一定数量的学生对教学设计并不积极，通过调查发现主要问题在于以下3点：(1)两门课程的时间跨度大，已学的知识点基础不牢，无法形成知识链；(2)运动学和动力学部分的基本概念模糊不清，理解有偏差；(3)教学算例与授课形式单调，缺乏生动性链接。

上述提出的3点问题是值得反思的，也为今后的教学设计提供了改进建议。首要解决的问题是强化理论力学中的基本概念和基本公式的讲解，要夯实知识点。另外，在算例选取上还需经过严格的论证，要不断与土力学教师研讨，借鉴思路。

3 结束语

在理论力学教学中设计和引入土力学相关算例是教学内容的一个尝试，目的是让学生了解理论力学对后续专业课程的作用，同时也对专业培养方案中不同的课程形成了闭环。实践表明，大多数学生认可此类教学设计，但也存在不同观点，这就对授课教师提出了更高的要求，需要教师不断地改进教学设计和丰富案例，抓住课程之间的共性点，多举措提高基础力学的教学效果[12]。