UHPC纤维定向法及对受拉性能影响
张 阳,屈少钦,卢九章,霍文斌
(1.湖南大学 风工程与桥梁工程湖南省重点实验室,湖南 长沙 410082;2.北京市政路桥管理养护集团,北京 100097;3.广东省建筑设计院有限公司,广东 广州 510010)
0 引 言
超高性能混凝土(UHPC)是一种抗压强度超过150MPa的新型纤维增强水泥基复合材料[1],原材料组成为石英砂、活性掺合料、惰性掺合料、纤维、高效减水剂、水等。UHPC基于最大堆积密度理论和纤维增强理论开发,内部分散的短切纤维能有效抑制裂缝的形成和发展,提高UHPC的抗拉性能。
通常UHPC内纤维取向呈现乱向分布,如果让纤维取向倾斜于受拉方向,其抗拉强度、韧性和阻裂性能会大幅提升[2]。现有研究表明,UHPC内纤维取向倾向于浇筑UHPC时,新拌UHPC流动的方向[3]。部分学者[4-6]根据这一特性,通过特殊的浇筑手段,让新拌UHPC在模具中流动,实现纤维定向的效果。另外钢纤维作为一种导磁性介质,慕儒[2]等采用电磁场作用实现了UHPC的纤维定向,相较于流动浇筑法,UHPC的受拉性能提升更大。同时,纤维定向会导致UHPC在纤维取向以外的力学性能降低[7],因此,在双向受力板、复合受力构件(牛腿、刚节点等)以及其他复杂受力结构中,应尽量避免采用定向纤维UHPC,但如果将其用于轴向受力构件(如桁架受拉杆)时则具有明显的优势。
确立UHPC受拉性能与纤维取向之间的关系是开发应用定向纤维UHPC的关键之一。研究人员试图量化纤维取向的参数与UHPC受拉性能之间的联系,参数如表1。B.BOULEKBACHE[3]、L.FERRARA 等[7]提出的纤维取向系数θ被广泛作为评价纤维取向程度的指标,他们发现UHPC的受拉性能随着纤维取向系数的增加而提高;F.GERMANO[8]提出的取向数η和S.T.KANG[4]等提出的纤维取向因子ηφ也得到了较为广泛的认可,这两个指标与UHPC的受拉性能表现同样正相关;G.TIBERTI[9]综合了相关纤维取向指标,提出了更加合理的纤维增强效率比ρf,eff,并发现UHPC的断裂能与该指标存在线性关系。试验表明,上述指标均与UHPC受拉性能存在某种联系,但是尚无确切的计算公式将UHPC的抗拉强度与纤维取向指标联系起来。H.H.HUANG[10]等根据试验结果拟合得到近似的线性回归方程,但其普遍适用性还有待进一步验证。

表1 纤维取向评估方法
基于研究现状,笔者提出了一种用于UHPC纤维定向浇筑的方法,并采用图像分析技术[4,11]和UHPC轴拉试验,重点分析纤维定向浇筑对UHPC内纤维取向分布的影响,以及纤维取向分布与UHPC抗拉强度之间的定量关系。
1 定向浇筑
试验选择体积掺量3%的钢纤维增强UHPC,由于较高纤维掺量会导致UHPC工作性和流动性降低,直接让UHPC在模具中流动会变得十分困难。笔者设计了一套浇筑装置,用于UHPC的纤维定向浇筑,如图1。

图1 UHPC纤维定向浇筑装置
定向装置主要由定向通道、振动台及可移动的模具组成。定向通道的作用是让新拌UHPC在进入模具前产生一个流动的过程,从而改变新拌UHPC内纤维的取向分布;振动台的作用是克服由于UHPC工作性差引起的浇筑问题,当振动台未启动时,倒入斜置的定向槽的新拌UHPC难以流动,启动振动台并将定向槽斜置在振动台上,新拌UHPC能够快速沿着定向槽流下,保证了UHPC纤维定向的可实施性。
UHPC纤维定向浇筑的具体流程大致如下:首先,启动振动台,将定向通道斜置在振动台上,倒入新拌UHPC至定向通道上方,UHPC在振动作用下快速下流;然后,持续移动模具并保证足够的移动速率,以提供一个额外的拖拽作用,并迅速铺满一层;重复上述过程,通过定向浇筑多层以填满模具内部。
纤维定向浇筑中有两个方面改变UHPC内纤维的取向分布。一方面新拌UHPC在定向通道中流动的速度梯度[3],这一作用发生在图1中AB点之间。通道边壁的限制使得UHPC在通道流速随着与边壁的距离的增大而增加,从而形成速度梯度,原理如图2;当纤维方向与流动方向存在一定夹角时,速度梯度就会带动纤维向流动方向旋转。

图2 纤维在新拌UHPC流速场中旋转
另一方面新拌UHPC从定向通道流入模具过程中受到的拖拽作用,主要发生在图1中C点处。在纤维定向浇筑过程中,为了让流入模具中的UHPC能够顺着UHPC流动方向铺筑,应让定向通道不断与模具之间发生相对移动,当相对移动速度大于新拌UHPC的流动速度时,新拌UHPC在C点处由于速度差,产生较大的塑性变形,导致新拌UHPC沿受拉方向的长度增大,垂直流动方向的长度减小。这种塑性变形导致新拌UHPC内的钢纤维倾角进一步减小。
2 试验概述
试验所用UHPC原料配合比如表2,按不同浇筑方式设计了两组试件,其中一组试件(记为A-UHPC)采用1节所述纤维定向法浇筑,振动台频率为50 Hz,纤维定向通道由1 mm厚304不锈钢制成,几何尺寸如图3,其中18 mm指单个通道的内宽,其余尺寸均为外部尺寸。按照纤维定向方式浇筑试件,实测新拌UHPC需要6~8 s通过完整的纤维定向通道,平均流速为0.063~0.083 m/s,填满100 mm厚的试件需14~17层,共耗时42~68 s。另一组试件(记为R-UHPC,原料相同)采用普通的浇筑方式浇筑,普通浇筑时,新拌UHPC直接从模具中间位置倒入。浇筑完成后,所有试件均覆膜在室内养护48 h后拆模,拆模后的试件继续在室内(温度20~30 ℃、浇水后湿度80%左右)覆膜浇水养护至28 d龄期。
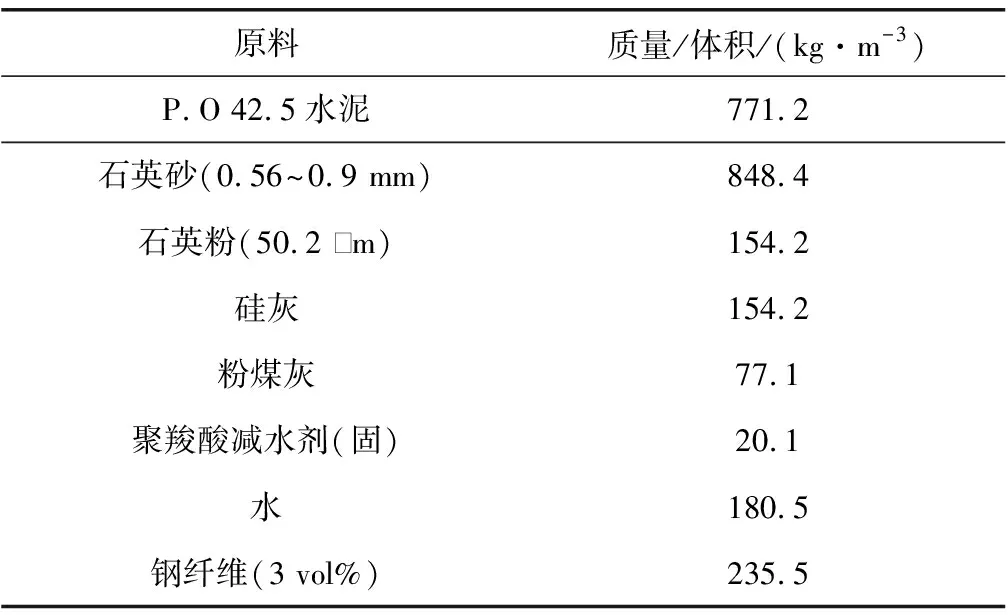
表2 UHPC原料配合比
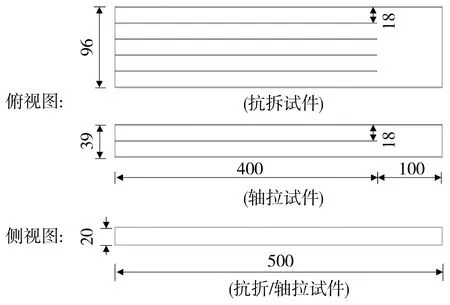
图3 纤维定向通道几何尺寸
每组试件分别包含3个抗折试件和3个轴拉试件,抗折试件尺寸(100 mm×100 mm×400 mm)和加载制度参照法国推荐标准NF P18-470[12]附录D中的切口试件四点抗弯试验,加载的装置如图4(a)。加载时试件跨径为300 mm,两个对称加载点间距100 mm,跨中设置有千分表测量抗折试件的跨中挠度,加载速率为0.15 mm/min。轴拉试件的尺寸和加载装置如图4(b),测量段横截面积为50 mm×100 mm,测量长度为150 mm,试件两侧分别固定有位移计测量UHPC的整体延伸量,加载速率为0.015 mm/min。
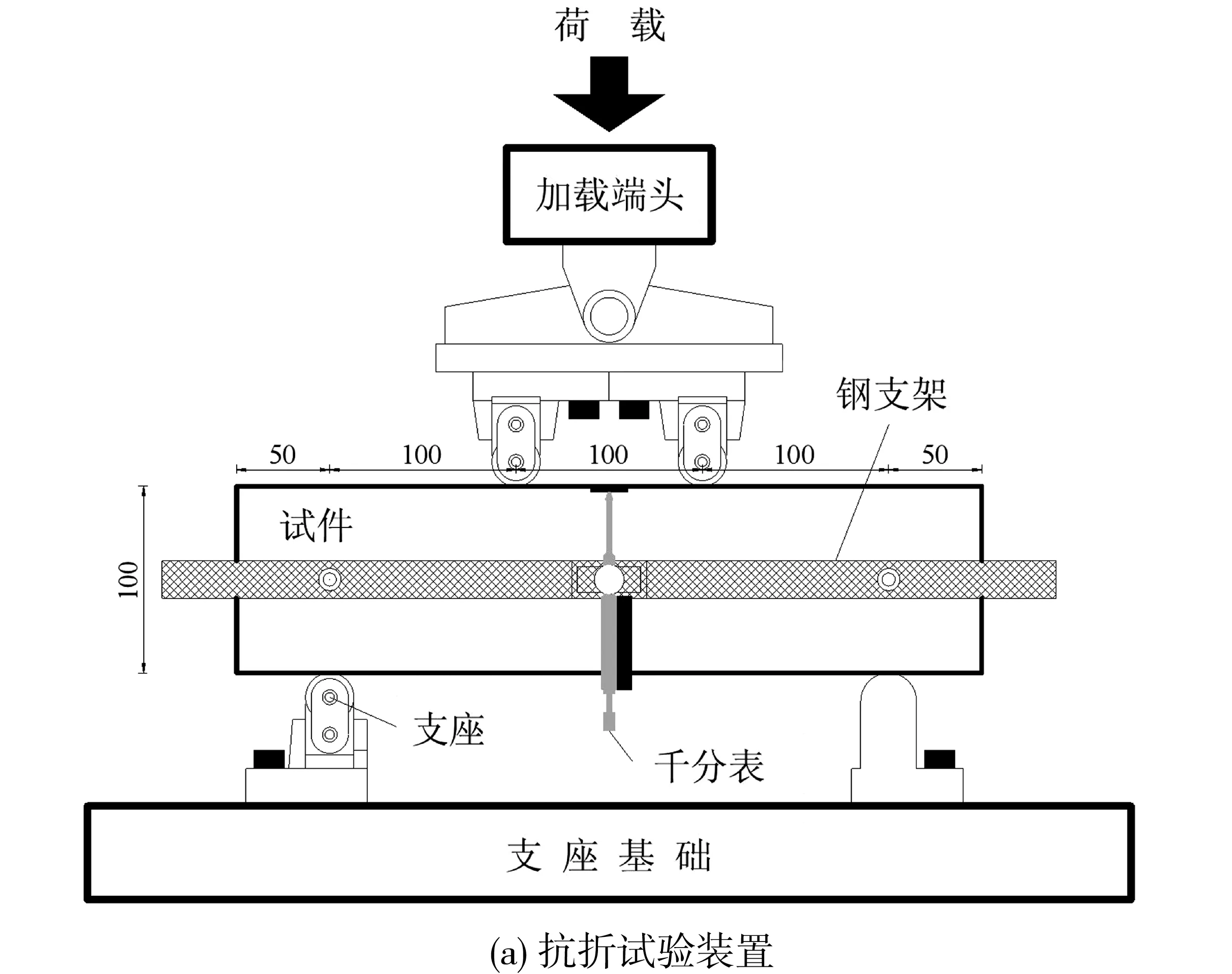
图4 试验试件尺寸及加载装置
3 UHPC纤维取向评估方法
3.1 图像处理
图像处理、透射X射线、CT成像,以及AC-IS都被用于分析UHPC中钢纤维的分布与取向[14]。其中,图像处理技术被认为是测试纤维分布与取向最实用、简便的方法。图像处理[12]通过对试件切片并拍照,获取切面图像信息,然后采用计算机对图像信息做二值化处理,提取UHPC切面上纤维的截面形状,计算纤维的倾斜角度,最终获得整个截面上的纤维取向分布。图像处理对原始图像清晰度要求较高,实际计算精度依赖计算机算法的合理性,通常计算结果与实际纤维取向存在一定差异,但不影响纤维的整体取向分布形式。
抗折试件或轴拉试件受拉破坏后,垂直于受拉方向切开未破坏的横截面并拍照,得到横切面原始图像如图5。由图5可知,R-UHPC的横切面纤维分布较稀疏,纤维切面形状较扁平,多呈扁平椭圆状,说明大部分纤维倾角偏大;A-UHPC横切面纤维分布较R-UHPC而言更加密集,纤维数量明显增多,纤维切面形状更接近圆形,大部分纤维倾角偏小。还可以看到,A-UHPC纤维分布有较为明显的层次感,这是因为分层定向浇筑,一定程度上会影响UHPC的整体性。

图5 UHPC切面纤维分布原始图像
通过计算机图像处理技术[4,11],可以得到横切面上所有钢纤维与截面法线夹角(即纤维倾角),统计得到过横切面纤维倾角分布频率直方图如图6。值得注意,通过某个横切面整合得到的纤维取向分布,只反映通过该横切面的纤维取向分布,但与UHPC内整体纤维的取向分布有一定的函数关系,故需要对数据进一步分析。
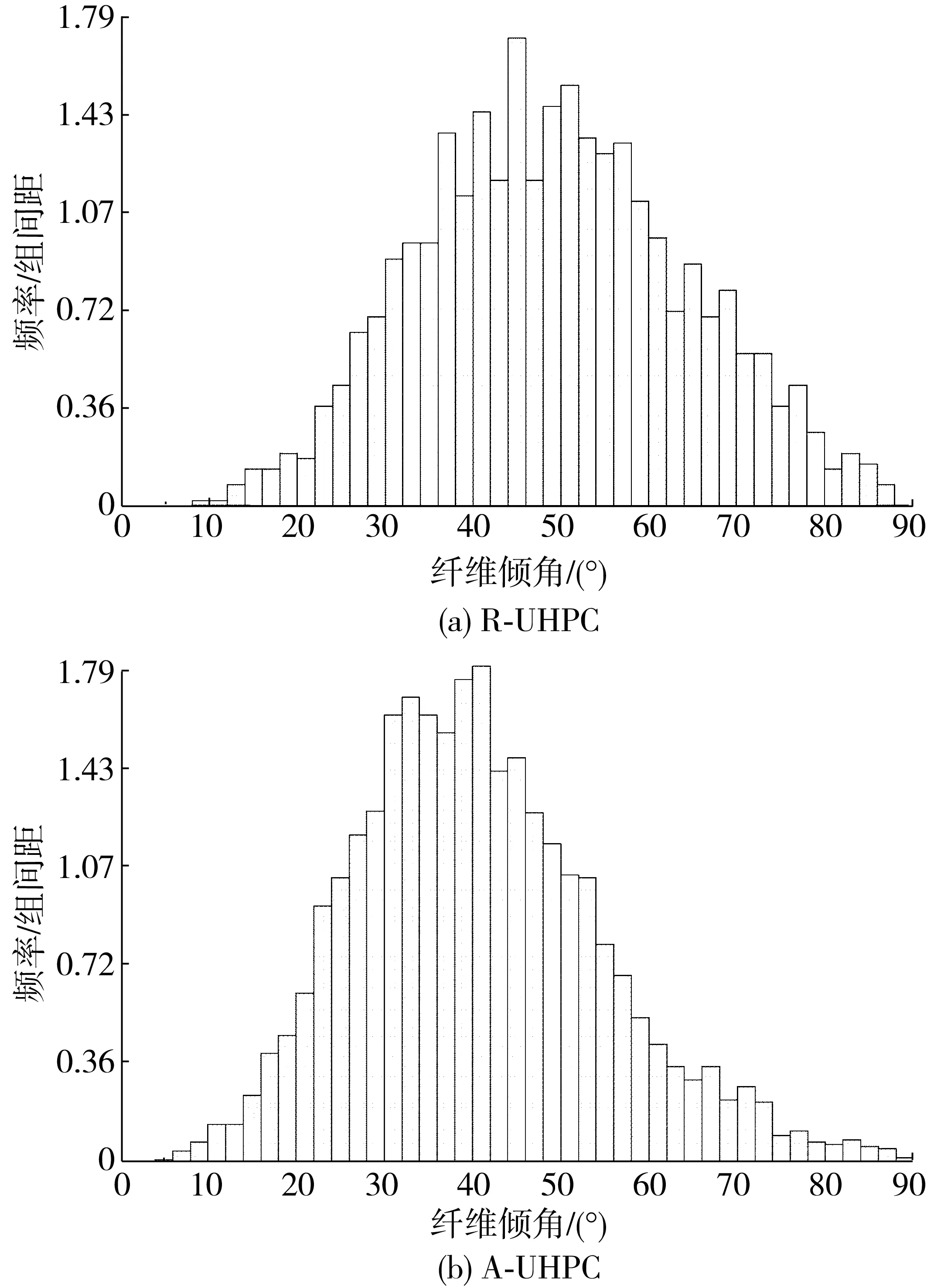
图6 切面纤维倾角频率分布直方图
给定任意横切面,纤维与横切面的空间位置关系如图7,其中lf为钢纤维长度,φ为钢纤维倾角。纤维与横切面的空间位置关系可分为3种:①实际过横切面的钢纤维,即图像分析的横切面上包含的钢纤维;②未过横切面的钢纤维,但是如果让它沿形心旋转一定角度,有可能穿过横切面,这种钢纤维的形心位置距离横切面不大于lf/2;③即使绕形心旋转一定角度也不能过横切面的钢纤维,这种钢纤维的形心位置距离横切面大于lf/2。

图7 纤维与切面空间关系
将UHPC内部空间用间隔lf的平行平面切割为若干空间,假设钢纤维形心在UHPC内部空间随机均匀分布,那么每一份空间中钢纤维都可以代表UHPC内部整体的钢纤维。取其中某个空间Ω,并设定空间中部的平面为切面,则上述前2种钢纤维为空间Ω内包含的所有钢纤维,其取向分布可代表UHPC整体钢纤维的取向分布。假设钢纤维形心位置距离横切面为z,空间Ω内钢纤维形心的概率密度函数[14]如式(1):
(1)
设空间Ω内钢纤维倾角为φ为事件A,则与纤维取向的概率密度函数p(φ)的关系如式(2):
P(A)=p(φ)
(2)
当倾角为φ的钢纤维与横切面相交时,其形心位置距离横切面小于lfcosφ/2,假设空间Ω内的钢纤维穿过横切面为事件B,则有:
(3)
则空间Ω内钢纤维穿过横切面概率如式(4):
(4)
图像分析测量得到的纤维倾角为φ的概率,实际上是指过横切面钢纤维中倾角为φ的概率,即P(A|B),笔者用psec(φ)表示。根据贝叶斯定理,可知p(φ)与psec(φ)的关系如式(5):
(5)
式(5)中P(B)包含了未知量p(φ),为了求解P(B),需要利用概率密度函数的性质,如式(6):
(6)
故P(B)的计算如式(7):
(7)
横切面图像处理分析得到的纤维倾角频率直方图可近似作为psec(φ)。根据式(5)、(7),UHPC内整体纤维取向分布频率直方图、及对应的均值φm如图8。由图8可知,R-UHPC和A-UHPC的纤维取向分布具有明显的差别。R-UHPC纤维倾角均值为56.9°,且大部分集中在50°以上,整体分布形状接近于cos函数;A-UHPC纤维倾均值为47.3°,明显小于R-UHPC的倾角均值,且主要分布在30°~50°间,整体分布形状接近于sin函数。
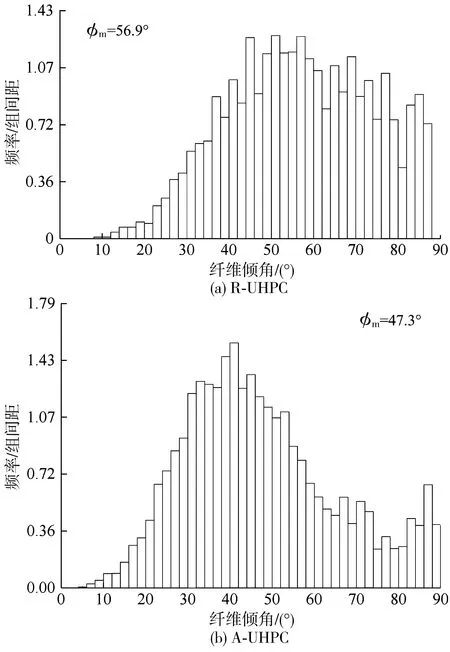
图8 整体纤维倾角频率分布直方图
3.2 纤维取向系数
图像处理分析不仅可以得到横切面上纤维取向的分布特征,同时也可以得到横切面上纤维数量。部分学者采用纤维取向系数θ[15]表征UHPC的纤维定向程度,如式(8):
(8)
式中:nf为横切面上纤维数量;Af为纤维的横截面积;Vf为纤维的体积掺量,笔者取Vf=0.03;A为横切面面积(抗折试件为100 mm×100 mm,轴拉试件为50 mm×100 mm)。
由式(8)可知,当纤维横截面积与纤维掺量一致时,纤维取向系数与单位面积的纤维数量nf/A(纤维密度)成正比。
图像处理分析统计得到纤维密度以及取向系数如表3。由表3可知,R-UHPC横切面上的纤维密度及取向系数明显小于A-UHPC横切面,后者与前者之比约为1.5。UHPC的抗拉强度以及阻裂性能主要由裂缝处纤维的桥联作用决定,式(8)中的nf表明,纤维定向浇筑对UHPC抗拉性能提升的主要原因是提升了UHPC开裂面处的纤维数量密度,从而整体提升UHPC的抗拉强度和开裂性能。

表3 UHPC纤维密度及取向系数
4 UHPC受拉性能
4.1 力学模型
UHPC受拉破坏发生在主裂缝处,通过主裂缝面的纤维桥联作用是承担拉力荷载的主要载体,可认为当UHPC达到极限强度时,所有荷载都通过主裂缝处的纤维传递[14]。因此UHPC的抗拉强度ft,UHPC可以用模型进行计算,如式(9):
(9)
式中:Pfi为极限荷载下过主裂缝面的第i根钢纤维承担的荷载。
单根钢纤维在拉拔作用下的极限承载力除了与纤维自生特性和纤维-基体界面粘接特性有关外,还与纤维的倾斜角度相关。考虑点触效应和基体压碎效应,文献[14]给出了单根纤维承担的极限承载力与角度间关系如式(10):
Pfi=ecφ(cosφ)kPf0
(10)
式中:c、k分别为纤维倾角的点触效应系数和基体压碎效应系数;Pf0为倾角为0的纤维极限承载力。
为简化计算,过切面的纤维所承担的荷载可以近似用倾角为均值φm的纤维计算荷载,则式(9)所述模型可以简化为式(11):
(11)
R-UHPC和A-UHPC的纤维密度和纤维取向系数成正比,因此式(11)中nf/A可以用纤维取向系数。假设R-UHPC的纤维倾角均值φm=φR,纤维取向系数为θR,A-UHPC的纤维倾角均值φm=φA,纤维取向系数为θA,故A-UHPC和R-UHPC的抗拉强度比值如式(12):
(12)
4.2 试验验证
试验测得的R-UHPC和A-UHPC的强度值如表4。由表4可知,A-UHPC的抗折和抗拉强度均显著大于R-UHPC,两者抗折和抗拉强度的比值都在1.6~1.7之间,说明纤维定向有效提升了UHPC极限受拉性能。2种UHPC的抗折与抗拉强度的比均维持在2.5左右,说明UHPC的抗折与C抗拉强度存在一个固定比,且该比值受纤维取向影响较小。

表4 UHPC受拉力学性能指标
纤维定向后的UHPC的抗裂强度得到了显著提升,A-UHPC与R-UHPC的开裂强度比值约为1.24,说明纤维取向不仅会影响UHPC开裂后的性能,同样也会影响纤维的阻裂作用,这与部分文献[4]、[7]一致。R-UHPC抗拉与开裂强度的比值约为1.1,A-UHPC抗拉与开裂强度比值约为1.47。可见R-UHPC在开裂后抗拉强度提升不明显,而A-UHPC在开裂后的抗拉强度提升显著。从破坏模式来说,普通方式浇筑的UHPC表现出明显的低应变硬化特征,纤维定向浇筑则使得低应变硬化UHPC能够转变为高应变硬化UHPC。
采用式(12)验算纤维取向对UHPC抗拉强度的影响,系数取值根据文献[14],c=1.6、k=1.8。故根据图像分析数据,A-UHPC和R-UHPC的抗拉强度比值为:
(13)
计算结果表明,评估模型得到的强度比值为1.69,与表5中试件测得的强度比值1.66十分接近,证明评估模型够精确评估纤维取向对UHPC抗拉强度的影响,且可以得到一个较为精确的量化值,是一个简单易用的评价指标。
5 结 论
通过UHPC的纤维定向试验和纤维取向图像分析讨论了纤维取向对UHPC抗拉强度的影响。通过上述试验和分析,可以获得以下结论:
1)采用通道流动结合振动的方式能够实现UHPC的纤维定向,普通浇筑下UHPC的纤维取向系数为0.487,接近0.5,纤维定向浇筑的UHPC纤维取向系数达到了0.731。
2)采用纤维定向浇筑方式的UHPC相较于普通浇筑的UHPC的开裂强度提升24%,抗拉强度和抗折强度分别提升66%、71%。
3)实测纤维定向使得UHPC的抗拉强度提升了66%,式(12)计算出的强度提升约为69%,排除试验误差和外界因素的干扰,可认为式(12)是一个可靠的用以定量评估纤维取向对UHPC抗拉强度影响的指标。

