一种基于贝叶斯推理的多标签数量估计方法*

刘 婷，陈庆荣，杨弘峰，宋金圣，韦 涛

（1.中国人民解放军93114 部队，北京 100085；2.电子科技大学，四川 成都 611731；3.中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引言

在射频识别（Radio Frequency Identification，RFID）系统中，同一时间内多个标签向读写器发送数据会发生冲突，这会严重影响通信的系统效率。RFID 系统一般都使用时分的接入方式，即节点竞争时间来发送，常见的接入方式可以归类为纯ALOHA、时隙ALOHA、帧时隙ALOHA 和动态帧时隙ALOHA（Dynamic Framed Slotted ALOHA，DFSA）。

DFSA 算法将信道分为多个时隙，标签随机选择一个时隙接入信道。根据每个时隙中活跃标签的数量不同，可以把时隙分为3 类，空时隙（0 个标签）、成功时隙（1 个标签）和碰撞时隙（多于1个标签）[1-3]。其中，只有成功时隙完成了信息的有效传输，系统效率为成功时隙占总时隙数量的比例。

当标签数量和时隙数量相等时，系统效率达到最优性能，为36.8%[4]。DFSA 算法性能除了受到标签数量估计精度的影响外，还受到初始时隙数量选择的影响。当初始时隙数量选择不合适时，会显著降低系统性能[5]。DFSA 提前停止算法在盘存过程中不断地估计标签数量，并实时地判断时隙数量和标签数量组合是否符合最优组合。如果不符合，则提前停止该帧并立即更新时隙数量[6]。

提前停止算法降低了初始时隙数量选择不合理带来的影响，但是仍然存在一个观察时隙的问题。传统的标签数量估计算法需要观察多个时隙中标签是否成功传输或碰撞。一般说来，观察的时隙数量越多，标签数量估计的准确性越高，不同的观察时隙的数量会影响算法的性能[7]。Robithoh Annur 等提出了一种贝叶斯估计的算法，可以只观察一个时隙来估计标签数量，并在连续的帧迭代过程中不停地更新标签数量估计的值，既可以达到优秀的标签数量估计精度，又可以减少观察时隙的数量，其系统性能在标签数量较多时（N＞200）可以达到DFSA的理论极限，但是其计算复杂度较高[8]。

本文在贝叶斯估计算法的基础上进行了改进，拟降低其计算复杂度，并提高算法在标签数量较小时的性能。该算法采用贝叶斯推理的方式，根据先验概率和似然函数计算后验概率，在贝叶斯推理的基础上，进行了两个改进。第一，在计算先验概率和后验概率时，采用了动态调整计算区间的方法，降低了初始计算区间对算法复杂度的影响；第二，采用正态分布对先验概率进行拟合，降低了计算复杂度。仿真结果显示，该算法性能与原始算法相当。

1 系统模型

在DFSA 系统中，读写器开启一个包含若干时隙的帧，标签会随机选择其中的一个时隙来传输。在本论文中，将时隙ALOHA 接入方式看作是特殊的DFSA 接入方式，每一帧只有第一个时隙被实现，即每一帧在其第一个时隙后就提前结束。如图1 所示，读写器首先开启了长度为4 的帧，在第一个时隙结束后重新开启了长度是16的帧，后面的帧以此类推。每个帧实质上只有第一个时隙，其余时隙都没有实现。每个帧只有选择了第一个时隙的标签才会发送。在DFSA 系统中，节点数目的估计算法和帧长的调整策略是两个重点，严重影响着系统的性能。为了最大化系统效率，读写器可以在每个时隙都估计标签数目，并且据此更新帧长度和接入概率。

2 贝叶斯推断

在一个帧内，每个时隙内只有3 种情况，即空时隙、成功识别的时隙、冲突的时隙。3 种时隙的数目分别表示为E、S、C。读写器可以根据这3 种时隙的数目来估计节点的数目。

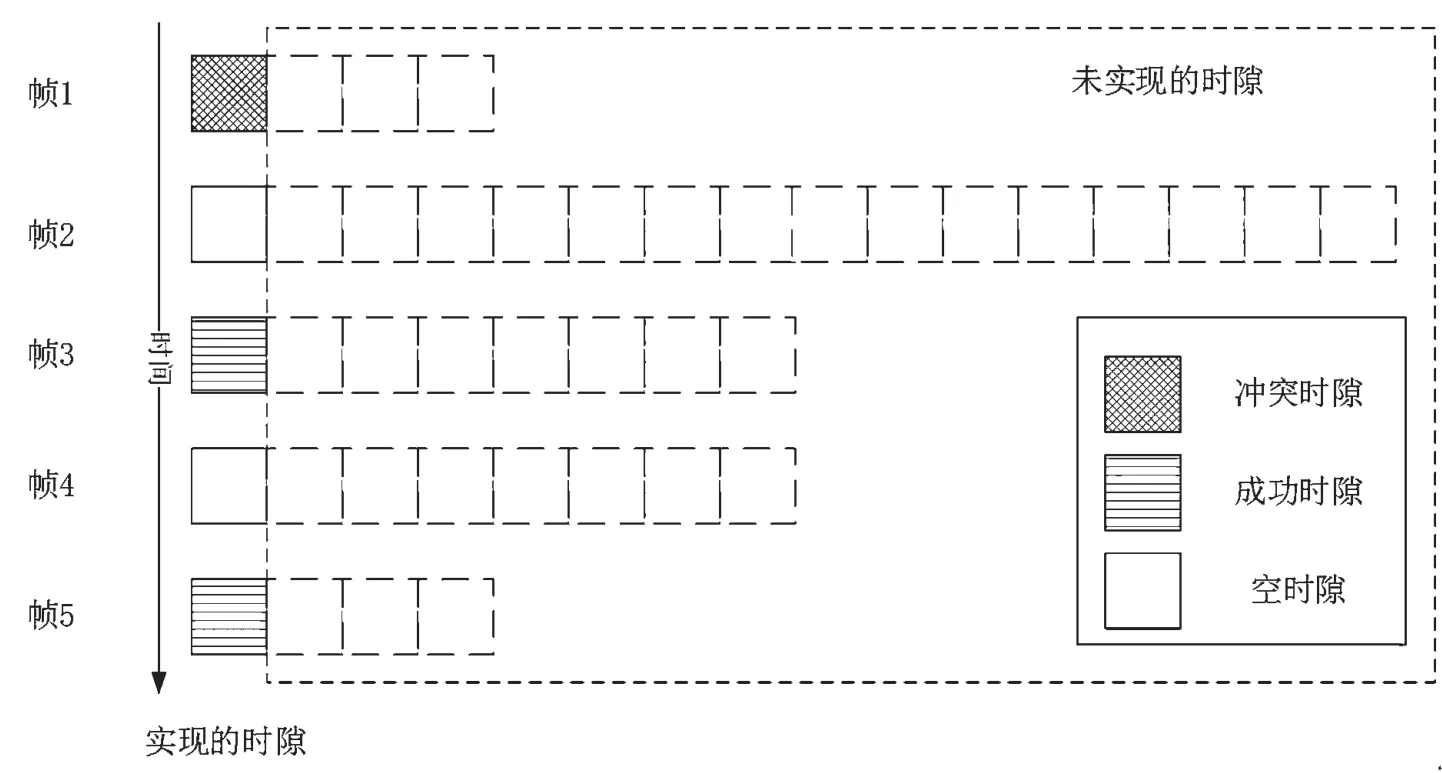
图1 系统模型结构

贝叶斯推断利用贝叶斯定理，根据先验条件来估计后验概率。在DFSA 系统中，可以使用贝叶斯推断来逐时隙地估计标签数目。将当前时隙中发送的标签数目作为先验信息，读写器工作范围内要识别的标签数量作为参数N，则先验概率表示为P(N)，N的范围是[0,∞]。在每个时隙内，假定标签接入的概率是p，则似然函数可以表示为式（1），其服从二项分布，其中F是当前时隙中的标签数量。

根据贝叶斯公式，可以将后验概率表示为：

由于在每个时隙中F是独立同分布的，结合Bernstein-von Mises 定理可知，后验概率会收敛于正态分布，对式（2）求期望可得到式（3），可以用来估计N。

尽管贝叶斯推断具有较好的估计性能，但是在DFSA 应用中会存在一些限制。一方面，读写器无法确定N的大小，在计算时假定N分布于[0，∞]是不切实际的，如果假定其分布于0 到Nmax，在实际标签数目大于Nmax时该算法将不适用。另一方面，读写器需要记录所有后验概率的值，并且在每个时隙根据似然函数和观测数据来计算后验概率，每个时隙中至少要进行2Nmax次乘积运算，运算量较大并且与标签数目相关。为此，本文基于贝叶斯推断提出改进算法，使用高斯函数来估计后验概率，每次计算只有两个主要参数进行更新，明显降低了计算量。

读写器在每个时隙都计算最优帧长。最优帧长可以根据标签数目的估计值来确定。如果最优帧长与当前帧长度相同，读写器会发送QuerryRep 命令继续执行当前帧，否则发送QuerryAdjust 命令调整帧长度。在服从EPCglobal C1G2 标准的情况下，帧长只能是2 的指数，即2Q，否则帧长可以是任意的自然数。在一次盘存过程中，读写器重复执行上述命令，如果读写器开启了一个长度为1 的帧并且没有标签发送，则表示所有标签都识别完，盘存过程结束。

3 改进的贝叶斯算法

高斯分布仅仅由期望μ和标准差σ决定。使用高斯分布来近似模拟后验概率曲线可以简化计算，不用记录后验概率的所有值，每次只需要关注更新μ和σ两个变量及分布区间[0，Nmax]。假定先验概率服从高斯分布，对似然函数进行选择，可以保证后验概率曲线保持高斯函数的形状。需要注意的是，使用高斯函数来近似分布区间里的后验概率曲线，并不意味着标签数目服从高斯分布。考虑到分布区间的变化，在分布区间内，对概率进行了归一化以确保在每个时隙中其和为1。

使用μc和σc表示在当前时隙中对未识别节点数目估计的期望和标准差，μn和σn表示下一时隙中的期望和标准差，F表示当前时隙中的标签数目。由于读写器不能区分冲突时隙中的节点数目，时隙为空、成功、冲突3 种状态分别对应为F=0、F=1、F＞1。对于空时隙，似然函数是关于N的指数函数，后验概率可以表示为：

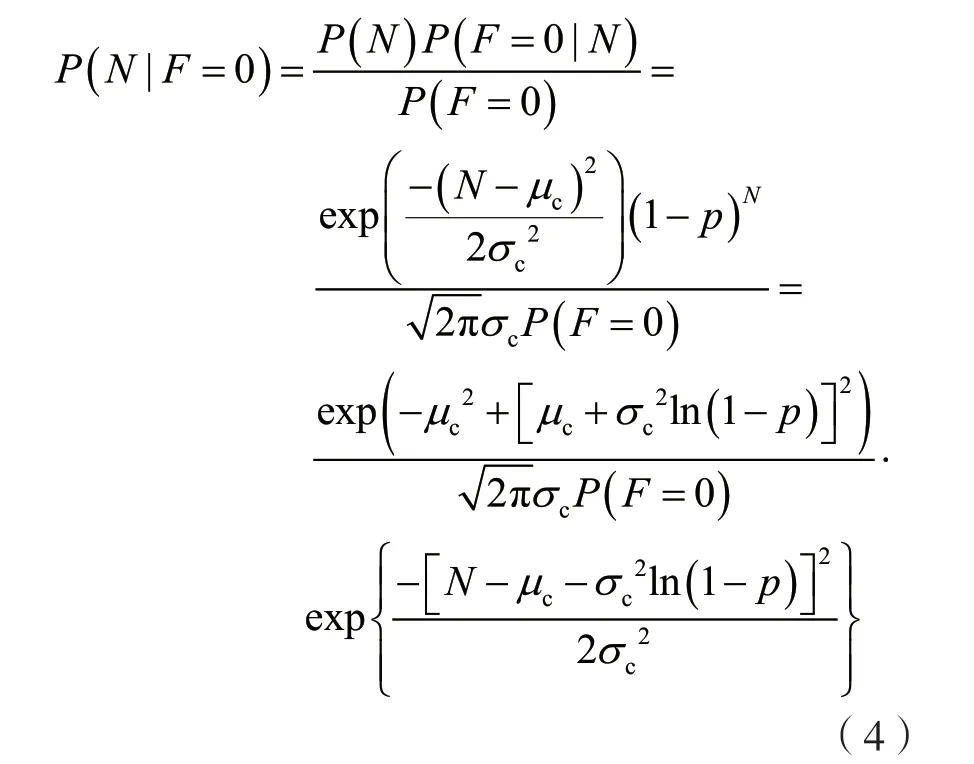
明显可以看出后验概率仍然是高斯函数，根据当前时隙的期望和标准差可以估计下一时隙的期望值：

假定了p足够小，使-ln(1-p)≈1/p。

对于成功的时隙，期望和标准差分别由式（6）和（7）得出：

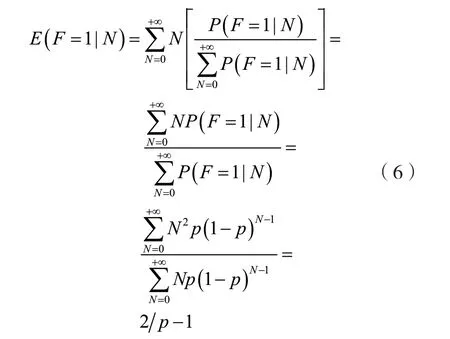
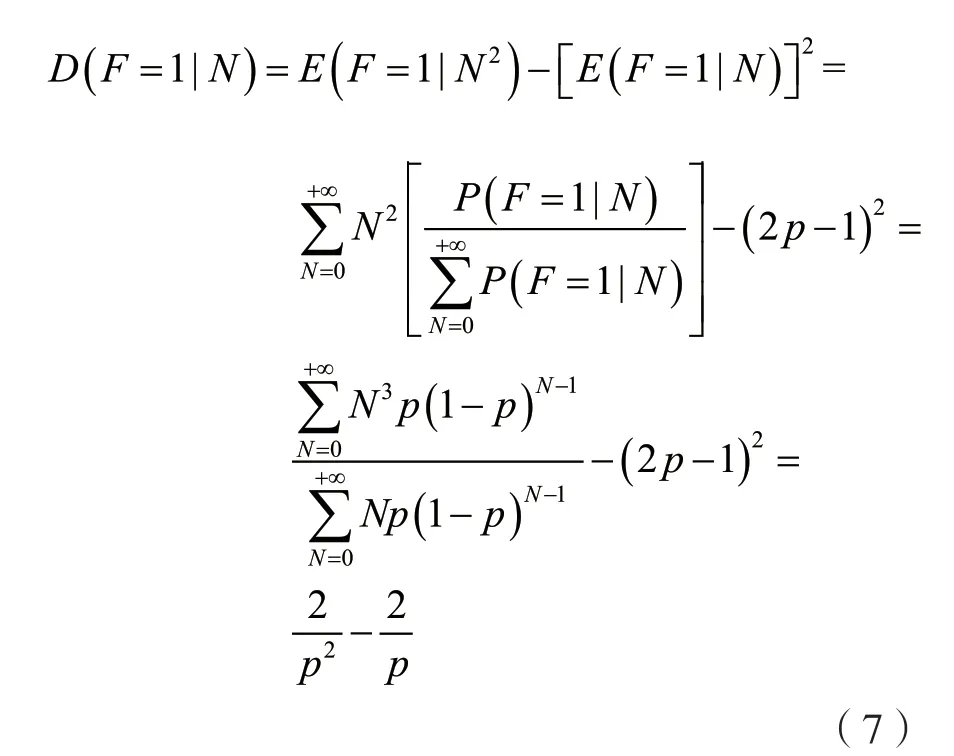
当时隙中F＞3 时似然函数是类似log 函数的曲线，1 ≤F≤3 时似然函数是∩形曲线，此时期望和标准差可以表示为：

和空时隙的情况类似，后验概率仍是高斯函数，结合贝叶斯公式，后验概率表示为：

对于成功时隙，即F=1 的情况，由于只对未识别的标签数目进行估计，要在后验概率的期望值上减1，由此得到更新的后验概率的期望和标准差：

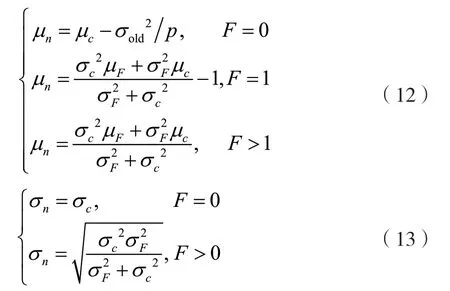
根据后验概率的期望、标准差和分布区间来估计未识别的标签数目，其中erf(x)是高斯误差函数。

为了保证算法适应不同标签数目，每次估计需要对分布区间做出调整，Nmax的更新公式为：

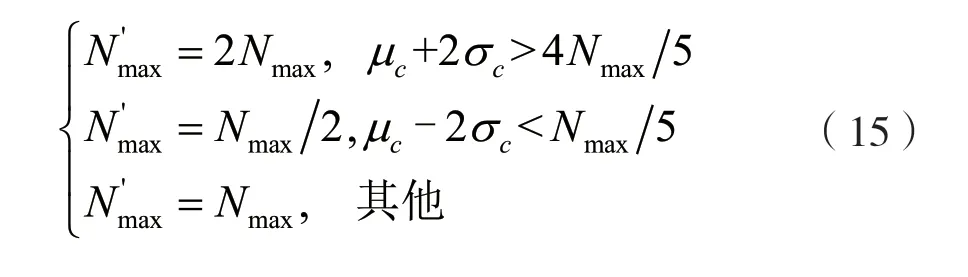
4 算法仿真

首先评估提出的算法对初始Q值的敏感性。作为对比，采用文献[1]中的标签数量估计算法，并对标准DFSA和DFSA帧提前停止算法进行了对比。仿真结果如图2 所示。从图2 中可以看出，当读写器不采用帧提前停止算法时，即使读写器准确地知道标签数量，也无法达到最优性能，系统性能在初始Q值和标签数量匹配时才达到最优。而当采用了帧提前停止算法时，则算法对初始帧长和标签数量的敏感性明显下降，对于不同的初始Q值，系统的性能也存在一定的波动性。而本文提出的算法则能很好地应对初始帧长和标签数量不匹配的问题。

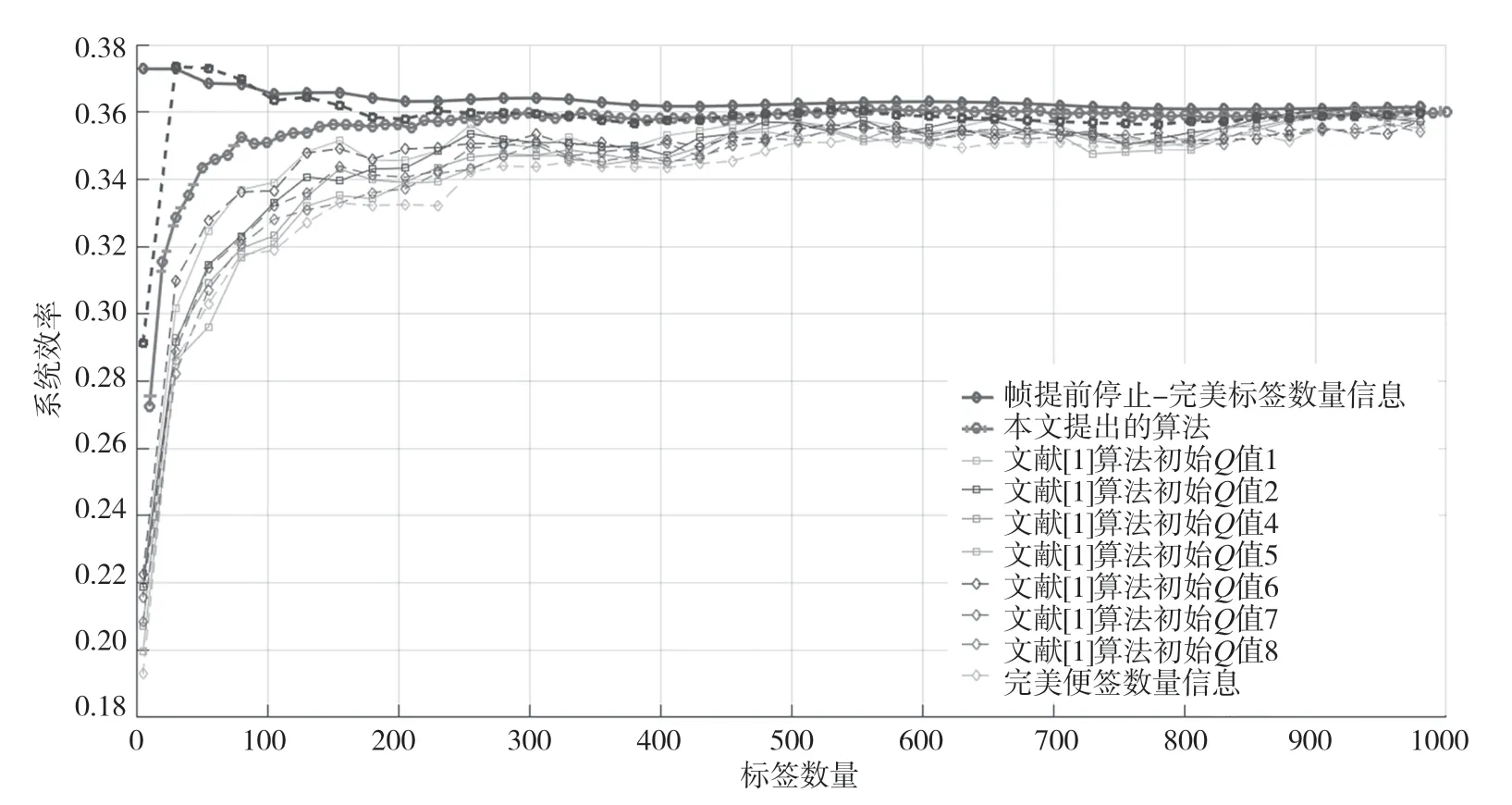
图2 性能仿真结果

5 结语

本文提出了一种改进的基于贝叶斯推理的RFID 标签数量估计算法，该算法利用高斯函数来拟合先验概率，在每个时隙结束时根据时隙的类型，利用式（8）、式（9）、式（11）、式（12）和式（13）来更新μ和σ，及估计标签数目。算法收敛快，估计精度高，可以应用于DFSA 帧提前停止算法中。仿真结果表明，该算法系统性能稳定，对标签数量和初始Q值不敏感，大大增强了RFID 系统的稳定性。此外，该算法与传统贝叶斯估计算法相比，复杂度大大降低，仅需要进行固定数量的基础运算。本算法适用于大容量仓储物流中多标签高效快速识别应用场景。