基于深度学习的单多载波信号识别方法*
杜志毅,李保国,张澄安,徐 强
(国防科技大学,湖南 长沙 410073)
0 引言
正交频分复用技术(Orthogonal Frequency Division Multiplexing,OFDM)是一种在通信领域有着广泛应用的多载波调制技术。随着通信技术的迅猛发展,在复杂电磁环境下,信号调制方式识别对信号的后续处理解调显得十分关键与紧迫。
OFDM 信号是一种多载波调制信号,这导致其识别过程与其他单载波调制信号不同。识别OFDM信号首先需要确定接收到的信号是单多载波信号中的哪一种,因为这是解调OFDM 信号过程的先决条件,也为识别其他单载波信号提供了帮助。
现有关于调制识别的大多数技术一般都是基于特征提取和机器学习分类算法[1-2]。但这些方法多数为模型驱动,需要对信号进行预处理,其适应信道环境单一,因此在复杂信道环境时识别性能较差。另外因为传统的特征提取方法是基于统计资料[3],所以分类结果易受环境变化影响。然而,基于机器学习的调制识别方法也是需要人为提取信号的特征,不能像深度学习方法自主提取出信号特征。所以这些方法在复杂信道环境下识别准确率不会很高。
深度学习的方法[4-5]被认为是突破性能瓶颈的有效方法[6]。在此基础上,本文提出了一种基于改进的ResNet 深度学习网络的调制识别方法(Improved ResNet based Modulation Classification method,IRMC)。IRMC 采用了缩放指数型线性单元SeLU 激活函数来对抗Dead ReLU 的问题,并且降低了卷积核的大小,大大减少了运算的复杂度。实现了单载波信号和OFDM 信号的有效区分。
本文以下内容共分为4 个部分:第1 节介绍系统模型和OFDM 信号模型;第2 节介绍识别算法;第3 节给出仿真结果,通过不同方法之间的性能对比来验证本文提出方法的可行性;第4 节对本文进行总结。
1 系统模型
1.1 系统结构
图1 展示了OFDM 信号识别的系统架构。信号源的信息通过OFDM 调制转换为OFDM 信号,通过信道进行传输。本文设置了以下3 种信道环境进行实验:高斯信道、多径信道与复杂莱斯多径衰落信道。
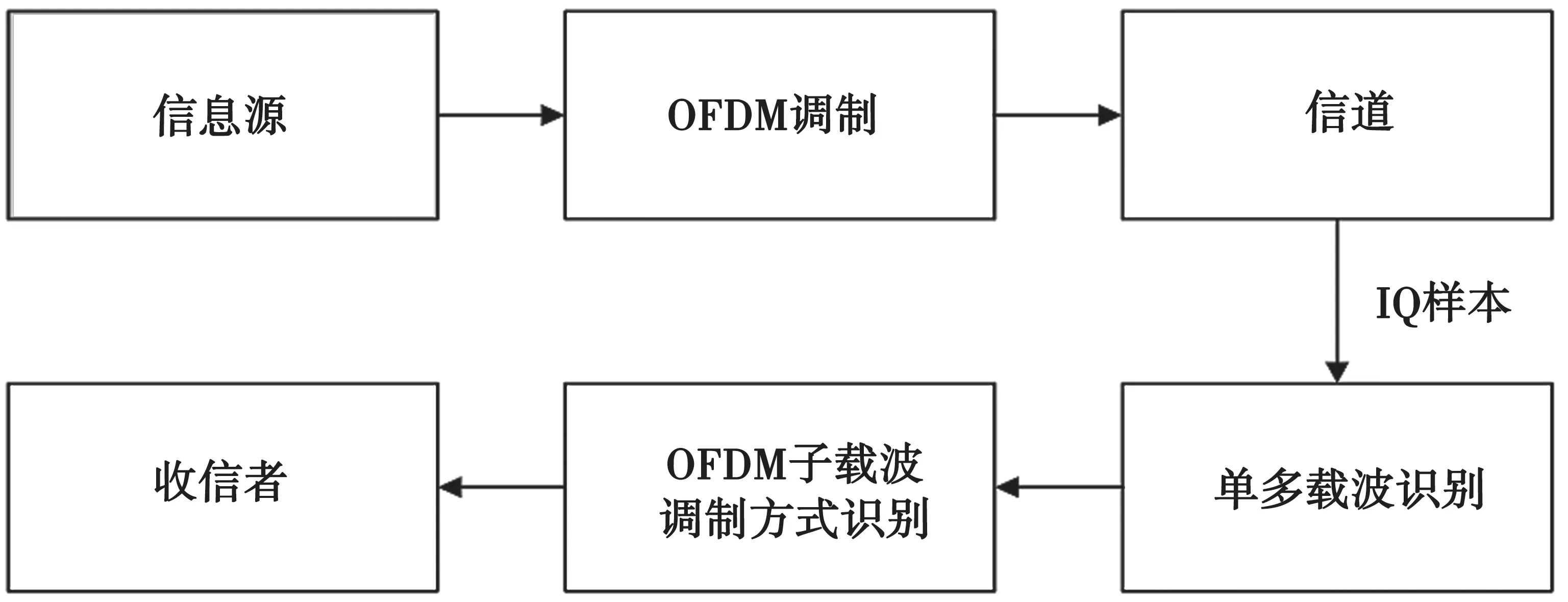
图1 OFDM 信号识别系统结构
本文采用信号的同向正交IQ 序列进行识别,考虑接收到的信号经过下变频和匹配滤波得到基带复信号,IQ 序列则分别代表接收到信号为2×K大小的实值矩阵:
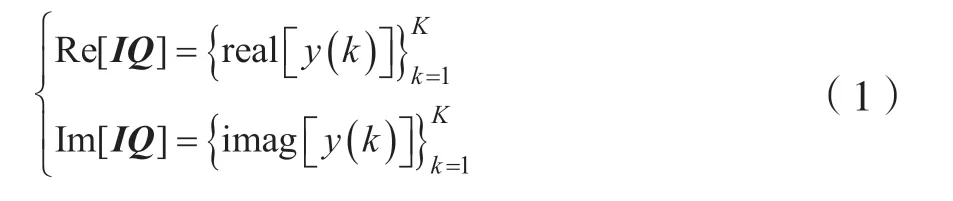
1.2 OFDM 信号产生
OFDM 系统的原理框图如图2 所示。
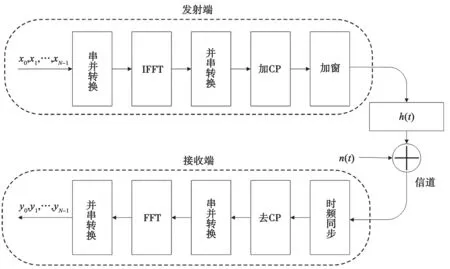
图2 OFDM 系统原理
OFDM 系统主要是源于多载波调制与模拟调制的频分复用技术。在连续信号模型中,某个频率值为fk的信号ϕ(t)为:

式(2)中,fk=f0+k∆f,f0是初始频率,∆f是频率间隔,Xk是频率fk处的幅度。累加N个频率上的值得到式(3):
假定t=nTs,对式(3)进行采样周期Ts的采样则实部和虚部如式(4)所示:
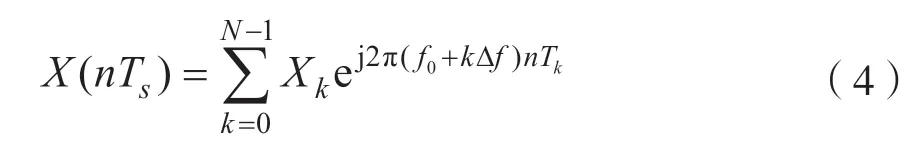
令f0=0,∆f=1/nTs,式(5)则为:
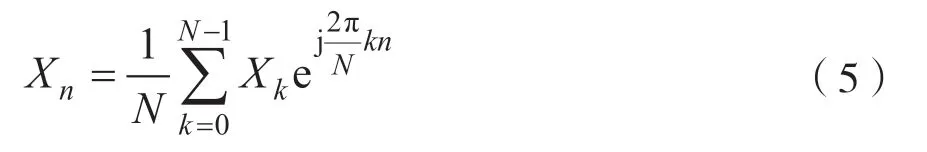
式(5)中,增加系数1/N使离散化后信号功率恒定。该式即为OFDM 基带调制信号的表达式。
2 识别算法
2.1 网络结构
本文使用的深度学习网络是在经典深度残差网络(Deep Residual Networks,ResNet)模型[7]上进行改进的,将除了第一个Residual Stack 单元之外的其余Residual Stack 单元中卷积核设置为3×1 大小,这样可以大大减少参数数量。
模型的结构如图3 所示,其中Residual Unit 就是残差网络中的残差块,即ResNet 原始单元结构,由线性卷积层、卷积层ReLU 激活函数与跳跃连接(即恒等映射)组成,能够很好地防止由网络层数增加而导致的退化及梯度弥散问题。
另外在残差块的基础上,构建了Residual Stack单元。每个Stack 单元包括一个卷积核大小为1×1的卷积层,用于channel 维度上的计算,此外还包含两个残差块,以及一个最大池化层(Max Pooling)来减少特征图尺寸。在整个模型中一共包含6 个Residual Stack 单元,数据每经过一个Residual Stack 单元维度减半。模型中所有卷积层的卷积核数量均为32,卷积核大小3×2。
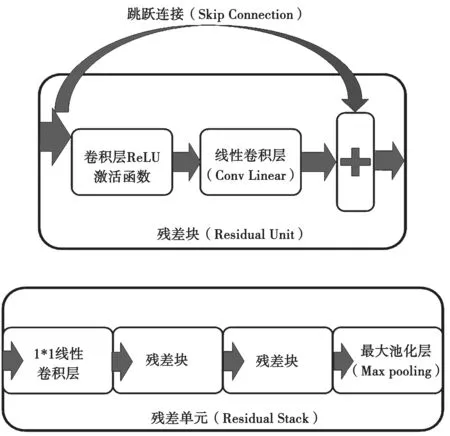
图3 IRMC 网络模型结构
本文所提出IRMC 网络参数表如表1 所示。

表1 IRMC 网络参数
输入为2×1 024 大小的同向正交IQ 序列,通过6 个Residual Stack 单元后输出为32×16 大小的特征图,最后经过全连接层输出分类结果。网络中Residual Stack 单元都是使用ReLU 激活函数,最后的全连接输出层采用Softmax 激活函数,值得注意的是两层全连接层并没有采用ReLU 激活函数,而是使用了缩放指数型线性单元SeLU 激活函数[8],其表达式如下:

SeLU 激活函数带有自归一化属性,可以归一化映射前后的两层神经网络的均值和方差。其相比于ReLU 激活函数不会产生Dead ReLU 的问题,输出均值接近0(zero-centered)。
经实验测试发现在信号调制识别这种计算量不是很大的情况下,表现比ReLU 激活函数优异。网络优化过程中,采用Adam 算法进行网络参数的最优解求解。
2.2 数据集制作
本节主要介绍训练样本集的生成,图4 为本文样本集构造流程。为使样本足够丰富多样,本文设置了3 种信道环境进行数据集的制作。在研究初期,为了更好地控制信号的质量,信号集利用MATLAB平台产生。

图4 样本集构造流程
2.2.1 特定调制模式与随机比特数据
仿真数据集为2×1 024 大小的IQ 序列,本文所需识别的调制类型集包含单载波信号与多载波信号即OFDM 信号两个种类,其中单载波信号包含以下11 种常见单载波信号,按顺序分别为:BPSK、QPSK、8PSK、QAM16、2FSK、MSK、FM、AM、ASK2、FSK4、OQPSK。信号码元由MATLAB 生成随机比特数据进行调制。
OFDM 信号采用IEEE802.11a 标准产生[9],载波数目有52 个,其中4 个作为导频,48 个作为数据子载波。采用20 MHz 信道带宽,OFDM 符号持续时间为4 μs,保护间隔为0.8 μs,占用带宽16.6 MHz。
2.2.2 标准信号的生成
数字信号中心频率在902 MHz,模拟信号中心频率在100 MHz,脉冲成型滤波器采用根升余弦成型滤波器(rcosdesign 函数),其滚降系数为0.35,初始相位在0~2π 范围内随机选择,采样频率是200 kHz,每个符号采样点数为8,单个样本长度为1 024,每一帧长度为1 024/8=128。OFDM 信号子载波调制方式为BPSK、QPSK、8PSK、16QAM 这4 种随机。
2.2.3 信道环境
信道环境为3 种,第一种为理想高斯白噪声信道,第二种考虑简单多径信道(多径幅度为[1 0.2 0.1],多径时延为[0 20 50]),第三种为复杂莱斯多径衰落信道考虑了采样率偏移,中心频率偏移(MaximumClockOffset=5),最大多普勒频移(MaximumDopplerShift=4),莱斯多径衰落信道(平均路径增益=[0 -2 -10]dB,延迟分布=[0 1.8 3.4])。
信噪比范围为0~20 dB,步进为2,单载波信号每种调制方式在每种信噪比下样本数目为400个,样本数48 400 个,多载波信号在每种信噪比下样本数目为4 400 个,样本数48 400 个,总样本数共计96 800 个。
3 性能测试与分析
深度学习的环境语言配置为Python 3.7,TensorFlow 1.14.0,Keras 2.3.1,计算机设备为CPU:E5-2630,GPU:2080T。
整个数据随机(固定随机种子)将其划分为训练集和测试集,比例为8:2。批尺寸batch size 为64。本文中定义的调制识别性能识别率为:

3.1 识别结果
本文采用Walter Akmouche[10]的经典算法作为传统方法进行对比,该算法利用4 阶高斯累积量进行单多载波识别。首先在最为理想的情况下,直接仿真产生单载波基带信号无需进行采样滤波操作,经过高斯白噪声信道后就进行识别。其结果如图5所示,在这种情况下传统方法的识别率较高,在4 dB 时OFDM 信号的识别率能够达到90%,而本文则是采用的是实际应用中的信号生成流程。

图5 单多载波识别-OFDM 信号识别率(理想情况)
如图6 所示,对于同样的高斯白噪声信道,传统方法在面对采用标准信号生成流程产生的信号时识别率有了明显的下降,在13 dB 的情况下才达到90%的识别率。
这是因为信号经过上采样与成型滤波后,信号的高阶累计量特性会发生一定的变化,导致其稳定性下降,即使在20 dB 的高信噪比条件下,其识别率也只能达到95%,而不是100%。但这并没有影响到IRMC 的识别性能,依旧在0 dB 时就达到100%的识别率。

图6 单多载波识别-OFDM 信号识别率(实际情况)
对于简单的多径信道,传统方法识别率有所下降,IRMC 方法则没有造成明显的影响,识别率与高斯白噪声信道相差无几。而对于复杂的莱斯多径信道,两种方法的识别率均出现了明显的下降,这是因为信道中添加的干扰所造成的。IRMC 识别率虽然有了大幅度的下降,但传统方法在20 dB 时只能达到87%的正确识别率,对比传统方法有还是有明显提升。
在三种信道环境下,IRMC 的识别效果都要好于传统方法。这是因为传统方法只是通过高阶累积量来进行单多载波识别,易受到信道环境的影响导致识别率下降。而深度学习的方法不是通过单一特征进行识别,深度学习网络可以通过卷积层得到许多关于信号的特征,利用提取出的所有特征进行识别分析,所以在应对复杂的信道变化时,比单一使用高阶累计量进行识别的传统方法表现要更加优异。
本文以85%识别率的情况下,IRMC 相比于传统方法的信噪比增益来量化识别性能的优劣。综上所述,复杂莱斯多径信道上IRMC 相比于传统方法在85%识别率下能够达到10 dB 的信噪比增益。
3.2 泛化性检测
深度学习的泛化性不强一直是亟待解决的问题,为验证IRMC 的泛化性能力,本文对复杂信道环境中的不同参数进行调整,通过调整后的数据集对模型进行测试。结果如图7 所示,改变信道的5 种参数分别为:采样率(200 MHz 变为250 MHz)、多普勒频移(4 变为6)、平均路径增益([0 -2 -10]dB变为[0 -5 -15]dB)、时钟偏移(5 变为3)、信道路径延迟([0 1.8 3.4]变为[0 3.5 6])。可以看出在改变信道参数环境后,识别率有所下降,但下降幅度较小,在5 dB 时识别率下降最大,但也仅下降了5%。可以得出结论,本文提出的IRMC 在单多载波识别上有着较好的泛化性能,可以适应信道环境的变化。

图7 深度学习泛化性对比
3.3 算法时间对比度分析
表2 给出了不同算法对目标信号识别的时间复杂度,实验结果是对20 000 个样本的识别时间进行统计平均得出的。表中显示,传统方法的时间复杂度是低于深度学习方法的,这是因为人工特征提取是有指导性的,而深度学习方法则需要自主学习。但现在GPU 并行运算能力大幅提高,可以并行完成神经网络运算,所以深度学习方法可以通过并行计算减小计算开销从而提高计算速度,最终实现快速运算。

表2 不同算法信号识别过程的时间复杂度
另外对比经典的ResNet 网络[7],IRMC 的信号识别过程时间有着明显的降低。这是因为IRMC 单元中卷积核设置为3×1 大小,大大减少了参数数量。总体可以看出,本文提出算法的运行时间在毫秒级别。虽然高于传统方法,但相较于经典ResNet网络有着明显降低,可以满足实时处理的要求。
4 结语
本文提出了一种基于改进的ResNet 深度学习网络的调制识别方法(IRMC),较好地解决了传统方法需要预处理和在复杂信道环境下识别性能较差的问题。仿真实验表明,本文提出的方法应用于单多载波识别上,能够明显提高识别性能,在多种信道环境下都有着优于传统方法的识别效果。IRMC 仅利用信号的IQ 序列进行学习分类,降低了卷积核的大小,大大减少了运算的复杂度,算法时间可以满足实时性处理的需求,是有效可行的。

