数理统计与数据分析在卷烟产品质量检测中的应用

关 斌，常 宇，张常记，李 强，叶 茵，徐淑浩，李慕颜

（1.红云红河烟草（集团）有限责任公司 红河卷烟厂，云南 弥勒652399；2.四川中烟工业有限责任公司什邡卷烟厂，四川什邡618400）

0 引言

数理统计是用数学统计分析的方法来解决实际问题的学科，属于数学研究领域的一类分支，能够通过对事物的观察来找到现象发生背后的规律，然后利用统计数据来做出预测。数理统计已经变成了多个不同学科发展过程中的重要内容，通过选择合适的统计分析方法，能够对试验得到的海量数据进行深入分析，从这些数据当中提取出规律，然后作为后续工作的指导意见。通过数据分析能够获取产品的详细信息，并且在生产过程中严格把控多个不同的环节。在数理统计学科应用到实际生活的过程中，需要人们根据实际的需求来采取合适的统计分析方法。有关于数理统计的理论基础早在20世纪就已经初步形成，但是一直到计算机诞生之后才被广泛地应用于多个不同学科。在检测方面，试验分析是一个非常重要的环节，若是缺乏试验分析，就无法对所做的研究进行仔细分析，也很难从海量的数据里面找到相应的规律，无法提供给决策足够的参考信息[1-5]。对数理统计与数据分析在卷烟产品质量日常检测实验中的应用作介绍性交流，以期实验室检测人员对数理统计与数据分析方法的重视和运用。

1 数据的整理

在对产品进行检测的过程中，机器会输出各类不同的数据。这些数据不仅囊括了产品的各项指标，同时也可以从中找出规律，帮助更好地发现问题。但是，这些初步输出的数据是需要分析之后才能为研究者所用。在海量的数据当中去除那些无效的信息，而将有效的信息进行梳理分析，这样才能够最终获得想要的内容，做出更为准确的决策。

例如，烟草质量监督检测站日常的检测工作中，以卷烟成品检测对烟支圆周指标检测数据分析为例，如果检测200支卷烟，就会得到200个圆周数据，这些数据肯定有波动，但肯定也有规律可循。

（1）样本均值（x）极差（R）、标准偏差（S）等值越大，那么波动也会越大；该数值可以较为准确地反映出数据的波动大小。简单的数学统计就可以知道数据的变化规律，还可以通过划分范围来归纳统计，如划分出卷烟品牌、某机台生产的烟支、某种机型生产的烟支，再相互比较圆周的差异变化。

（2）需要了解更为完整的波动规律，则需进一步归纳出频数分布和正态分布函数：

此公式表示样本落入（a，b）区间内的概率等于（a，b）横坐标和曲线所包含的面积，其中σ越大，曲线越宽，说明数据越离散，反之则越集中。

（4）显著性检验，也称为假设检验，对于H0，假设x=μ，观测值和已知值没有差别，当H0被拒绝，其对立的H1则被接受。这2个不同的均值一般是利用t检验来进行对比的，如果是多个样本均值，那么是需要用F检验来完成，某事件频率的比较则用x2检验。这些检验方法较常用且有效。

如日常检测分析烟草原料中总糖含量（%），检测结果为：

近红外光谱快速检测法得到的数据为x2=23.8，S2=0.28；

化学流动分析检测法得到的数据为x1=22.4，S1=0.21；

2种方法均进行了10组检测，即n1=n2=10；S2=0.0613；

自由度为18，若p=0.05，查表得t0.05=2.1，则t＞t0.05，由于t＞t临界，则拒绝H0。

假设检验表明2种方法比较有显著差异，需要重新校正近红外模型。而F＜F临界=4.026，表示这两类不同的检测之间不存在统计学意义上的标准 误差。

（5）异常值的检验[5]，在梳理分析数据的时候，常常会碰到这样的情况，就是在一组数据里面会发现个别跟均值相差较大的数据，这些数据一般被分析者叫做是异常值，通常是因为在试验过程中的错误操作而造成的。在处理异常值的时候要谨慎，需要找到该数据产生的原因，如果是正常操作那么也需要纳入最后的统计当中，能够来统计分析异常值的检验方法有很多，最为常用的有格拉布斯检验法及奈尔检验法等，分别适用于未知偏差及已知偏差2种不同的情况。

以狄克逊单侧情形检验为例：

将n个测定值按小到大的顺序排列

可能的异常值：x（1）或x（n）。

若统计量f0＞f（α，n），则应剔除x（1）或x（n）。

从上面的算式当中，可以知道每次检测只能够处理一个异常值。在删除异常值之后，其最终的测定数量也需要进行再一次确定，一直统计处理到没有。具体的临界值等信息可以参考表1。

狄克逊检验临界值（单侧部分）和统计量计算公式见表1。

表1 狄克逊检验临界值（单侧部分）和统计量计算公式

2 通过数理统计找出对结果有直接影响或影响较大的因素

主要有2种方法：方差分析和回归分析。

2.1 方差分析

一般被叫做变异系数分析，通常是需要将观察值所产生的变异进行分类。利用单因素方差来对某个因素所造成的变化进行统计，如几种不同卷烟加工工艺作用同一卷烟规格样品，每种工艺方式作用4个卷烟样品，对样本的主流烟气焦油量考查表示如下：

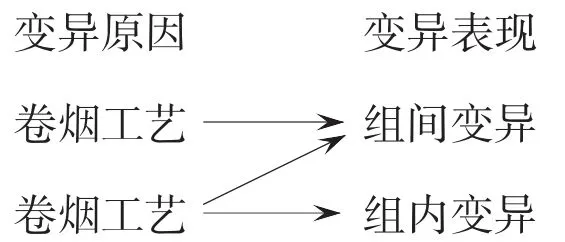
通过考查数据，发现卷烟加工工艺对组间变异影响较为显著，进而考查哪种工艺对降低焦油量作用明显。

还有双因素和正交方差分析，可以从多个影响因素中筛选出更为显著的主要因素，考查影响因素之间有无交互作用。例如，按照烟草行业企标《YC/T 161—2002烟草及烟草制品 总氮的测定 连续流动法》规定的方法来进行总氮的测定，其化学原理为：首先，将烟草或烟草制品在浓硫酸和相关催化剂的辅助下，经过消化分解，待检测物中的氮全部会转换成氨，然后加入次氯酸钠，在碱性环境下，氨被氧化为氯化胺，接着跟加入的水杨酸钠进行反应，最终产生靛蓝染料，接着进行比色测定，可以看出浓度会跟吸光度表现出正比关系，就可以得到氮含量。在此测定的过程中，会有多种不同的因素影响浓度值结果，如催化剂的使用量、消化程度及硫酸用量等，这些因素不可避免地会影响到测定结果。观察这些因素所引起的误差进行统计分析，可以得到影响较大的因素。

2.2 回归分析

可以通过该分析方法来明确各类因素之间存在的关系，并且以回归方程的方式来进行预测，最终得到因变量所产生的变化，有些是可确定的函数关系，有些是不确定的相关关系。按照因变量跟自变量的数量可以将回归分析分为一元分析及多元分析两类。按照函数表达式的不同可以分为线性分析和非线性分析两类。

在许多仪器检测定量分析中，经常要使用到回归分析，物质的浓度（或含量）与吸光度、峰高、峰面积、谱线的强度等具有相关关系，根据不同浓度x产生对应的y值，建立线性回归方程y=a+bx，并通过：

当|r|=1，意味全部测试点落在直线上，r2表示由x说明y的误差在总误差中的比例，r2越接近1，则线性拟合回归的越好。

3 试验的设计与优化

化学分析中经常需要进行方法的选择与优化，如反应条件的优化；在色谱分析当中筛选色谱柱、柱箱温度的选择与调整、设备操作参数的设置等，这些条件都需要试验的设计和优化。如何得到既能使分析过程稳定、结果准确，又能节约资源、人力、物力，并且无污染的方法呢？首先，试验设计的目的就是要使试验指标达到最优，要求指标具有可比性，把有影响因素的定性指标定量后以具体数值表示，统称目标函数据。一般将能够影响试验结果的因素叫做因子，并且将因子在试验过程当中的状态叫做因子水平。例如，在进行不同温度影响胶黏度的试验当中，温度的高低就是因子的不同水平，将其设置为3个梯度，分别为25，50，80℃，则温度因素有3个水平。如果所选因素的水平发生变化时，没有引起观测指标的变化，则表明所选因素没有影响，应从试验中剔除，重新进行因素的选择。以表2为例：

胶黏剂中乙酸乙烯脂含量试验（按卷烟胶的固含量降序排序）见表2。

表2 胶黏剂中乙酸乙烯脂含量试验（按卷烟胶的固含量降序排序）

由表2中数据可以看出，胶黏剂中固含量的大小与乙酸乙烯脂的含量大小没有显著的线性关系，与pH值和黏度也没有显著相关关系。影响胶黏剂中乙酸乙烯脂含量的因素需要重新选择其他因素来考查，比如胶黏剂生产合成过程中的反应条件，合成中使用的化学试剂及用量等。

根据试验方式的差异，可以将试验分为同时及序贯2种不同的类型。前者主要是指在试验的过程中对考查因素进行同时设计，这样可以得到各个因素水平的最终数据，根据数据来进行分析，试验不分前后，也不会相互影响。一般有正交试验、配方试验等类型。而后者属于一种单纯形优化法。

4 实验室能力验证结果的评价

认可实验室按照国家认可委的《能力验证规则》要求需定期参加能力验证试验[6]。适合的数理统计方法的选择决定了能力验证评价的公正力。通过认可的实验室检测人员应该掌握能力验证试验结果的统计处理方法和评价规则，以便读懂试验组织者公布的结果报告。

如果用常用的平均值作为参考值的比较方法，其缺点是当出现个别特别大或特别小的离群值时就会歪曲测量结果。在没有参考值可以利用的情况下，为了避免离群值的不良影响，在检测实验室的能力验证中，通常采用一些受离群值影响较小的比较稳健的统计量代替易受影响统计量。在实际能力验证结果评价时，一般采用中位值代替平均值，用标准四分位数间距代替标准偏差等[6]。

四分位数定义为1/4位置处的数值。四分位数间距IQR定义为高四分位数值和低四分位数值之差，比标准偏差大1.349 0倍，故定义标准四分位数间距为：

定义Z比分数为：

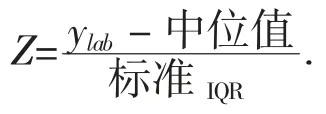
由于中位数相当于平均值，作为参考值。标准IQR相当于标准偏差，则Z比分数的最大允许值相当于包含因子k。因此对参加能力验证的实验室的Z比分数为：

|Z|≤2为满意结果，结果在95%的置信区间内；2＜|Z|＜3为可疑结果（或称有问题结果），结果出现的可能性小于5%，概率较小，故可疑；|Z|≥3为离群结果（或称不满意结果），结果出现的可能小于1%，一般不会发生，如果发生，则说明离群。

5 结语

通过以上实例，检测人员可以了解认识，面对日常检测工作产生的大量数据，如何应用数理统计与数据分析方法进行统计分析，获取可以指导生产实际的有用信息：①数据的基本统计量，如均值（x）、极差（R）、标准偏差（S）；频数分布和正态分布函数；假设检验，异常值的检验等可以了解到抽检样品的质量稳定性和符合性。②方差分析和回归分析等方法可以确定检测试验结果的影响因素。③科学的试验设计，可以有效地减少试验次数，短时间内得到预期的试验效果，进而优化试验方案，从而指导产品维护、提质和产品开发。④稳健统计方法可以相对客观地评价参加能力验证实验室的试验结果，在所有试验参与者中所处的水平。

列举了卷烟产品检测中，试验数据处理的常用的数理统计与数据方法。应用的关键为要掌握方法的原理，及其分析处理的类型，在解决实际碰到的问题时能够迅速地判断所需的方法。其他数据统计、分析处理方法，如多元统计分析、化学计量学等，虽然原理相对复杂，但随着各种统计商业软件的开发与应用，要实现各种方法相应的功能已不是难事。常用的数据分析软件有SPSS，SAS，Design-Expert，Matlab，Origin，以及最常用的Excel等，只要熟练掌握其中1～2种软件的使用方法，相信完全可以满足日常检测数据分析处理需求。