一种硅油均匀液滴喷射过程的数值模拟与实验研究

朱锦新 柴宝华 薛松龄 王泽鸣

(中国原子能科学研究院，北京 102413)

0 引言

随着人类探索空间，飞向深空，百千瓦级乃至兆瓦级的空间核反应堆电源开始展露较为广阔的应用前景。 但超大功率的空间核反应堆电源意味着更高的废热排放。 若使用传统的热管辐射器，其较大的质量与体积会给航天器的发射带来很大困难。

俄罗斯Keldysh 中心主任科罗捷耶夫提出兆瓦级核动力飞船可以采用全新的无壳液滴辐射冷却器。 该辐射器工作原理为：液态工质吸收热量后，于液滴发生器受到激励后，以一定的振荡频率从微孔阵向外喷射形成液滴层，通过巨大的总辐射面积向空间辐射热量，最后被液滴收集器收集后重新循环吸热[1]。

由于其工作原理，液滴辐射器无须携带大量辐射用翅片，展开前占用体积小，不易受微流星体动力撞击损害[2，3]，且具有很高的单位质量热辐射量[4]，在大功率空间核电源中尤为适用。

液滴辐射器系统的技术关键是液滴发生器[1]。 液滴发生器负责生成粒径均匀可控的液滴，这涉及射流破裂的相关理论。 Rayleigh 就对毛细射流在外界扰动下的崩解进行了透彻的分析[5]。 Weber 在考虑了环境介质和液体黏性后对Rayleigh 的理论进行了改进[6]。

美日俄等航天研究机构已经对液滴发生器做了相当多的研究工作。 刘易斯研究中心的工作指出，其研究的生成均匀液滴的许多可能的技术中，最合适的便是通过外加周期性扰动使射流破碎[7]。 由外加振动所致的射流破碎， 相邻液滴之间可能伴随卫星液滴。Orme 等的研究表明， 振幅调制的正弦扰动可以很好地消除次生液滴[8，9]。 Hosokawa 等使用 DC704 在真空中形成液滴流，并研究了其特性[10]。 Totani 等人通过实验探究了微重力条件下发生器生成液滴流的参数范围[11]。 俄罗斯Kedysh 研究中心实验发现，当工作液体所受扰动与它自发碎裂频率相同时， 生成的液滴流很稳定。 在2000 年，“和平”号空间站的航天员对Keldysh 研究中心研制的液滴辐射器模型进行了空间实验[12]。

国内涉及液滴辐射器的液滴发生器研究较少，徐云飞等发展液滴发生器工作过程的动力学特性计算模型，研究了喷孔位置对液滴发生器均匀液滴生成稳定性的影响[13]，徐云飞等还建立了一个考虑液滴发生器的动态特性的组合动力学模型，并通过真空环境的实验进行了验证[14]。

本文利用FLUENT 软件在实际实验装置的基础上，对DC704 工质形成的射流在不同频率正弦振动下破碎生成液滴的过程进行模拟， 并与实验结果对照。结果表明模拟结果可靠，可以减少实验量，降低成本，对液滴发生器的优化设计有理论参考价值。

1 实验装置

1.1 工质

为了减少液滴发生器的工质在空间飞行过程中的损失，其蒸气压不应超过10-9mmHg[15]。 考虑到在室温下实验，实验选择一种硅油DC704 作为工质。 其参数如表1 所示。

表1 dc704 扩散泵油相关参数

1.2 实验装置

实验装置如图1 所示，主要由发生器，加压装置与储液罐，信号发生器与放大器，以及收集装置组成。实验开始后，通过氩气瓶向储液罐中加压，使得储液罐中的工质经管道流入发生器并喷出。 接着利用信号发生器及放大器，将信号直接施加给置于发生器内的压电陶瓷，使其振动。 工质在发生器筒体内受扰动后，根据受到的扰动不同， 将发生不同的射流破碎现象，最后通过高速相机对现象进行记录研究。

发生器筒体具体相关尺寸见图2 与表2 所示。

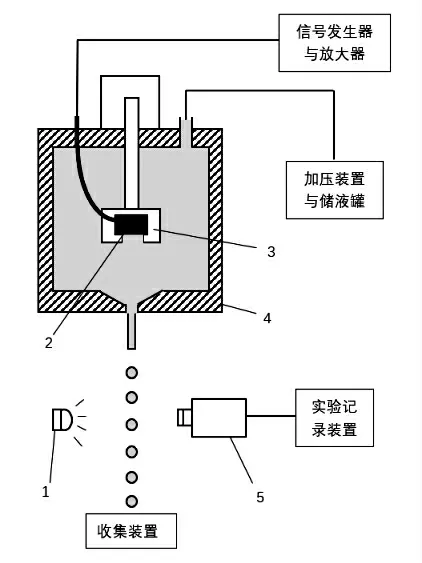
图1 实验装置示意图

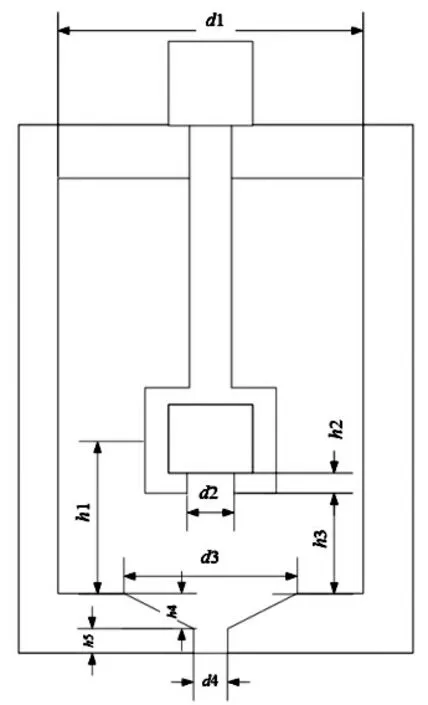
图2 相关尺寸标注图

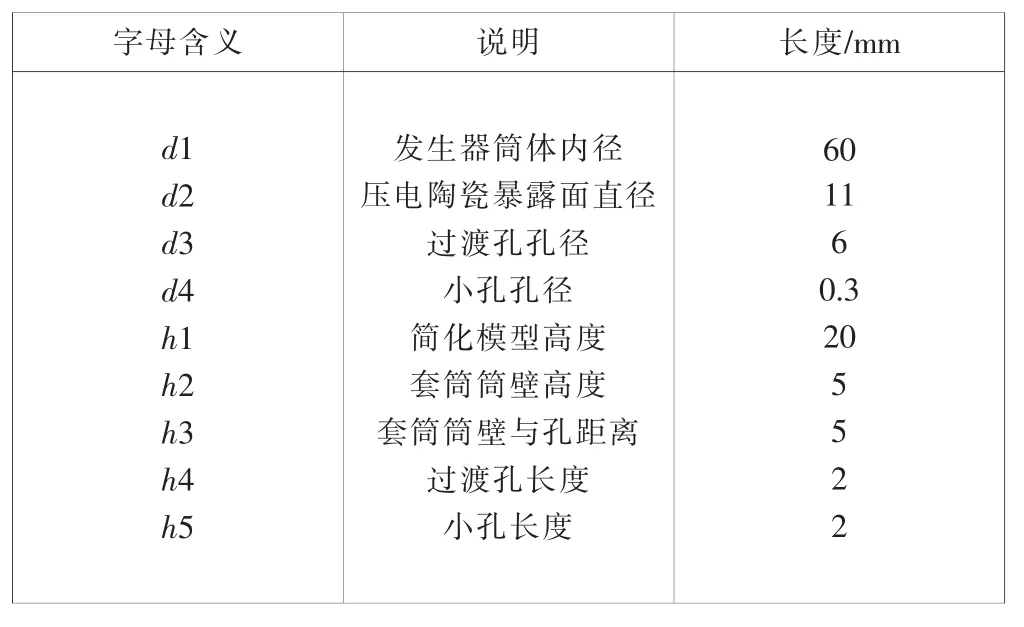
表2 尺寸说明

2 建模

将要模拟的区域包括发生器筒体内流体、孔口以及孔以下120 mm 范围内的空气环境。 由于在模拟过程中，流体始终沿轴对称分布，故通过二维轴对称方法对问题进行简化求解。 因为上筒体内流体对结果影响不大，在模型建立过程中将上筒体部分省略，最终的简化模型如图3 所示。

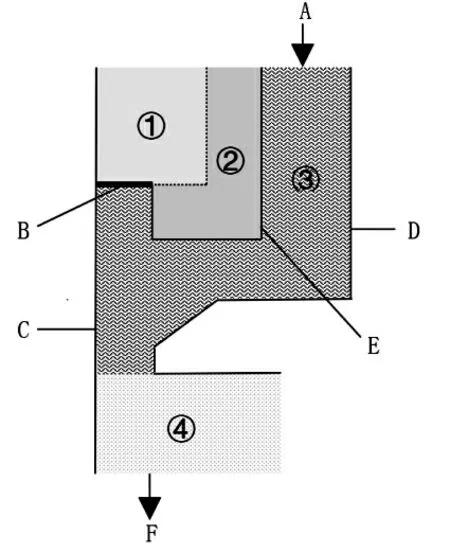
图3 简化模型与边界条件示意图

各边界条件的设置同样见图3 所示。 由于实验装置的压力计位于进液管处，建模入口位置的压力实际未知。 为保证模拟的可靠性，通过称重法，十分钟内在稳定压力下收集到工质196.3 g，以此作为质量流量入口条件的设置参数，利用FLUENT 试算，倒推得到压力入口处压力应为0.153 MPa。 本文以此作为压力入口条件的压力数值。

压力出口处设置压强为零。 根据实验条件选择参考压强。 振动面属于动网格，刚体位移，壁面1 和壁面2 设置为标准壁面条件。

进行网格独立性检验，使用射流断裂长度作为判断网格独立性的检验条件。 将不同数量的网格，在相同的条件下，于射流喷出一段时间后的同一时刻引入振动。 为避免网格数量增加后计算不稳定，统一使用1×10-6s 作为时间步长计算，并于同一时刻停止，最终结果如表3 所示。

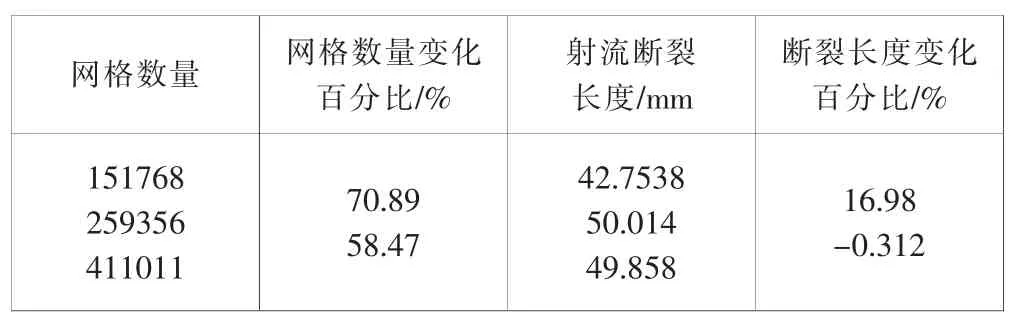
表3 网格独立性检验结果

从表3 可以看到，411 011 的网格量与 259 356的网格量相比，网格数量增加了近60%，而计算结果只有0.3%左右的差距， 基本可以忽略。 因此， 选择259 356 的网格数量作为模拟用的网格标准。

网格利用ANSYS 自带的ICEMCFD 前处理软件画出，除过渡区域使用三角形网格外，其余均为四边形网格。 实际计算时发现过渡处仍不够稳定，故利用FLUENT 自带的网格光顺功能提高了网格质量， 画出的网格如图4 所示。

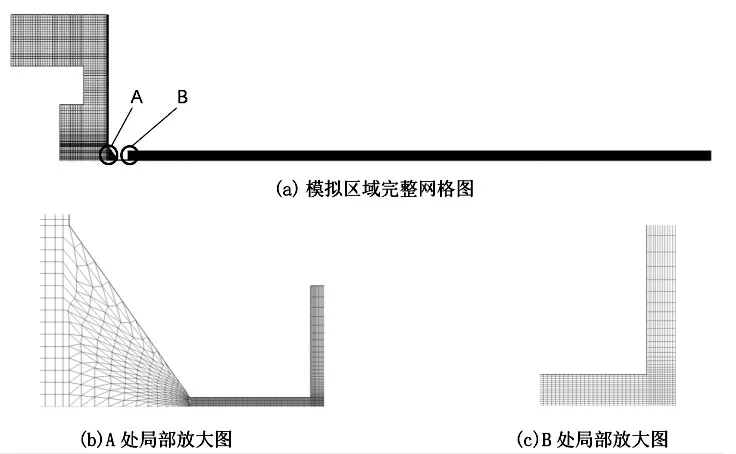
图4 实际网格图

3 扰动增长率计算

射流经受扰动之后，其表面的初始扰动会随着射流的不断发展而增长，最终使射流破碎成液滴。 通过计算增长率， 可以预测射流断裂随着扰动频率变化而变化的结果。Rayleigh 对毛细射流的断裂进行透彻分析后提出，施加于毛细射流表面的扰动按r（t）-r0=±ε（t）r0exp （βt）增长，其中 ε（t）是施加在射流上的初始扰动，r（t）是随时间变化的射流半径，r0为射流的初始半径。

在忽略重力及黏度后，Rayleigh 推导出的射流扰动增长率与无量纲波数k 的关系为：

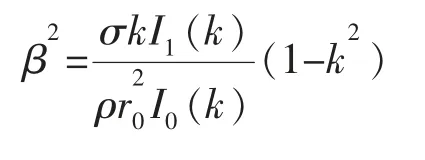
Weber 考虑了液体黏度以及环境影响后，对Rayleigh 的理论进行完善， 得出新的扰动增长率方程为：

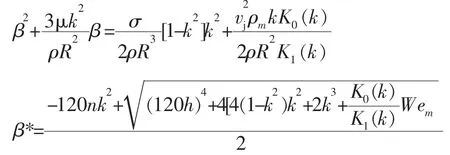
实验中通过称重法得到10 min 喷出的DC704工质总重为196.3 g。 由此可以得出小孔出口的工质流速。 但射流喷出后会发生一定程度颈缩，颈缩率难以通过理论计算得到。 本文利用FLUENT，模拟计算得颈缩率约为0.95， 在此基础上计算得射流流速约为4.73 m/s。

根据Weber 的理论，可以计算得出无量纲增长率β*与无量纲波数的关系如图5 所示。

图5 正常大气压条件下β*-k 曲线图

可以看出，β*增长率随波数k 的增长， 先增加后减小，最大增长率对应的波数为0.5106，即2 681 Hz左右。 这说明射流遭受不同扰动频率扰动时，在合适范围内，其断裂长度随频率的增加，应当呈先减小后增加的趋势，并在2 680 Hz 附近达到最小值。

4 数值计算结果

4.1 模拟设置

选择FLUENT 求解器求解控制方程组。 根据之前得到的质量流量可知流速，计算后得出口雷诺数约为36.4。 一般认为从狭缝或孔中射出的射流的临界雷诺数为30[16]，因此实验射流属于紊流。 但在FLUENT中，湍流模型更适合模拟大雷诺数条件，而本问题的雷诺数超出界限较少，模拟区域也并不大，故使用层流模型对整个实验过程进行模拟。

使用流体体积函数(VOF)模型求解，利用PISO 算法进行压力—速度耦合离散，PRESTO！ 算法进行压力离散，second order upwind 算法进行对流项离散。

空气区域使用FLUENT 默认的空气参数。 本文使用fluent 的动网格功能，将振动面视为刚体运动变形。时间步长取4×10-6s，于射流喷出0.03 s 后引入振动，到0.056 s 时停止计算。 参考压强设置为101 325 Pa，此时入口压强为254 325 Pa，出口压强为101 325 Pa。将引入的扰动振幅设置为2×10-7m。

4.2 数值计算结果

未施加振动时，模拟结果如图6 所示。 图6（a）为空气区域长120 mm 的情况，可以看到，模拟结果从孔口一直到120 mm 的范围的尽头，射流始终未断裂。最后将空气区域延长至160 mm，如图6（b），可以看出，射流在距孔口155 mm 处发生断裂。

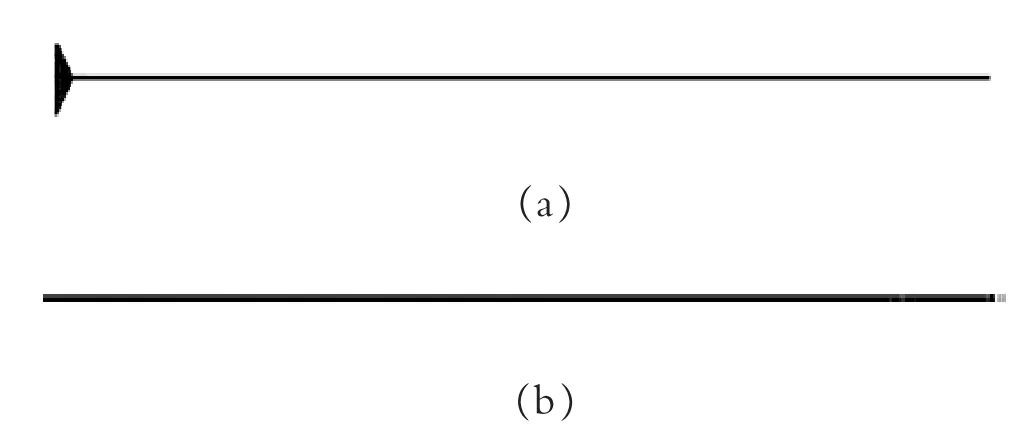
图6 未施加振动时，射流的模拟图

引入不同频率正弦振动的单孔射流破碎模拟结果如图7 所示。 可以看到，随着频率的增加，射流断裂长度先减小后增加。 与Weber 理论计算得出的结果基本符合。 以最后11 个液滴间的10 个间距值与它们的平均值作比较。 3 000 Hz 到1 400 Hz 之间的模拟结果，各个间距值与平均间距值的百分比偏差值都在百分之十以内，1 000 Hz 时， 最后成型的液滴不足11个，但是各个成型液滴间距值与平均间距值的百分比偏差值仍在百分之十以内的，可以认为此时液滴都是均匀的。 而低于600 Hz 时，射流断裂长度较长，且液滴不均匀。 高于3 800 Hz 时，发生液滴碰撞。

图7 施加正弦振动条件下射流破碎模拟结果

5 实验结果

高速相机拍摄的部分实验结果如图8，9，10 所示。 图8 实验结果为未施加振动时的射流图像。 可以看出，尽管未施加振动，射流依旧在距孔口86 mm 处发生了断裂，且生成的液滴不均匀。 而图6 的模拟结果显示，射流直到距孔口155 mm 处才发生断裂。推测是实验条件下，孔口边缘存在毛刺，且孔内壁粗糙，因此射流在喷出有更大的初始扰动。 而模拟中，孔口为完全的理想圆孔。 而实际实验装置中，进液管，压电陶瓷线路，连杆等，也会对实验造成一定影响，模拟中将这些部分都忽略了，因此产生了结果差别。

如图9 所示， 可以看出， 施加600 Hz 正弦振动后， 射流断裂长度明显缩短， 但生成的液滴并不均匀，且出现液滴碰撞。 图6 与图7 显示，施加600 Hz正弦振动后，模拟的射流断裂长度由155 mm 缩短到120 mm 附近。 模拟结果与实验结果趋势一致。

处于中间频率范围的部分结果如图10 所示，可以看到，实验与模拟符合的很好，最优频率约在2 600 Hz处， 射流断裂长度在最优频率处最短， 越偏离最优频率，射流断裂长度越长。 实验图像也能观察到1 000 Hz到3 000 Hz 生成的液滴大小与间距均匀。

图11 为施加3 200 Hz 正弦扰动条件下模拟与实验的结果对比，可以看出，虽然模拟结果中的液滴比较均匀，但实验中生成的液滴间距并不均匀。 图12 为3 400 Hz 时模拟与实验的结果对比。 可以看到，模拟结果放大后，尽管能观察到液滴间距并不均匀。 放大图像中的所有间距与平均间距值的最大百分比偏差也仅为41.564%。 而实验图像中液滴的不均匀度明显更高，甚至出现了液滴碰撞融合。 而模拟结果中直到3 800 Hz 才发生液滴碰撞。

图8 未施加振动时，实验图像

图9 施加600 Hz 正弦振动时，射流破碎图

图10 施加正弦振动条件下部分实验结果

图11 施加3 200 Hz 正弦振动时，模拟与实验结果

图12 施加3 400 Hz 正弦振动时，模拟与实验结果

经过以上对比，可以看出，模拟结果更偏理想化。在生成均匀液滴的频率范围外，模拟结果不是特别准确。但即使结果有所区别，发展趋势是一致的。而生成均匀液滴的频率范围内， 模拟与实验结果符合得很好。 说明本文的模拟方案可行。

6 结论

（1）施加不同频率振动时，射流断裂长度先减小后增加，越靠近最佳频率，射流断裂长度越长。 使用DC704 作为工质时， 在一个比较宽的频率范围内，射流断裂生成的液滴都很均匀。

（2）模拟结果与实验基本相符，证明了本文模拟方案的可靠性。

（3）本文模拟结果可以为液滴发生器实验提供参考数据，降低实验量，为相关设计提供理论参照。