基于深度卷积神经网络的非线性模型修正方法

邓忠民，张鑫杰

(北京航空航天大学 宇航学院，北京 100191)

0 引言

近年来，有限元模型修正逐渐得到国内外研究者的广泛关注[1-3]，其发展方向逐渐从线性扩展到非线性。非线性模型修正包括两方面[4]：1)非线性的描述及量化[5]，即如何衡量结构真实响应和仿真预测结果之间的差异；2)如何对待修正的非线性参数进行识别和更新[6]。常见的几类传统非线性模型修正方法包括：误差法[7]、三段法[8]、神经网络法等[9]。这些传统的人工非线性特征提取的过程中，首先需要对非线性成分进行识别和定位[10]，然后利用信号处理方法对非线性信号进行特征提取，将识别出的非线性成分作为修正目标[11]，进而求解出待修正参数的预测结果。在这一过程中由于非线性特征通常较为复杂，人工非线性提取和量化方法存在着一定的误差[12]。随着特征提取技术的不断发展，人工特征提取的局限性也日益显现[13]。

而深度学习理论对于这种复杂信息的特征提取有着传统人工特征提取方法难以比拟的准确度和特征维度[14]，被广泛应用于影音图像领域的识别[15]、分类、回归等问题。深度卷积神经网络(DCNN)的出现减少了大量人工特征设计[16]、选择和提取工程，可以完成更为自动化的特征分析过程[17]。与传统人工神经网络不同，深度卷积神经网络不需要严格选择特征[18]，只需要引导学习来达到期望的目标[19]。本方法利用深度卷积神经网络替代传统方法中的非线性特征识别过程，通过非线性激活函数，完成非线性的逆向传递关系，提高非线性问题的表征能力。与传统的方法相比，这种方法能够有效减小非线性成分分析和提取中产生的误差，可以减小由于认知不足导致的非线性识别精度不足和量化准则不合理造成的精度误差，对数据处理方法的依赖程度较低，具有更广泛的适用性。

1 传统方法修正流程

对于一个多自由度的非线性结构，有如下的动力学微分方程：

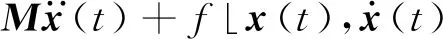
(1)

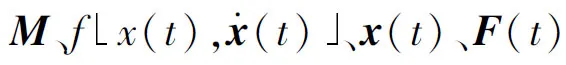
(2)

式中Kc表示非线性刚度系数，用于描述非线性恢复力。通常Kc可用如下表达式求解：

Kc=c·K

(3)

其中：c为非线性系数；K为结构的刚度矩阵。

传统方法中最重要的两部分就是非线性识别和目标函数的构建。传统方法中主要构建了如下所示的求解目标：

θupdated=argminRc(θ)

(4)

式中Rc(θ)为真实结构响应与模型预测结构响应之间的差距函数，为最小化寻优的目标函数；θupdated即为最终参数修正后的结果。Rc(θ)的表达式为

(5)

其中Gresidual为非线性响应的特征提取函数，用于构建响应实验测量的真实结构非线性响应和仿真模型非线性响应之间的差距函数。

2 方法介绍

2.1 方法流程

本文主要的方法流程如下：

1) 数据预处理。利用初始有限元模型获得仿真样本，将模型的时域响应数据处理成时频图或不确定性响应图像。

2) 构建训练网络。设计网络结构，选择合理的非线性激活函数，设计损失函数，利用步骤1)中处理后的数据完成网络训练。

3) 将实验测量的真实结构响应按照步骤1)处理成时频图或不确定性响应图像，输入训练好的网络中，网络的输出即为待修正参数的预测结果。

2.2 数据预处理

本文采用深度卷积神经网络进行自动化非线性特征提取，其确定性修正输入为结构的时频响应图，不确定性修正输入为不确定性加速度时域响应。

在确定性算例中，本文采用短时傅里叶变换(short-time Fourier transform，STFT)来替代普通的傅里叶变换，实现时频转换。其示意图如图1所示。从图中可以看出，当对时频图进行特征提取时，卷积核滑过时频图的时域和频域维度，对局部响应特征进行提取。随着网络层数的不断增加，能够提取到的特征信息维度越来越高，证明本方法能够提取到更为丰富的非线性信息。求解算法对于真实传递过程的表征能力较强。

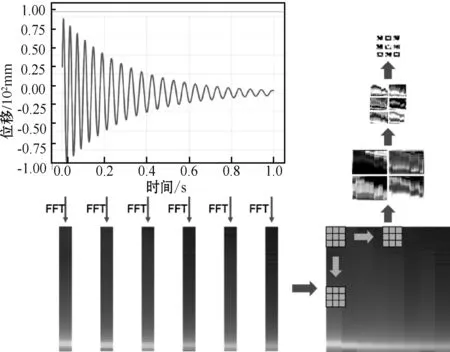
图1 时频图转化及特征提取示例

2.3 激活函数的必要性

在卷积神经网络中，特征提取过程及参数传递过程中卷积、池化及全连接操作均为线性链接，如果只有这些结构，那么网络只能将输入进行线性组合再进行输出，只能完成线性传递关系的表征。

如果不采用非线性激活函数或采用线性激活函数，网络隐藏层输出为：

z(1)=fl(a(1))

(6)

z(2)=fl(a(2))

(7)

式中fl为激活函数，其表达式如下：

(8)

式中wl为线性激活函数。以线性激活函数为例：

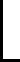
(9)

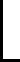
(10)

进而得出：

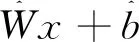
(11)

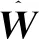
本文采用ReLU函数作为非线性激活函数。ReLU函数及其导数的表达式如下：

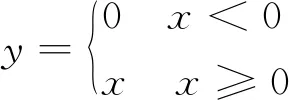
(12)

其在x∈[-5，5]内的函数图像如图2所示。

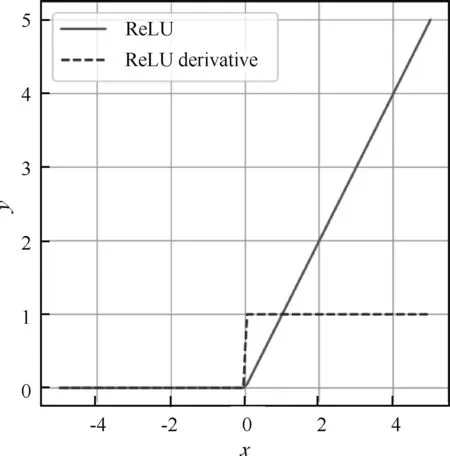
图2 ReLU 函数示意图

ReLU函数能够快速收敛，还能有效缓解梯度消失的问题，同时能够给神经网络提供稀疏表达能力。并且，ReLU函数计算过程中仅需要一个门限值，其计算速度明显快于Sigmoid函数和tanh函数等非线性激活函数。

3 算例1

3.1 算例描述

本算例采用了文献[20]中的非线性振动模型算例。其系统方程为

(13)

利用多尺度法可以求解出结构的时域响应一阶近似解的表达式为

(14)

式中：a0和β0分别为初始振幅和初始相位，取值分别为100 mm和0；识别时间段为0～1 s；待修正参数为ω0、δ和ε。

本文中，将文献[20]中的非线性参数识别方法命名为M1方法，将本文提出的基于深度卷积神经网络的方法命名为Nnet。M1法利用小波变换对非线性时域响应进行分析，为解决边端效应又采用BP神经网络对非线性模型参数进行预测延拓。Nnet法利用结构的时域响应，对待修正参数的数值进行预测求解。首先，生成训练样本配对，将时域响应通过STFT转化为频谱图。然后利用训练数据对网络进行训练，最终将真实的响应频谱图输入训练好的网络，即可得到参数修正结果。

3.2 修正结果

本文对两种方法的非线性参数识别结果进行了比较，结果如表1所示。

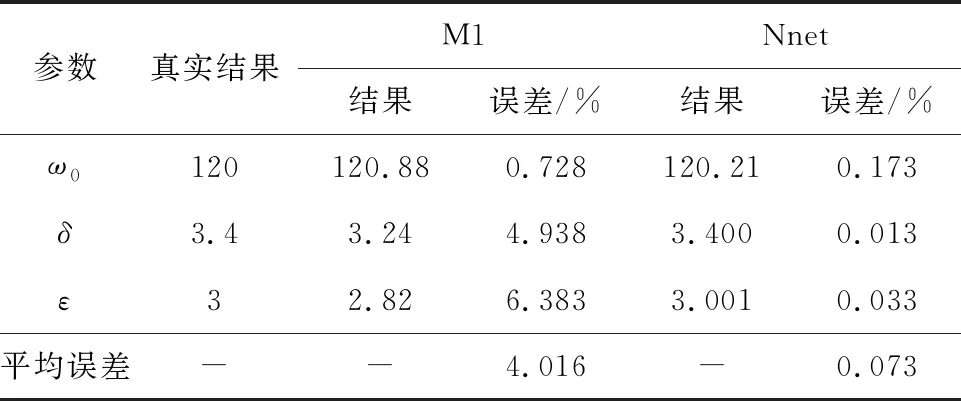
表1 非线性参数识别结果

从表中可知，两种方法求解的ω0误差均小于1%，而M1方法求解的δ和ε误差较大，Nnet方法求解出的结果误差均小于0.1%。文献方法求解出的参数平均误差约为4.02%，而本文提出的方法求解的参数平均误差为0.07%，与文献方法相比有明显提升。证明本方法的参数修正精度更高，更接近真实参数值。

将修正后的非线性参数代入结构的振动方程中，可以求解出修正后模型的响应预测结果。如图3所示为修正后的结构时频图对比，可以看出结构的时频响应图谱特征非常隐晦，通过人工特征提取的方法很难对其进行很好地分析。如果特征设计过于简单，将会导致大量的隐藏特征信息丧失，造成精度下降。因此，利用深度卷积神经网络进行特征提取能够有效避免特征设计不合理带来的误差，提高对于复杂特征分析的准确度。通过观察图3可以看出，在0.6～0.8 s内，400～500 Hz部分的频谱图中，Nnet的修正结果与真实结果更为吻合。

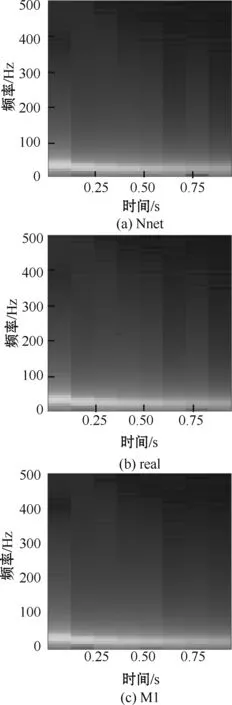
图3 修正后模型时频图

如图4所示为时域位移响应曲线。从图中可以看出，Nnet修正后的模型响应振幅与真实的时域响应相比更为接近，证明修正后的模型更加接近实际结构。同时，可以发现，虽然M1方法求解的δ和ε误差较大，但其修正后结果的时域响应与实际结构的时域响应差别仍在可接受范围内。说明δ和ε的变化对结构响应的影响能力有限，灵敏度较小，而ω0的变化对结构响应影响较大。

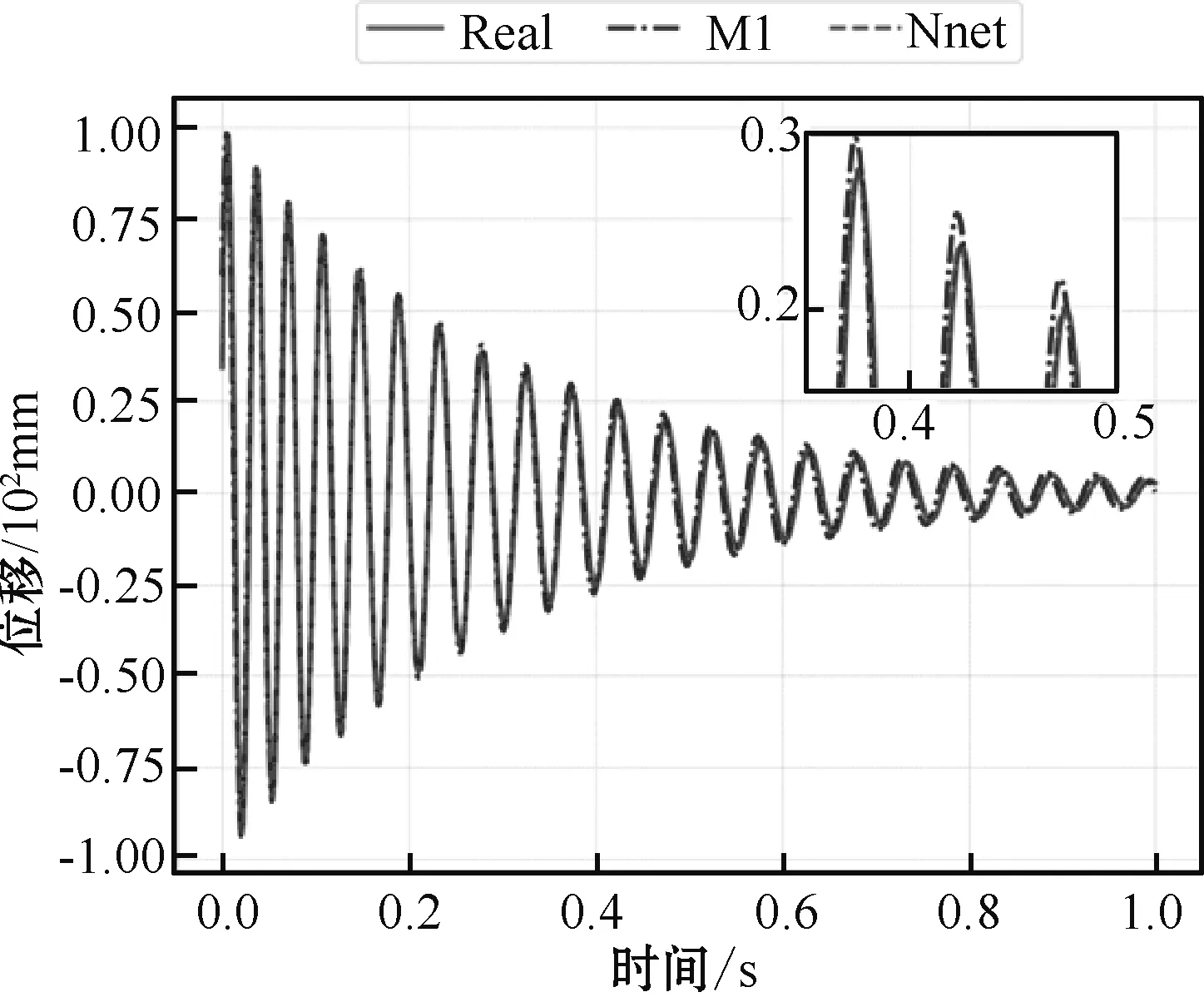
图4 修正后模型位移时域响应

为了进一步证明修正后模型的精度，本文还利用训练数据外的系统瞬时振幅对修正后的模型进行确认，如图5所示。可以看出，Nnet修正后的模型瞬时振幅与实际结构的吻合度很高，这进一步证明了方法的优越性。

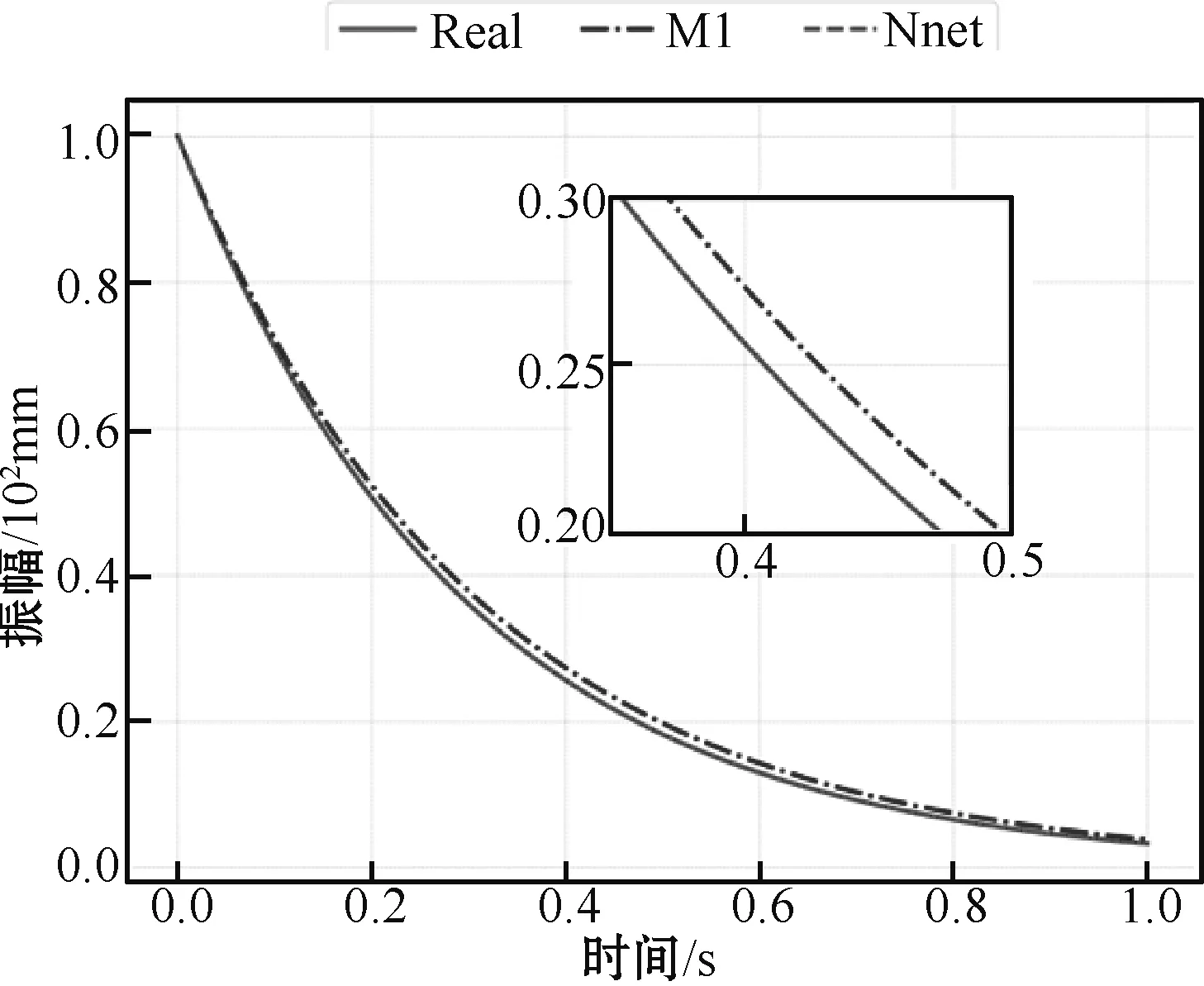
图5 修正后模型瞬时振幅

4 算例2

4.1 算例描述

不确定性算例采用文献[21]中的双层钢架结构进行验证，如图6所示。该结构中的竖直支柱杆件只有弯曲刚度，并无质量。水平杆有质量和水平方向位移。水平杆质量m1=3.7 kg，m2=1.5 kg，不确定性参数为K1和K2，其运动微分方程如下：

(15)

其中

Kc=c·K·104

(16)

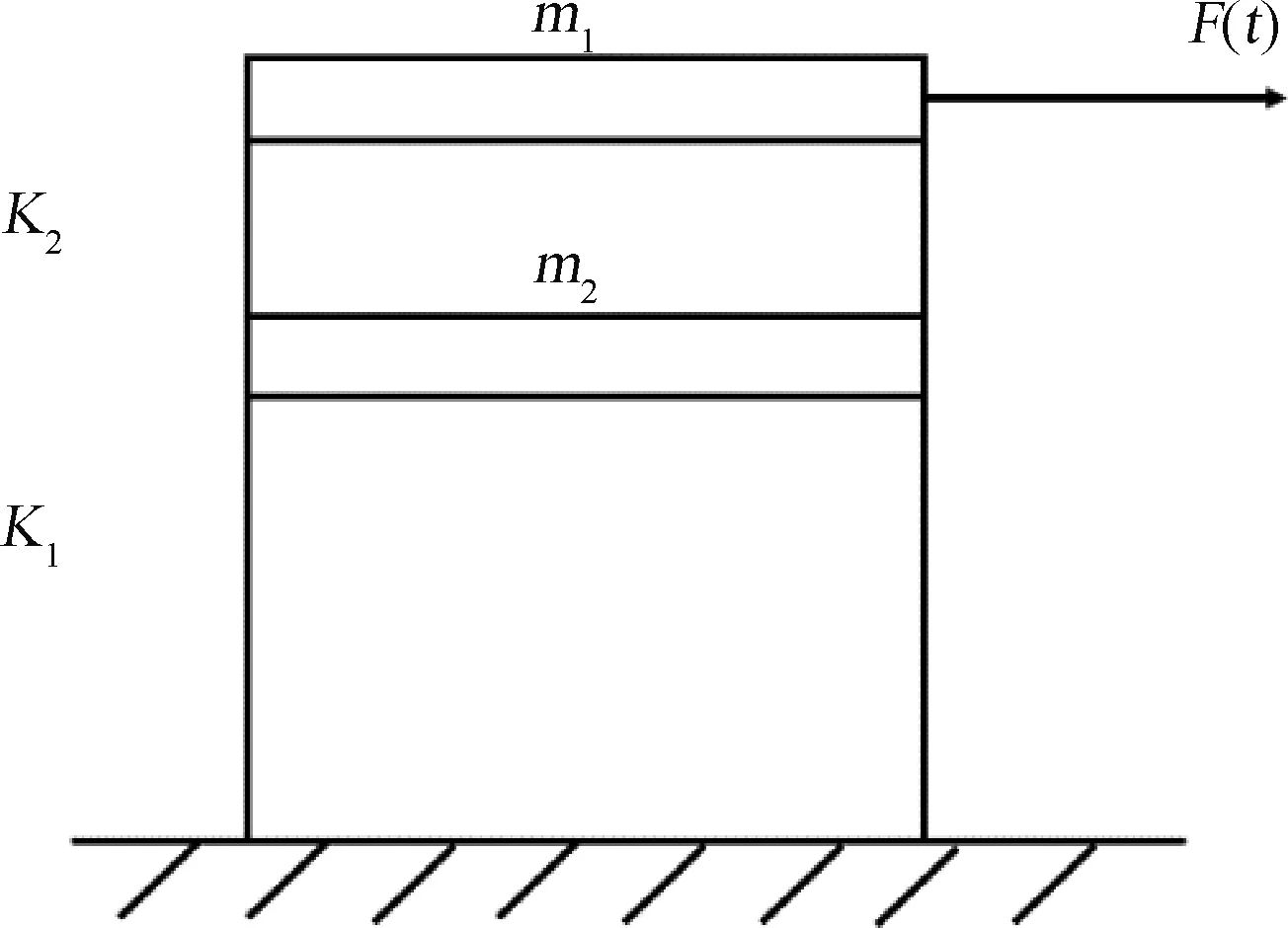
图6 钢架结构

本文中，模型修正的目标为结构的位移时域响应数据。将不确定性的位移时域响应数据按图7所示的方法进行序列化排序，后转化为响应图像后，输入设计好的Nnet网络中进行训练。

图7 不确定性非线性响应预处理

4.2 修正结果

训练过程中的参数分布结果如图8所示。可以看出，随着训练的进行，参数的分布预测值越来越接近于真实结果，最终收敛于真实参数分布附近。因此，将200代左右的训练结果作为最终训练完成的网络，将真实结构的不确定性数据输入到训练好的网络中，则可以得到修正后的参数分布结果和概率密度估计结果，如图9和图10所示。由参数分布散点图可知，本方法能够对不确定性参数的分布状态进行直接预估，而且与实际参数分布非常接近。从参数的概率密度估计也可以看出修正后的概率分布结果与真实结构吻合度较高。为了方便说明，本文还统计了修正参数的分布均值和方差，二者的修正误差结果如表2所示。从表中可以看出，Nnet方法修正后的结构参数与真实结构参数的均值和方差均小于1%，证明该方法有较好的修正效果。

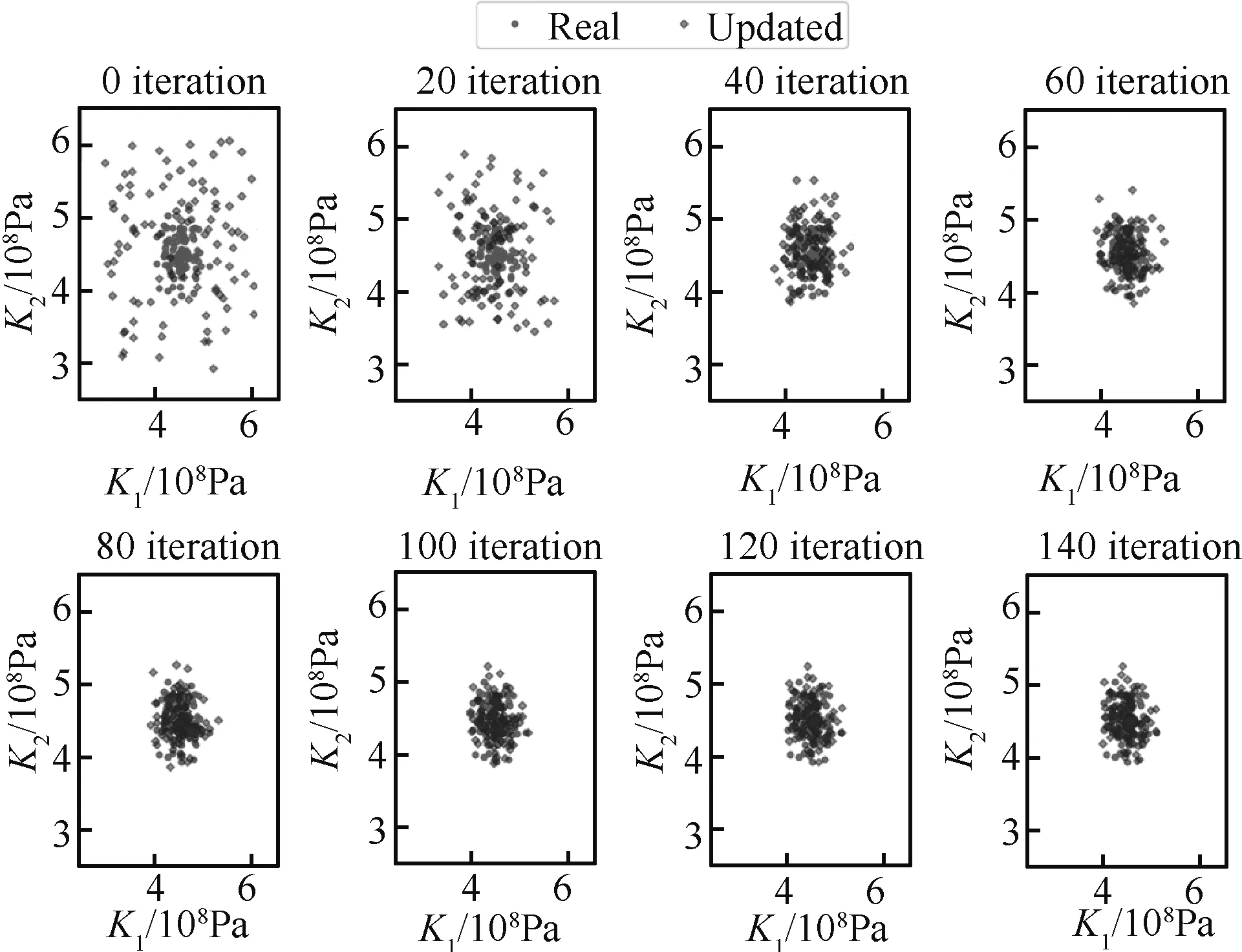
图8 迭代收敛过程

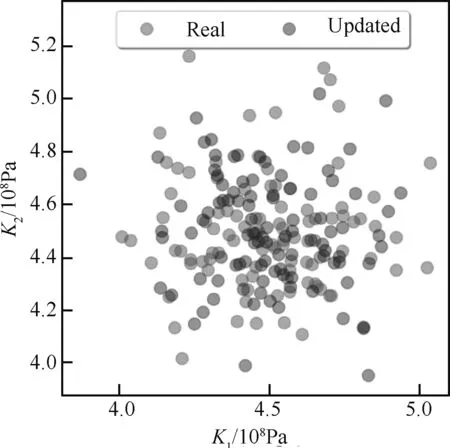
图9 修正后参数分布

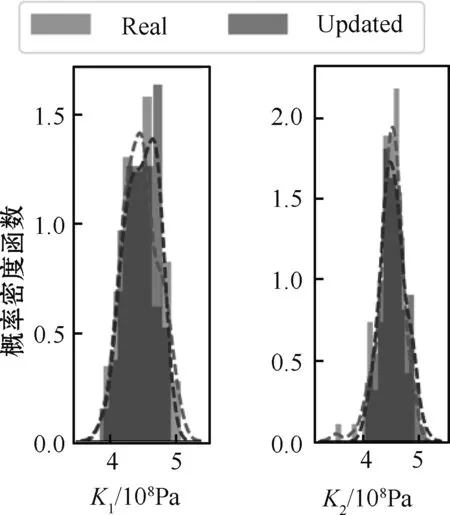
图10 参数概率密度估计

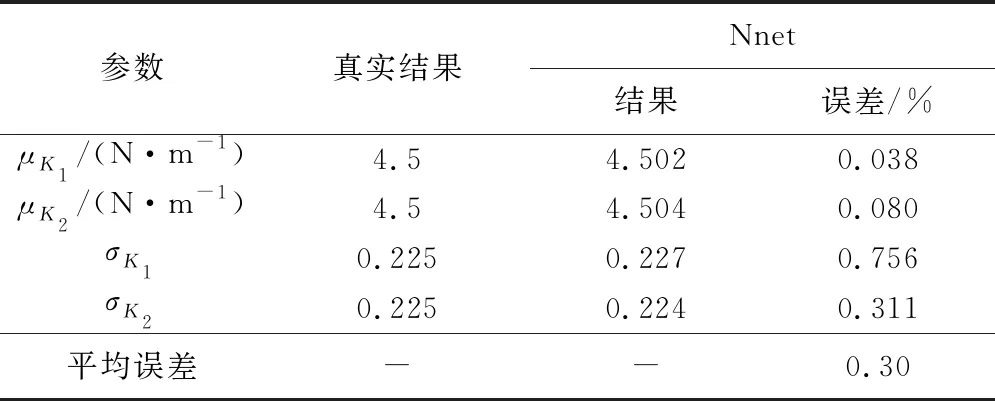
表2 不确定性参数修正结果

除了观察参数修正结果本身，还需要对修正后模型的响应预测进行评估分析。因此将修正后的不确定参数分布样本逐一输入到待修正模型中，依次得到对应的不确定性响应分析结果。为了方便观察，图11中展示了0～1 s内每个时间点上不确定性响应的均值，可以看出修正后模型的响应预测均值与真实结构的响应均值吻合度较高，证明修正后模型响应分布的中心与实验测量结果的重合度较高。计算实验测量响应均值与模型预测响应均值的FRAC值为0.999 8，进一步证明了均值预估精度较高。

图11 修正后模型0～1 s位移响应均值

图12中展示了响应分布的上下界，响应上下界可以反映出响应的变化范围。由图可知，0～0.5 s内修正模型的不确定性响应分布范围与真实结构的分布范围非常接近，曲线重合度较高。而0.5～1 s范围内的分布结果有少量偏差。为了验证其准确性，计算实验测量响应上界与模型预测响应上界之间的FRAC值为0.993 4，响应下界的FRAC值为0.982 6，在可接受的精度范围内。这说明在0～1 s内，修正后模型的响应预测结果与实验测量结果的分布情况重合度较高。证明在修正数据范围内的模型响应计算结果能够对真实结构的响应结果进行预测，修正后的模型能够较准确地表征。

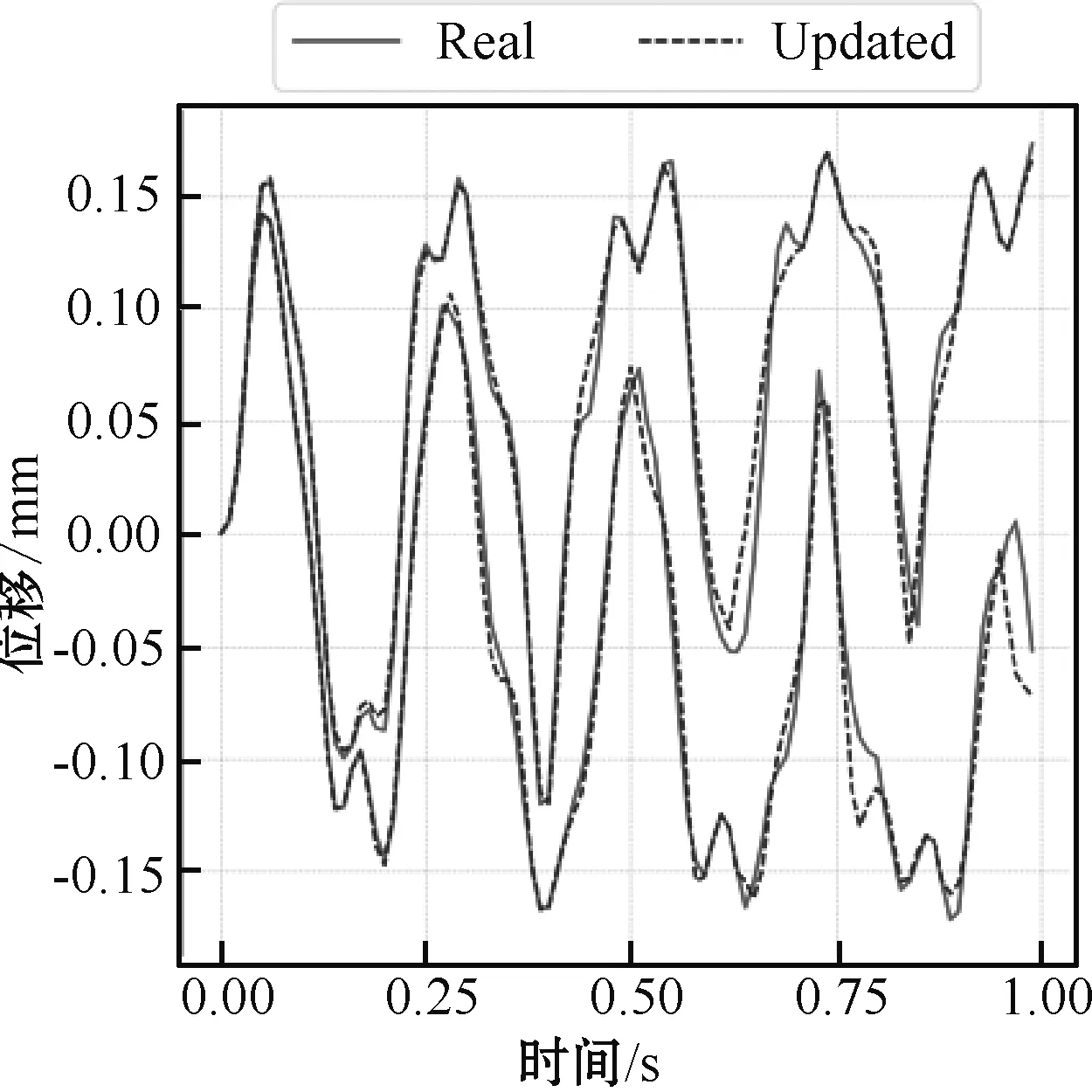
图12 修正后模型0～1 s位移响应上下界

5 结束语

本文提出了基于深度学习的非线性结构模型修正方法，分别对确定性问题和不确定性问题进行了研究。通过与传统非线性修正方法相比，可以看出本方法能够完成对于结构时频响应的自动化特征分析和提取，减少了人工非线性特征识别、量化以及误差目标函数构建过程中造成的精度损失。通过卷积神经网络，可以构建一个由结构时频数据到待修正参数的高精度非线性逆向映射，利用网络前传即可获得参数修正结果。修正结果证明，基于深度卷积神经网络的非线性模型修正方法能够获得更高的参数修正精度，修正后模型的响应预测结果和真实结构的实验测量响应更为接近，修正后模型更加接近于真实结构。