锂电池SOC 估算方法的研究*（续1）

孙正 李军

（重庆交通大学机电与车辆工程学院）

锂电池在各类动力电池中，具有比能量高、充电快、使用寿命长、以及对环境“友好”等优点，已经广泛应用于电动汽车中。电池的荷电状态（State of charge，SOC）估算作为电动汽车电池管理系统（Battery management system，BMS）的核心技术，其估算的精度的提高，对延长电池的使用寿命、优化能量管理有着重要的作用[1]。由于在实际的估算过程中，锂电池的SOC 不能直接进行观测，只能通过其内部参数与SOC 的关系获得，但锂电池又是一个多参数影响的、复杂的非线性系统，所以SOC 的估算有一定的难度。传统估算方法有安时积分法、开路电压法、卡尔曼滤波算法等，但单一方法的精度较差，不适用于实际工况下进行快速估算。为此，现阶段为了提高SOC 估算的精度，很多学者展开了研究，主要是在传统方法的基础上结合各类优化算法来达到目的，通过仿真的验证，其最大估算误差能够达到4%以下，已经具有了较好的估算精度和鲁棒性。基于上述背景，文章分别从影响SOC 估算精度的电池模型以及参数辨识等问题展开分析，主要针对现阶段的锂电池SOC 估算方法的特点、原理等进行了归纳总结。

1 电池模型和参数辨识

1.1 SOC 估算的影响因素

影响锂电池SOC 估算的主要因素有充放电电流、温度、电池老化、自放电等：1）充放电效率。在一定试验条件下，只改变电流的倍率对电池进行充电，充放电电流大小与充放电速率成反比，即充放电电流越大，电池充放电的速率越慢[2]；2)温度。不同温度下，同一SOC 估算方法的精度会有很大差别，尤其是低温环境下，对比常温环境，电池参数会有很大变化，甚至SOC 的估算精度会大幅下降。因此温度在SOC 估算的过程中不可忽视，研究过程中需要对针对温度参数的影响对SOC 的估计值进行修正，在SOC 估算方法中设计温度权重，或设计带温度参数的电池模型；3)电池老化。电池老化后，电池的内阻会增大，总电量及充放电速率均会下降，进而影响了模型参数与SOC 建立的函数关系，导致SOC的估计值存在误差；4)自放电。电池的自放电会使电池电量流失，同样导致SOC 估算存在误差。所以，在电池模型及估算方法中需要针对以上几个主要的影响因素来建立修正系数，来保证电池SOC 的估计值有较高的精度。

1.2 电池模型

SOC 估算是通过建立近似精确的电池模型，得到模型参数与SOC 之间的关系，将复杂的非线性关系问题转化成近似线性的数学关系，再通过数学关系求解得到电池的SOC。因此，电池模型越接近真实模型，所得到的SOC 值也越精确，但电池模型的精度越高，其复杂度也会越高，导致SOC 估算的计算量过大。所以，合理选择电池模型有利于提高SOC 估算的精度和实用性。现阶段电池模型主要有电化学模型、等效电路模型、神经网络模型等。等效电路模型主要包括Rint 模型、Thevenin 模型、2 阶RC 模型、GNL 模型、PNGV 模型。文章主要介绍SOC 估算中使用较多的等效电路模型。

1)Rint 模型，如图1 所示。Rint 模型作为初始的等效电路模型，其结构简单，计算量小，但无法体现电池的动态特性，精度较低，现阶段研究中使用较少。

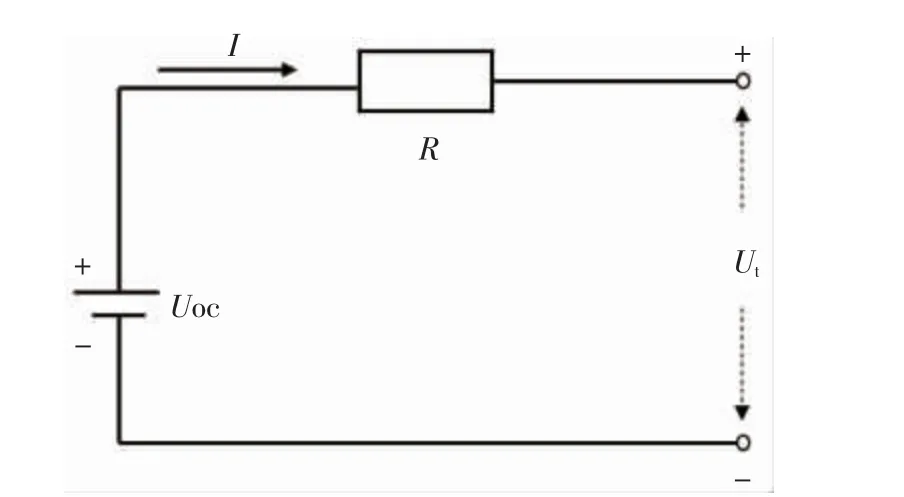
图1 Rint 模型

2）Thevenin 模型，如图2 所示。相比于Rint 模型，增加了1 个RC 电路，能够反映电池的动静态特性，且计算量较小，便于求解SOC，并有着不错的估算精度，被使用较多。

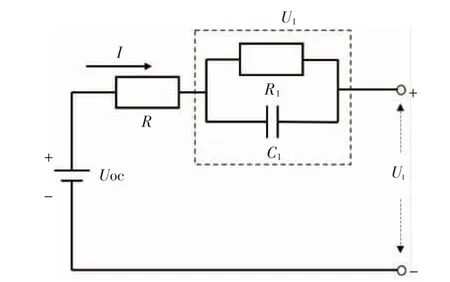
图2 Thevenin 模型

3）2 阶RC 模型，如图3 所示。2 阶RC 模型是在Thevenin 模型的基础上又增加了1 个RC 环节，相比之下，能够更精准地反映电池的动态特性，其估算精度更高，继而被广泛应用。

图3 2 阶RC 模型

以2 阶RC 模型为例，根据基尔霍夫定律和安时积分法，状态空间方程为：

式中：Qn——电池总电量；

SOC（k）——k 时刻SOC 值；

T——采样时间；

ωk——过程噪声矩阵；

υk——观测噪声矩阵。

RC 阻容环节主要是用来描述电池反应过程中的极化效应[3]，但随着RC 环节的增多，电池模型的复杂度也越高。文献[4]提出了多模模型的联合估计算法，通过对电化学阻抗谱（EIS）进行分析，利用贝叶斯定阶准则（BIC）来确定模型的阶数，合理选取1 阶或2 阶模型进行参数辨识，求解得到SOC，该方法能够减少算法的迭代次数，更快地得到SOC 的准确值，又保证了估算的精度。文献[5]提出了融合模型的方法，通过极限学习机算法，建立了适用于1 阶Thevenin 模型的SOC 误差预测模型，并将该模型的输出结果作为补偿项对等效电路模型法的SOC 估计结果进行误差校正。该方法能够减少模型的复杂度，以及测量误差，进一步提高了SOC 估算的精度。文献[6]提出了变温度模型，通过引入电阻、电容温度修正因子，建立了变温度2 阶等效电路模型。该方法提高了模型的精确度，解决了温度对SOC 估算精度的影响。

1.3 参数辨识

在SOC 的估算过程中，需要辨识的模型参数有开路电压Uoc、欧姆内阻R、极化电阻R1和极化电容C1。

通过数据，以SOC 为函数自变量，Uoc、R、R1、C1为函数，进行拟合，分别得到各函数关系式，并根据函数拟合出曲线，与精确值进行对比后，得到模型参数误差曲线，如果各参数误差较小，说明电池模型能够准确地描述各参数值，进而用于各类SOC 估算方法，求解SOC。曲线的拟合，通常选用最小二乘法来进行，最小二乘法原理简单，计算量较小，拟合函数的精确度较高。

综上，在模型复杂度不高，计算量较小的基础上，电池模型参数辨识的结果越精确，所获得SOC 的估计值也越精确。因此，优化参数辨识这一过程，对于提高电池SOC 估算精度至关重要。

为此很多学者提出了更优的在线参数辨识方法，能够实时地进行参数辨识，并结合SOC 估算方法将结果不断地迭代修正，大幅减小了估算的误差。文献[7]提出利用Hermite 插值法建立等效电路模型，并拟合各参数曲线。该方法解决了最小二乘法拟合函数时，数据不能全部落在拟合曲线上的问题，并且有较好的逼近效果和曲线的平滑度，其参数辨识的结果更加精确。文献[8]提出了带遗忘因子的递推无参数最小二乘法（PF-RLS）来实时提取更新电池参数，进行参数辨识。文献[9]提出了改进的遗传算法(IGA)框架，能够快速缩小最优解的范围，在线快速进行参数辨识，提高了SOC 估算的效率。