产流模型蓄水容量的一种尺度校正方法
李 超,黄 薇,向小华,王志伟,吴晓玲
(1.河海大学水文水资源学院,江苏 南京 210098; 2.杭州市水文水资源监测中心,浙江 杭州 310016)
与集总式模型相比,分布式水文模型能更加细致地描述降水和下垫面的空间异质性,模型参数的物理意义也更加明确,从而能降低模型对于参数率定的依赖性[1-5]。但分布式水文模型也存在尺度选择的难题,国际地学研究领域多次举办尺度专题研讨会,以深化对水文尺度问题的认识并探讨解决途径[6-7]。不同尺度的水文规律以及水文尺度间的转化关系已成为水文研究的热点问题[8-10]。在流域水文模型中,产流计算一直是水文研究的核心课题[11-12]。新安江模型采用蓄水容量面积分配曲线来考虑土壤缺水量分布不均的问题,其中流域平均蓄水容量需要通过资料率定得到[13]。当流域缺乏实测水文资料时,就无法反映下垫面空间异质性,导致模型模拟结果不佳[14]。目前,通过下垫面因子间接推求蓄水容量已有大量研究,石朋等[15]考虑到地形指数实质上反映了土壤缺水量的空间分布不均匀性,这与蓄水容量的本质一致,从而建立了蓄水容量同地形指数的定量函数关系;孔凡哲等[16]根据地形坡度对产流的影响,建立了各子流域蓄水容量同地形坡度的关系,并在淮河大坡岭流域的应用中取得较佳的模拟结果;Chen等[17]提出了基于地形指数的不易产流度指数曲线(IRDC曲线),用于代替传统新安江模型中的蓄水容量面积分布曲线;向小华等[14]以Van Genuchten模型(VG模型)表述的土壤水分特征曲线为基础,建立了融合地形和土壤特征影响的蓄水容量显式表达式,为空间尺度的产流计算和无资料区的水文模拟提供了计算方法。
高分辨率的数据会带来较大的计算量,而低分辨率的数据通过校正,可在获得接近高分辨率数据计算结果的同时大幅度减小计算量、提高计算效率,进而将分布式水文模型用于实时问题。本文以地形指数与蓄水容量之间的定量函数关系[18-19]为依托,通过引入分辨率因子和分形理论[20-21]对上游集水面积和坡度因子进行尺度校正,构建地形指数尺度校正公式,实现蓄水容量的尺度转换计算。
1 尺度校正方法
1.1 地形指数的尺度校正
地形指数由上游集水面积和坡度共同决定,单点地形指数计算公式为
(1)
式中:λi为流域内某一点的地形指数;Ai为流域内某一点的上游集水面积,m2;li为流域内某一点的等高线长度,m;βi为流域内某一点的坡度。
研究表明,DEM数据分辨率的降低会导致流域平均集水面积的增加以及地形整体坡度的减小[22-24],尺度差异越大,偏差也就越大。针对上游集水面积Ai,在较低分辨率下,可以通过引入分辨率因子校正获得较高分辨率的上游集水面积[25]:
(2)
式中:Asi为校正到目标尺度的流域内某一点上游集水面积,m2;Ai为实际尺度的流域内某一点上游集水面积,m2;Ns为实际尺度与目标尺度栅格尺寸比的平方;If为分辨率因子。
目前,坡度的尺度校正主要基于分形理论、直方图匹配和坡度图谱,本文引入分形理论[25-26]对坡度衰减现象予以纠正,期望较低分辨率下的坡度与目标高分辨率下的坡度维持统计规律的一致性,计算公式为
(3)
其中
式中:βsi为校正到目标尺度的坡度;βmax为实际尺度的最大坡度;dX、dY分别为实际尺度下沿x、y轴的栅格尺寸;ΔX、ΔY分别为目标尺度下沿x、y轴的栅格尺寸;D为分形维数。
将式(2)(3)代入式(1)中,得到地形指数的校正公式为
(4)
式中λsi为校正到目标尺度的流域内某一点地形指数。
1.2 蓄水容量的尺度校正
单点地形指数与蓄水容量之间的关联关系已被广泛认知,通过将上述校正后的地形指数代入蓄水容量与地形指数的定量函数关系式[15,27],即可得到流域各点的蓄水容量:
(5)
式中:Wi为流域内某一点的蓄水容量,mm;Wmax为流域内最大蓄水容量,mm;λmin为流域内最小地形指数;θ、γ分别为网格的尺度参数和形状参数。
基于式(5),采用地形因子推求栅格蓄水容量时,以流域内最大单点蓄水容量Wmax为参数,通过提取流域内各栅格地形指数来推求栅格蓄水容量。
2 实例验证
2.1 研究区概况与资料
以紫罗山水文站上游控制流域(图1,以下简称紫罗山流域)实际资料来验证前文提出的蓄水容量的尺度校正方法(以下简称本文方法)。紫罗山水文站(112°31′E,34°10′N)地处淮河流域沙颍河水系北汝河上游,河南省洛阳市汝阳县小店乡紫罗山坡下,控制面积约为1 800 km2,其中山丘面积约占75%,干流长度约为100 km,平均海拔约为820 m,地形呈西南向东北倾斜的形态。流域属暖温带半干旱大陆性气候,四季分明,1980—1996年多年平均降水量约为900 mm,降水年内分布极不均匀,多集中于6—8月,占全年的60%~70%。

图1 紫罗山流域
研究采用的DEM数据为公开的ASTGTM数据,原始精度为30 m,通过重采样获得分辨率为 50 m、100 m、500 m以及1 000 m的DEM数据作为研究数据。

(a) 目标50 m

(a) 1 000 m分辨率降尺度至50 m
2.2 地形指数降尺度
选取DEM数据的1 000 m分辨率作为实际尺度,分别以50 m、100 m、500 m分辨率作为目标尺度,采用式(4)对实际尺度提取的地形指数进行尺度校正。图2为目标尺度和实际尺度向目标尺度校正的地形指数空间分布,其中,图2(a)(b)(c)(d)为采用4种分辨率直接计算得到的地形指数分布图,图2(e)(f)(g)为以1 000 m为实际分辨率,校正后的50 m、100 m、500 m分辨率地形指数分布图。总体来看,各尺度校正后的地形指数空间分布与目标尺度的直接计算值都较接近。校正50 m分辨率(图2(e))与目标尺度实际50 m分辨率(图2(a))地形指数空间分布最接近。图中绿色为地形指数值较小的区域,黄色部分逐渐增大。整体观察校正前后地形指数的空间分布,实际尺度中浅绿色部分的区域经过校正后颜色有所加深,呈现深绿色,河道中的黄色部分逐渐向浅绿色转变,这表明校正后的地形指数值整体上有变小的趋势,向目标尺度的实际值靠拢。
图3为尺度校正前后地形指数面积分布曲线,可以看出,随着DEM数据分辨率的降低,地形指数面积分布曲线逐渐上移远离横轴,且尺度差异越大,曲线向上偏移越明显。这表明较小的地形指数占比越小,流域各点地形指数差异性越小。校正后地形指数面积分布曲线同目标尺度面积分布曲线呈现出极高的相似性,整体基本重合,曲线上移现象得到纠正,地形指数整体向较小值集中。尤其是地形指数的最小值,如 1 000 m 分辨率降尺度至50 m分辨率结果(图3(a)),最小值基本上减小到1 000 m分辨率的一半,与50 m分辨率结果基本重合。
表1为尺度校正前后地形指数的空间统计特性,可以看出,校正之前随着DEM分辨率的降低,地形指数均值逐渐增加,尺度差异越大,地形指数被高估的偏差越明显。校正后的地形指数与目标地形指数之间误差较小,其中校正500 m分辨率的地形指数均值最接近目标500 m分辨率的地形指数均值,最小均值误差只有1.44%;与实际尺度1 000 m分辨率相比,校正后的地形指数均值有所减小,其中校正 500 m 分辨率的地形指数均值最接近实际 1 000 m 分辨率的地形指数均值,均值误差为 -8.64%。这表明上述地形指数尺度校正方法可以有效地降低地形指数计算的偏差。

表1 尺度校正前后地形指数空间统计特性

(a) 目标50 m
2.3 蓄水容量降尺度
选取DEM数据的1 000 m分辨率作为实际尺度,分别以50 m、100 m、500 m分辨率作为目标尺度,采用式(5)对蓄水容量进行尺度校正。图4为目标尺度和实际尺度向目标尺度校正的蓄水容量空间分布,其中图4(a)(b)(c)(d)为采用4种分辨率直接计算得到的蓄水容量分布,图4(e)(f)(g)为以 1 000 m为实际分辨率,校正后的50 m、100 m、500 m 分辨率蓄水容量分布。总体来看,流域河道处的蓄水容量较小(图中对应着绿色区域),而远离河道和流域分水岭部分蓄水容量较大(图中对应着淡蓝色至深蓝色的区域),与实际情况相符。相比实际 1 000 m 分辨率尺度(图4(d)),尺度校正后的分布图中淡蓝色、深蓝色对应的区域颜色有所淡化,在校正50 m分辨率(图4(e))下变化尤为明显,说明校正后蓄水容量整体上有减小的趋势。而与目标尺度相比,尺度校正后蓄水容量分布图中淡蓝色、深蓝色对应的区域较大,但河道处对应的绿色区域也相对较大,因而蓄水容量总体上非常接近。
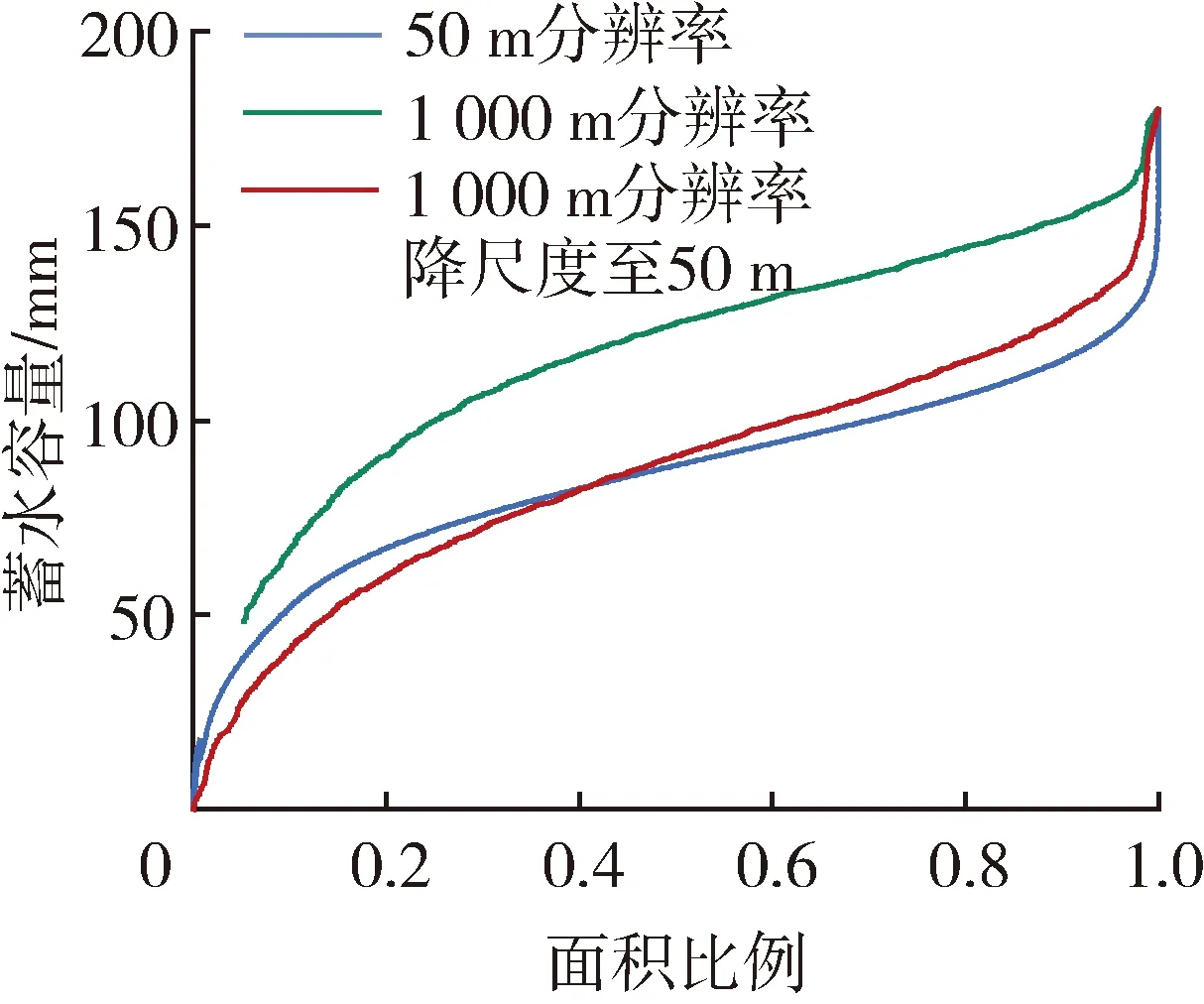
图5为尺度校正前后蓄水容量面积分布曲线,与1 000 m分辨率实际尺度相比,校正后的蓄水容量面积分布曲线逐渐下移,趋近目标尺度,流域平均蓄水容量逐渐减小,由于1 000 m与500 m分辨率尺度在实际提取地形指数时差异较小,因而对应的蓄水容量差异也非常小。
表2为尺度校正前后的蓄水容量空间统计特性,可以看出,校正前流域平均蓄水容量随着DEM数据分辨率的降低不断增大,尺度差异越大,蓄水容量高估的偏差越大。校正后的蓄水容量与各自目标尺度蓄水容量均值误差较小,其中校正500 m分辨率的蓄水容量均值最接近目标500 m分辨率的蓄水容量均值,均值误差只有-1.47%。校正之后,与 1 000 m 分辨率实际尺度相比,校正后的流域平均蓄水容量均有所下降,其中校正500 m分辨率的蓄水容量均值最接近实际1 000 m分辨率的蓄水容量均值,均值误差为-4.00%。可见,考虑地形因素的蓄水容量降尺度方法能够有效地纠正大尺度下蓄水容量高估的偏差,使得蓄水容量的空间分布更接近于实际分布。
(a) 1 000 m分辨率降尺度至50 m

表2 尺度校正前后蓄水容量空间统计特性
3 结 语
不同尺度产流模型的计算偏差与蓄水容量的尺度敏感性有关,这也是导致不同尺度水文响应差异的原因之一。本文在前人研究的基础上,针对蓄水容量提出了相应的尺度校正方法,以地形指数作为辅助因子,通过引入分辨率因子和分形理论分别对决定地形指数的上游集水面积和坡度两个变量进行尺度校正。以紫罗山流域作为实例进行验证,结果表明,上述尺度校正方法不仅能够有效地降低地形指数计算的偏差,使得在低分辨DEM数据条件下可以获得较高分辨率的地形指数分布;而且对蓄水容量的校正效果明显,能够有效地纠正大尺度下蓄水容量高估的偏差,使得蓄水容量的空间分布更接近于实际分布。使用该尺度校正方法不仅可以运用低分辨率的数据获得接近高分辨率数据的计算结果,而且计算量大幅度减小,计算效率得到显著提高,从而可以将分布式水文模型用于实时问题。

