考虑颗粒粒径和液桥体积的毛细力计算方法
张 昭,程靖轩,刘奉银,齐吉琳,许增光
(1.西安理工大学 岩土工程研究所,陕西 西安 710048;2.北京建筑大学 土木与交通工程学院,北京 100044;3.西安理工大学 省部共建西北旱区生态水利国家重点实验室,陕西 西安 710048)
1 研究背景
土坝常因坝前水位骤降而造成坝体滑坡,这种现象与非饱和渗流对土坡变形及其稳定性的影响密切相关[1-2]。土坝在水位骤降时渗流前锋边缘的后退主要受土颗粒间的毛细黏聚作用影响[3],因此,在采用本构模型进行土坝变形分析及其稳定性评价时,如何考虑这种毛细黏聚作用的细观机理值得深入研究。当坝前水位骤降时,在构成土坝的湿颗粒材料中,水分的迁移使其水力与力学行为发生变化,两个表面湿润的颗粒相互靠近时水分会在其接触点及附近区域形成液桥,使颗粒发生连接[4],这种现象取决于毛细黏聚作用[5-6],能够从细观角度反映水分含量对湿颗粒材料变形和强度的贡献[7-8]。若要定量描述湿颗粒材料的毛细黏聚作用机制,则可将其简化为一对不等径球体湿颗粒,采用液桥描述湿颗粒间吸附的水分形态,通过分析液桥的几何形状与受力形态来构建液桥断裂距离及其毛细力关于其体积和颗粒间距的关系式[9-12]。由图1可知,在湿颗粒材料因水位骤降从完全饱和状态开始减湿的过程中,水分会经历毛细状态(颗粒被水分完全浸没)、索带状态(形如索带状液桥的水分至少同时与3 个颗粒相连)和钟摆状态(形如钟摆状液桥的水分仅与两个颗粒相连)[5,13]。本文仅以钟摆状液桥为研究对象,并认为其表面关于水平轴对称,处于拟静力平衡状态,不考虑黏滞作用和重力作用[14]对其力学特征的影响。
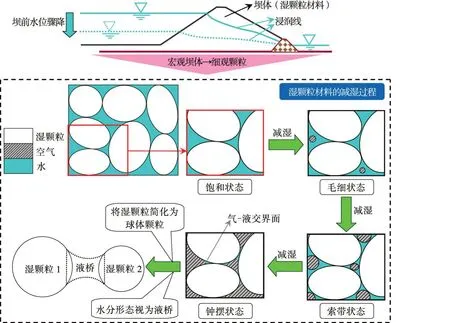
图1 坝前水位骤降时湿颗粒与水的相互作用原理
液桥的力学特征取决于其表面几何形状[9,11-12,15],已有学者通过湿颗粒间液桥拉伸试验研究[10,16-20]表明Young-Laplace 方程能准确描述液桥表面几何形状,并可认为其表面平均曲率为常数。求解Young-Laplace 方程可得到液桥的几何特征、断裂距离和毛细力[9,11-12,15]。
学者们主要采用以下4种方法研究湿颗粒间液桥的断裂距离及其毛细力:①液桥拉伸试验[10,16-17,19,21]:虽可直接测定液桥断裂距离及其毛细力,却需在试验过程中避免重力和颗粒表面粗糙度的影响;②Young-Laplace 方程的数值解[9-12]:只要对这种非线性方程进行合理地离散化,则求取的数值解在允许误差范围内较为准确;③曲线拟合公式[10-11]:依据液桥拉伸试验与Young-Laplace 方程数值解的数据组构建,虽能在较大的液桥体积与颗粒间距范围内实现快速、准确计算,但需标定拟合参数;④半解析-半数值方法[12,22-28]:对液桥表面形状进行简化假定,故具有明确的物理意义,在液桥体积与颗粒间距的一定范围内预测较为准确。
此外,依据上述4 种方法的研究成果亦可知:颗粒粒径对液桥的几何特征与受力状态影响显著。一方面,当采用大、小颗粒半径之比(下文简称颗粒半径比)描述这种影响时,液桥的毛细力会随颗粒半径比增大呈递增趋势[10,16]。另一方面,在曲线拟合与半解析-半数值方法中,常采用颗粒等效半径将等径湿颗粒间液桥的断裂距离及其毛细力公式推广至不等径湿颗粒的情况[10-11]中,颗粒等效半径Re可用大、小颗粒半径(R1和R2)表示为:

式中:当湿颗粒半径相同时,R1=R2=R(mm),则Re=R。值得注意:Willett 等[10]依据Young-Laplace方程数值解分析了采用颗粒等效半径描述不等径湿颗粒间液桥断裂及其毛细力变化特征的准确性,结果发现:采用颗粒等效半径预测的小体积液桥毛细力误差小于2%,而对大体积液桥毛细力的预测误差高达20%;此外,Willett 等[10]发现采用颗粒等效半径预测的液桥断裂距离相对偏大,进而对相应的Young-Laplace 方程数值解进行曲线拟合构建了液桥断裂距离关于其体积、固-液接触角和颗粒半径比的拟合公式。类似地,Lian 等[11]也对Young-Laplace 方程数值解进行曲线拟合,虽得到了适用于小体积液桥断裂距离及其毛细力的计算公式,却因未考虑颗粒半径比的影响而不适用于不等径湿颗粒间的大体积液桥。
不仅如此,半解析-半数值方法大都假定液桥表面在二维平面内形如圆弧(即圆弧假定)[22-24,26-28]。该假定使用简便,但毛细力在液桥最窄“颈部”和颗粒-液桥接触点处不同的现象与Young-Laplace 方程中液桥表面的平均曲率及其毛细力均为常数的性质不符[9,12]。为此,Kruyt 等[12]假定等径湿颗粒间液桥表面在二维平面内形如椭圆弧(即椭圆弧假定),不仅考虑了Young-Laplace 方程中液桥表面平均曲率为常数的性质,而且无需引入拟合参数。然而,Kruyt 等[12]仅以等径湿颗粒间的小体积液桥为研究对象,未考虑不等径颗粒间的大、小体积液桥情况。
为此,以湿颗粒内形如液桥的水分形态为研究对象,从颗粒粒径和液桥体积这两个影响因素出发,将解析表达式推导与Young-Laplace 方程数值解的数据拟合分析相结合,力图提出不等径湿颗粒间的大、小体积液桥断裂距离及其毛细力的计算方法。首先,将文献[12]中针对等径湿颗粒间小体积液桥基于椭圆弧假定构建的解析公式推广至不等径湿颗粒的范围;其次,分析颗粒等效半径在不同颗粒半径比、液桥体积、颗粒间距和固-液接触角条件下的适用性;最后,构建考虑颗粒半径比的断裂距离拟合公式,并改进已有的毛细力拟合公式,使之也适用于大体积液桥,同时,将已有的与改进的拟合公式预测结果进行对比分析。本文提出的毛细力计算方法可为水位骤降时土坝的变形分析及其稳定性评价提供一种综合考虑细观毛细黏聚作用机理与饱和度变化过程的坝体材料本构计算途径。
2 湿颗粒间液桥的几何形状及其Young-Laplace 方程的数值解
本节先描述不等径湿颗粒间钟摆状液桥的几何形状及控制其表面形状的Young-Laplace 方程,进而提出针对不等径湿颗粒的Young-Laplace 方程数值求解方法,构建高精度数值解的数据组,不仅可验证椭圆弧假定,而且可用于分析不同颗粒半径比的湿颗粒在不同颗粒间距下形成大、小体积液桥的断裂及其毛细力变化特征。
2.1 液桥的几何形状从理论上分析不等径湿颗粒间钟摆状液桥应满足的几何条件。先将湿颗粒简化为图2所示一对半径分别为R1和R2(R1≥R2,下标1 和2 分别表示大、小颗粒)的球体颗粒,不考虑颗粒的重力和浮力作用,球体颗粒被液桥不完全浸润,故需考虑固-液接触角θ。依据文献[29],θ值主要受湿颗粒的矿物成分影响,而在进行土坝的渗流与变形计算时常选取同种湿颗粒材料构筑坝体[1,3],因此本文认为这对不等径湿颗粒的矿物成分相同,则液桥对大、小颗粒的θ值相同。关于液桥的表面形状,当其体积较小时(VL∗B≤1×10-3,VL∗B为无量纲液桥体积,详见2.3 节),可将其假定为椭圆弧;当其体积较大时(VL∗B>1×10-3),可采用Young-Laplace 方程数值解描述,详见第3-4 节。这对不等径湿颗粒与液桥的位置关系亦如图2所示:大、小颗粒的中心分别为O1和O2,β1和β2分别为液桥对大、小颗粒的充填角;P1(xc1,yc1)和P2(xc2,yc2)分别为大、小颗粒与液桥的接触点;液桥关于x轴对称,其表面形状可用函数y(x)描述,实质表示液桥在对称轴上任意位置x处的局部半径y,以其y≥0 的上半部分为研究对象,令液桥最窄“颈部”(呈圆形截面)位于x=0 处,此处y的最小值称为液桥的最窄“颈部”半径y0;大、小颗粒至x=0 处的间距分别为d1和d2。由图2亦可知,液桥表面形状函数y(x)在其最窄“颈部”处满足如下条件:
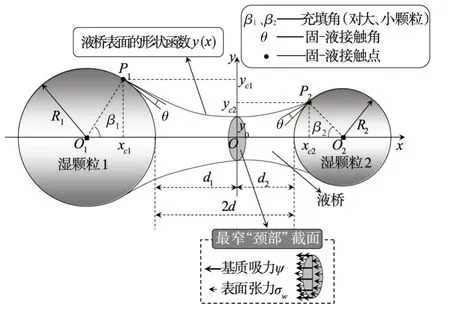
图2 不等径湿颗粒钟摆状液桥的几何参数及其受力状态

式中:y′(x)=dy/dx。接触点P1和P2的坐标可分别表示为:
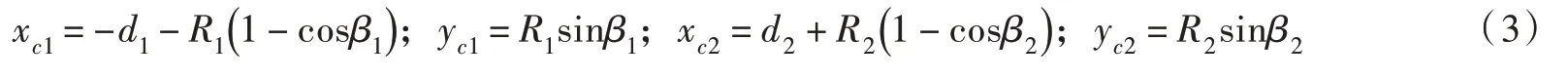
当两个颗粒-液桥接触半径(yc1和yc2)较小时(yc1/R1≪1 且yc2/R2≪1),式(3)可近似为:

此外,依据文献[28],y(x)在两个接触点处的斜率(y′(xc1)和y′(xc2))与θ有关(图2):

式中:ξ=tanθ。需注意:本文仅讨论凹形钟摆状液桥,因此β1和β2与θ需满足β1+θ≤90°和β2+θ≤90°。
2.2 Young-Laplace 方程与液桥的受力状态依据文献[10,16-20],液桥表面形状可用Young-La⁃place 方程描述,依据该方程可认为液桥表面平均曲率为常数。本文以轴对称液桥为研究对象,则表征其表面形状的Young-Laplace 方程为:
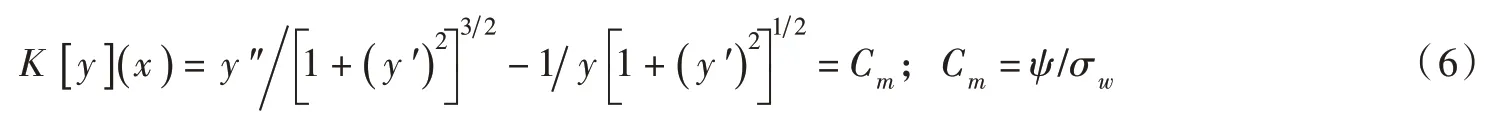
式中:K[y]为平均曲率算子;y′=dy/dx;;Cm为平均曲率,m-1;ψ表示基质吸力,kPa,即横贯于气-液交界面内外的压力差;σw为水分的表面张力(20 ℃时纯水的σw=0.0728 N/m)。该非线性二阶常微分方程的边界条件如式(2)、式(3)和式(5)所示。
对式(6)所示Young-Laplace 方程求积分可得[12]:
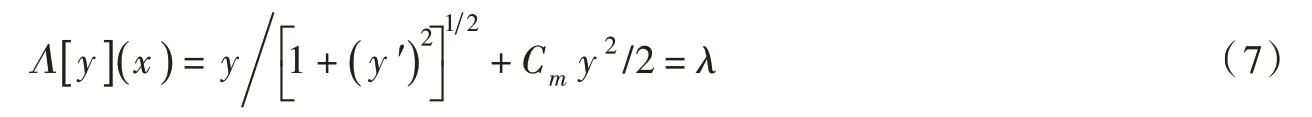
式中:λ为毛细长度系数,mm。Λ[y]为对K[y]的第一次积分结果。式(7)描述了液桥沿其长度方向的受力平衡条件[11-12]。将式(2)和式(5)代入式(7),则Cm和λ可表示为:
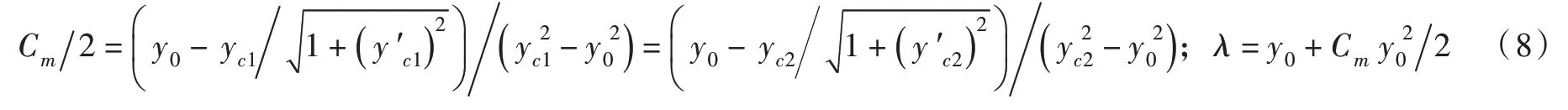
关于液桥的受力状态,选取液桥的最窄“颈部”截面进行分析,亦如图2所示,相应的毛细力F(mN)由作用在该截面周的表面张力σw和截面内的基质吸力ψ共同产生:

将式(6)所示ψ与σw的关系式和式(8)所示λ的公式代入式(9),即可进一步将F表示为:
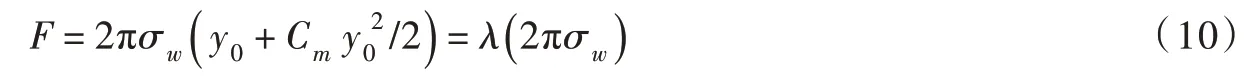
由式(8)可知,y0与yc1和yc2之间存在联系。将式(5)代入式(8)可得这三者之间的关系式:
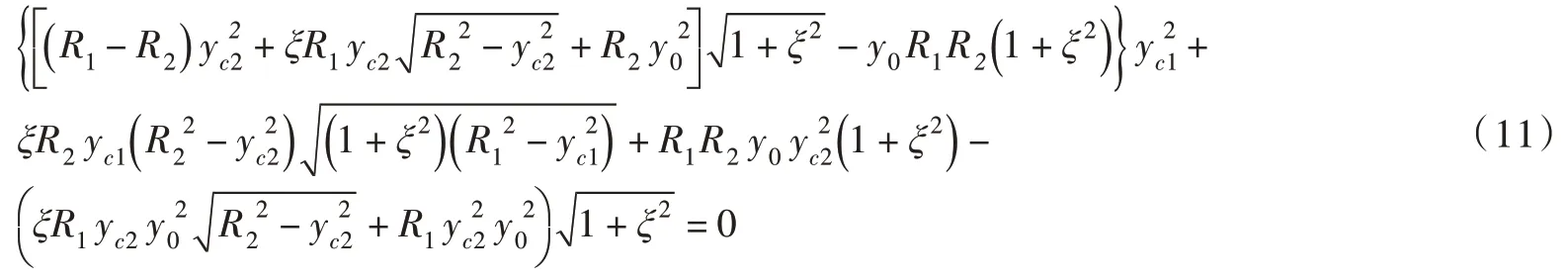

式中:系数δ4、δ2和δ0可用y0、yc2、R1、R2和ξ表示为:
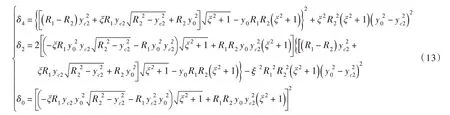
当两个颗粒半径相同时(R1=R2),式(12)有唯一解yc1=yc2,此时液桥也关于y轴对称。表征式(12)所示方程存在实解的判别公式为Δ=δ22-4δ4δ0。该方程存在两个实解(Δ>0)、一个实解(Δ=0)或无实解(Δ<0)均需满足条件yc2≤yc1≤R1。当存在两个实解时,仅液桥表面积较小(其表面能较小)的解有物理意义[12]。式(12)关于大颗粒-液桥接触半径yc1存在实解时液桥最窄“颈部”半径y0和小颗粒-液桥接触半径yc2的取值区域如图3所示,实质上给出了R1/R2= 1、2 和128 且θ=0°和20°时的上、下限。
当yc2和y0较小时,方程判别式Δ为零,且Δ可近似表示为:
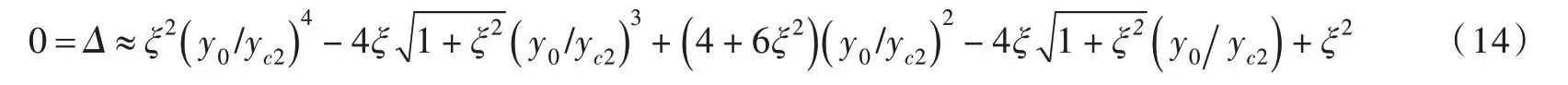
式(14)可在yc2和y0处进行泰勒展开,而与颗粒半径比无关。当ξ给定时,求解式(14)可得的最小值,即图3中下边界在yc2=0 处的斜率。由图3可知,当较小时且大于1 时,下边界基本不受影响。需注意:当较大时,与θ会显著影响式(12)关于yc1存在实解的区域,故不同与θ条件下式(12)关于yc1存在实解区域的显式公式有待进一步研究。
2.3 Young-Laplace 方程的数值解式(6)所示Young-Laplace 方程的数值解可依据如下方法求取。当给定两个颗粒-液桥接触半径(yc1和yc2)与液桥的最窄“颈部”半径y0时,平均曲率Cm和毛细力系数λ可由式(8)确定。由式(7)可知,y′=dy/dx可表示为y的函数,则液桥表面形状函数y(x)可通过dx/dy=1/(dy/dx)求得其反函数x(y),进而将Kruyt 等[12]计算等径湿颗粒间液桥表面形状x(y)的积分公式推广至不等径湿颗粒。该函数在x<0 和x≥0 时的斜率(dx/dy)分别为负值和正值(图2),故可分为x1(y)(x<0)和x2(y)(x≥0)两部分,依据式(7)得到x1(y)和x2(y)的积分公式:
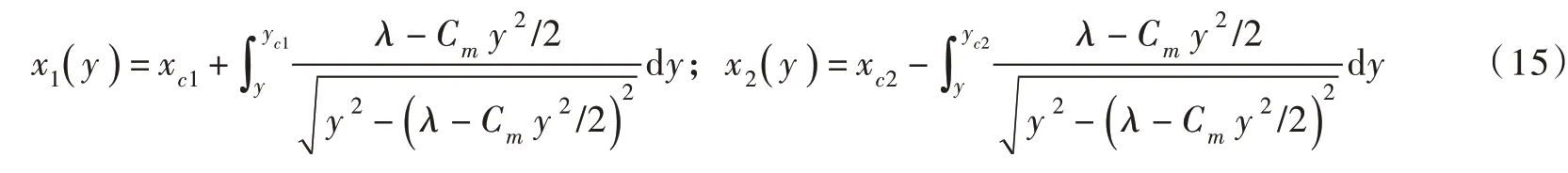
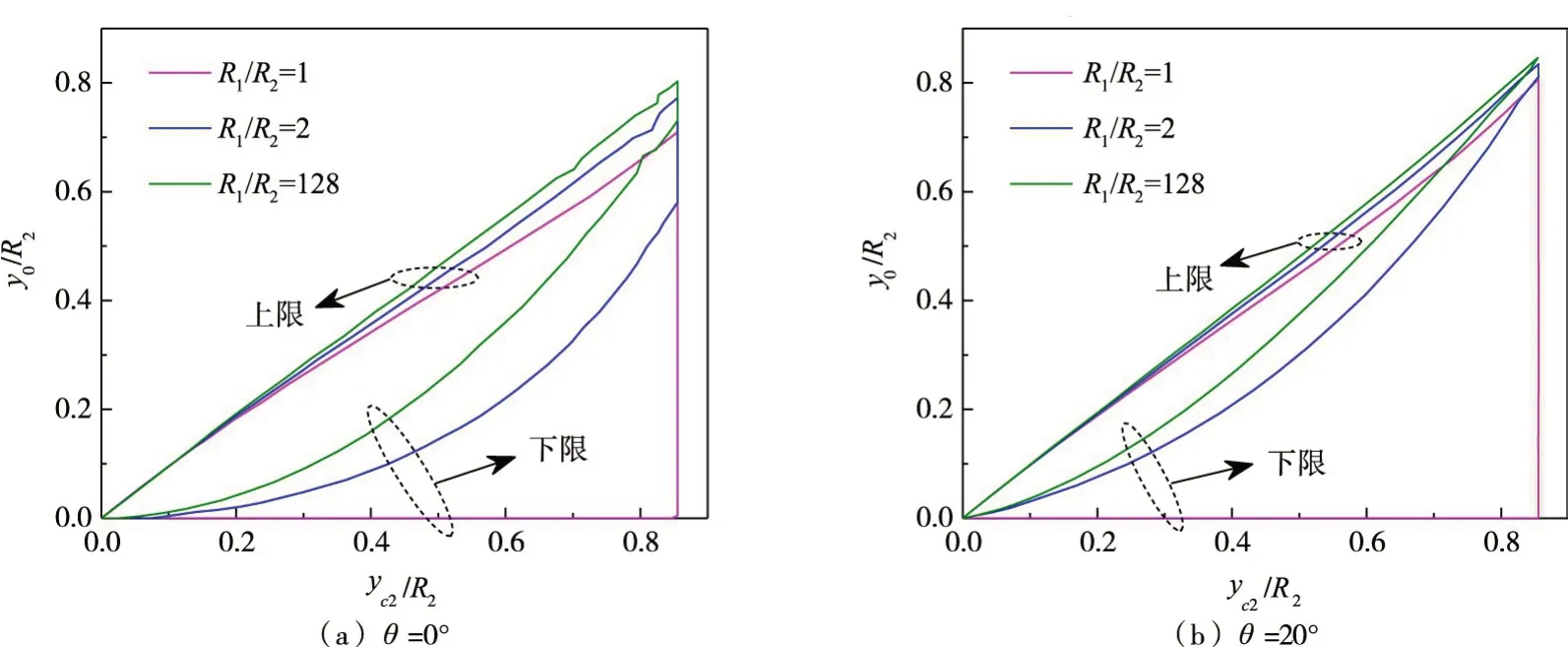
图3 式(12)关于yc1 存在实解时y0 和yc2 的取值区域
由于Kruyt 等[12]采用的Gauss-Kronrod 自适应数值积分算法可解决式(15)在y0处积分出现的弱奇点问题,故采用该算法(令计算中的相对误差限为10-6)计算式(15)中的积分,即可得到y(x)。从大、小颗粒与液桥的接触面至液桥最窄“颈部”处(x=0)分别对应的液桥体积(VLB1和VLB2)可通过对y(x)进行数值积分得到:
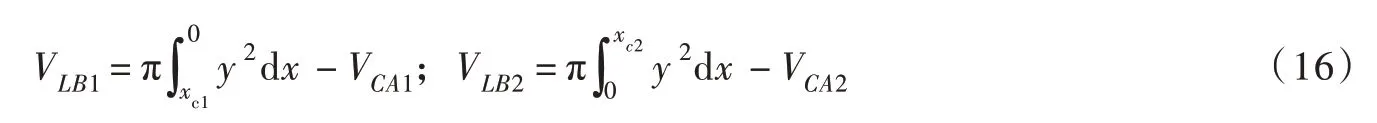
式中:VCA1和VCA2分别为大、小颗粒被液桥浸润的球冠体积,可表示为:
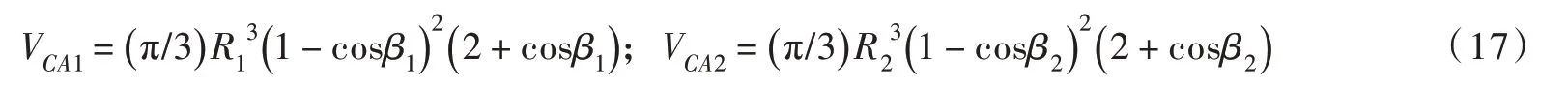
液桥体积VLB(μL)及颗粒间距2d(mm)可由大、小颗粒对应的液桥体积及颗粒间距(d1和d2)求和而得:

由此可依据颗粒等效半径Re定义无量纲液桥体积VL∗B(VL∗B =VLB/Re3)和无量纲颗粒间距2d∗(2d∗=2d/Re)。
因此,可依据本节上述计算方法对Young-Laplace 方程求得下列条件下的不同数值解:①在充填角β低于60°的范围内取500 个不同数值;②液桥最窄“颈部”半径及其与小颗粒接触半径之比y02在0~1 范围内取500 个不同数值;③颗粒半径比R1R2=1、4/3、2、4、8、16 和128;④固-液接触角θ=0°、20°、40°。
将上述条件下的不同数值解构成数据组,要求在y02=0~1 的范围内仅考虑如图2所示的凹形钟摆状液桥,而且忽略颗粒间距2d为负值时的无物理意义数值解(2d可通过y0、yc1和yc2算得)。由于该数据组存储了每个β和y0yc2对应的2d、VLB、F和Cm,因此,一方面可将Cm代入式(6)算得相应的ψ,另一方面可依据Kruyt 等[12]提出的数值线性内插方法算得VLB和2d任意取值组合对应的F,从而为验证、评价本文以下提出的液桥断裂距离及其毛细力的解析与拟合公式提供数据支撑。
3 基于椭圆弧假定计算不等径湿颗粒间小体积液桥的断裂距离及其毛细力
所谓椭圆弧假定,即在二维平面内采用椭圆弧描述湿颗粒间液桥的表面形状,该假定已用于研究等径湿颗粒间小体积液桥的断裂及毛细力变化特征[12]。本节将椭圆弧假定推广至不等径湿颗粒间形成的液桥:先阐述如何采用椭圆方程描述不等径湿颗粒间液桥的表面形状,以讨论椭圆弧假定的适用性;继而取液桥内毛细力为常数,构建相应的几何关系式,从而确定基于椭圆弧描述液桥表面形状所需的几何参数;再推导颗粒-液桥接触半径、液桥断裂距离及其毛细力关于液桥体积和颗粒间距的解析公式,通过对比分析解析公式对不同液桥断裂距离及其毛细力的Young-Laplace 方程数值解的预测效果,旨在验证采用颗粒等效半径将等径湿颗粒间小体积液桥的断裂距离及其毛细力解析公式推广至不等径湿颗粒范围的适用性。
3.1 基于椭圆方程描述不等径湿颗粒间液桥的表面形状椭圆弧假定可用于描述等径湿颗粒间液桥
的表面形状[12]。然而,对不等径湿颗粒间的液桥,当给定其体积与颗粒间距时,采用椭圆弧描述其表面形状时边界条件较多(将在3.2 节讨论),故不能仅用一段椭圆弧描述。为此,这里采用两段与大、小颗粒相对应的椭圆弧来描述液桥的表面形状函数y(x):

式中:i=1、2 分别表示大、小颗粒;ai和bi分别为长、短半轴距;(0,ni)为椭圆的中心。依据式(2)和式(5)所示边界条件,可求得式(19)中的几何参数ni、ai和bi(i=1,2):
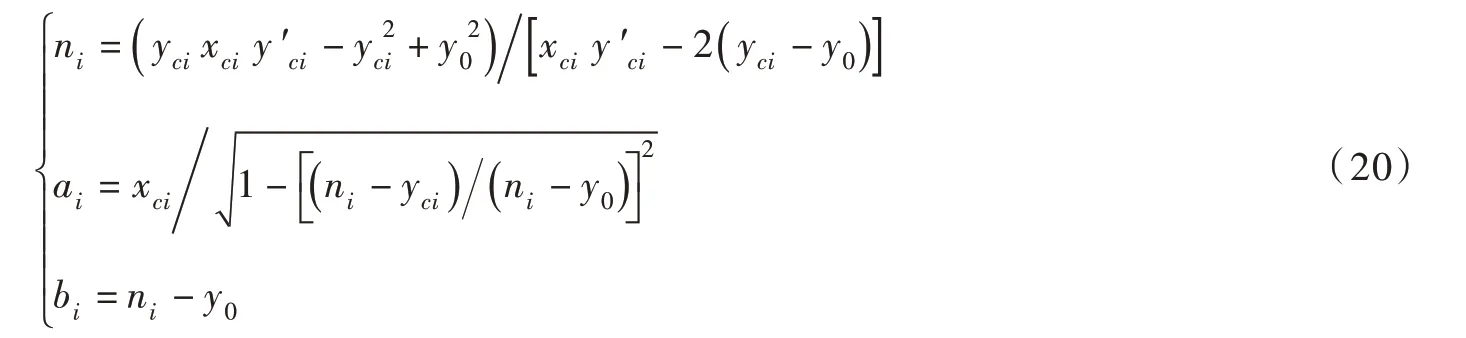
为评价采用椭圆弧描述不等径湿颗粒间液桥表面形状的精度,可对比分析基于椭圆弧假定的不同颗粒半径比R12的湿颗粒间液桥对Young-Laplace 方程数值解的预测效果,如图4所示,椭圆弧能较为准确地描述不同R12的湿颗粒间小体积液桥(VL∗B≤1×10-3)在θ≤20°时的表面形状。
由于接触点横坐标xci和最窄“颈部”半径y0均随颗粒-液桥接触半径yci变化,故依据文献[12]的无量纲方法引入以下两个无量纲变量:

式中:χi为无量纲接触点坐标;ηi为液桥最窄“颈部”半径与颗粒-液桥接触半径之比。当液桥表面形状确定时,χi和ηi分别满足χi≥0 和0 ≤ηi≤1。
将式(2)、式(4)、式(5)和式(21)代入式(20),并在小变量yci/Ri处进行泰勒展开,则ni、ai和bi可近似表示为:

当两个颗粒半径相同时(R1=R2),ni、ai和bi的公式同文献[12];当ai =bi时,椭圆弧转化为圆弧,即椭圆弧假定退化为圆弧假定,则χ与η的关系为:

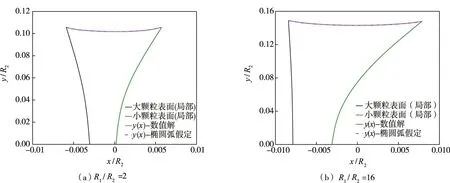
图4 液桥表面形状函数y(x)的数值解及椭圆弧假定的预测结果(θ =20°且VL∗B ≤1×10-3)
3.2 液桥表面形状的补充几何条件和封闭关系式基于椭圆弧假定描述等径湿颗粒间液桥的表面形状时,较圆弧假定不同之处在于需要构建无量纲变量χ与η的封闭关系式来确定椭圆弧的自由参数[12]。当一对湿颗粒R1=R2时,可通过补充平均曲率在液桥最窄“颈部”与颗粒-液桥接触点处取值相同的几何条件来构建封闭关系式。反之,由于其间液桥关于x=0 的最窄“颈部”处不对称,则这种平均曲率相同的补充几何条件不再适用。因此,对不等径湿颗粒间的液桥表面形状构建封闭关系式时,需补充新的几何条件。
如2.2 节所述,对式(6)所示Young-Laplace 方程积分可得到式(7)所示算子Λ[y](x)(相应的毛细力沿轴向不变),故Young-Laplace 方程与式(7)是等效的。当控制液桥最窄“颈部”半径y0和小颗粒-液桥接触半径yc2时,欲通过式(12)确定大颗粒-液桥接触半径yc1(若yc1的解存在),则需满足Λ[y](xc1)=Λ[y](xc2),由此可实现Λ[y](xc1)=Λ[y](0)=Λ[y](xc2),进而依据Λ[y](x)在不同x处相同的原则补充几何条件。为此,针对描述液桥表面形状的两段椭圆弧,依据Λ[y](x)在液桥最窄“颈部”与颗粒-液桥接触点之间中点处相同可补充两个几何条件:

式中:i=2 时的几何条件因在式(12)的推导过程中已考虑而得以满足。 由式(24)可知Λ[y](xc1/2)=Λ[y](xc2/2),则x=xc1、xc1/2 、0、xc2/2 和xc2处的毛细力均沿轴向相等,因此式(24)所示两个补充几何条件因Λ[y](x)为常数而考虑了Young-Laplace 方程的性质。需注意:这两个几何协调条件仅考虑对液桥表面形状函数的一阶导数y′(x),不同于文献[12]中考虑对液桥表面形状函数的二阶导数y″(x)。
将式(22)所示参数ni、ai和bi代入式(19),同时联立式(24)推得无量纲变量χi与ηi之间的封闭关系式:

式中:g(χi,ηi)具体表示为:
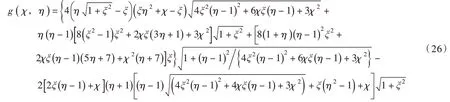
由于封闭关系式的函数对应法则对大、小颗粒均为g,即g(χ1,η1)=0 、g(χ2,η2)=0 。为符号表述简便,故下文统一采用g(χ,η)=0 的形式。
当χ≥0 、 0 ≤η≤1 且(θ≤60°) 时,g(χ=0,η)≤0 且∂g(χ,η)/∂χ≥0。因此,若给定η值,则式(26)所示χ的方程有唯一非负解,这个具有物理意义的唯一解可表示为χ=f(η)的函数形式。在固-液接触角θ分别取0°和20°、颗粒半径比R1/R2分别取4/3 和16、无量纲液桥体积分别取VL∗B≤1×10-6和≤1×10-3条件下,整理χ与η关系的Young-Laplace 方程数值解与式(25)所得χ=f(η)函数及圆弧假定(式(23))的预测曲线,如图5所示:当η=η∗时,封闭关系χ=f(η)存在峰值χ∗,可将(η∗,χ∗)称为界限点;当χ值一定时,η=f-1(χ)存在两段,亦如文献[12,15]所述,当η≥η*时,表面积较小的液桥才具有物理意义。由图5(a)(c)可知:当VL∗B≤1×10-6时,大、小颗粒对应的Young-Laplace方程数值解可压缩为一条数据线,其与式(25)所得χ=f(η)函数的预测曲线较为吻合;大、小颗粒对应的界限点(η*,χ*)完全相同。由图5(b)(d)可知,当VL*B≤1×10-3时,Young-Laplace 方程数值解呈一定范围的数据带(并非一条数据线),大颗粒较小颗粒数据带更窄;式(25)所得χ=f(η)函数的预测曲线较数值解偏小,Kruyt 等[12]对等径湿颗粒间液桥亦得到了类似的计算结果。不仅如此,由图5亦可知,当θ≤20°且VL∗B≤1×10-3时,式(25)所得χ=f(η)函数较式(23)所示圆弧假定的预测曲线对不同值的Young-Laplace 方程数值解更吻合。
当计算小体积液桥(V LB≤1×10-3)的毛细力时,需要在η≥η∗的稳定段内对η=f-1(χ)的封闭关系进行近似简化。这里将η=f-1(χ)的封闭关系式近似为:


图5 θ 、VL*B 和R1/R2 不同时 χ 与η 关系的数值解以及由式(25)和式(23)所得预测曲线
式中:函数L(χ)可表示为χ的二次多项式:

式中:k0、k1和k2为方程系数。
式(27)所示近似关系需满足χ=f(η)函数的4 个性质:①f(1)=0 ;②(由图5可知,与式(23)所示圆弧假定在此处的斜率相同);③f(η*)=χ*;④f′()η =0 。因此,式(27)与性质①、②和③对应的约束条件可表示为:
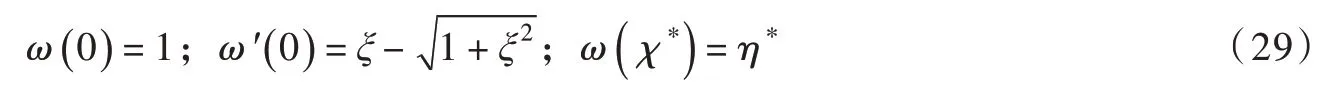
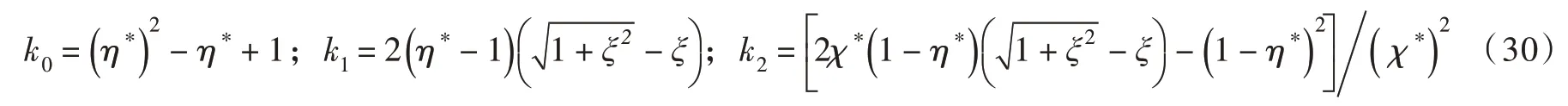
将式(30)代入式(28)所示函数L(χ)中,进而将其代入式(27)即可得到η=f-1(χ)的近似关系:
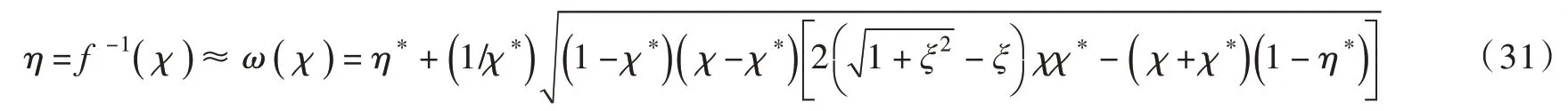
3.3 颗粒-液桥接触半径关于液桥体积和颗粒间距的解析公式若控制液桥体积VLB和颗粒间距2d,为推导适用于小体积液桥的颗粒-液桥接触半径(yc1和yc2)解析公式,可将式(19)所示形如椭圆弧的液桥表面形状函数y(x)代入式(16)—(18)所示液桥体积公式,进而在yc1和yc2较小的条件下对VLB在ξ处得到泰勒展开式:

式中函数j(η)和h(η)可表示为:
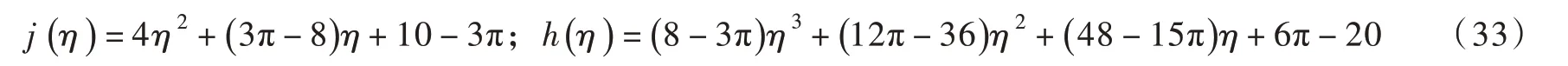
在η≥η∗的η=f-1(χ)稳定段内,j(η)和h(η)可在(χ=0,η=1) 处得到泰勒展开式:

当给定VLB和2d时,式(32)中的yc1和yc2未知,对其求解则需增加yc1与yc2的约束条件,可引入表征颗粒-液桥接触点处毛细力相同的式(11)表示。当yc1≪R1且yc2≪R2时,VLB较小(VL∗B≤1×10-3),又故可在yc2和y0确定时,将式(11)简化为关于yc1的二次方程:
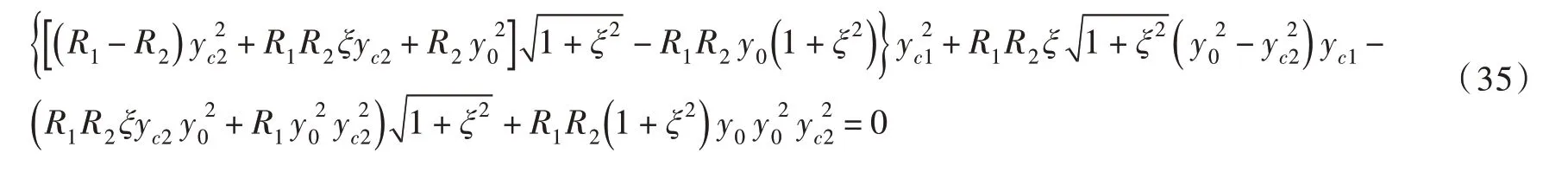
当液桥体积很小时,式(11)和式(35)的解基本相同。将y0=η2yc2(由式(21)可得)代入式(35),并在小变量yc2处得到泰勒展开式:
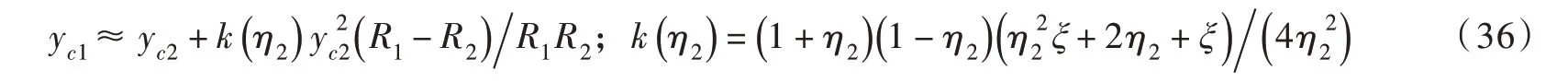
当0≤θ≤45°且0.4≤η2≤1.0 时,函数k(η2)在0 ~2 范围内变化。由于yc2≪R2≤R1,式(36)中的项可忽略不计,故此时大、小颗粒与液桥的接触半径近似相等,即yc1≈yc2,这与图4所示小体积液桥(VL∗B≤1×10-3)与大、小颗粒的接触特征一致。由该近似条件可知,η1≈η2(依据式(21)),进而依据式(25)所示封闭关系可知χ1=f(η1)≈f(η2)=χ2。因此,可将式(32)进一步整理为VLB关于yc2的公式:
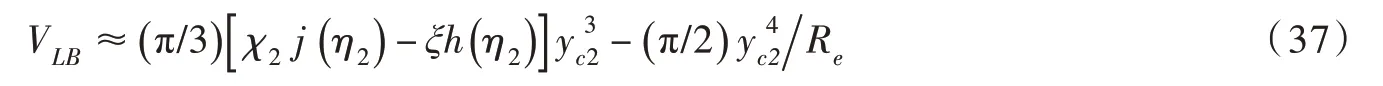
式中:Re为颗粒等效半径,同式(1)。由yc1≈yc2和η1≈η2可知xc1≈-xc2(依据式(21))。将该近似条件代入式(4)和式(18),即可得到小颗粒至x=0 处的间距d2(图2)公式:

将式(34)代入式(37),并联立式(4)、式(21)、式(30)和式(38),把式(37)进一步整理为VLB和2d一定时关于yc2的五次方程:
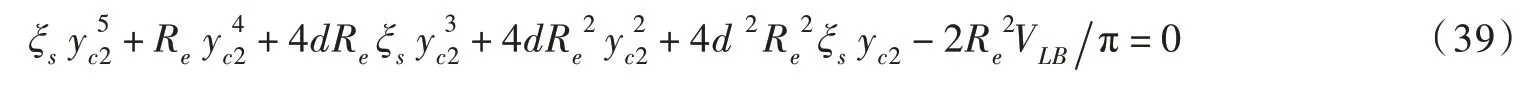
式中:ξs为关于ξ的公式缩略代换变量:
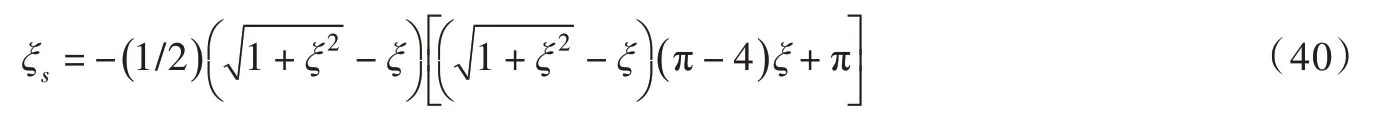
当0≤θ≤60°且yc2≪Re时, -π/2 ≤ξs≤-3/10,则式(39)中yc2的五次方项较其四次方项可忽略,而yc2的三次方项较其平方项可忽略,由此可将式(39)简化为四次方程:
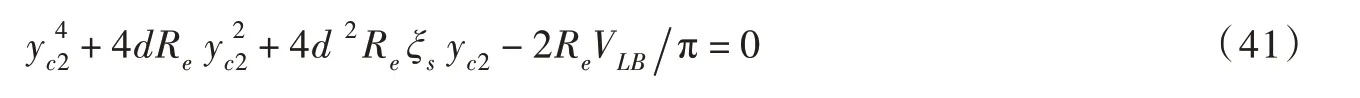
依据文献[12],式(41)关于yc2的解可在颗粒间距较小和较大两个范围内分别求取。采用文献[12]所述联立方法,将式(41)的解表示为:
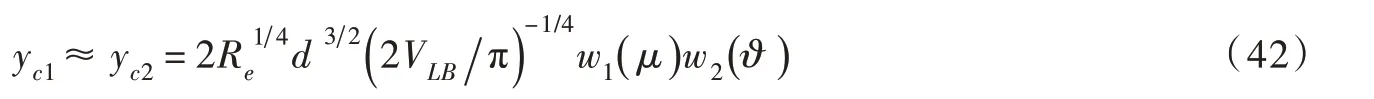
式中:μ(不同于文献[12])、ϑ、w1(μ)和w2(ϑ)分别表示为:

需注意:如式(42)所示,yc1和yc2仅通过Re反映了大、小颗粒半径(R1和R2)的影响。
3.4 小体积液桥断裂距离的解析公式已有试验[10,16]表明:湿颗粒间的液桥会随颗粒间距增大而逐渐拉伸直至断裂,而液桥断裂距离2dr与其体积VLB和固-液接触角θ有关,并与Young-Laplace 方程出现唯一数值解时的数据点对应[9-10,12]。依据文献[12], 2dr随其VLB和θ的变化关系亦可采用椭圆弧假定预测。
由图5中式(25)所示封闭关系χ=f(η)可知,χ在0≤η≤1 范围内存在峰值,该峰值点(或界限点)的坐标用(η*,χ*)表示,相应的j(η)值和h(η)值(函数公式如式(33)所示)分别用j∗和h∗表示。由于不等径湿颗粒间液桥即将断裂时其体积很小,yc2≪Re,则式(37)中yc2的四次方项可忽略,由此可将式(37)所示VLB的公式进一步简化为:

此外,当(η,χ)位于界限点(η∗,χ∗)时,yc较小且d=dr,联立式(4)(21)(38)可得χ∗关于dr和yc2的近似公式:

由此,联立式(44)和式(45)可得到2dr的解析公式:
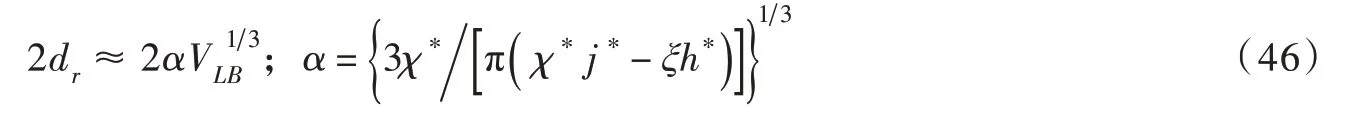
式中:不同θ值对应的χ∗和η∗∗值(由式(25)确定)、j∗和h∗值(由式(33)确定)如表1所示。此外,对比文献[9]和式(46)中系数α在0≤θ≤20°范围内的取值,如图6所示,式(46)计算的α值与文献[9]差异较小,不超过7%。
3.5 小体积液桥毛细力的解析公式针对不等径湿颗粒间形成的小体积液桥,采用椭圆弧假定,推导液桥毛细力关于其体积和颗粒间距的解析公式(无需引入任何标定的拟合参数)。由式(10)可知,计算毛细力F的关键在于求解毛细长度系数λ,λ可通过液桥最窄“颈部”半径y0、颗粒-液桥接触半径(如yc2)及其接触点斜率(如y′c2)计算得到。若控制液桥体积VLB、颗粒间距2d和固-液接触角θ,当VLB较小时,颗粒-液桥接触半径(yc1≈yc2)可由式(42)确定;小颗粒至x=0 处的间距d2(图2)由式(38)确定,再通过式(4)和式(21)确定χ2,进而将χ2、χ∗和η∗值(依据表1查取的)代入式(27)以确定η2;将η2代入式(21)即可确定y0,继而由式(5)确定y′c2;将y0、yc2和y′c2代入式(8),并在yc2处进行泰勒展开,从而得到λ的解析公式:
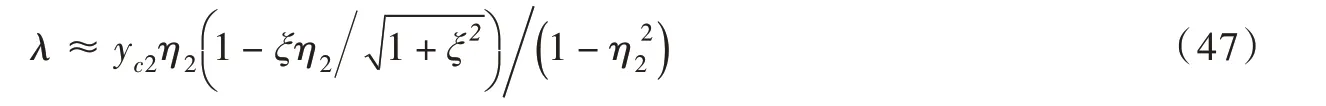
最后,将式(47)代入式(10)确定F;若采用颗粒等效半径Re对F无量纲化,结合式(47)亦可确定无量纲毛细力F*(F=λ/Re)。
整理不同颗粒半径比(R1/R2=2 和128)的湿颗粒间液桥取不同无量纲体积(体积较小,VL∗B=1×10-6和1×10-3)和颗粒间距之比d∗/dr∗(d*和dr∗分别为无量纲的颗粒半间距和液桥断裂半倍距离)时无量纲毛细力F*的Young-Laplace 方程数值解及式(47)的预测值,如图7所示(R1/R2=128 可近似视为球体与片状湿颗粒之间形成的液桥),式(47)对Young-Laplace 方程数值解的预测较为吻合:当d*<0.6dr∗时,VL∗B=1×10-6和1×10-3时的预测误差分别小于5%和6%;当d*≥0.6dr∗时,预测误差虽有所增大,但此时F*已很小。原因可能在于:当颗粒间距较大时,大、小颗粒与液桥的接触半径差异显著,因此依据yc1≈yc2条件所计算的F*值较Young-Laplace 方程数值解势必会产生误差。此外,当d*≥0.6dr∗时,极小体积液桥(VL∗B=1×10-6)对应的Young-Laplace 方程数值解及式(47)的预测值会出现波动(4.2 节的图12(a)亦有此现象)。原因可能在于:液桥表面的自由能对其稳定性影响显著[9],当极小体积液桥被拉伸接近断裂时,会因其表面(尤其在最窄“颈部”处)的自由能过小而无法控制其稳定性,致使波动现象出现;当液桥体积增大时,其表面自由能亦随之增大,从而使这种波动现象逐渐消失(4.2 节的图12(b)—(d)可佐证)。
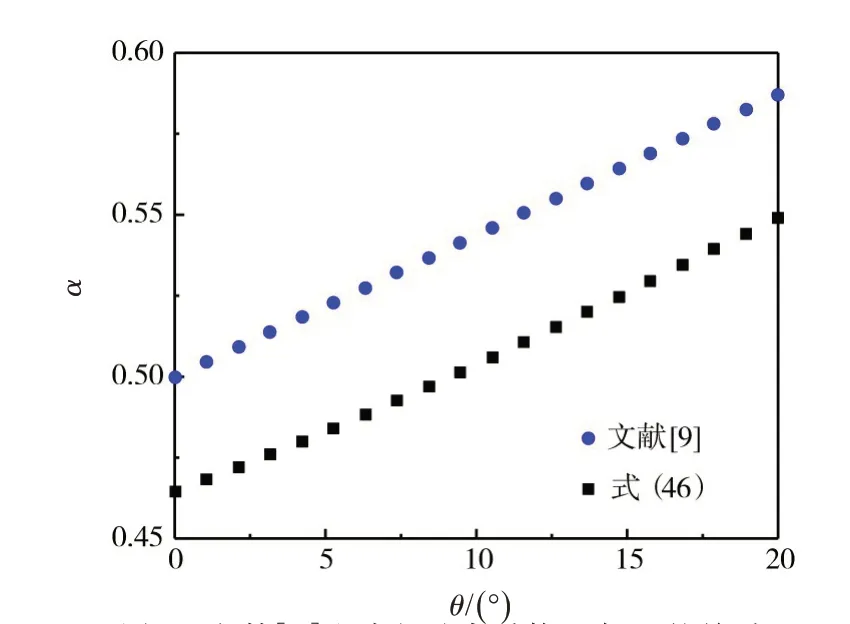
图6 文献[9]和式(46)中系数α 与θ 的关系
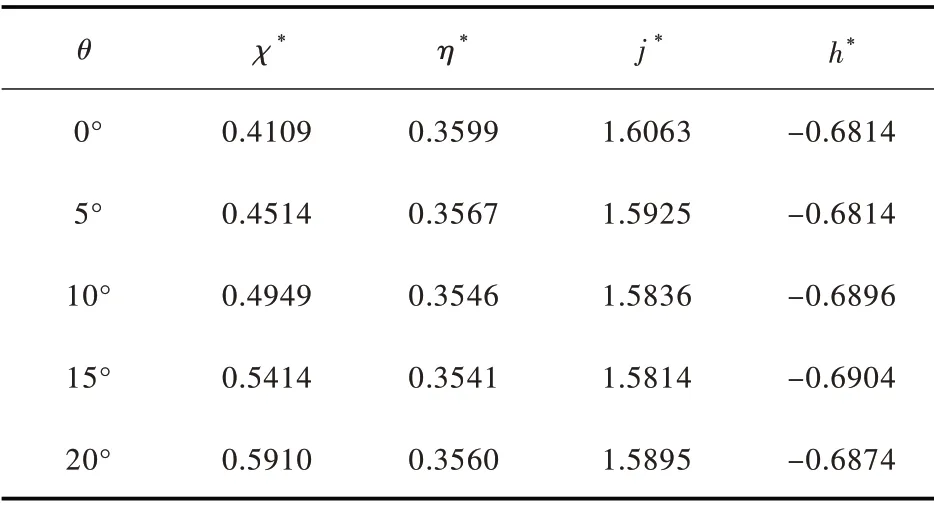
表1 不同θ 值对应的 χ *、η*、 j *和h*值
不仅如此,为从试验角度研究湿颗粒间不同体积液桥(液桥体积亦较小,VL∗B≤1×10-3)的毛细力随颗粒间距的变化特征,Rabinovich 等[16]利用原子力显微镜(AFM)测定了3 对玻璃质球体湿颗粒被液体不完全浸润(θ=10°)时其间形成的液桥(液体选取石蜡油,其表面张力为27.5×10-3N/m)在不同颗粒间距对应的毛细力,其中R1/R2≈1.84、1.71和1.44;VL∗B≈1.3×10-5、8.7×10-5和3.2×10-4;相应的试验编号分别为①、②和③。整理这3 对不等径球体湿颗粒间液桥取不同d*/dr*时F*的实测值及式(47)的预测值如图8所示,式(47)对试验①、②、③中液桥F*的预测值与其实测值较为吻合,预测误差不超过9%,仅当d*≥0.5dr∗时,预测误差虽有所增大,但此时F*已很小,与图7所示预测结果类似。
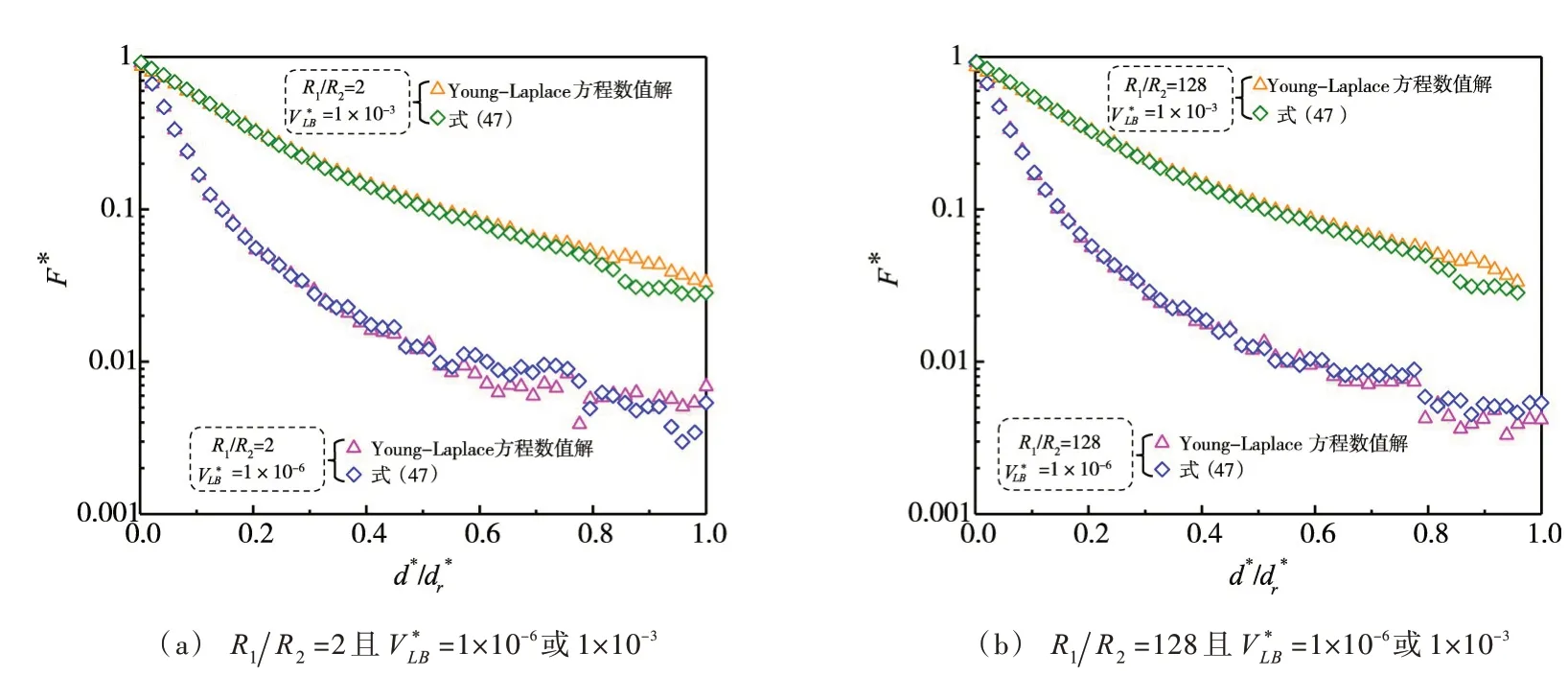
图7 R1/R2、和d */dr* 不同时无量纲毛细力F*的Young-Laplac e 方程数值解及式(47)的预测值(θ =20°)

图8 和不同时F *的实测值及式(47)的预测值(θ =10°)
当给定VLB、2d、θ和颗粒半径(R1和R2)时,则可依据椭圆弧假定按照如下方法计算不等径湿颗粒间小体积液桥(VL∗B≤1×10-3)的F:①检查2d是否小于式(46)所确定的2dr;②依据式(42)由确定的VLB和d计算yc2;③将yc2代入式(38)和式(4),分别计算得d2和xc2;④采用式(21)和式(27)分别得到χ2和η2;⑤联立式(47)和式(10)即可计算出F。
如3.3 节依据椭圆弧假定的分析所述,yc1≈yc2,进而据式(37)所示液桥体积公式可知,yc1和yc2通过式(1)所示Re仅与R1、R2有关。由此可见,当液桥体积较小时,针对等径湿颗粒推得的液桥断裂距离与其毛细力的解析公式可通过Re推广至不等径湿颗粒的情况。这种思路虽已通过对Young-Laplace 方程数值解的分析得以应用[10-11,30],但鲜从解析角度得到论证,为此,本节在椭圆弧假定的小体积液桥适用范围内从解析角度验证了这种思路的准确性,而在大体积液桥断裂距离与其毛细力公式中采用Re的适用性将在下节阐述。
4 基于拟合公式计算大体积液桥的断裂距离及其毛细力
不等径湿颗粒间大体积液桥的断裂距离与其毛细力研究报道较少[10-11],Willett 等[10]选取有限的Young-Laplace 方程数值解数据组构建了液桥断裂距离及其毛细力的拟合公式,Lian 等[11]基于任意颗粒间距时的毛细力与颗粒相互接触(颗粒间距为零)时的初始毛细力之比构建了液桥毛细力拟合公式。然而,由于相互接触的湿颗粒间无法形成较大体积的凹形钟摆状液桥,因此他们[10-11]提出的公式仅适用于小体积液桥,对大体积液桥适用性有限。为此,本节以大体积液桥为研究对象,旨在分析颗粒半径比和固-液接触角对其断裂距离与毛细力的影响。为对比文献[10-11]的研究,本节采用较文献[10]规模更大的Young-Laplace 方程数值解数据组,选取较文献[11]范围更广的液桥体积和颗粒半径比。
当液桥体积和颗粒间距较大时,椭圆弧假定不适于描述其表面形状。为此,基于2.3 节所述Young-Laplace 方程数值解的数据组,采用颗粒半径比而非颗粒等效半径来描述颗粒半径的影响,一方面构建液桥断裂距离的拟合公式,另一方面将Lian 等[11]提出的毛细力公式进行改进,使之适用于大体积液桥。
4.1 液桥断裂距离的拟合公式:从小体积液桥到大体积液桥Willett 等[10]从试验与数值解角度分析了颗粒半径比对液桥断裂距离的影响,依据试验结果阐述了颗粒半径比对大体积液桥断裂距离的影响,进而对有限的Young-Laplace 方程数值解数据组进行曲线拟合,得到了无量纲液桥断裂距离2dr∗的拟合公式:
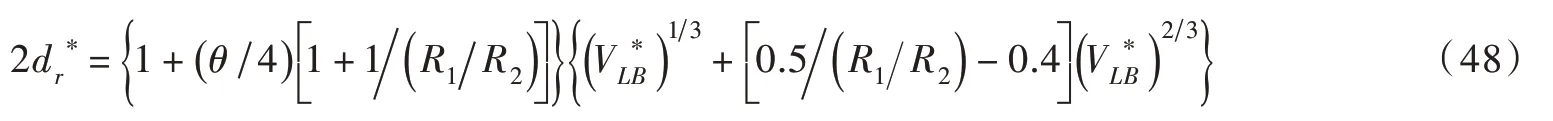
式中:固-液接触角θ用弧度表示;VL∗B为无量纲液桥体积,其与2dr∗的无量纲定义方式如2.3 节所述。对比分析不同颗粒半径比(1≤R1/R2≤128)的湿颗粒间不同体积(0≤≤0.22)液桥在θ=20°、40°时2dr∗的Young-Laplace 方程数值解及式(48)的预测值,如图9(a)(c)所示,式(48)对θ=20°、40°时数值解的预测误差较大(分别为4.5%和10%)。因此,有必要在式(48)基础上通过引入和θ的高阶项以构建适用液桥体积更广范围的无量纲液桥断裂距离拟合公式。通过对2dr∗的Young-Laplace 方程数值解进行曲线拟合可得到2dr∗关于VL∗B、θ和R1/R2的拟合公式:

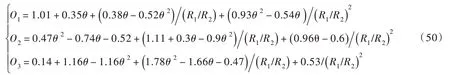
对比分析式(49)对不同颗粒半径比(1≤R1/R2≤128)的湿颗粒间不同体积(0≤VL*B≤0.22)液桥在θ=20°、40°时2dr∗的Young-Laplace 方程数值解的预测结果,如图9(b)(d)所示,式(49)对θ=20°、40°时数值解的预测误差较式(48)显著减小,分别为1%和2%。
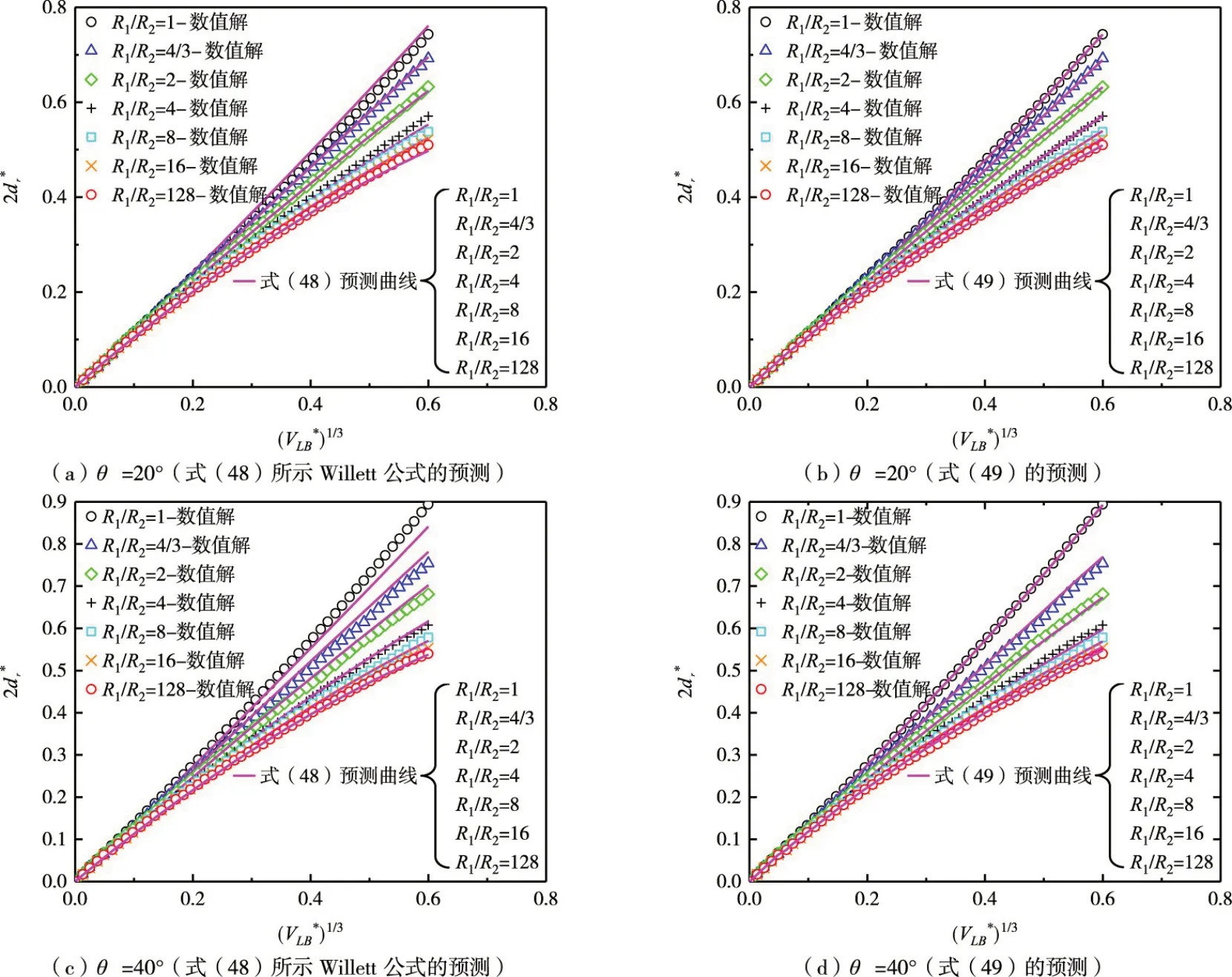
图9 采用式(48)与式(49)对不同R1/R2 和θ 时2dr∗ 的Young-Laplace 方程数值解的预测结果比较
4.2 液桥毛细力的拟合公式评价:从小体积液桥到大体积液桥Willett 等[10]和Lian 等[11]已提出大体积液桥的毛细力拟合公式,这里采用本文构建的Young-Laplace 方程数值解数据组评价其预测精度。
Willett 等[10]通过对Young-Laplace 方程数值解进行曲线拟合,构建了无量纲液桥毛细力F*的拟合公式(F*=λ/Re):
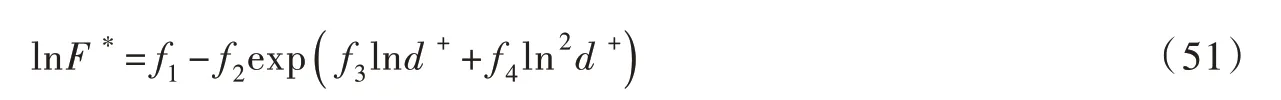
Lian 等[11]先分析了湿颗粒相互接触(颗粒间距为零)时的初始毛细力,进而依据任意颗粒间距与零间距时的毛细力比值构建了F*的拟合公式:
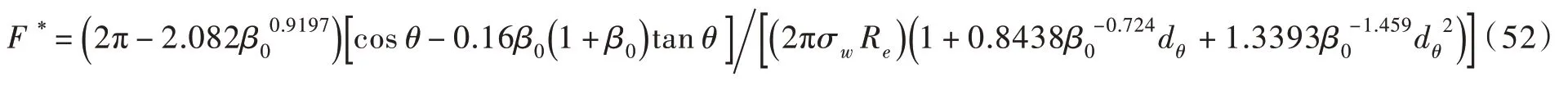
式中dθ可表示为:
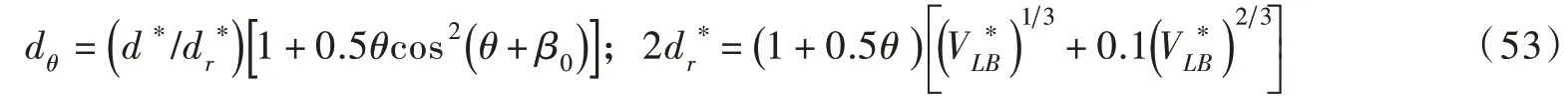
式中:2dr∗可通过式(48)令R1/R2=1 而确定;β0为充填角(用弧度表示),可采用给定VL∗B和θ时关于β0的隐式公式确定:
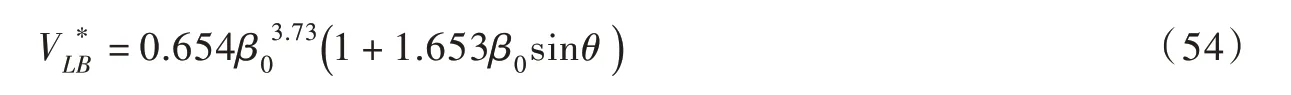
依据大体积液桥F*的Young-Laplace 方程数值解(如图10所示,VL∗B=0.13 且θ=20°)可知:F*(已采用颗粒等效半径无量纲化)与VL∗B、 2d∗、和θ有关,即如果颗粒半径(R1和R2)的影响可用Re描述,则F*应与无关。当2d∗较小时,对F*基本无影响(图10),这与文献[10]中的研究结论一致;当2d∗较大甚至液桥即将断裂时,对F*影响较为显著(图10)。进一步整理不同条件下液桥恰好断裂时Fr∗(即F∗(2d=2dr∗))与VL∗B的关系,如图11所示:当液桥体积较小时(即VL∗B≤1×10-3),对Fr∗基本无影响;当液桥体积较大时(即VL∗B>1×10-3),对Fr∗影响显著。因此,当液桥体积较小时,毛细力公式中无需考虑的影响;反之,当液桥体积较大时,则应在该公式中考虑的影响。
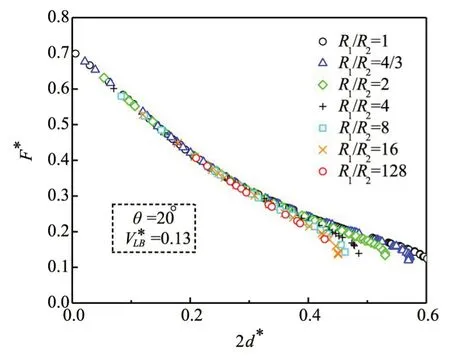
图10 R1/R2 不同时F *与2d *的关系
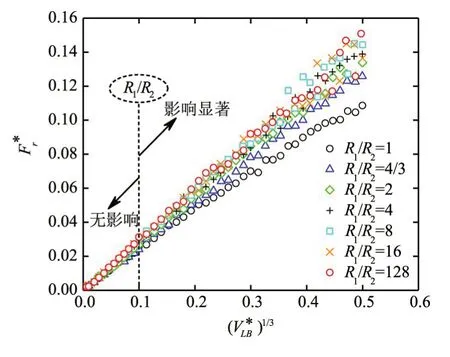
图11 R1/R2 不同时Fr *与VL*B 的关系
由此可见,式(52)(53)所示无量纲的液桥毛细力及其断裂距离拟合公式均未考虑的影响,因而Lian 等[11]的拟合公式无法精确描述不等径湿颗粒间大体积液桥的毛细力。为对比分析Wil⁃lett 等[10]和Lian 等[11]提出的毛细力拟合公式对Young-Laplace 方程数值解的预测精度,选取R1/R2=16 且θ=20°时,不同体积(VL∗B=1×10-6、1×10-3、0.03 和0.09)液桥的F*与关系的Young-La⁃place 方程数值解及这两种公式预测值作为示例,如图12所示。由图12(b)—(d)可知,当d*≤0.5dr∗、θ≤40°且1×10-3≤VL∗B≤0.13 时,Willett 公式的预测误差小于5%;然而,对比图12(a)(b)可知,当VL∗B≤1×10-3时,其预测误差超过10%。相比之下,当d*≤0.5dr∗且VL∗B≤1×10-3时,Lian 公式的预测误差小于10%。然而,这种公式对大体积液桥预测误差较大,由图12(c)(d)可知,当VL∗B=0.09 时,Lian 公式因其未考虑R1/R2的影响而对F*的Young-Laplace 方程数值解预测误差超过10%。此外,由图12(a)亦可看出:极小体积液桥(VL∗B=1×10-6)在临近断裂的过程中,相应的Young-Laplace方程数值解及不同种公式的预测值会出现不同程度的波动现象,这与3.5 节所述液桥表面(尤其在最窄“颈部”处)的自由能对其稳定性的显著影响有关,而且当液桥表面的自由能随其体积增大时,这种波动现象会消失(如图12(b)—(d)所示)。
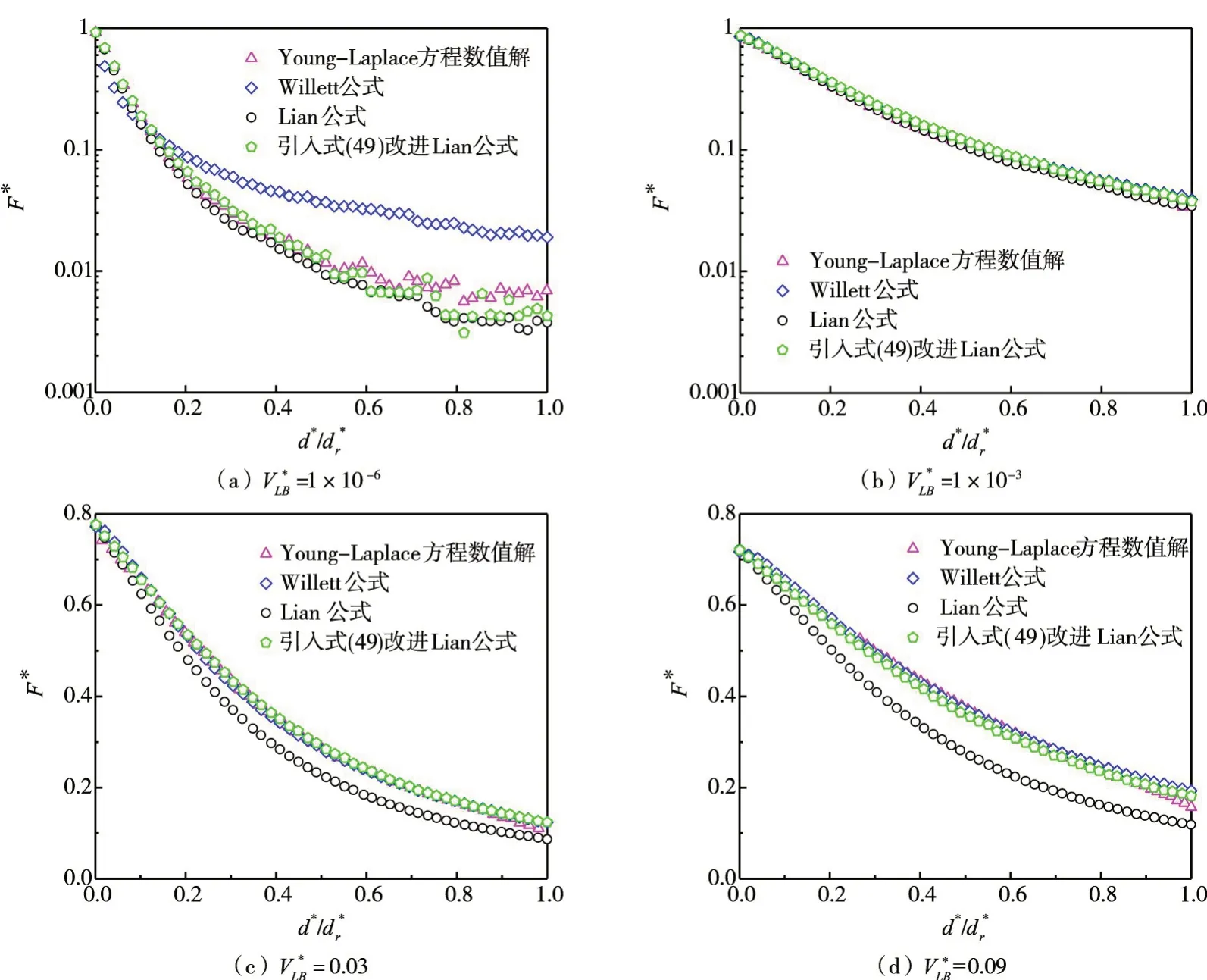
图12 VL*B 和不同时F *的Young-Laplace方程数值解与Willett公式、Lian公式及其引入式(49)的改进公式预测值(=16和θ =20°)
为提高Lian 公式的预测精度,可在式(52)所示F*公式或式(53)所示dθ公式中引入R1/R2。出于计算合理、简便考虑,采用预测无量纲液桥断裂距离更为合理的式(49)替换式(53)所示2dr∗,以考虑R1/R2的影响。由图12可知,改进的Li an 公式对小体积液桥至大体积液桥(≤0.13)的毛细力Young-Laplace 方程数值解预测均较为吻合,预测误差小于5%,优于两种已有公式。由图12(a)亦可知,不等径湿颗粒间的大体积凹形钟摆状液桥仅存于最小颗粒间距大于零范围内。当给定小颗粒-液桥接触半径yc2和液桥最窄“颈部”半径y0时,该最小颗粒间距对应2.2 节所述大颗粒-液桥接触半径yc1解存在区域的下边界。由此可见,文献[11]所述采用零颗粒间距进行变量无量纲化的方法不适用于大体积液桥(如VL∗B= 0.09)。
4.3 考虑颗粒粒径和液桥体积的毛细力计算方法应用讨论本构模型的构建是土坝变形及其稳定性计算中的关键环节。如研究背景所述,当坝前水位骤降时,构成坝体的湿颗粒材料内部的毛细黏聚作用至关重要。如文献[8]所述,要在湿颗粒材料的微细观结构弹塑性本构模型中考虑这种毛细黏聚作用,则需计算湿颗粒间的毛细力,文献[8]中虽引入了毛细力公式,但仅与颗粒间距有关,因未考虑不同体积液桥而无法考虑水位骤降引起饱和度变化对此类本构模型的影响。为此,若以颗粒级配较分散的湿颗粒材料为研究对象,将其简化为不等径湿颗粒-液桥模型,颗粒半径(R1和R2)分别取这种材料最大、最小粒径的一半,固液接触角θ≤40°,再采用等效颗粒半径Re对液桥体积VLB和颗粒间距2d进行无量纲化得到相应的无量纲变量VL∗B和2d∗,同时把液桥划分为小体积(VL∗B≤1×10-3)和大体积(1×10-3<VL∗B≤0.13)两个范围,则可将本文提出的考虑颗粒粒径和大、小体积液桥的毛细力计算公式嵌入微细观结构弹塑性本构模型中,具体可依据图13所述思路从以下4 个步骤实现:

图13 不同体积液桥断裂距离及其毛细力计算公式在微细观结构弹塑性本构模型中的应用思路
(1)当VL∗B≤1×10-(3θ≤20°)时,依据3.5 节所述将液桥断裂距离解析公式(式(46))与毛细力解析公式(式(47))相结合的思路,计算小体积液桥产生的粒间毛细力F。
(2)当1×10-3<VL∗B≤0.13 时,依据4.2 节所述引入式(49)改进Lian 等[11]的毛细力拟合公式(式(52))的思路,计算大体积液桥产生的粒间毛细力F。
(3)计算不同体积液桥在湿颗粒构成孔隙空间内所占的饱和度:依据图2所示不等径湿颗粒之间构成的孔隙空间计算孔隙体积Vv,则液桥所占的饱和度可按照下式计算:
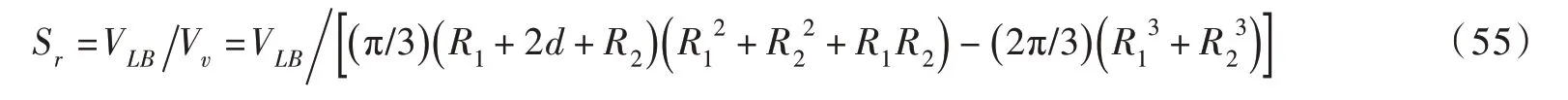
(4)将粒间毛细力嵌入微细观结构弹塑性本构模型进行土坝变形及其稳定性计算的基本思路:将第(1)、(2)步所述不同体积液桥所产生的粒间毛细力作为外荷载加入湿颗粒间的接触力中,进而将所有粒间接触力代入文献[8]所述Hertz-Mindlin 弹性接触公式和Mohr-Coulomb 屈服准则中,以分析第(3)步所计算饱和度对这种材料毛细黏聚作用的影响,进而结合非饱和土的水力特性参数(持水曲线、渗透系数函数)与有效应力张量在离散单元(DEM)程序中建立土坝在非饱和渗流作用下的数值模型,即可开展土坝在水位骤降时的变形及其稳定性计算。这也是本文下一步的研究方向。
5 结论
为研究湿颗粒间的细观毛细黏聚作用机理,开展了考虑颗粒粒径和液桥体积的毛细力计算分析,将湿颗粒简化为一对不等径球体颗粒,结合其间液桥的几何特征构建了Young-Laplace 方程数值解的数据组,一方面基于椭圆弧假定对小体积液桥推导解析公式,另一方面基于Young-Laplace 方程数值解构建适用于大体积液桥的拟合公式,主要得出以下结论:
(1)椭圆弧假定对不等径湿颗粒间的小体积液桥(VL∗B≤1×10-3)在固-液接触角θ≤20°的范围内是适用的。由该假定可知,大、小颗粒与小体积液桥的接触半径基本相同(即yc1≈yc2),并且已通过Young-Laplace 方程数值解得到验证。当液桥体积较小时,依据椭圆弧假定的解析研究和Young-Laplace 方程数值解分析表明:采用颗粒等效半径可将等径湿颗粒的解析公式推广至不等径湿颗粒的范围。基于椭圆弧假定推得液桥断裂距离及其毛细力关于液桥体积和颗粒间距的解析公式,并采用已有文献中不等径球体颗粒间小体积液桥的毛细力实测值验证了解析公式的有效性。
(2)当液桥体积较大时(VL∗B>1×10-3),由Young-Laplace 方程数值解可知:不等径湿颗粒的公式不能简单地通过在等径湿颗粒公式中采用颗粒等效半径代换得到。因此,对液桥体积变化更广范围内Young-Laplace 方程数值解的数据组进行曲线拟合,通过引入颗粒半径比构建了适用于大体积液桥(VL∗B>1×10-3)的断裂距离拟合公式。
(3)将(2)提出的断裂距离拟合公式引入已有不等径湿颗粒间液桥的毛细力拟合公式进行改进,并采用Young-Laplace 方程数值解的数据组评价了已有毛细力拟合公式的适用性,通过对比预测误差发现:改进公式对半径比在1~128 范围内的湿颗粒间不同体积液桥(VL∗B≤0.13)在固-液接触角θ≤40°且颗粒间距不超过液桥断裂距离范围内的毛细力预测效果优于已有公式。
本文提出的毛细力计算方法可嵌入典型湿颗粒材料的微细观弹塑性本构模型,旨在用于水位骤降时土坝在非饱和渗流作用下的变形分析及其稳定性评价。

