低含沙量条件下张瑞瑾挟沙力公式中参数确定及其在荆江的应用
周美蓉,夏军强,邓珊珊,刘 鑫
(武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072)
1 研究背景
水流挟沙力通常指在一定的水流及泥沙综合条件下,水流能够携带悬移质中床沙质的临界含沙量[1]。水流挟沙力公式及其参数选取的合理性,直接影响到河床冲淤变形的计算精度。目前国内外已有众多学者对水流挟沙力公式进行了深入研究,提出各类经验或半经验半理论的计算公式[2-5]。在少沙河流上,如长江中下游,通常采用张瑞瑾公式计算水流挟沙力,其结构形式简明,实际应用方便[5-8]。该公式一般可写成如下形式:

式中:k为包含量纲的系数,kg/m3;m为指数;ωm为非均匀悬沙的平均沉速,m/s。此处定义U3/ (ghωm)为水沙综合参数,并用符号C表示。
然而应用张瑞瑾挟沙力公式的实际困难在于公式中系数k和指数m的取值不易确定,两者在不同水沙条件下存在不同取值,需要根据实测资料确定。目前确定各类挟沙力公式中参数的方法主要包括两类:通过不断调试系数和指数,使得计算的含沙量过程与实测值能较好地符合[7-9];通过大量实测挟沙力资料,直接率定出公式中的系数与指数[10-11]。目前采用第二类研究方法的成果较少,如武汉水利电力学院水流挟沙力研究组[12]曾采用1956—1958年长江中下游资料(仅有1 组含沙量小于0.1 kg/m3)对张瑞瑾挟沙力公式进行率定(k≈0.0530,m≈1.54),而三峡工程运用后,悬沙含量急剧减小,且以小于0.1 kg/m3为主,故有必要增加超低含沙量数据,使率定的参数更适合三峡工程运行后的情况;方波[10]则收集了长江下游大通-镇江河道大量水文泥沙实测资料,采用|Δh/Δt|≤0.1 m/d 作为判断冲淤相对平衡的指标,选取实测水流挟沙力数据,由此率定出该河段张瑞瑾挟沙力公式中的参数(k=0.068 kg/m3,m=1.457);Xia 等[11]根据黄河下游8 个水文站的实测挟沙力资料,验证了张红武挟沙力公式中参数取值的准确性(k=2.5 kg/m3,m=0.62),该公式多用于高含沙河流。
但不同研究者通过上述两种方法确定的参数取值差异较大。余明辉等[13]采用张瑞瑾挟沙力公式时,k和m分别取为0.25 kg/m3和0.75;在郭庆超[14]和Yuan 等[8]的研究中,系数k为0.07 kg/m3,指数m为1.14;在Zhou 等[7]的模型中,k和m则分别为0.15 kg/m3和1.0。主要是由于不同研究河段与时段内的水流、泥沙等条件不同,导致参数的取值亦不同。因此,对某一长河段或同一河段的长时段模拟,若将挟沙力公式的参数取为常数,在水力泥沙要素变化较大时,数学模型难以准确地模拟水沙输移过程。故有必要根据实际的水沙条件,调整挟沙力公式的参数取值,从而提高数学模型应用于天然河流的适应能力。实际上,张瑞瑾等[1]的研究成果已表明,挟沙力公式的系数和指数随水沙综合参数C而变化,并给出了参数k,m与C之间的关系(图1)。图中曲线由许多准平衡河流实测资料和水槽试验数据率定得到(原武汉水利电力学院玻璃水槽、南京水利实验处钢板水槽、长江、黄河等)。由图1可知,当水沙综合参数C小于4.0 时,指数m为常数,约等于1.5,而当C大于4.0 时,m随其增加而减小;系数k则一直随着C的增加而增加,但在C小于10.0 且含沙量小于0.1 kg/m3的范围内,k的变化过程未给出。然而三峡工程运用后水沙综合参数C值基本小于10.0,且多年平均含沙量由工程运用前的1.0 kg/m3减小到0.1 kg/m3左右。故需重新率定低含沙量及小水沙综合参数条件下张瑞瑾公式中的系数k和指数m,以适用于近期长江中游悬沙输移计算。
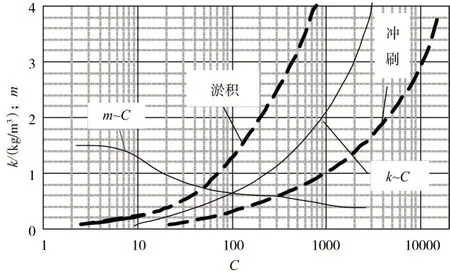
图1 挟沙力公式中参数k、m 与水沙综合参数C 之间的关系[1]
基于上述分析,本研究收集了大量实测资料,开展了长江中游河段水流挟沙力的研究,确定了低含沙量(即含沙量小于10 kg/m3)及小水沙综合参数情况下张瑞瑾挟沙力公式中参数的取值方法,并应用于长江中游荆江河段的水沙输移计算。
2 低含沙量水流挟沙力资料整理
在本次分析中,收集了长江中游河段的三组实测资料,用于研究水流挟沙力与相应水沙条件之间的关系。各测站水力泥沙要素变化范围,如表1所示。
第一组:三峡工程运用前,长江中游宜昌、陈家湾、沙市、新厂、监利、洪水港、螺山、汉口、青山(南)及青山(北)10 个水文或水位站1956—1958年各测次的水力泥沙要素,排除数据缺失或偏差较大的23 测次,共计80 组[15]。这些实测数据包括悬移质中床沙质含沙量S′(扣除冲泻质部分,0.0026 ~0.4110 kg/m3),流量Q(3720 ~70 500 m3/s),流速U(0.75 ~2.79 m/s),水深h(3.1 ~17.9 m),平均沉降速度ω′m(扣除冲泻质)等。该组数据测量时尽量保证了河床为基本冲淤平衡状态,并经过严格的审查和挑选,实测含沙量大小总体上可近似等于水流挟沙力。
第二组:三峡工程运用前,长江中游新厂站1982—1985年数据共40 测次,包括悬移质含沙量S(未扣除冲泻质部分,0.093 ~3.760 kg/m3),流速U(0.77 ~2.10 m/s),水深h(3.6 ~13.3 m),悬沙级配ΔPsk,床沙级配ΔPbk等[16]。这组数据也在河床基本冲淤平衡时测得。
第三组:三峡工程运用后,长江中游荆江段枝城、沙市和监利水文站的实测资料共453 测次,包括悬移质含沙量S(未扣除冲泻质部分,0.002 ~0.812 kg/m3),流速U(0.43 ~2.43 m/s),水深h(4.5 ~17.1 m),水位Z(23.91 ~46.18 m),悬沙级配ΔPsk,床沙级配ΔPbk等。三峡工程的运用使坝下游河段经历持续的河床冲刷,但存在某些特定时段,河床处于相对平衡状态,此时的含沙量可近似等于挟沙力。本研究判定河床是否处于相对冲淤平衡状态的标准为平均床面高程的变化率小于0.01 m/d。通过水位减去水深得到平均床面高程,则为平均河床高程的变化量,即为平均床面高程变化率。
需说明,较短时段内的河床冲淤状态不能反映其真实情况,故武汉水利电力学院水流挟沙力研究组[15]指出:需要进一步计算各测站相邻三天的冲淤变化,来确保该断面处于相对平衡状态。而在本研究中,水沙要素的测量时间不连续,无法采取上述方法进行冲淤平衡的数据审查。但此处采用的平均床面高程的变化量 |Δ(Z-h)|为一定时间间隔内的冲淤厚度,总体上可反映出较长时段内该断面处于冲淤较小的状态。经统计,收集的枝城(2003—2011)、沙市(2003—2013,2015—2016)和监利站(2003—2012,2015—2016)的数据共计3123 测次,符合判定标准的数据为561 测次。由于水位涨、落率较大的时段,河床变形一般会相对剧烈,故进一步筛选了水位变幅的数据,共计453 测次。此外,由于选取的数据为枝城、沙市等水文站的水沙资料,其所在局部河段通常要求相对顺直平整,水流集中,无整治工程,且河宽及水深等无明显纵向变化(河流流量测验规范(GB 50179-2015)),故可近似认为本研究选取的资料均接近均匀流条件,一定程度上避免了水流非恒定性带来的加速度对水位、水深等要素的影响,以及护滩护底等整治工程对床沙组成测量的影响。
然而,按照现行泥沙测量规范,一般采用五点法测量垂线平均含沙量,在距离河底0.5 m 近底范围悬沙不采样,这是目前含沙量测量广泛存在的一个问题。He 等[17]等根据长江水文局荆江局在2010年后开展的荆江段近底含沙量测量数据,发现若忽略在近底区域(距离河底10%水深范围内)的含沙量,则泥沙通量在枝城、沙市和监利站将分别被低估23.5%、9.4%和18.7%。因此,本研究计算的悬移床沙质含沙量会较实际偏小。考虑到在水沙数学模型应用中,用于率定及验证的含沙量同样未考虑近底区泥沙。若要修正含沙量来率定挟沙力公式,则在模拟中的含沙量过程也需进行相应修正,否则仍无法准确计算冲淤过程。鉴于上述情况,本文暂不进行含沙量修正,有待于后续进一步的研究。
3 张瑞瑾水流挟沙力公式参数确定
采用基于上述原则选取的相对冲淤平衡状态下的含沙量资料(可近似等于水流挟沙力),对张瑞瑾挟沙力公式进行率定,从而确定公式中的参数取值。主要计算步骤包括:悬移床沙质含沙量S′与水沙综合参数C′(扣除冲泻质部分)的计算;挟沙力公式中参数k和m与C′关系式的建立。
3.1 悬移床沙质含沙量与水沙综合参数的计算
(1)悬移床沙质含沙量S′的计算。悬移床沙质含沙量,即扣除冲泻质部分,为实际参与造床作用的含沙量S′=S-S冲泻质[15]。在具体计算中,通常将悬移质级配曲线与相应的床沙级配曲线进行对比,来划分悬移质中的床沙质与冲泻质部分[15]。具体划分原则如下:在床沙级配曲线P<10%的范围内,如出现比较明显的拐点,就取与这一拐点相应的床沙粒径作为悬移质泥沙中区分床沙质与冲泻质的临界粒径dc。曲线中拐点的出现,表明悬移质中大于此粒径的泥沙是床沙中大量存在的,应属于床沙质范围;而小于此粒径的泥沙是床沙中少有或没有的,水流中这组泥沙几乎不与床面发生交换,故属于冲泻质范畴[15]。为简化计算,通常取床沙级配曲线上P=5%对应的粒径作为临界粒径dc;然后dc在悬移质级配曲线上对应的百分比即为冲泻质所占比例,从而求出悬移床沙质的含沙量。
采用该方法计算,第一组实测资料直接给出了三峡工程运用前长江中游10 个测站的悬移床沙质含沙量S′,变化范围在0.0026 ~0.4670 kg/m3之间(表1)。第二组数据中,悬移质含沙量S则需根据上述原则扣除冲泻质部分:新厂站的床沙质和冲泻质临界粒径dc范围为0.010 ~0.104 mm;冲泻质所占比例ΔP冲为7% ~94%(平均值70%);计算得到的悬移床沙质含沙量S′范围为0.0411 ~0.8334 kg/m3。第三组资料中,枝城、沙市、监利3 站的悬移床沙质含沙量S′范围为0.0 ~0.3464 kg/m3;临界粒径dc的平均值分别为0.140、0.119、0.112 mm;且冲泻质所占比例分别介于25% ~99%(平均值82%)、18% ~96%(平均值57%)、12% ~93%(平均值47%)之间。
(2)水沙综合参数C'的计算。计算水沙综合参数时,需相应扣除冲泻质部分,记为平均沉速ω′m采用韩其为方法计算,N为挟沙力分组数,ωk为第k粒径组悬移质泥沙沉速, ΔP∗k为挟沙力级配,其值可由李义天[18]提出的方法确定。由于m是待确定量,故根据以往的研究成果将其分别取为0.5、1.0 及1.5,计算得到第三组的C′(453 测次)分别在0.024 ~13.775、0.024 ~12.253 及0.023 ~11.023 范围内。可见,随着m取值的增大,ω′m增大,C′ 相应减小,但变幅不大,平均相对差值(MRE1.5-0.5)为9%。故此处将m取为1.0 进行平均沉速的计算。总体上,长江中游的水沙综合参数C′在10.0 以内(表1),且其值在不同时段或不同位置差异较大。
3.2 挟沙力公式参数与水沙综合参数的关系建立此处首先分析悬移质总含沙量S与水沙综合参数C(不扣除冲泻质)的关系,以此解释选取水流挟沙力数据时需要扣除冲泻质部分的原因;然后进一步研究悬移床沙质含沙量S′与水沙综合参数C′的关系;在此基础上确定张瑞瑾水流挟沙力公式中参数k、m的计算关系。
(1)悬移质含沙量S与水沙综合参数C的关系。在河床处于相对冲淤平衡状态且水流与河床中各组分泥沙充分交换时,认为选取的悬移质总含沙量S(不扣除冲泻质部分)即为水流挟沙力,那么挟沙力级配近似等于悬移质级配,则根据悬移质级配计算得到平均沉速ωm,进而求得水沙综合参数C。首先,点绘悬移质总含沙量S与C的关系,如图2(a)所示。总体上,数据点较为分散,拟合的幂函数关系的决定系数较低(R2=0.55);此外,三峡工程运用后枝城和沙市站数据点与运用前两站的数据点相比,更为散乱。主要是由于这里选取的河床冲淤幅度较小时的含沙量,是水流的实际挟沙力而不是理论挟沙力。水流的理论挟沙力为泥沙供应充足情况下的水流挟沙力,该值仅由水流条件决定;实际挟沙力为在冲刷时河床补给受限条件下,水流实际能挟带的含沙量,包括冲泻质和床沙质部分;有效挟沙力则为真正参与造床作用的泥沙含量,为悬移质中的床沙质部分。此处在计算水沙综合参数C时,假设了挟沙水流与河床中各组分泥沙是充分交换的,但实际上冲泻质泥沙无法从河床获得补给,一直处于次饱和状态,故选取冲淤平衡时的含沙量小于理论的水流挟沙力。

图2 三峡工程运行前后长江中游水流挟沙力与水沙综合参数的关系
由图2(a)也可看出,枝城、沙市站的数据点较为散乱且偏低,主要是由于这两站水流中冲泻质所占比例较大,实际挟沙力小于理论挟沙力。而三峡工程运用前各站和运行后监利站的床沙组成较细,挟沙水流中冲泻质所占比例相对较小,故数据点较为集中。基于上述分析,选取含沙量和计算ωm时应当扣除冲泻质部分,即仅考虑真正与床沙进行交换且使河床处于相对冲淤平衡状态的泥沙(悬移质中的床沙质部分)。这样便可排除计算ωm时考虑了冲泻质,但实际上冲泻质无法从河床得到补给而产生的误差。上述即为计算水流挟沙力时要扣除冲泻质部分的原因。
(2)悬移床沙质含沙量S′与水沙综合参数C′的关系。通过上述分析可知,水流的有效挟沙力不仅取决于水流条件、悬沙级配,还受河床边界条件(床沙组成)影响。河床边界条件对水流挟沙力的影响,主要体现在对挟沙力级配ΔP∗k的确定上。此处采用李义天方法[18]计算挟沙力级配,具体公式可写为:

式中:ΔPbk为床沙级配;βk为与摩阻流速、 ΔPbk及ωk等相关的一个修正参数。采用式(2)计算挟沙力级配时,即认为不考虑悬移质中的冲泻质部分(ΔPbk在冲泻质范畴内均为0),故冲泻质部分的水流挟沙力为0(S∗k =S∗⋅ΔP∗k)。而悬移质含沙量S包含了冲泻质和床沙质,故需将冲泻质扣除;并根据计算的挟沙力级配,计算平均沉速ω′m。
此处点绘了三峡工程运用前后长江中游悬移床沙质含沙量S′与水沙综合参数C′的关系(图2(b)),可发现幂函数拟合曲线的决定系数(R2=0.76),较图2(a)(R2=0.55)有显著提高。直线斜率即为挟沙力公式的指数m≈1.5855,而通过拟合曲线与坐标轴的交点则可求出系数k≈0.0454。这些结果较为合理,大致符合图1的取值范围。从时间尺度上看,三峡工程运用前,荆江段的有效水流挟沙力在0.0026 ~0.8334 kg/m3之间;而三峡工程运用后,S′则分布在0.0 ~0.3464 kg/m3之间,水流有效挟沙力总体上有所减小。从空间尺度上看,三峡工程运用后,有效水流挟沙力沿程递增(S′枝城<S′沙市<S′监利)。究其原因,主要是由于S′反映的是水流中有造床作用的床沙质部分的挟沙力,三峡工程的运用使得河床发生粗化且越靠近大坝粗化程度越高,从而导致冲泻质临界粒径沿程增大,水流中床沙质部分挟沙力相应减小。
(3)挟沙力公式参数k和m计算关系的确定。从图2(b)的点绘结果可看出,数据点的分布并非完全符合幂函数关系(直线),其变化趋势总体呈现为斜率变小的曲线。故首先将S′ 与C′ 取对数,并进行数据点平移,变形为lgS′+a和lgC′+b,旨在使两个值均大于0;再在直角坐标系中进行拟合,并取最优拟合方式;然后,求拟合曲线的斜率,即为不同水沙综合参数C′ 下对应的m值,并进一步得到k值;最后,绘制k、m与C′ 的关系图,并采用不同函数进行分段拟合,取最优拟合结果。根据上述方法,即可建立张瑞瑾挟沙力公式中参数k和m与C′ 之间的计算关系。此处a、b暂取为5 和2,首先采用各种函数形式进行拟合,最终以对数拟合为优(图3),得到的关系式为1gS′+5=2.3097×ln(lgC′+2)+2.0641,并进一步计算得到各水沙综合参数C′ 对应的k和m值。

图3 三峡工程运用前后长江中游水流挟沙力(lgS ′+5)与水沙综合参数(lgC ′+2)的关系
然后将数据点k、m与C′进行分段拟合,使符合度达到最高(图4),则不同C′范围内k、m的拟合曲线可分别表示为:
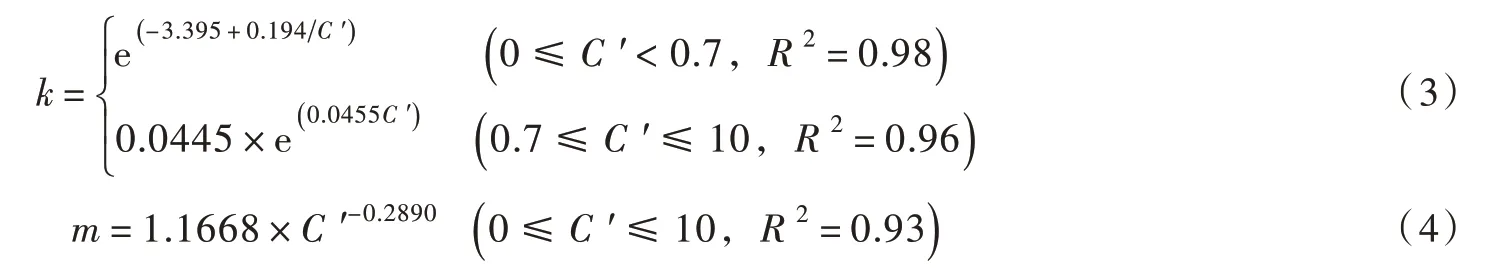
在长江中游河段,水沙综合参数C′基本小于10.0,故获得该范围内k、m的取值基本适用。当C′>10.0 时,其值可由张瑞瑾等[1]确定的关系曲线决定(图1)。由图4可知,系数k随C′先减小后增大,当0.2≤C′ <0.7 时,k由0.088 减小到0.044 kg/m3;而当0.7≤C′ ≤10.0 时,k有逐渐增大趋势,由0.046 增加至0.070 kg/m3。指数m随C′的增大而减小,当0.2≤C′≤10 时,m由1.86 减小至0.60。基于上述式(3)和式(4),则可根据C′确定k、m值。

图4 k、m 随水沙综合参数C ′的变化过程
此处采用长江中游各测站的低含沙量实测数据,确定了张瑞瑾水流挟沙力公式中参数k、m的计算关系,这些计算关系适用于低含沙水流及小的综合水沙参数C′。该方法弥补了以往在低含沙条件下难以确定张瑞瑾挟沙力公式中参数的不足。但应当指出,这些计算关系仅适用于长江中游,在其他低含沙水流上不一定适用。由于水流的有效挟沙力与水沙及河床边界条件均相关。故在不同的河流上,挟沙力公式的参数取值将有所不同。例如,韩其为挟沙力公式[19]中系数k取为0.245,偏大于本文k值,主要是由于其在公式率定时采用了长江、黄河、丹江口水库等多条河流的资料,数据点范围相对较广,实际针对长江的k值应显著小于黄河上的值。然而,在边界条件大致相同的情况下,这些计算关系仍具有参考价值。
4 张瑞瑾水流挟沙力公式计算实例对比
此处将张瑞瑾挟沙力公式中参数的计算式(3)和式(4),嵌入到已有的一维水沙数学模型中,进一步验证该公式的准确性及适用性。该一维模型的水沙控制方程及数值解法,详见文献[20]。首先,按以往常规方法,将参数k和m取为常数,模拟了2016年荆江段(枝城至城陵矶)的水沙输移过程;然后,由计算式确定参数k和m,再次模拟了该年荆江段水沙输移过程;最后,比较了不同参数取值方法对模拟结果的影响。需说明,若研究河段受大规模护岸、护滩工程的守护而冲刷受限,可在模拟中通过修正挟沙力的方法来考虑这一影响[20]。
4.1 荆江河段概况荆江河段位于长江中游,上起枝城(荆3),下至城陵矶(荆186),全长347 km(图5)。干流的水沙主要来自上游,其间通过松滋口、太平口、藕池口分流入洞庭湖,又于城陵矶处重新汇入长江干流。如忽略三口(松滋口、太平口及藕池口)分流的影响,枝城站可以作为控制断面,则该站实测水沙过程代表进入整个荆江段的水沙条件。三峡工程运用前(1994—2002年),枝城站年均水量为4304 亿m3/a,而年均输沙量为3.74 亿t/a。工程运用后(2002—2017年),受人类活动及气候变化的影响,枝城站年均水量减小到3952 亿m3/a,为蓄水前的92%;受上游水土保持工程及三峡水库拦沙作用的影响,枝城站年均输沙量大幅减小到0.43亿t/a,降幅高达88%[21]。此外,枝城站年均含沙量由工程运用前的0.869 kg/m3减小到运行后的0.109 kg/m3。三峡水库的蓄水拦沙作用使得坝下游河床发生持续冲刷,2002—2017年荆江段平滩河槽累计冲刷量达10.51 亿m3,单位河长的年均冲刷量为20.18 万(m3/(a/km)),远大于蓄水前(1975—2002年)的3.18 万(m3/(a/km))[21]。
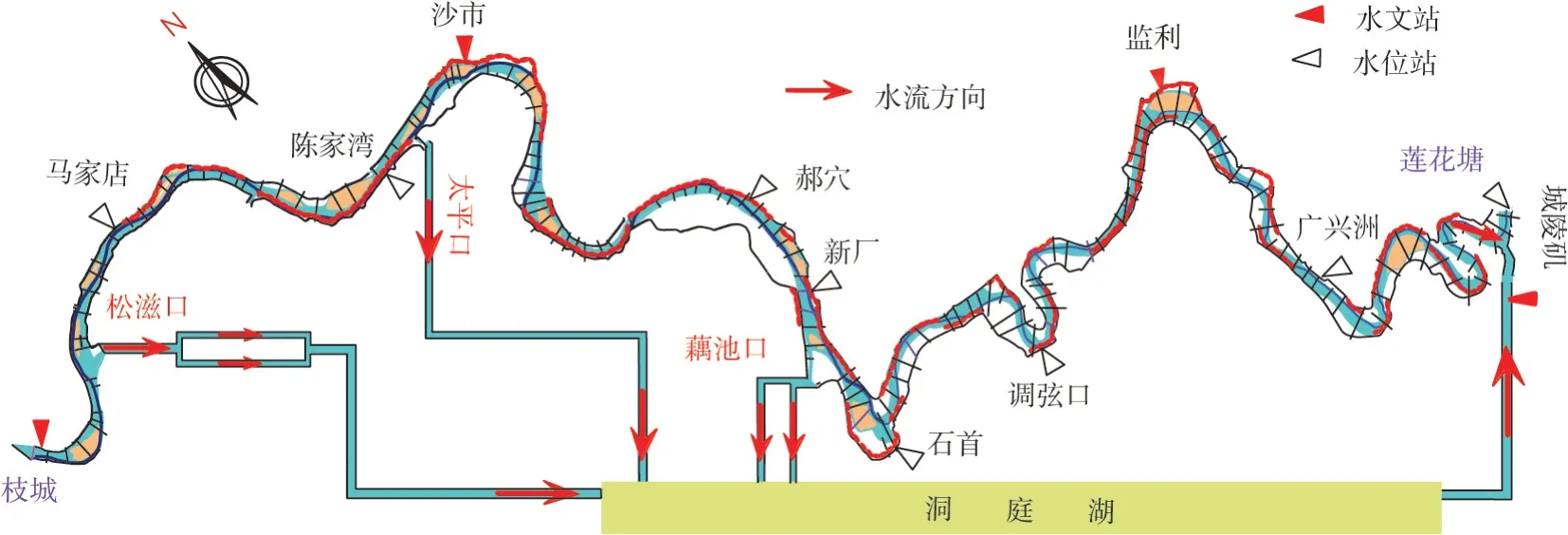
图5 荆江河段示意图
在模型计算中,以枝城站日均的流量、含沙量和悬沙级配资料作为上游边界条件;同时采用莲花塘站的日均水位过程作为下游边界条件;还需将三口分流的日均流量、含沙量和悬沙级配作为侧向边界条件。2016年枝城站最小、最大和平均流量分别为6950、34 000 和14 000 m3/s,且最小、最大和平均含沙量为0.003、0.147 及0.016 kg/m3;在莲花塘站,水位在18.70~32.32 m 之间变化(图6)。另外,采用荆江段173 个汛后实测固定断面地形和72 个固定断面的实测床沙级配(施测时间为2015年10月)作为初始河床边界条件,其中床沙的中值粒径范围为0.17 ~0.33 mm;其余断面的初始级配由这些实测值插值求得。由于在长江中游河段,推移质输沙量仅占悬移质输沙量的1%~2%[21-22],对河床变形的影响很小,故在冲淤计算中未考虑推移质输移的影响。
4.2 k 和m 取常数时的计算结果分析荆江段2016年1月1日至12月31日模拟得到的各水文或水位站流量、水位过程与实测值十分吻合。在沙市站,实测最小、最大和平均流量分别为6030、28 600和12 610 m3/s,而相应的计算值为6984、27 921 和12 802 m3/s;在监利站,计算与实测的流量过程也几乎一致,平均流量的相对误差为3.9%。对于水位变化过程,在枝城、马家店等水文或水位站计算与实测水位的平均相对误差在0 ~1%之间。对于泥沙输移计算,经试算后确定当张瑞瑾挟沙力公式参数k=0.05,m=1.55 时,计算得到的2016年荆江沙市及监利站含沙量过程与实测过程符合相对较好,如图7所示。沙市站最小、最大和平均含沙量实测值分别为0.011、0.328 和0.036 kg/m3,而相应的计算含沙量为0.020、0.198 和0.039 kg/m3,且计算与实测含沙量的平均相对误差(MRE)为49%;而在监利站,计算与实测含沙量的平均相对误差(MRE)为39%。此外,监利站泥沙输移情况较为特殊。2016年枝城、沙市及监利站水位过程线的形状基本一致;而对于含沙量,枝城站的含沙量过程线呈现枯水期小,汛期陡增的双峰形状(图6),通常情况下,沙市及监利站的含沙量过程应与枝城站含沙量的变化趋势一致,但2016年监利站的含沙量在枯水期仍较大,且波动剧烈。这是由于监利站的水力泥沙条件受洞庭湖出流顶托的影响显著,含沙量变化较为复杂,故含沙量过程的模拟精度相对较低(图7(b))。

图7 2016年荆江段典型断面含沙量计算与实测过程对比(k 和m 取常数)
4.3 k 和m 由公式确定时的计算结果分析此处将挟沙力公式的参数计算式,嵌入到了一维水沙数学模型中,使模型能根据各时刻计算得到的综合水沙参数C' ,来确定参数k和m,从而求得各时刻的水流挟沙力。在此基础上,重新模拟了2016年荆江段的水沙输移过程。可知,沙市和监利站计算与实测流量的平均相对误差范围为3% ~4%;而枝城、沙市及监利站计算与实测水位的平均相对误差均在0~1%之间(图8)。因此,张瑞瑾挟沙力公式的参数取值采用不同方法时,对流量及水位计算结果的影响不大。然而沙市及监利站计算与实测含沙量的平均相对误差分别减小至26%和36%(图9)。经比较,计算含沙量与实测值的符合度较k和m取常数时基本一致或有所提高。因此,张瑞瑾挟沙力公式的参数取值采用公式计算时,能根据水力泥沙要素自动调整,对天然河流的适应性更强,且含沙量过程的模拟也更为准确。但总体上看,含沙量的计算和实测值误差仍较大,尤其在监利站,主要是因为该站的含沙量过程较为复杂,其较大程度上受到下游洞庭湖水沙入汇的影响,仅根据现有的一维水沙数学模型无法考虑这一影响。

图8 2016年荆江段典型断面水位计算与实测过程对比
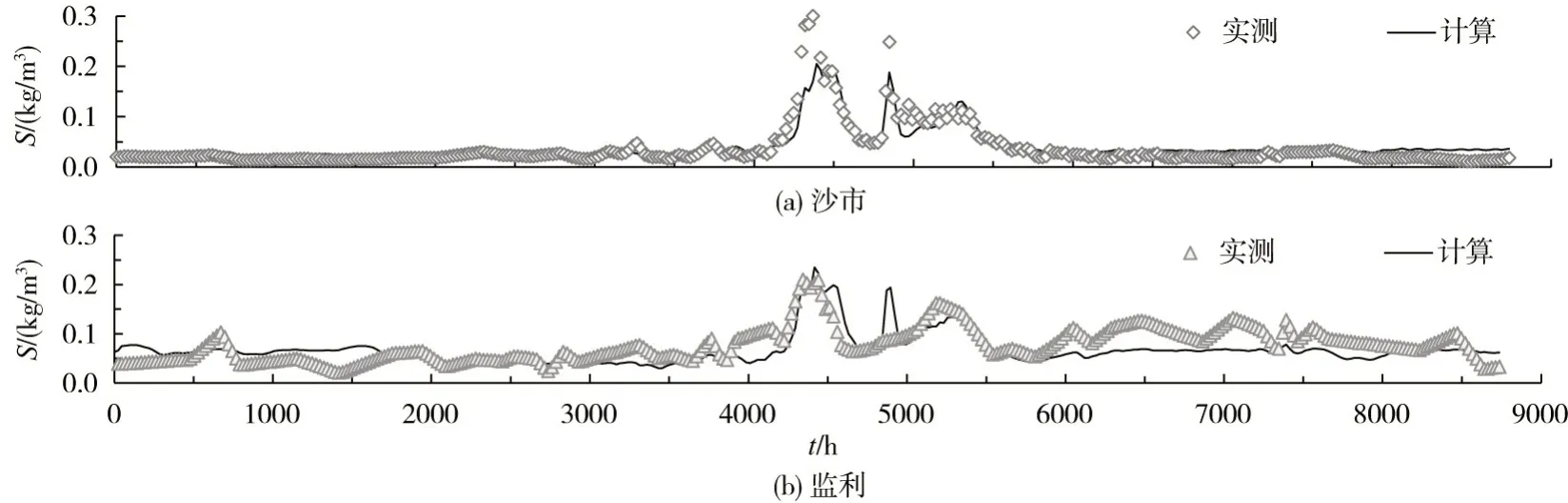
图9 2016年荆江段含沙量过程计算与实测结果对比(k 和m 由公式决定)
分析2016年沙市、监利站计算得到的综合参数C′,其值范围为0.26 ~0.89 和0.38 ~4.78。在这范围内,k的取值变幅不大,分别在0.044 ~0.070 kg/m3(平均值为0.052 kg/m3)和0.045~0.056 kg/m3(平均值为0.048 kg/m3)之间;而m变化较为显著,范围分别为1.21 ~1.72(平均值为1.46)和0.74 ~1.55(平均值为1.05)。通过比较,沙市站和监利站的综合水沙条件存在一定的差异,使得相应的k和m取值也存在一定的差别。
5 结论
本研究基于长江中游的实测水沙资料,确定了低含沙量情况下张瑞瑾挟沙力公式中系数和指数的计算关系。并将该参数计算式嵌入到一维水沙动力学模型中,进一步验证公式的准确性及适用性。本研究得到如下主要结论:
(1)选取三峡工程运行前、后相对冲淤平衡状态下的水流含沙量(除去冲泻质部分)共计573组,将其近似等于水流挟沙力,并点绘水流挟沙力和综合参数关系,从而确定参数k和m计算式。结果表明:系数k随C′的增大呈现先减小后增大的趋势,当0.2≤C′<0.7 时,其值由0.088 减小到0.044 kg/m3;而当0.7≤C′ ≤10.0 时,该值由0.046 增加至0.070 kg/m3。指数m随C′的增大而减小,在0.2≤C′≤10 范围内其值由1.86 减小至0.60。该参数计算式适用于低含沙水流及小的综合水沙参数条件,弥补了以往在低含沙量条件下难以确定张瑞瑾挟沙力公式中参数的不足。
(2)将参数计算式应用到一维水沙动力学模型中,并采用长江中游荆江段2016年的实测资料,对模型进行验证。结果表明:当水流挟沙力公式的参数取为常数时,各水文站计算和实测含沙量平均相对误差在39%~49%之间;而参数采用计算式确定时,含沙量平均相对误差范围为26%~36%。故挟沙力公式参数采用计算式确定时,相较于取为常数,模型能根据水力泥沙要素自动调整,对天然河流的适应性更强,含沙量过程的模拟也更为准确。

